对一道清华测试题的探究、变式及反思总结

刘海涛

(安徽省芜湖市第一中学 241000)

《中国高考评价体系》指出：高考要求学生能够触类旁通、融会贯通，既包括同一层面、横向的交互融合，也包括不同层面之间、纵向的融会贯通.高考要从“知识立意”转向“能力立意”，考查学生的“关键能力”和“核心素养”.这就要求学生在学习中，学会灵活运用所学知识分析、解决问题，达到从“解题”向“解决问题”的转变，对于一些典型问题，能够从不同角度思考，寻求不同的解法，以一题多解的方式寻求知识间的内在联系，构建知识的网络体系，加深对问题的本质认识，从而拓宽解题视野，发散解题思维，提升学习兴趣，提高解题能力.在清华大学2021年11月举办的中学生标准学术能力测试中，有一道二元分式函数最值问题，笔者结合学生的作答情况整理成文，现与读者分享交流，以期抛砖引玉.

1 试题呈现与分析

分析该题形式上以圆的方程(二元二次方程)为背景命题，主要考查分析、解决二元二次问题的能力，强化对转化与化归、函数与方程、消元与不等式求最值等数学思想方法的考查，体现了逻辑推理、数学运算、直观抽象等数学核心素养.试题结构虽简单、明了，但内涵丰富，值得研究，以发挥该题的最大价值.

2 解法探究

角度1分式齐次化，比值换元,化二次函数为一次函数.

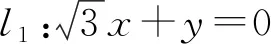
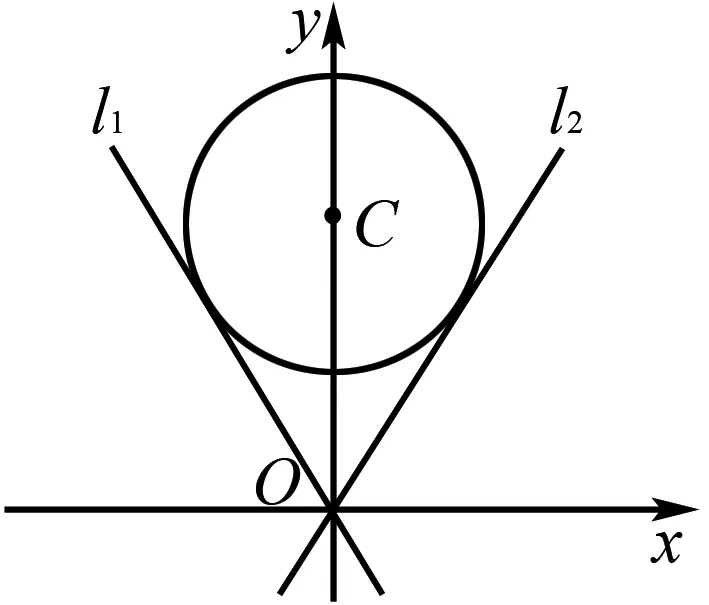
图1

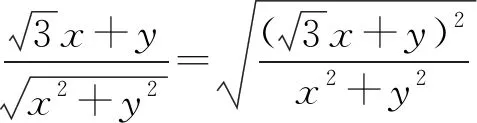
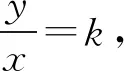
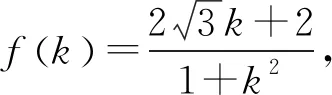
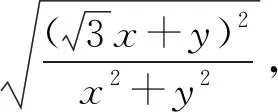
角度2联想点到直线距离和两点间距离公式，转化为直角三角形内角的正弦值问题.

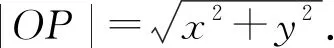
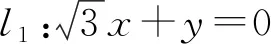
图2

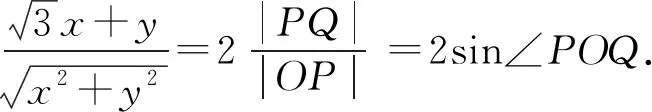
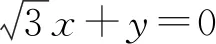
角度3联想点到直线距离公式，转化为距离问题.

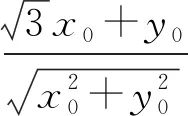
图3

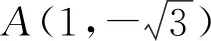
角度4联想向量夹角余弦公式，转化为余弦函数问题.

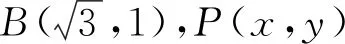
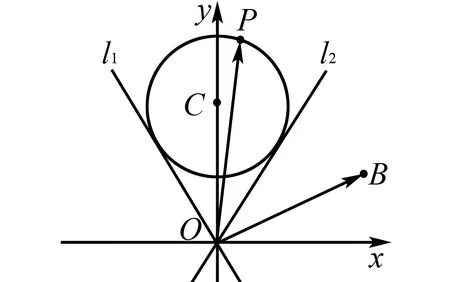
图4

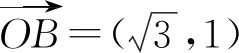
角度5联想三角函数定义，转化为三角函数问题.

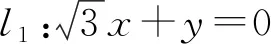
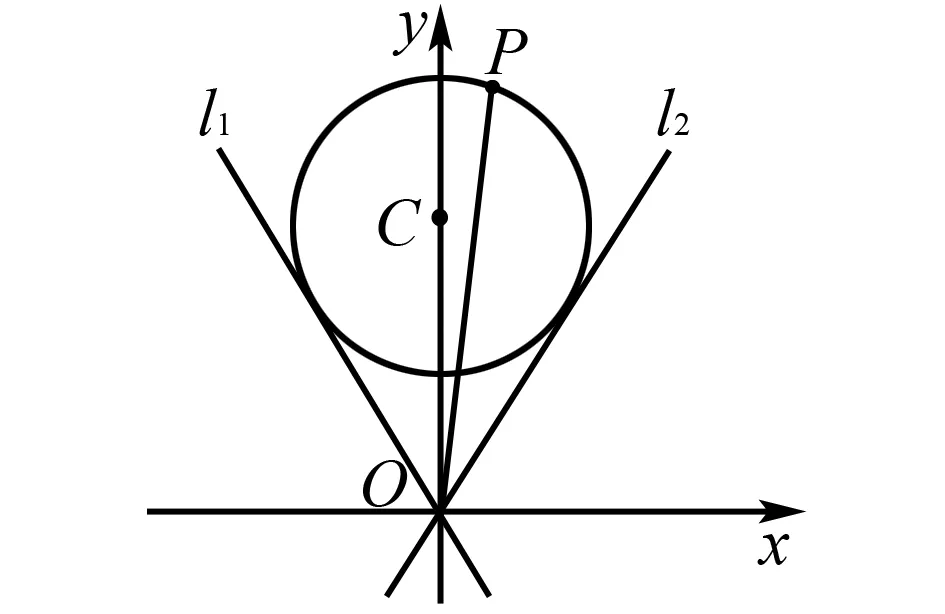
图5

根据三角函数的定义，有

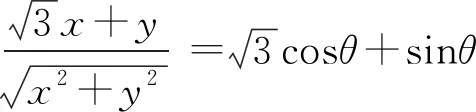
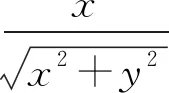
角度6极坐标换元，转化为三角函数问题.

解法6如图5，以坐标原点为极点，x轴非负半轴为极轴建立极坐标系，设P(ρ,θ)为圆C上一点，则θ∈[60°,120°].

评注极坐标换元法是解决二次函数问题的常用解法，文[3]对极坐标换元在二元函数问题中的应用做了详细的介绍，读者可以参考.

3 变式训练

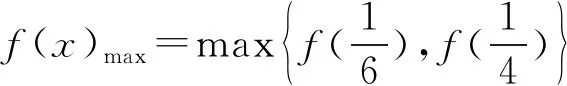
上述计算分析表明，高架桥、地铁站同期同位分离式合建结构在静力工况下安全可靠。为分析其抗震性能，采用MIDAS大型岩土隧道有限元软件GTS建立三维有限元模型(见图9)，进行抗震动力时程计算分析。

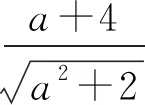
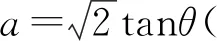
=3sin(θ+φ),

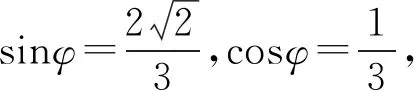
由φ≤θ+φ≤θ0+φ，

sin(θ0+φ)=sinθ0cosφ+cosθ0sinφ

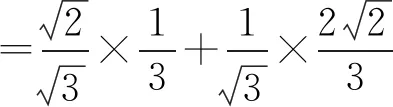
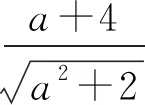
解法3(利用导数判断单调性法)

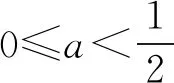
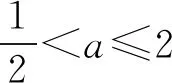
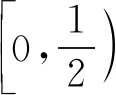
所以g(a)min=min{g(0),g(2)}

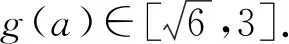
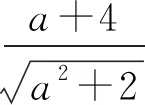
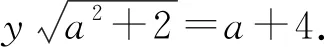
即(y2-1)a2-8a+2y2-16=0.

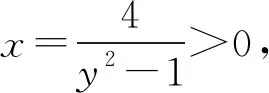
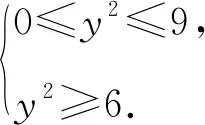
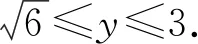
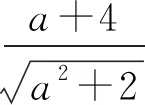
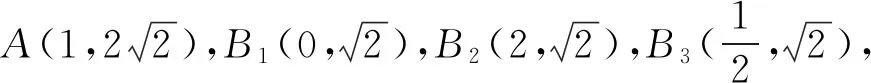
图6

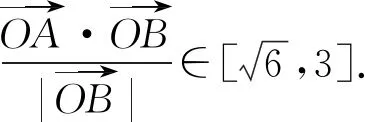
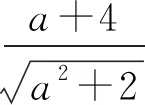
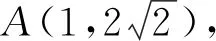
由于0≤a≤2，

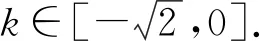
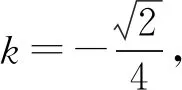
图7

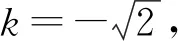
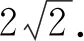
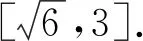
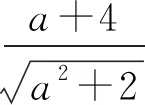
4 反思总结

4.1 一题多解，提高解题能力

数学离不开解题，数学研究的过程就是解决问题的过程，掌握数学的一个重要标志就是善于解题.可见，解题是一名教者的必备技能，技能的形成并非一朝一夕，而在于日积月累.数学解题是巩固基础知识、落实基本技能、感悟思想方法、提升思维敏锐度的系统活动，所以对一道典型问题进行多角度的分析与解答是非常必要的.笔者从六个角度对一道清华测试题予以分析，给出六种不同的解法，解法1是在观察出分式的齐次化特征后，比值换元为一次函数，再以导数为工具求函数最值.解法2至5是基于函数式的结构特征，联想所学的基本概念、公式，构造出函数式的几何意义解题，其中解法2和3联想点到直线的距离公式，分别将函数式转化为直角三角形内角的正弦值问题和距离问题；解法4联想向量夹角余弦公式，转化为余弦函数问题；解法5联想三角函数定义，转化为三角函数问题.解法6通过极坐标换元法，同样将问题转化为三角函数问题，与解法5异曲同工.用多种方法解答同一道数学题，不仅能更牢固地掌握相关的数学知识，还能更灵活地运用所学知识，加强对数学整体性的理解与认识．通过一题多解，分析、比较各种解法，可以找到最佳的解题途径，从而发散学生的思维能力，对巩固数学知识和提高解题能力大有裨益．

4.2 夯实基本知识，强化通性通法

《普通高中数学课程标准(2017年版)》指出：在数学高考命题中，考查内容应围绕数学内容主线，聚焦学生对重要数学概念、性质、方法的理解和应用，强调基础性；注重数学本质和通性通法.因此，笔者认为在日常的解题教学中，教师应加强基础知识、基本技能和基本数学思想方法的训练，以提高学生解题的基本活动经验.我们寻求一题多解，但不能满足于一题多解，更不能为了一题多解而多解，而是要在解答的过程中总结出哪种方法适合哪类题型，选择哪个方法更加合理、高效，对于一些常考题型，甚至于必考题型，教师要指导学生总结该类问题的“通性通法”，形成解题模型.通过文中对问题的多种解法不难看出，六种解法间的计算量和思维深度都有差别，但也都是解决类似分式函数的通法，那如何进行“通性通法”的训练呢？笔者认为，所谓“通性通法”一定是建立在对问题形式、结构、特征等有着深刻理解的基础之上，在有多种方法选择的情况下，能快速找到最合理、高效的方法来完成解答.在日常的解题教学中，教师要指导学生分析每一种解法的优与劣，打破总是求导判断单调性的类似经验解题的惯性思维，如解法1就是最常规解法，虽思路顺畅，但过程冗长、计算量大；解法2至5根据函数式结构特征，联想点到直线距离公式、向量数量积、三角函数定义式、数形结合解出题目；解法6直接极坐标换元，转化为三角函数问题，直接了当，干净利落.因此，教师在解题教学中要指导学生如何根据问题特征，设计最合适的算理，选择最佳的解法，这样在平常的考试及最终的高考中才能“以不变应万变”，顺利完成考试.