通过一道试题研究一类问题

李昌成

(新疆乌鲁木齐市第八中学 830002)

1 题目呈现

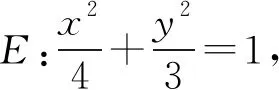
2 考生的困惑

本题中切线PA,PB的斜率未知，点P(3,t)还含有一个参数，考虑到A,B两点还要引入4个变量，解题过程中会出现7个变量，根本无法建立直线AB的方程，更不可能求解定点，思维受阻，解答搁浅.为了节省时间，减少隐性失分，学生只能以蒙了事.

3 分析问题

4 题目解答

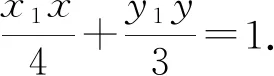
①

将P(3,t)代入①，得

②

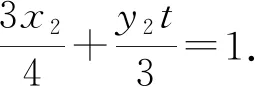
③

所以A(x1,y1)满足方程②，

B(x2,y2)满足方程③，

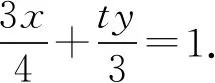
整理，得4yt+9x-12=0恒成立.

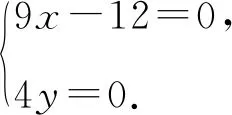
评注通过同构处理，有效避开了多个参数对解题的影响.进一步思考发现，本问题与圆锥曲线类型无关，其他圆锥曲线也可以同理作切线，问题的出口可以是长度问题、面积问题、角度问题，但本质都是要通过同构法求得含参数的直线方程，当然参数设定也可以多种多样，最终求得定点，依托定点解决最值问题或角度问题.

5 变式升华

5.1 变换曲线背景

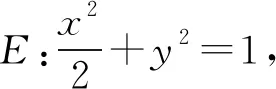
参考答案(1,0).

评注新的椭圆背景只是系数变化，对问题没有本质影响，俗称换汤不换药！

参考答案(4,0).

评注双曲线与椭圆的标准方程中虽有“±”之分，但在本类问题中，没有实质性的作用，用上述方法均可针对定点问题作答.

变式3已知抛物线E：x2=4y，过点P(t,-1)作抛物线E的切线PA，PB，切点分别是A，B，直线AB过定点____.

参考答案(0，1).

评注抛物线与椭圆的标准方程存在有无一次项之分，但已知切点写切线方程不受变量次数影响，所以依然可以用上述方法求定点.

变式4已知圆C：x2+y2=1，过点P(2,t)作圆C的切线PA，PB，切点分别是A，B，直线AB过定点____.

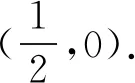
评注圆与椭圆的标准方程只是系数不同，但已知切点写切线方程不受变量系数影响，所以用上述方法求定点是没有任何问题的.事实上，圆、椭圆、双曲线、抛物线等二次曲线提供了切点法写切线的可能，已知动点的参数为切点连线过定点提供了必备条件.

5.2 变换题目出口

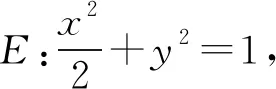
①

将P(2,t)代入①，得x1+ty1=1.

②

同理，x2+ty2=1.

③

由 ②③得直线AB的方程为x+ty=1.

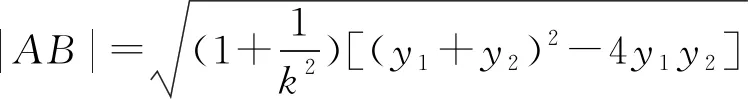
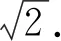
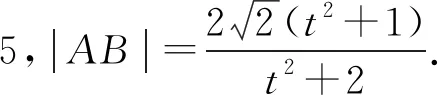
设焦点F到直线AB的距离为d，那么

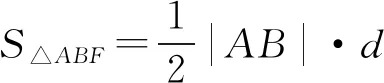
④

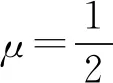
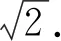
评注变式5,6分别从一维、二维角度设置问题，但问题都归结为关于t的函数，从能力考查来看，没有区别.另外，④处还可以利用基本不等式处理，有兴趣的同仁可以试一试.

解析设A(x1,y1) ，B(x2,y2)，那么PA的方程可以表示为x1x=2(y1+y).

即x1x-2y1-2y=0.

⑤

将P(t,-1)代入⑤,得tx1-2y1+2=0.

⑥

同理，tx2-2y2+2=0.

⑦

由⑥⑦得直线AB的方程为tx-2y+2=0.

所以直线AB过定点(0,1)，此点为该抛物线的焦点！

所以x1x2=-p2=-4.

⑧

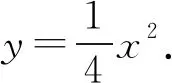
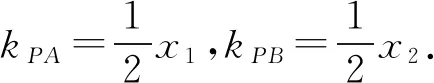
评注⑧是抛物线焦点弦的一个常用性质，因此证明直线AB过已知抛物线的焦点(0,1)十分重要.开口向上或向下的抛物线是二次函数，用导数解决切线问题是一个常用技巧.

5.3 变换参数设置方式

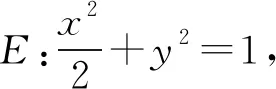
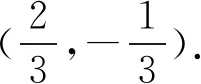
评注设P(x0,y0)，那么y0=x0-3，进而有P(x0,x0-3).这里x0的功能就是原题中t的功能.直线仅仅是提供参数的一种方式，没有其它作用，但容易迷惑学生，增加试题的区分度.

通过以上研究，我们发现圆锥曲线的这类相交切线的切点连线必过定点，用同构法求解虽然不易理解，但是运算简捷、思路清晰、操作方便，为求弦长、求面积、求夹角等问题铺平了道路，是一个优秀的通解通法.