巧用等和线解决向量双变量问题

代赵玉 许志城 魏俊潮

(1.江苏省扬州大学数学科学学院 225002；2.江苏省泰州中学数学教研室 225300)

在解决两个向量的系数之和、线性关系式与最值(取值范围)问题时，利用向量等和线求解比常规方法更显优势.此类问题的源头可以追溯到教材向量部分的例习题编写，基于此，研究者们开展一系列探索与研究.吴莉娜(2021年)从人教版和苏教版例习题出发，通过一系列变式问题层层深入探究，发现利用等和线结论可以巧妙地将复杂的求值、最值等一系列代数和问题转化为几何图形问题，将具体的代数式运算转化为距离的长度比例问题.杨瑞强(2022年)通过对普通高中教科书《数学》必修第二册第26页例1的深入探究与扩展，给出“等和线”的概念和重要性质，同时分类阐述利用“等和线”法解决几类常见的平面向量线性运算的系数和(线性关系式)、最值(取值范围)等题型，并指出了解题的关键步骤.杨德扬(2020年)、张玉虎(2019年)则主要研究等和线在求解系数和这一类问题中的应用，展现了等和线应用的简洁与高效.

1 追本溯源——等和线定理

1.1 三点共线定理

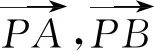
1.2 等和线

2 等和线定理的应用

2.1 拨云见日——求两变量的系数和

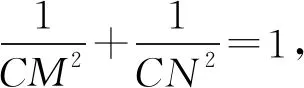
图1 图2 图3

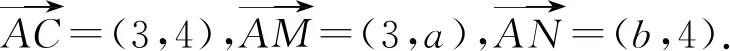
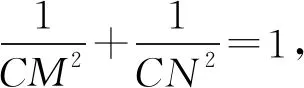
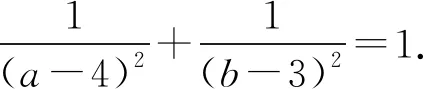
再将a,b的值代入化简，得

现假设有x+y=m，则x=y-m.

代入上式化简,得

25y2-18my+9m2-144(m-1)2=0.

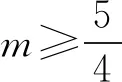
解法2 (等和线法)如图3，连接MN与AC交于点E，AC=5.

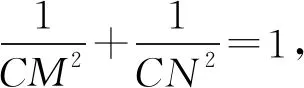
CM2+CN2=CM2·CN2=MN2.

即CM·CN=MN.

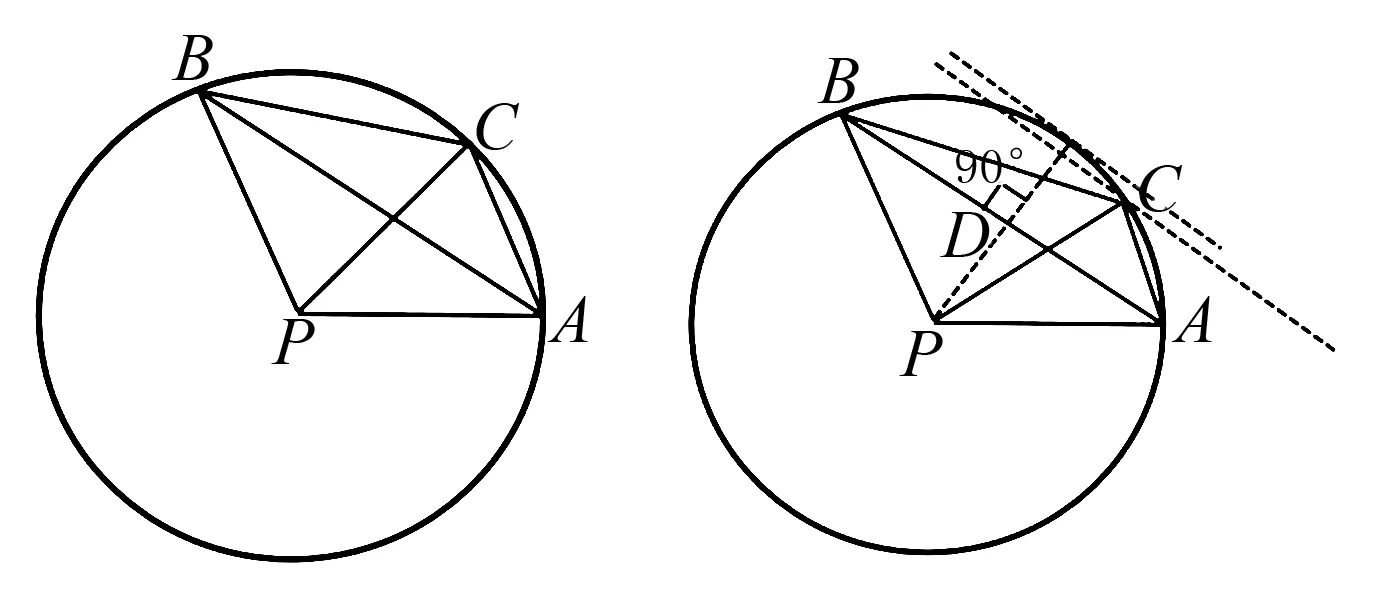
图4 图5

解法1 (常规解法)因为∠ACB=120°，所以∠APB=120°.

即有1=m2+n2-mn.

令m+n=t(t>1)，将上式化简,得

(m+n)2-3mn-1=0.

安保系统实现故障降速、故障停车和紧急停车功能。出于安全性考虑，系统中安保控制模块与其他模块的通信主要通过双冗余CAN网络实现，同时重要的安保输出(故障降速、故障停车)通过硬线连接作为备份。

即t≥2或t≤-2.则m+n最小值为2.

解法2 (等和线法)如图5，过点P作线段AB的垂线，并与AB交于点D.

因为∠ACB=120°，所以∠APB=120°.

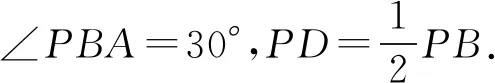
由等和线定理，得

因为PD是定值,则当PC⊥AB(PC=PB)时,m+n最小值为2.

2.2 延伸扩展——求两变量的线性关系式

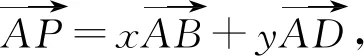
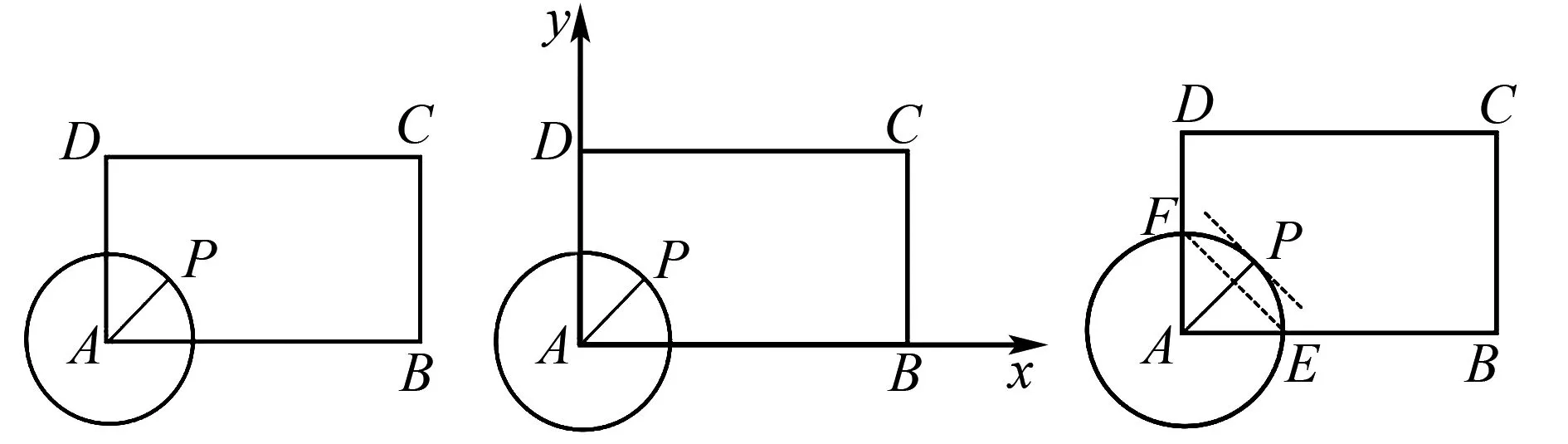
图6 图7 图8

=9x2+4y2

=(3x+2y)2-12xy

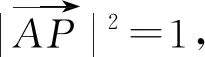
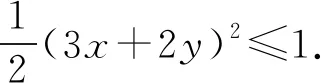
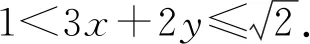
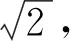
根据等和线定理，得

当点P位于等和线EF上时,(3x+2y)min=1；

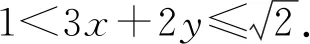
观察三个例题的解法，常规解法是通过相关知识构建出二元二次方程，此时较难求出系数之和，这为解题增添了难度.而采用等和线法则是巧妙地将复杂的求值、最值等一系列代数问题转化为几何问题，将具体的代数式运算转化为距离的比值问题，用统一的数学模型解决向量双变量问题，完美地呈现了数学的数形结合之美，也充分体现了等和线解决双变量问题的简洁性、高效性.

向量等和线以平面向量基本定理为基础，即一个向量可以用一组不共线的向量表示出来，此时两基底的系数共同决定了第三条向量终点的位置，常用的结论是当系数之和为1时，即三条共起点的向量的终点在同一条直线上.由于高考题中很多向量题目都涉及双变量系数和的问题，在遇到这类问题时，解题大体上可分为以下三个步骤：确定等和线值为1的线(即两个基底的终点所在的直线)；平移该线，结合动点的可行域，分析何处取得最大值和最小值；从长度的比值或点的位置两个角度，计算最大值和最小值，如此便求得系数和的范围.

而对于求解两个系数的一般线性关系式问题，由于向量可以通过数乘运算将向量进行同向或者反向伸长、压缩，所以所有系数的线性关系式都可以通过改变向量的基底，将所求系数的线性关系式转换为两个新的基底的系数和问题，最后再利用等和线三步骤解决问题.