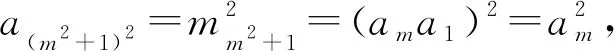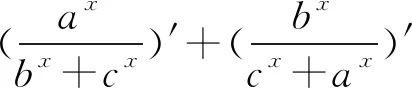2022年全国高中数学联赛(四川预赛)试题及解析

张 君

(四川省温江中学 611130)

2022年全国高中数学联赛(四川预赛)试题，全卷共11道题，其中8道填空题，3道解答题.命题组对8道填空题，只给出了答案，没有解析过程，3道解答题各提供了一种解法供阅卷参考.笔者对每道题都进行了分析和研究，逐个给出解析，解答题还给出了有别于参考答案的精彩解法，供读者参考.

该试题涉及代数运算(第1题)，平面向量(第2，9题)，数列(第3，5，10题)，平面解析几何(第4，9题)，函数与数列(第5题)，函数与方程(第7题)，函数与不等式(第11题)，解三角形(第6题)，立体几何与组合数学(第8题).

题1 已知正实数a，b满足ab=(8a)9b，则loga(4a2)的值为____.

解析由ab=(8a)9b，得b=9bloga(8a).

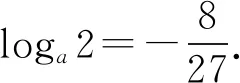
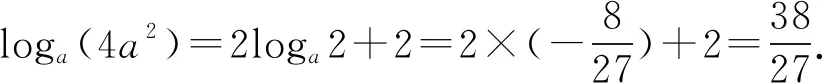
题2 已知平面向量a，b满足：|a|=1，|b|=2，a·b=1，记向量a+2b与2a-b的夹角为θ，则cosθ的值为____.

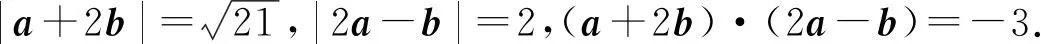
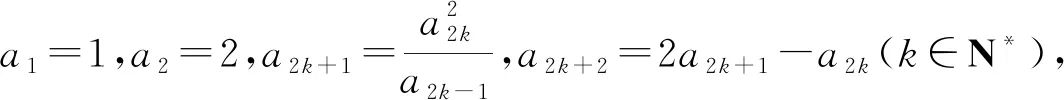
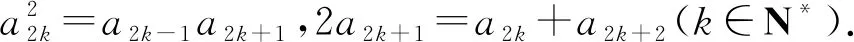
又a1=1，a2=2，所以a3=4，a4=6，a5=9，a6=12，a7=16，a8=20，…

观察归纳奇数项得a2k+1=(k+1)2.

即a2k=k(k+1).

所以a2022=1011×1012=1023132.

所以a2022的末两位数字为32.

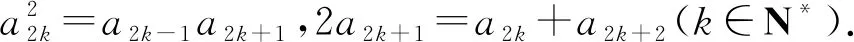
又a1=1，a2=2，所以a3=4，a4=6，a5=9，a6=12，a7=16，a8=20，…

观察归纳偶数项得a2k=k(k+1).

所以a2022=1011×1012.

所以a2022的末两位数字为32.

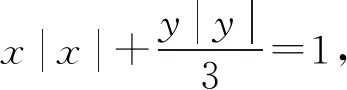
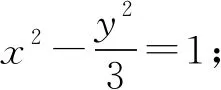
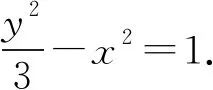
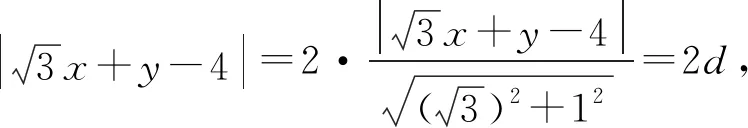
图1

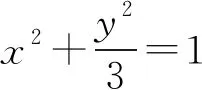
题5 已知函数f：{1,2,…,10}→{1,2,5}，且对一切k=1,2,…,9，有|f(k+1)-f(k)|≥3.则符合条件的函数个数为____.

解析由f(k)∈{1,2,…,5}且|f(k+1)-f(k)|≥3知f(k)≠3.

(问题一般化)设函数fn：{1,2,…,n}→{1,2,…,5}，且f1(1)≠3，当n≥2时，对一切k=1,2,…,n-1，有|f(k+1)-f(k)|≥3.

记函数fn的个数为an,其中满足fn(n)=1或5的个数为bn,满足fn(n)=2或4的个数为cn,则an=bn+cn.

当n≥2时，对一切k=1,2,…,n-1，若fn(k)=1,则fn(k+1)=4或5；若fn(k)=2,则fn(k+1)=5；若fn(k)=4,则fn(k+1)=1；若fn(k)=5,则fn(k+1)=1或2.

所以，当n≥3时，bn=bn-1+cn-1，cn=bn-1,则bn=an-1,cn=bn-1=an-2.

故an=an-1+an-2.

易得a1=4,a2=6,递推可得a10=288.

题6 若△ABC的三边a，b,c满足a2+b2+3c2=7，则△ABC面积的最大值为____.

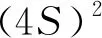
=(a+b+c)(a+b-c)(a+c-b)(b+c-a)

=[(a+b)2-c2][c2-(a-b)2]

=-(a2-b2)2+2(a2+b2)c2-c4

=-7(c2-1)2+7≤7，

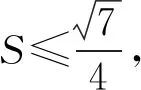
解法2 设AB边上的高为h，则

所以c2≤14-6c2-4h2.

即7c2+4h2≤14.

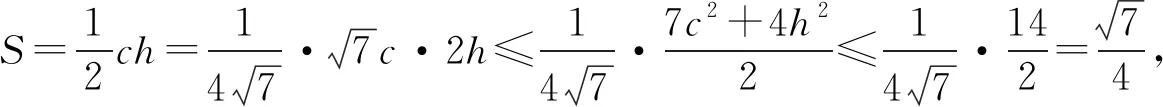
解法3 设AB边的中点为D，则

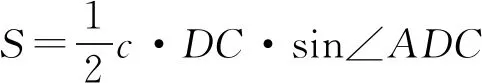
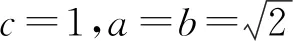
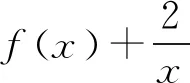
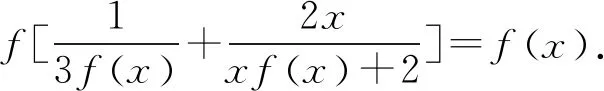
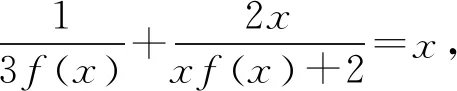
所以g(x)的最小值为3.

题8 至少通过一个正方体的3条棱中点的平面个数为____.

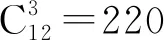
所以共有220-139=81个.

题9 如图2所示，ABCD是一个矩形,AB=8,BC=4,M,N分别是AB,CD的中点,以某动直线l为折痕将矩形在其下方的部分翻折,使每次翻折后点M都落在边CD上,记为M′.过点M′作M′P⊥CD交直线l于点P，设点P的轨迹是E.

图2

(1)建立恰当的直角坐标系，求曲线E的方程；

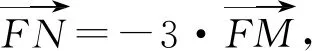
解法1(1)以MN的中点为原点O，与AB平行的直线为x轴建直角坐标系，得A(-4,-2)，B(4,-2)，M(0,-2),N(0,2)，直线CD方程为y=2，|PM′|=|PM|.

所以曲线E就是在矩形ABCD内以M为焦点、CD为准线、开口向下的一段抛物线，所以曲线E的方程是x2=-8y(-4≤x≤4).

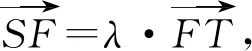
即λ=2a2.

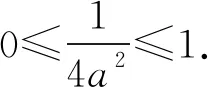
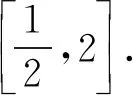
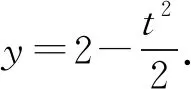
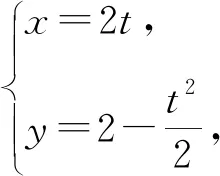
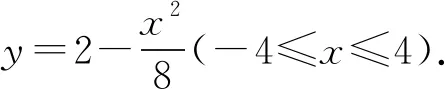
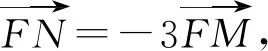
消元，得x2+8kx-8=0.

①

所以x1+x2=-8k，x1x2=-8.

②

因为方程①在[-4,4]上有两个不相等的实根,

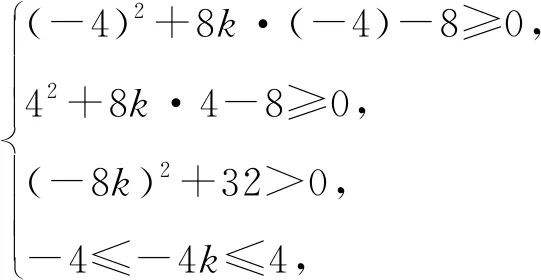
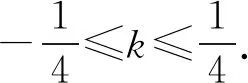
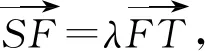
所以x1=-λx2.

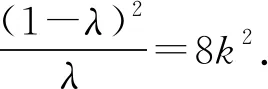
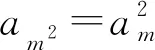
解析对任意的正整数n,都有an=1.

下面用数学归纳法证明这一结论.

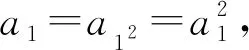
a2=a12+12=a1a1=1；

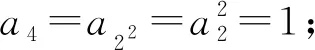
a5=a22+12=a2a1=1；

假设结论在n

(1)若k为偶数，令k=2m(m≥3)，注意到(2m)2+(m2-1)2=(m2+1)2.

一方面，a(2m)2+(m2-1)2=a2mam2-1；

从而a2m=am2-1=1，即ak=1.

(2)若k为奇数,令k=2m+1(m≥3),注意到(2m+1)2+(m-2)2=(2m-1)2+(m+2)2.

则a(2m+1)2+(m-2)2=a(2m-1)2+(m+2)2.

所以a2m+1am-2=a2m-1am+2.

因为am-2=a2m-1=am+2=1，

所以a2m+1=1，即ak=1.

由(1)(2)知，ak=1，即结论对k也成立.

由归纳原理知，对任意的正整数n，都有an=1.

所以,所求数列的通项公式为an=1.

要证原不等式，即证M-N≥0.

不妨设a≥b≥c>0，再设

A=(b+c)·ar-a·(br+cr),

A′=(b+c)·(br+cr)，

B=(c+a)·br-b·(cr+ar),

B′=(c+a)·(cr+ar)，

C=(a+b)·cr-c·(ar+br),

C′=(a+b)·(ar+br)，

所以A+B+C=(b+c-b-c)·ar+(c+a-c-a)·br+(a+b-a-b)·cr=0，

A=ab·(ar-1-br-1)+ac·(ar-1-cr-1)≥0，

C=-ac·(ar-1-cr-1)-bc·(br-1-cr-1)≤0，

A+B+C=0，A≥0，C≤0.

①

即A′=(b+c)·(br+cr)≤(a+c)·(ar+cr)=B′≤(a+b)·(ar+br)=C′.

即0

②

即M-N≥0.

经过计算可得

所以f(x)在[0,+∞)上单调递增.

因此当r>1时有f(1)≤f(r)，即原不等式成立，当且仅当a=b=c时等号成立.