基于单光子计数激光雷达的Bayesian检测研究
2022-09-22苏志刚刘卓伟
苏志刚,刘卓伟
(1.中国民航大学电子信息与自动化学院,天津 300300;2.中国民航大学中欧航空工程师学院,天津 300300)
1 引 言
单光子计数激光雷达具有高灵敏度和精准计时特性,相比普通激光雷达具有更远的探测距离和精准的测量分辨率,如今在各个领域都被广泛的使用,包括三维成像,大气探测以及地形测绘等[1]。单光子计数激光雷达通过发生激光脉冲,记录目标散射返回的光子飞行时间并重复多次将回波信号累加[2-3]。在此过程中不仅会接收到信号的回波光子,由于背景光的存在,噪声也会混杂其中,因此需要对接收数据进行检测以区分目标与背景噪声。常见的方式是设置一个阈值,当信号超过阈值则认为是目标存在,反之认为只有噪声及干扰。阈值的大小直接决定着检测效果,所以确定一个合适的阈值是检测的核心。当前单光子激光雷达的检测相关思路或多或少都借鉴了微波雷达领域的检测方法。但是微波雷达不存在累积计数过程,数据量不如单光子雷达,因而相对微波雷达,基于概率的检测方法更加适合单光子激光雷达。另外,单光子激光雷达具有相对固定的探测距离范围,目标过近时会导致严重的测距漂移,而过远会难以探测到目标,因此为确保单光子激光雷达的探测性能,在探测之前通常需要对目标距离有一个大致的预估计。检测时可依此估算出回波信号平均光子数作为先验信息,先验信息能提升检测效果,所以通常,激光雷达能得到比微波雷达更好的检测效果。预估计值越准确,则先验信息的一致性越好,对应的检测效果愈佳。
目前的单光子激光雷达检测大致可分两种类型:恒虚警(Constant false alarm)检测和固定阈值(fixed threshold)检测。其中,恒虚警检测法[4-6]较为常用,主要因为无需先验信息,其虚警概率可以保持恒定,但是在低信噪比情况下会造成检测概率降低。其次是固定阈值检测,其中有半阈值法检测[7]、似然比检测法[8]等,都是一些具有代表性的方法,它计算比较简单但是对先验信息的一致性要求较高且阈值无法根据噪声变化调整,只适合于少次累积情况而在实际工程中难以直接使用。
针对以上问题,本文提出了一种基于Bayesian准则的检测方法,该方法降低了对先验信息的一致性要求,并更加能适用于低信噪比情况。传统获取先验信息的方法都需要较精确估计距离,本文方法仅需要预估计目标的距离范围,进而将估算的信号回波平均光子数限定于某一数值区间,降低了操作难度。通过仿真与实验进行对比验证,此方法能应对各种不同累积次数情况以及各种强度的噪声变化。在低信噪比情况下的检测性能也高于其它方法。
2 单光子激光雷达概率模型
单光子雷达有多种工作模式,本文仅讨论短死时间模式。另外由于暗计数情况很小,将其忽略。假设发射器出射脉冲为调Q型高斯脉冲,假设信号发射信号功率为Pe,有表达式:
Pe(t)=βexp{-[(t-t0)/2σ]2}
(1)
其中,β表示信号的峰值功率;σ相当于方差,决定着脉冲的宽度。令激光器与目标之间的距离为R,单光子激光雷达的回波平均光子数会受到R的影响,与R2成反比[9],此外还受到雷达硬件系统、大气因素以及目标反射特性的影响。将这些综合影响用一个参数G表示,脉冲飞行时间为td,可以用激光雷达方程描述对回波光子数的变化[10]。即:
(2)
式中,R=ctd/2,c为光速。G参数一般情况下已知,只要能预知R的大概范围,通过式(2)可以确定回波平均光子数范围。
单光子雷达的发射脉冲后,系统将启动探测器进行信号接收,同时内部时钟进行计时,在历经时间长度Tg后截止,令计时器精度为τbin。在信号接收前,信号在时间t上连续。而雷达回波接收后经信号处理后将其变为离散型的时区,每个时区长度为τbin,数量达Tg/τbin个,从0开始对时区按顺序编号,用整数z表示。假设背景噪声在Tg内稳定无随机涨落且服从均匀分布。将第Z区间上噪声平均电子数表示为λn(z),信号平均光子数为λs(z)。由光电探测半经典理论可知,单光子条件下,回波信号光子统计规律可用泊松分布表示,在时区z上发生k次光电子事件的概率为:
Pk(z)=λ(z)ke-λ(z)/k!
(3)
式中,λ(z)=λn(z)+λs(z),单光子激光雷达依靠雪崩光电二极管(avalanche photon diode,APD)进行光子)测,而它既无法识别光子来源,也无法识别光子数量[11],只能识别光子的“有(一个或多于一个光子)”和“无(零个光子)”,根据(3),理想情况下时区z上此两种情况的概率分别为:
(4)
但是雪崩光电二极管具有死时间效应[12]。将死时间时长记作d,若要在Tg内的第z区间“有”光电子事件,必须保证在(z-1-d/τbin~z-1)区间内“无”光电子产生,则时区z上对应的概率Pλ(z)为:
(5)
Pλ(z)的意义是在Tg之内,时区z上平均光子数为λ时发生光电子事件的概率[13]。式(5)若λ(z)分别取值λs(z)和λn(z),则对应结果记为Ps(z)和Pn(z),表示信号与噪声的PDF,此两变量下文也将用到。单光子雷达的计数操作实际上是重复脉冲的过程,因而概率模型也是基于单次探测概率的重复模型,自然的可使用二项分布。记累积次数为M,将时区z上的光子累积数记为y,概率记作Pz(y),将式(5)代入二项分布可得[14]:
(6)
通过二项分布,单光子触发的概率转化成了多累积下光电子事件的次数的概率[15-16]。
3 Bayesian检测
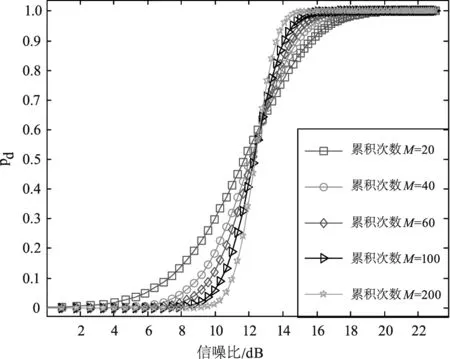
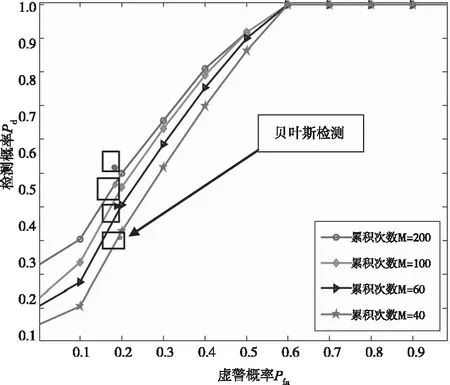
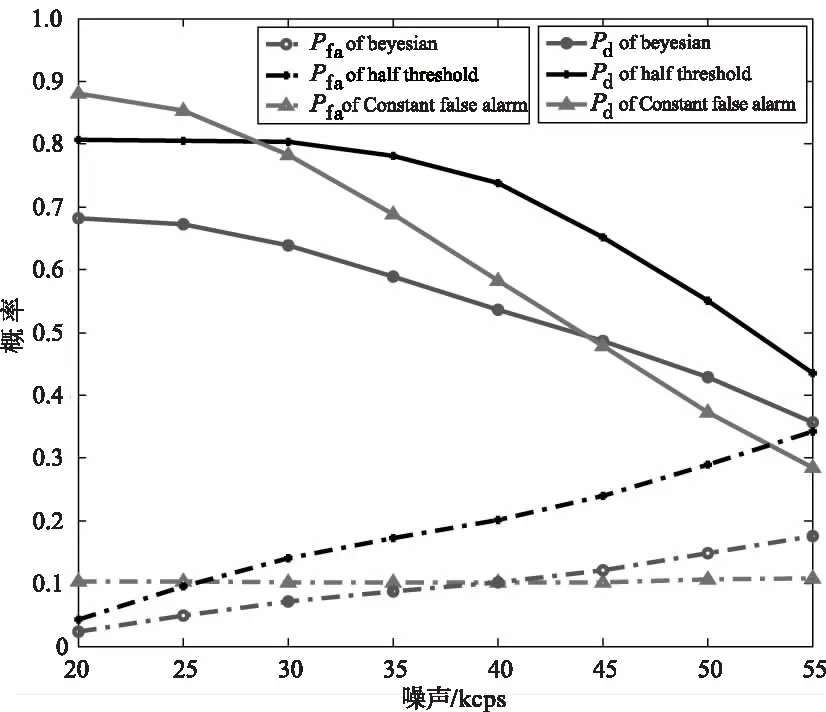
令L=Tg/τbin,则经过M次累积之后的信号具有L个时区,每个时区对应一个光子累积数y,将每个时区的光子事件发生次数记作变量yi(0≤i y≡[y0,y1,y2…yL-1] 单光子激光雷达的目标检测对应判断回波信号的峰值是否为目标。在检测接收信号在第z时区上是否存在目标时,存在两种情况:测量值不含回波目标,对应PDF标记为p(y|H0),或者测量值为干扰和回波目标之和,对应PDF标记为p(y|H1)。已知每个时区满足独立同分布条件,结合式(5),则可以得到p(y|H1),p(y|H0)分别为: (7) 将式(7)代入Bayesian准则[17]: (8) 式中,α是与代价函数相关的未知数,显然当α=1时为最小平均错误概率检验。式(8)中右边的先验概率p(H0)与p(H1)分别取Ps(z)和Pn(z)。本文所提到的“信噪比”定义皆为“信号与噪声的平均光子数的比值”,由式(8)可计算得: (9) (10) (11) (12) (13) 注意到,式(13)只能计算整数的虚警概率,而求出的阈值T常常是非整数,为了得到连续的虚警值,将T写为整数+分数的形式: T=[T]min+q=[T]max-Q (14) 则存在未知数δ(δ>0)使得: (15) 令Q+q=1,则有: (16) 由此得到连续变化的虚警概率,这种计算方式有助于绘出平滑的性能检测曲线图进而判断其检测效果。 为了比较分析检测性能,首先建立以下仿真环境,令发射端参数的发射激光束的发散角θ=3°,发射光学的系统透过率θT=90%,接收光学系统透过率ηR=80%,对于大气干扰情况,激光脉冲在大气中的透射率θa=65 %,假设发射系统光轴与目标法线方向的夹角θ=77 %,探测器死时间长度d=50,令单目标的距离R=5000 m,总时区间数量为L=3000,计时精度为0.5 ns。仿真通过观察不同信噪比情况,计算了不同累计次数下Bayesian阈值与半阈值法的检测概率Pd、虚警概率Pfa的变化。为对比检测性能,半阈值法检测为固定阈值的经典方法之一,仿真从信噪比和累计次数两方面来分析对比了Bayesian检测、半阈值法检测(half threshold)以及“恒虚警检测”的检测性能。 首先比较Bayesian检测法和半阈值法,此两者都需要先验信息,令R1R1分别为4700和5300,对应Δ=78%,为了展示不同累积次数下两种检测方法的效果。将信噪比变化范围设置在1 dB到23 dB之间,绘出了目标检测概率pd以及虚警概率pfa随信噪比变化的曲线如图1所示,其中(a)(b)分别为半(阈值法的检)概率、虚警概率的性能曲线,其中(c)(d)分别为Bayesian检测的检测概率、虚警概率的性能曲线,通过观察可以看到,半阈值法作为一种固定阈值。在信噪比降低会产生较大的虚警,而Bayesian检测表现相对稳定。 (a)半阈值法的检测概率性能曲线 显然,半阈值法仅仅适用于低累次数下适用(M<40),半阈值法对于较多累计次数下显得阈值过高,检测效果反而变差。Bayesian概率检测在累积次数少时,检测虚警略高于半阈值法,而随着累积次数增多,检测概率远远大于半阈值法,且在低信噪比情况具有更好的检测概率更高。 恒虚警检测不涉及先验信息,为了展现与Bayesian检测的效果的差异,通过蒙特卡洛实验统计10000次的不同累积次数下仿真数据,比较两者的检测概率pd变化,示意图如图2所示。 图2中空心点曲线为恒虚警检测性能曲线,实心点为对应累积次数下Bayesian检测点,可见单光子雷达的累积过程具有提高信噪比的作用。显然,由于恒虚警未知先验信息,在低信噪比下的检测概率也会很低,而Bayesian检测的阈值是同时均衡了虚警概率和检测概率的结果,能够更好地适合低信噪比的情况。 图2 Bayesian与恒虚警检测性能对比 为了进一步验证其检测效果,本文选取了搭配了64×64的APD面阵探测实验装置,该装置采用固体激光器,使用被动调Q技术产生重复频率20 kHz高斯激光脉冲,脉冲宽度约为20 ns,使用高精度时钟装置来测量脉冲飞行时间。计时单位精度是2 ns,计数次数可达20000,累积时间为1 s。实验采用了单束激光的泛光照方式,在正上方对约450 m远的目标直接凝视成像。泛光照效果类似手电,在光束中心位置光强较强,边缘光强较弱。如图3所示,其中(a)和(b)为被探(物)的(实)片与该系统的成像效果比较。 实验通过控制接收镜头的衰减镜片,在不同的参数下得到了两组数据,分别记A组与B组,其中A组的平均噪声约为20 kcps,射脉冲能量为50 μJ,B组的平均噪声约为8 kcps,射脉冲能量为300 μJ,A组的信噪比与B小越15倍,其Δ分别等于 70 %,80 %,对于本实验系统来说,在面阵上的误差点低于150个像素点可认为成像效果优良,则设置“恒虚警”的虚警概率为0.04。图(c)~(e)和(f)~(h)分别为A组和B组数的Bayesian检测、半阈值法检测和“恒虚警”检测的结果,通过对比(c)~(e)可以看Bayesian检测方法可以较为完好的检测到目标,而半阈值法导致较高的虚警使检测效果变差,恒虚警检测的虚警概率较高。综合来说Bayesian检测表现最好。 图3中(f)~(h)为信噪比较高时的结果,信噪比升高时三种检测方法皆有提升,三者中Bayesian检测依然保持较好的检测性能。综合来说,三者之中,Bayesian检测具有更好的抗噪性能。为了进一步测试三种检测方法在噪声变化时的性能,实验保持发射脉冲能量50 μJ不变,逐渐增加噪声水平,使用蒙特卡洛实验,重复次数为40960次,得到如图4所示统计结果。 (a)雷达目标照片 (b)雷达成像效果 可见随着噪声强度增加,三者的检测概率逐渐降低,虚警概率不断增加,其中,恒虚警的检测概率下降速率最快,虚警概率变化稳定,半阈值法下降缓慢,但是虚警概率急速上升,显然,Bayesian检测概率曲线大致为前两者的平均,因此,Bayesian检测法更能适应噪声变化。 图4 蒙特卡洛统计结果 本文针对单光子激光雷达目标的检测问题,构建了使用先验信息的概率模型,提出基于Bayesian检测方法,能在较小的计算量情况下,拥有良好的检测效果。该检测方案考虑了雷达累积次数,能够适应较低的信噪比情况,并且拥有较为均衡的检测效果。通过仿真以及实验对Bayesian检测、半阈值法检测和恒虚警检测方法进行了对比,低信噪比下Bayesian检测结果远远优于半阈值法和“恒虚警”检测结果。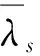
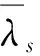
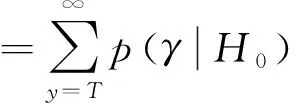
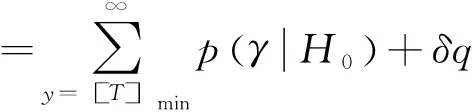
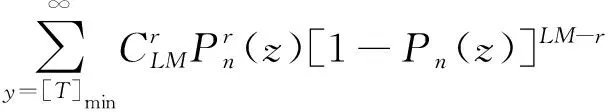
4 结果及分析
4.1 仿真及分析
4.2 实验分析

5 结 论
