低附着路面下四轮独立驱动电动汽车稳定性控制

严运兵，易振宇，杨 勇

（武汉科技大学汽车与交通工程学院，湖北 武汉 430065）

1 引言

四轮独立驱动电动汽车是当前国内外纯电动车研究领域热点之一，该结构车辆将驱动电机直接安装在驱动轮内或驱动轮附近，四轮驱动力矩独立控制，独立调整[1]。相比于传统车辆，四轮独立驱动电动汽车取消了冗长的传动链，直接将控制施加在各车轮处，为动力学控制带来了新的实现方式[2]，可以更好的提高车辆的稳定性控制和安全性。

目前，稳定性控制研究主要集中在控制算法设计和力矩分配两方面[3]，并采用分层结构。文献[4]中用PI控制得出直接横摆力矩，差结合动驱/制动转矩协调控制策略分配四轮转矩，但控制策略仅适用于低速质心侧偏角较小的工况，高速时质心侧偏角增大。文献[5]中研究车辆在紧急避障工况中的车辆稳定性问题，采用线性二次型控制算法，对纵向力进行转矩优化分配，实验验证中仅考虑低速低附着路面情况下的仿真验证。文献[6]中根据模糊规则决策出车辆稳定所需要的附加横摆力矩，充分考虑电机和路面附着系数的约束进行横摆力矩分配，但仅只在高速高附着路面验证了策略的有效性。

主要研究四轮独立驱动电动汽车在低附着路面上的操纵稳定性问题，基于分层控制思想，上层通过对车辆运行状态观测，通过粒子群PID算法优化决策出主动横摆力矩；下层以车辆前后轴动态载荷估计的比例计算出期望的四轮转矩，结合四轮转速和约束条件，通过电机模型输出目标四轮转矩，在低附着路面下进行试验验证，验证了粒子群PID算法优化后车辆具有较好的稳定性控制效果。

2 车辆模型建立

2.1 线性二自由度模型

线性二自由度车辆动力学模型表达式简单，包含了车身质量、前后轴侧偏刚度和轴距等反映汽车侧向运动的主要变量，因此广泛被用于计算整车稳定性控制器的期望值理想模型[7-8]。动力学方程如下：

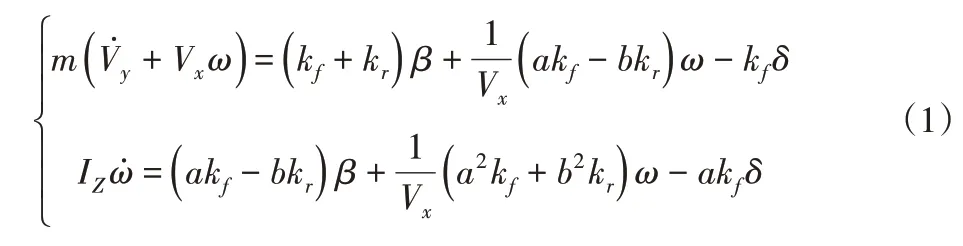
式中：m—整车质量；a、b—质心到前后轴的距离；kf、kr—前后轴侧偏刚度；d—前轮转角；Vx—纵向速度；Vy—侧向速度；Iz—转动惯量；ω—横摆角速度；β—质心侧偏角。二自由度理想模型图，如图1所示。

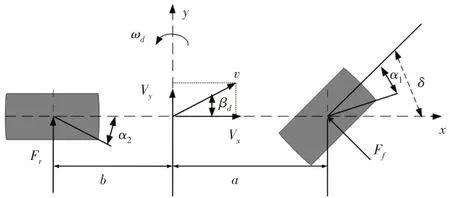
图1 二自由度车辆模型Fig.1 Two Degree of Freedom Vehicle Model

稳态时，车辆保持稳定转向，由式（1）可知，线性二自由度理想模型的期望横摆角速度和质心侧偏角为：

式中：L—轴距；ωd—理想横摆角速度；βd—理想质心侧偏角；K=—稳定性因素。

此外，质心侧偏角和横摆角速度还需考虑侧向加速度受到路面附着系数的限制[9]，因此二者极限值为：

稳态下模型参考值为：

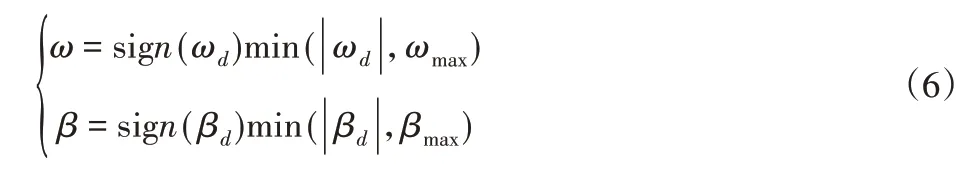
2.2 电机模型建立

本研究利用Carsim/Simulink 联合仿真模型，在Carsim 传统车辆模型中将驱动模式设置为四轮外部输入，并在Simulink中基于实物轮毂电机参数建立车辆驱动部分模型。

模型中，设定轮毂电机峰值转矩为250N·m，额定转矩为100N·m，峰值转速设定为1200r/min，电机外特性曲线，如图2所示。试验时，由上层状态观测层得到四轮转速，下层通过载荷估计转矩分配计算得到四轮理论需求转矩，通过建立的单电机查表模型，如图3所示。结合电机外特性曲线和电机力矩约束输出最终的四轮转矩。

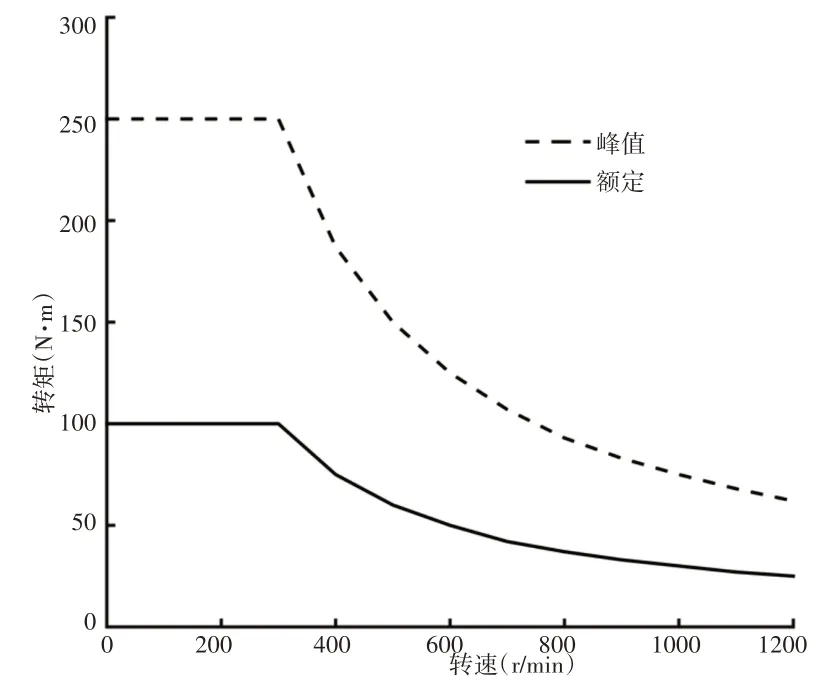
图2 电机外特性曲线Fig.2 External Characteristic Curve of Motor

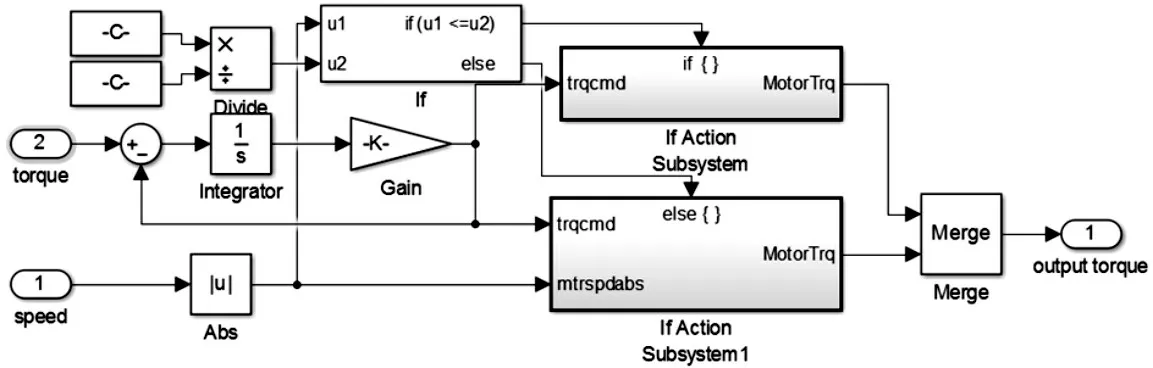
图3 单电机模型Fig.3 Single Motor Model

3 控制系统设计

3.1 稳定性控系统结构

直接横摆力矩控制（DYC）是目前汽车电子稳定性控制系统（ESC）的重要组成部分[10]。现有直接横摆力矩控制策略结构一般采用分层控制。上层为广义力决策层，根据驾驶员输入、车辆当前实际反馈信息计算所需要的直接横摆力矩和需求力矩；下层为转矩分配层，将得到的总力矩分配到四个车轮上，来改变车辆的运动状态。

控制系统的整体控制策略框图，如图4所示。设计的控制系统包括上层控制器和下层控制，上层控制器中设置汽车状态观测层获取四轮转速，通过实际车速与目标车速的差值，采用简单PID控制器获得总的需求力矩Td，除此之外，计算实际/理想质心侧偏角β和横摆角速度ω的偏差，采用粒子群PID控制器来求取直接横摆力矩Mz。

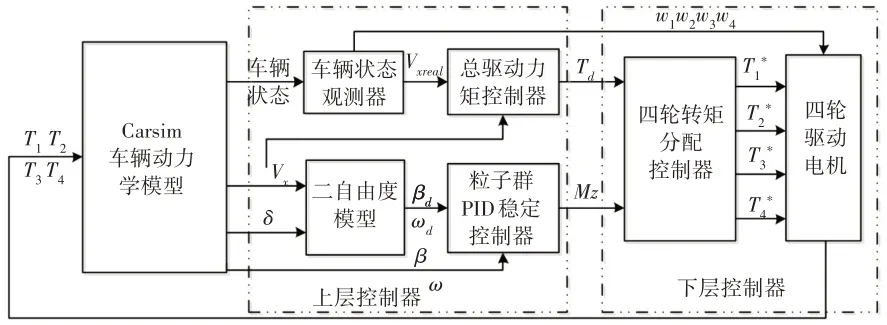
图4 整车控制策略系统框架图Fig.4 Framework of Vehicle Control Strategy System

下层控制器根据上层获得的总驱动力矩Td和直接横摆力矩Mz，在满足路面条件约束和整车动力性要求前提下，选用车辆前后轴动态载荷估计比例进行车轮转矩分配的方法，获得四轮轮毂电机需求扭矩，通过建立的电机实际查表模型在实际四轮转速下通过电机模型求解最优四轮输出转矩为T1、T2、T3、T4，分别对应左前轮、右前轮、左后轮、右后轮。

3.2 上层控制器设计

上层控制器设计基于粒子群算法优化PID参数，进行车辆稳定控制。在传统PID控制的基础上引入粒子群算法，根据输入量的偏差来在线更新系统PID的三个参数值，来获取保持车辆稳定的直接横摆力矩，达到车辆稳定性控制的效果。

直接横摆力矩获取的控制系统PID控制形式为：

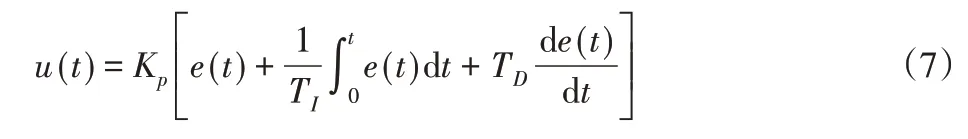
式中：u（t）—直接横摆力矩的控制系统的输出；e（t）—理想质心侧偏角和横摆角速度与实际质心侧偏角和横摆角速度的输出偏差，将理想值与实际值做差得到两者偏差，权值取0.5；Kp、T I、TD—PID控制器参数[11]。

整车稳定控制器的传递函数为：

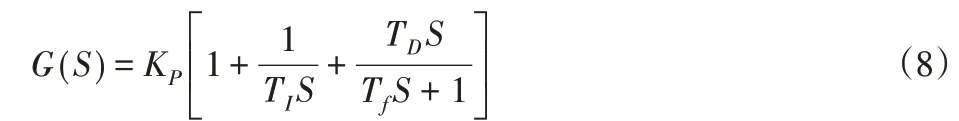
式中：Tf—滤波时间常数，根据车辆稳定性控制系统的输入量，PID控制器设置参数Kp、TI、TD的值，使输出的直接横摆力矩能够维持车辆稳定。但是当车辆工作状态发生变化，例如转向时，参数Kp、TI、TD的值若固定不变，无法适应车辆的动态系统。

为克服单一PID控制方法无法满足车辆动态系统的稳定性优化，本文引入粒子群算法对PID参数进行在线优化。PSO算法在每一次迭代过程中，粒子通过个体极值和全局极值更新自身速度和位置，更新公式如下[12]：

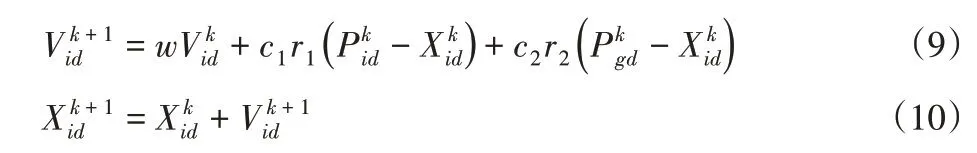
式中：d=1，2，3…，D，i=1，2，…，n；k—迭代次数；Vid—粒子速度；c1、c2—加速因子，代表粒子飞向个体最优和群体最优的加速权值；r1、r2—随机系数，范围为[0，1]；w—惯性权重。为了能均衡算法的全局搜索和局部搜索能力，加快粒子群优化算法对问题的求解速度，加入惯性权值后变化如下[13]：

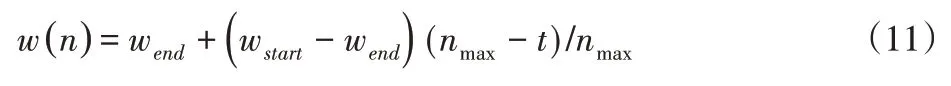
式中：wstart—初始惯性权重；wend—最大迭代次数时惯性权重；t—当下迭代数；nmax—迭代次数最大值。计算过程中，惯性权重取值w=2，加速因子c1=1.49618、c2=1.49618。粒子群优化PID的横摆力矩控制原理，如图5所示。

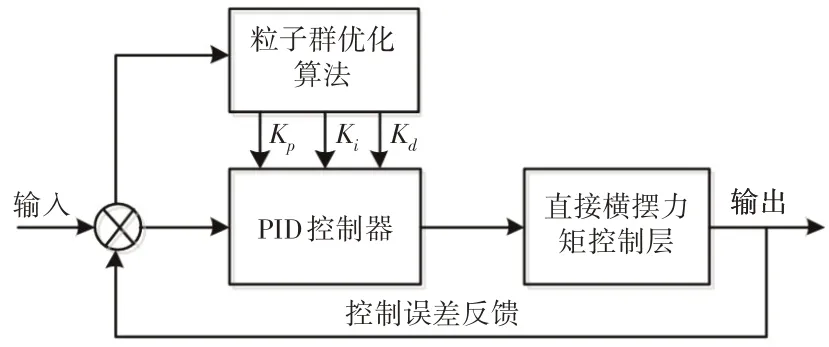
图5 粒子群优化PID的横摆力矩控制原理Fig.5 Yaw Moment Control Principle of PSO PID

先利用PID控制对建立的二自由度模型和实际车辆动力学模型反馈的质心侧偏角和横摆角速度偏差进行直接横摆力矩控制，计算控制误差，然后根据控制误差采用粒子群优化算法对目标函数中的Kp、TI、TD参数取值范围进行初始粒子化，通过粒子群最优位置对PID控制器中三个参数进行整定，以降低直接横摆力矩控制误差。

3.3 下层控制器设计

转矩分配采用前后轴的载荷估计进行的转矩分配策略[14]，假设四轮轮毂电机分配后转矩为T1、T2、T3、T4，各轮转矩需满足以下要求。首先必须能够保证车辆的正常行驶，满足纵向力分配要求：

式中：Ttol—整车纵向驱动总力矩，各轮转矩产生的整车直接横摆力矩应满足式（13）的控制需求：

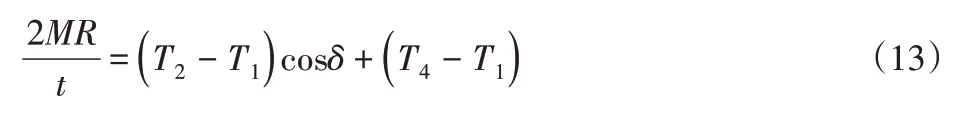
考虑到加减速的情况，汽车前后轴载荷为Fzf、Fzr，如式（14）所示：

按照前后轴载荷进行分配得到：

联立以上各式，在前轮小转角的情况下，求解方程组可得：

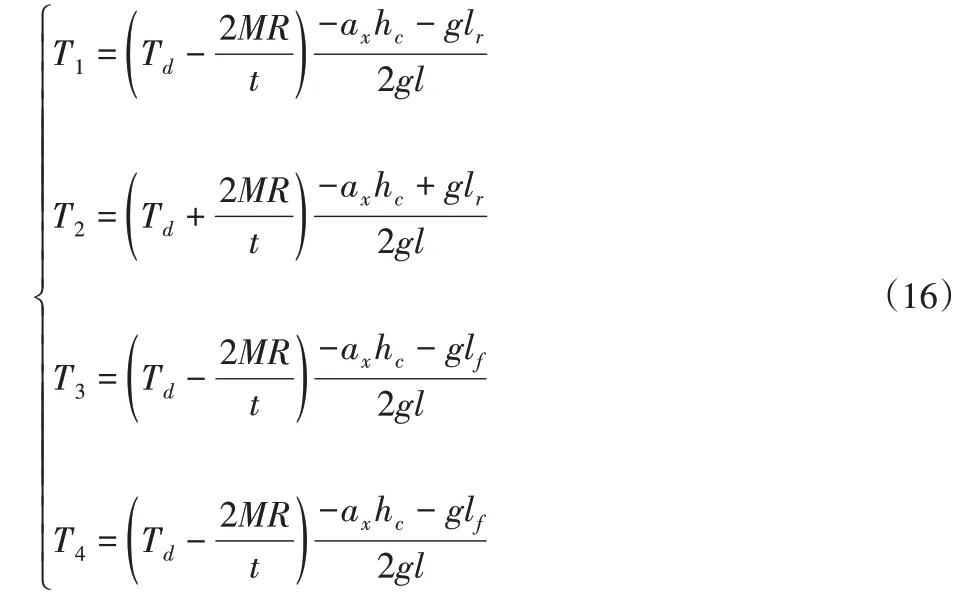
式中：T1，T2，T3，T4—轮转矩；M—整车质量；t—轮距；lf、lr—前后轴到质心的距离；l—轴距；R—车轮半径；ax—纵向加速度；hc—质心高度；cosδ近似为1；g—重力加速度。

3.4 优化问题约束条件

求得各轮的理论转矩后，需考虑路面条件约束，故建立以四轮轮胎纵向利用率平方和最小的优化目标函数，考虑路面附着极限，目标函数，如式（17）、式（18）所示：

式中：i=1，2，3，4—左前轮、右前轮、左后轮、右后轮；μi—路面附着系数；Fxi—车轮i的纵向力；Fzi—车轮i的垂向力。

同时，将轮毂电机作为理想的执行器时，考虑轮毂电机的执行能力约束条件：

式中：Tmin、Tmax—四轮驱动电机输出限值。

将以上目标函数作为转矩分配层的优化目标，利用约束条件对最终输出的驱动转矩进行限制，得到传递给电机控制器的输出驱动转矩指令。

4 仿真试验和结果分析

为验证提出的粒子群优化PID算法在低附着路面上对车辆稳定控制的有效性，利用Carsim车辆动力学软件和Matlab/Simulink仿真软件，搭建完整的四轮独立驱动电动汽车模型，选择低附着阶跃和单移线工况进行试验验证。车辆部分参数，如表1所示。

表1 车辆部分参数Tab.1 Some Parameters of Vehicle

4.1 高速阶跃转向工况试验仿真

在Carsim 中建立行驶工况，设路面附着系数为0.3，车辆以90km/h行驶4s后进入阶跃转向工况，阶跃转向角为60°，整个工况运行15s左右，如图6（a）所示。仿真结果，如图6所示。

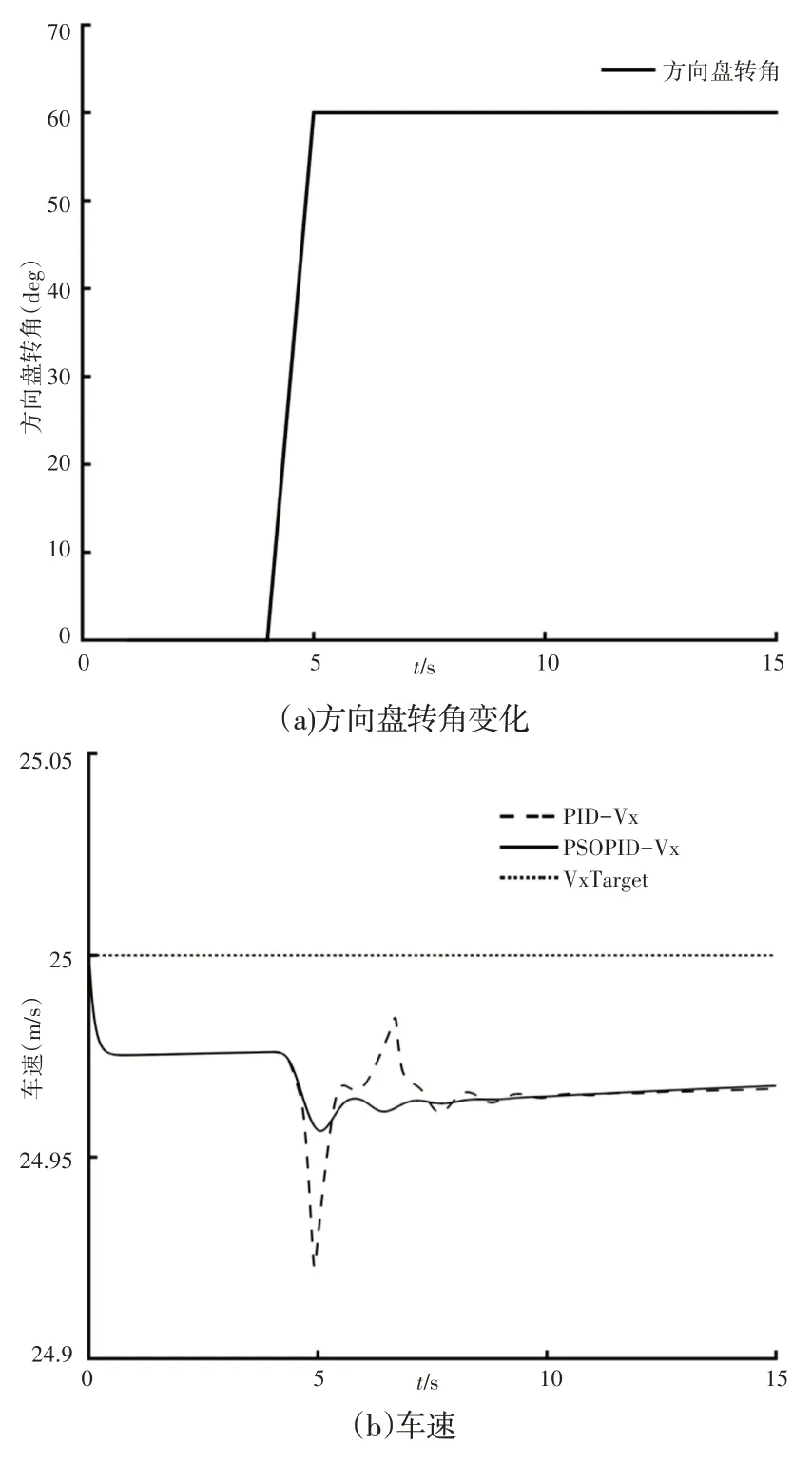
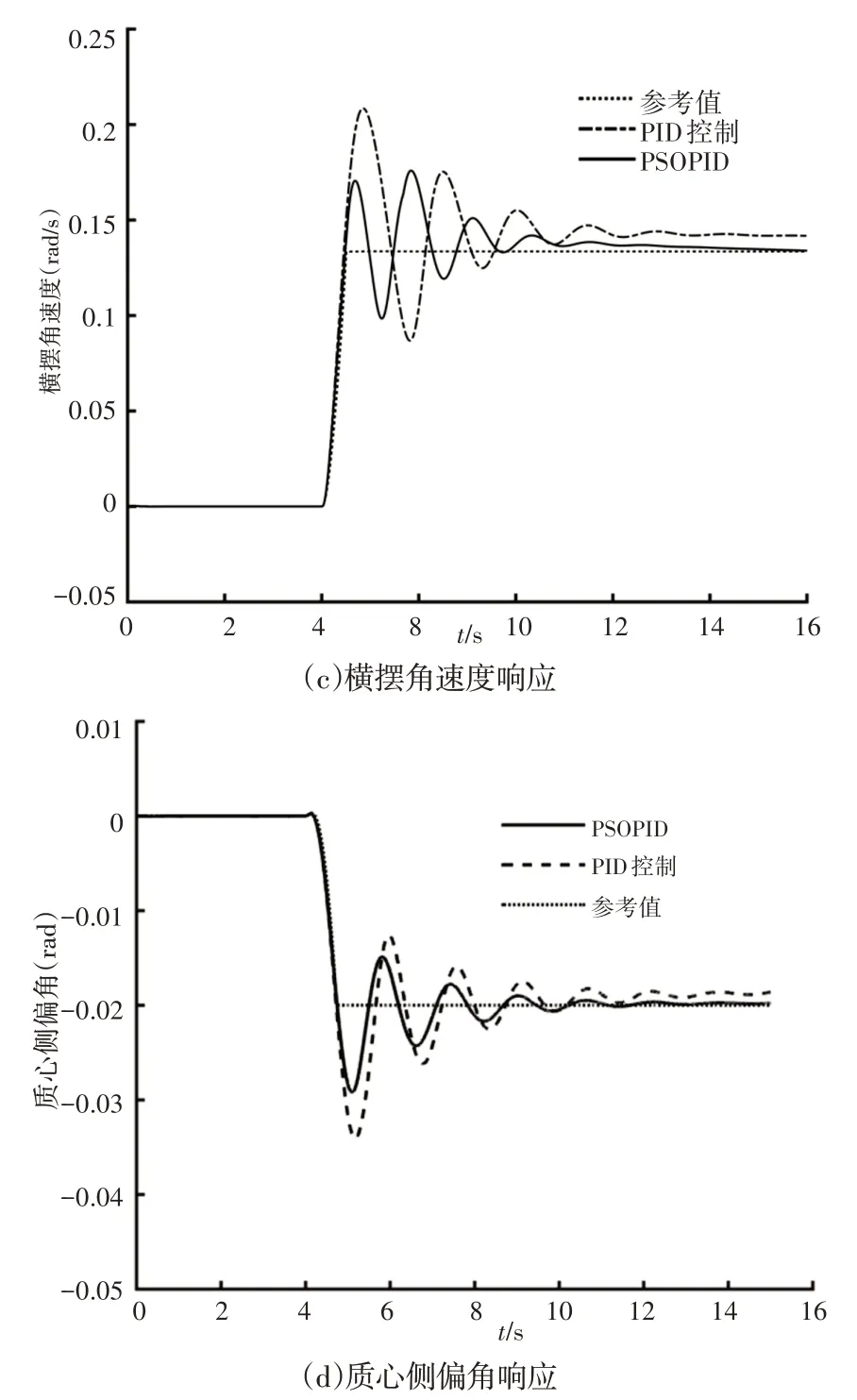
图6 低附着高速阶跃工况仿真结果Fig.6 Simulation Results of Low Adhesion and High Speed Step Condition

由图6（b）～图6（d）得出，引入粒子群算法对PID参数进行优化后，在低附着路面阶跃转向时，与普通PID控制相比，车辆车速变化相对较小，车辆质心侧偏角和横摆角速度的响应收敛速度均有所提高，由于是采用的高速低附着路面环境工况，其横摆角速度的在粒子群PID优化下超调量低于25%，因此证明车辆在粒子群PID控制情况下能够更快的恢复车辆稳定。

4.2 低速单移线工况试验仿真

单移线工况是一种方向盘以正弦角度输入的工况，设定车辆速度为50km/h，路面附着系数为0.25，在第3s时方向盘输入幅值为61.5°的正弦角度，如图7（a）所示。整个工况运行15s左右，结果，如图7所示。由图7（b）～图7（d）所示，在单移线工况下，相比普通PID控制的方法，在采用粒子群PID的优化算法后车辆纵向速度在转向过程中变化幅度较小，横摆角速度的震荡也相对得到了抑制，有效地减小了车辆的质心侧偏角，使车辆的操纵稳定性得到了提高。由以上的试验结果可以得出，四轮独立驱动电动汽车在低附着路面，当车速较低时，在普通PID控制下，其自身车身的失稳并不严重，因此低速情况下粒子群PID和普通PID的控制效果差距不大。但在高速情况下，可以明显看出普通PID控制情况下车辆的震荡比较严重，粒子群PID经过优化PID参数后可以降低车辆的震荡状态，使车辆尽快达到稳定，提高了车辆的操纵稳定性，保证汽车能够安全行驶。

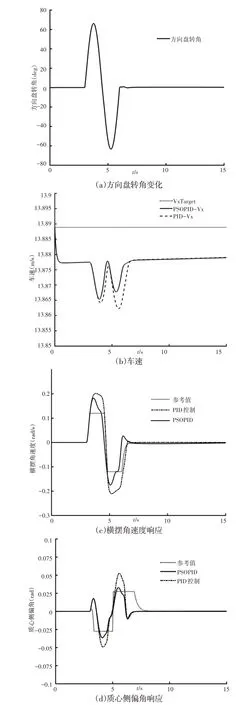
图7 低附着低速单移线工况仿真结果Fig.7 Simulation Results of Low Adhesion and Low Speed Single Shift Line

5 结论

（1）以四轮独立驱动电动汽车为研究对象，设计了分层结构的直接横摆力矩的控制策略，上层依据理想和实际的质心侧偏角和横摆角速度偏差获得总的直接横摆力矩，下层基于有约束的载荷估计进行转矩分配。

（2）为验证所提出的粒子群PID优化算法方案，通过Carsim/Simulink联合仿真，在低附着路面上选取高速阶跃和低速单移线工况进行试验。试验结果可知，相比于普通PID控制方法，在引入粒子群算法优化PID参数后的优化控制，在低附着工况下均提高了车辆质心侧偏角和横摆角速度的收敛速度，且降低了车辆的震荡状态，验证了提出的策略能够满足车辆在低附着工况下稳定行驶。

（3）提出的稳定性控制策略实现了四轮独立驱动电动汽车在低附着路面情况下的操纵稳定性控制，改善了车辆的转向特性，提高了车辆极限工况下稳定裕度。