考虑PCA-LSTM的风电机组输出功率预测研究
2022-09-22袁逸萍贾依达尔
李 明,袁逸萍,贾依达尔,赵 琴
(新疆大学机械工程学院,新疆 乌鲁木齐 830047)
1 引言
由于风力资源的波动性和间歇性特点,并网风力发电在给人类提供清洁能源的同时,也给电力系统的安全、稳定运行带来了严峻挑战[1]。精确的风电功率短期预测有助于缓解电力系统调峰、调频压力,对于风电并网具有重大意义[2-3]。同时,对于发电设备的利用率和经济调度的有效性也起着重要作用[4]。SCADA数据采集与监控系统集成在风电机组中,用于完整记录机组各个子系统和关键部件的运行状态[5]。该系统监测参数众多:既包括电机保护、偏航动作开关等离散参量,又包括温度、风速、振动、电压、电流等连续参量[6]。然而通常无法通过庞大的SCADA数据提取反应系统运行状态的特征向量,从而挖掘风电机组各运行系统之间的潜在关联性,提取特征向量精确预测风电功率是一大挑战。
国内外学者结合SCADA 数据针对风电机组相关参数的预测及故障认定做了大量研究。文献[7]分析了风电机组温度、功率等SCADA数据,震动信号的频率作为辅助因素,利用神经网络实现了风机轴承是否故障,故障等级所属,以及具体故障类型的三级故障预测;文献[7]中运用风机SCADA数据中的转速、功率为参数,建立了Boosting tree 和神经网络两种模型预测故障发生;文献[8]采用最小量化误差的神经网络,对某海上风机的故障进行了预测,效果较好;文献[9]将SCADA数据中实时功率、不可控风速、空气温度、主轴转速作为神经网络的输入,通过实际轴承温度与预测轴承温度的残差预测故障。文献[10]利用线性回归分析对齿轮箱轴承温度进行了预测;文献[12]利用SPC及SVM算法建立了轴承温度预测模型;文献[13]等利用非线性自回归神经网络对齿轮箱油温及相关变量集进行了建模采用考虑残差分布规律的SPC方法控制模型在线学习行为。
在以上预测研究基础上,选择能够充分挖掘时间维度上的信息的LSTM网络,利用PCA降维原始变量集降低冗余,最终实现风电机组短期输出功率的准确稳定预测,为缓解电力系统调峰、调频压力,发电设备的利用率和经济调度的有效性提供基础性支持。
2 建模变量定义
模型输入的数据均来自新疆地区某风场2017 年12 月的SCADA数据,模型可由式(1)进行描述。
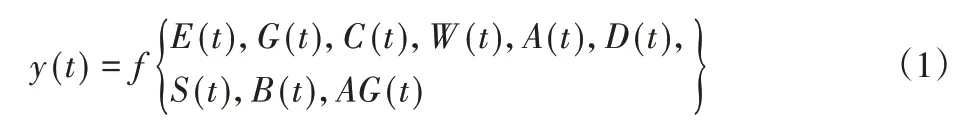
输入量包括:变流器扭矩反馈、变流器功率反馈、变流器机侧电压、风速(机械)、视在功率、发电机转速(接近开关)、gh输出变流器扭矩给定值等一些列与风电机组输出功率存在较大影响因子的相关变量。
3 模型建立
3.1 PCA数据降维
减少变量集Xt中反映同一特性的冗余变量,有益于减小模型计算量,提升精度。通过特征方程求得R矩阵的特征值λ(λ1、λ2、…、λn,λ1≥λ2≥…≥λn),再根据各个主成分累计贡献率Qs(m)选取k个主成分。数学表达式,如式(2)所示。
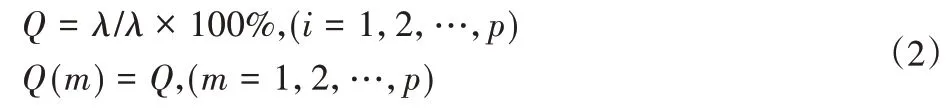
一般累计贡献率Q(m)≥85%即可包含原问题的绝大部分信息,能够较准确描述原问题的发展方向。
3.2 长短时记忆神经网络(LSTM)
由于RNN存在梯度消失的问题,所以Hochreiter和Schmid⁃huber引入记忆单元提出了LSTM,LSTM是一种时间递归型网络,主要应用于时间序列预测问题中。LSTM由输入层、隐含层和输出层组成,同时LSTM 通过输入门、遗忘门和输出门三个结构进行信息的保护和控制。在给出图1的LSTM 结构中组成输入单元,ht为状态输出单元,Ct-1,Ct表示细胞状态,it、ft、ot分别为输入、遗忘和输出门限,各单元的状态可由式(3)~式(8)表示。
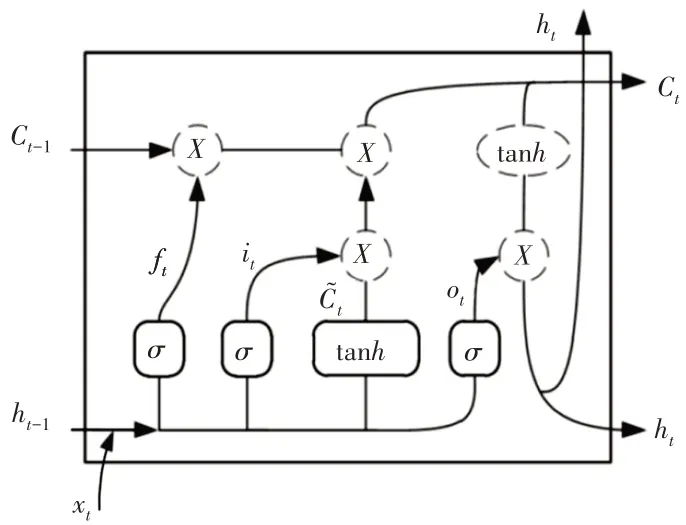
图1 LSTM结构图Fig.1 LSTM Structure Diagram
遗忘门:

输入门:

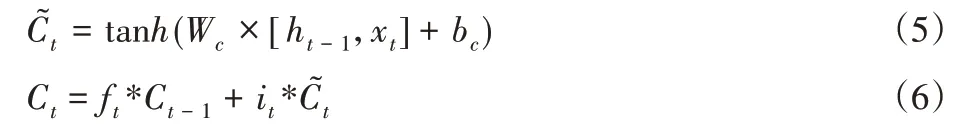
输出门:

式中:σ—sigmoid函数。
4 案例验证分析
4.1 平台与数据准备
4.1.1 平台设置
硬件平台为工作站。处理器为i5-8250U,内存为8GB,固态硬盘容量为265GB。软件框架结构为基于Anaconda深度学习工具的Tensorflow框架。
4.1.2 数据构造与评价指标说明
将2017年12月1日至12月31日期间的新疆某风场直驱永磁式2MW 机型12 号机SCADA 实际工况运维数据进行模型验证,SCADA系统每300s记录一次机组运行参数。
变量间存在强相关性是进行PCA分析的前提必备条件。变量间的相关性可由KMO(Kaisar-Meyer-Olkin)和Bartlett检验获得,检验结果,如表1所示。

表1 相关性检验表Tab.1 Correlation Checklist
KMO 检验主要是用于说明主成分提取的数据情况。根据表1,KMO 检验系数值0.857>0.8,巴特利检验系数值P=0.000<0.001,该研究数据结构良好,存在较强相关关系,具有很好的实用性,研究数据可以进行主成分分析。
对于以上数据进行数据预处理步骤如下:
(1)根据式(9)对所有数据进行归一化处理。

(2)零值及数据缺失处,直接采用将整条数据进行删除操作即可,由于总的数据量足够完成仿真,同时仅存在少量的零值及缺失,故此操作不影响总的预测效果。
(3)进行数据高斯平滑处理。
(4)据式(10)计算每个变量对于风电机组有功功率的Pear⁃son相关系数,保留系数值>0.8的变量。
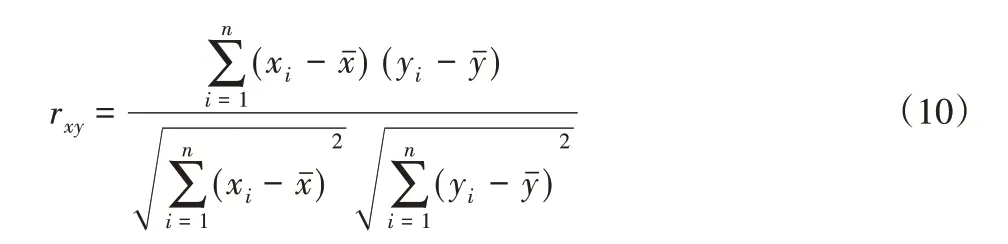
根据PCA计算原则,计算所属特征值对于输出功率提供的单个贡献了和累计贡献率,根据下表,Qj(g)≥85%的主成分包含4个,Qj(g)=89.17%,故g=4。
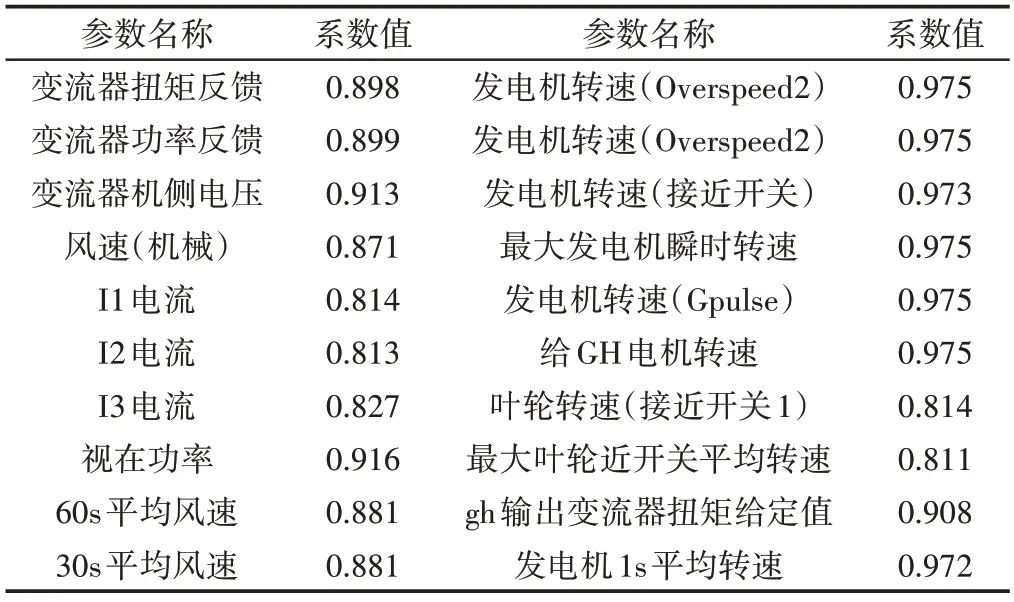
表2 相关参数表Tab.2 Related Parameter Table
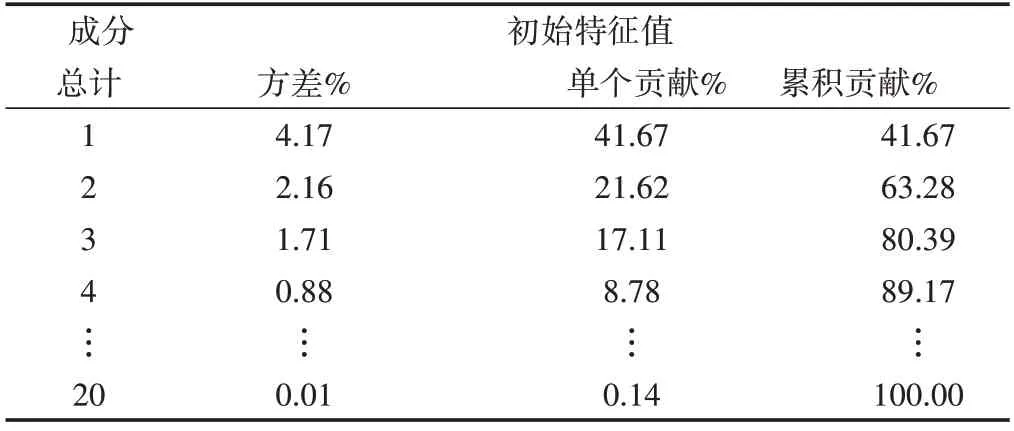
表3 总方差解释表Tab.3 Total Variance Interpretation Table
进而得到成分系数矩阵,如表4所示。

表4 成分系数表Tab.4 Composition Coefficient Table
取得以上参数样本总数为11949,将最后的500组数据作为测试集,余留数据按照4:1的比例设定训练集和验证集。选取预测步长为6步,即1h的预测间隔;与具有代表性的时间序列预测算法Arima、SVM在同一数据集对比预测效果。各模型预测性能依据以下统计误差分析参数进行衡量:
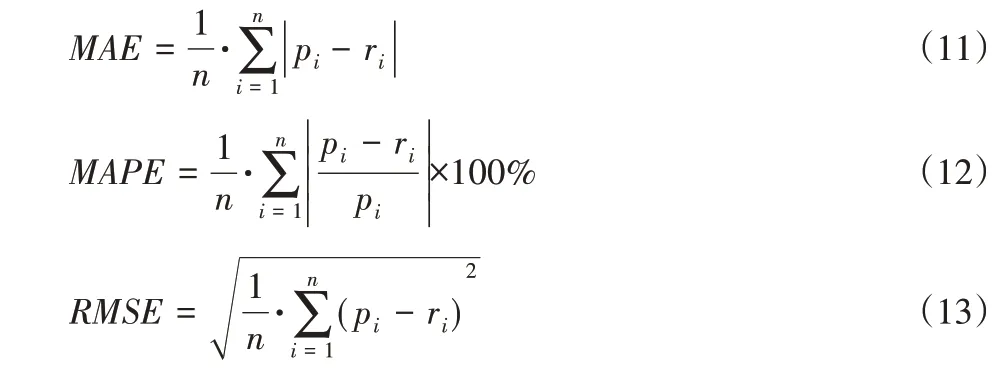
式中:pi—模型预测值;ri—功率实际值;n—样本总数;式(11)~式(13)式表征误差情况,计算结果越小表明预测值与实际值越接近,证明模型性能越好,特征表达能力越强。
4.2 预模型参数设定及案例结果分析
在LSTM算法中,将输入层设定为21,数据经过输出维度为50的LSTM单元,并取其隐含层输出形成(50×21)的数据矩阵hl。预测结果,如图2所示。
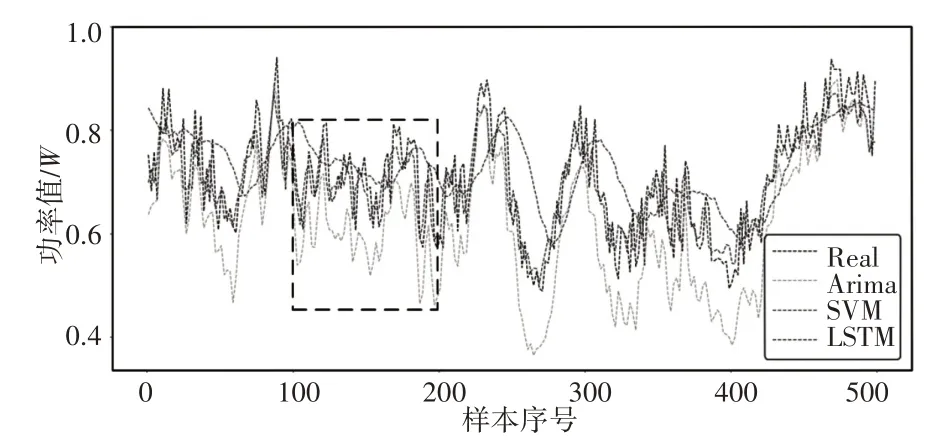
图2 预测结果图Fig.2 Forecast Result Graph
比较图2中的结果可以发现,由于步长较长,三种模型在一定程度上均偏离了原始数据集的发展方向,其中表征Arima模型预测结果的黄色线条偏离程度最大,表征SVM及LSTM预测结果的绿色及红色线条偏离程度多少并不能通过整个表现出来,如图2所示。于是将图2[100,200]区间内的点集分布进行放大形成图,如图3所示。在图3的结果中可以知道,LSTM模型预测结果始终保持与原始数据集变化趋势的紧密贴合,虽然SVM预测结果在大体上也能够跟随实际值的变化趋势,但预测图中可以发现两种现象,第一是预测结果变化的幅度总是小于原始数据集变化的幅度,呈现一种‘平稳过度’的现象;第二在图2中明显可发现,在每一段原始数据发生较大的突然下降时,表征SVM预测结果的绿色线条存在延后下降的趋势,导致严重失准。同时,表5中的误差统计结果表明,LSTM模型各项指标均优于Arima与SVM,结合各项指标,LSTM 较Arima 误差平均降低61.10%,较SVM 误差平均降低了27.85%。
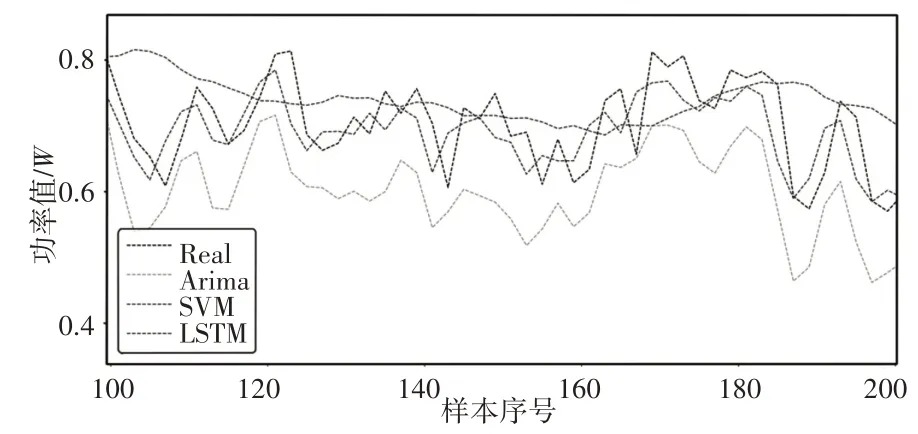
图3 预测结果图Fig.3 Forecast Result Graph
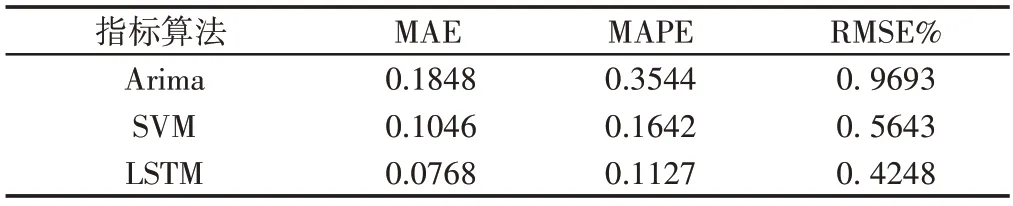
表5 误差对比结果表Tab.5 Error Comparison Result Table
4.3 结论
长短期记忆神经网络在时间序列上的预测具有优势,能够充分挖掘时间维度上的信息,从而更准确的反应短时期内的负荷变化,提升预测结果的可靠性。
然而,面对非线性数据大量长期数据预测问题时,由于记忆细胞中存储的原始记忆作用,在一定程度上中和了突变数据带来的影响,因而可能会使预测结果呈现较为平稳的变化趋势。这就在一定程度上会造成预测相应功率数值时有延迟现象,将直接导致预测精度的下降,故针对于长期非线性的数据预测应适当考虑空间信息的结合,对于高维多源异构数据空间上的特征和LSTM记忆细胞输出的时序特征向量的结合,在不同的点具有相对应的侧重点,更好的缓冲数据突变带来的数据预测不稳定性将是有待继续深入研究的一个方向。
相对于传统的预测方法提出的模型挖掘的信息更为充分,实现了数据特征的提取,预测效果也较传统预测方法有较好的精度,在预测结果上更接近实际值的非线性变化趋势,提高了短期功率预测的稳定性。
