有限元分析与支持向量机结合对2t/8.7m壁行式起重机的可靠度分析

李卫民，马继召，雷晓柱

（唐山职业技术学院机电工程系，河北 唐山 063000）

1 引言

起重机作为当前工业生产主要的物料运输机械设备，以其设计结构紧凑、传动扭矩大，在现代化生产中广为应用。在实际应用中，作业特点重复性高承载波动范围大，因此其安全可靠性至关重要[1]。长期以来起重机作业时其可靠度一直都被认定是评价其安全性的关键指标，因此针对起重机可靠度分析的研究也成为当前学术界的主要热点。

悬臂梁作为壁行式起重机中支撑系统的主要部件，承受着绝大部分外部载荷，因此针对悬臂梁的结构力学分析和可靠度分析显得尤为重要。文献[2]利用ANSYS软件构建起重机主梁模型，通过分布模拟起重载荷对主梁结构及厚度进行了优化。文献[3]应用模糊数学理论分析出运行机构隶属函数，运用函数模型预测系统的寿命。文献[4]基于断裂力学理论，建立桥式起重机主梁结构抗力和载荷时变模型，推导桥式起重机结构时变功能函数数学模型，预测起重机的寿命。文献[5]通过针对桥梁动载荷分析问题，提出了将动载系数引入到静强度分析中，有效给出了动载荷问题无法准确计算的解决方法。

该文主要针对2t/8.7m壁行式起重机可靠度展开分析，基于有限元软件ANSYS构建其有限元模型，确定边界条件，通过确定载荷在跨端、跨中两种典型工况下，确定应力分布云图。基于此结果，引入支持向量机，确定影响起重机作业时承受应力的主特征量，搭建支持向量机可靠度分析模型，通过对模型的训练和学习，有效预测起重机关键位置处的受力状况，判断其可靠度分析结果。

2 壁行式起重机有限元分析

2.1 主要性能参数

2t/8.7m 壁行式起重机起升载荷2000kg，悬臂长8.7m，起升速度5/0.8m/min，自身重量4200kg，运行速度32m/min，该设备相关详细参数，如表1所示。

表1 2t/8.7m起重机性能参数Tab.1 Performance Parameters of 2T/8.7m Wall-Crane

构建设备整体结构三维图，如图1所示。

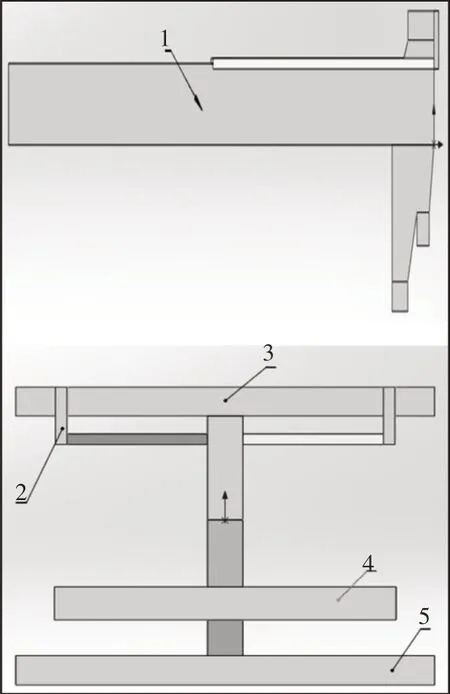
图1 设备结构三维图Fig.1 Three Dimensional Drawing of Equipment Structure

2.2 有限元模型的建立

在不影响精度的前提下，对起重机结构模型进行一定的简化。将水平支架与上翼缘板的连接处，简化为连接区域内钢板厚度的加大，结构中存在的多处螺母、垫圈等部件均可忽略。对模型中起重机与水平轨道接触处设置固定约束，利用Workbench中的Hex Dominant 对其进行六面体网格划分[6]。划分结果,如图2所示。共离散为24372个单元，78118个节点。

图2 结构三维有限元模型Fig.2 Structural Three Dimensional Finite Element Model

2.3 载荷处理和工况选择

（1）自重载荷PG及其动载效应[7]

动载效应的计算与PG有关，一般用起升冲击系数ϕ1乘以PG来考虑，其中ϕ1=1±α，0 ≤α≤0.1，本文取ϕ1=1.05。

（2）起升载荷PQ及其动载系数ϕ2[8]

ϕ2的取值，一般与起升速度、起升状态有关，ϕ2与它们之间的关系为：

式中：ϕ2min—最小值；vq—起升速度；β2—起升状态级别系数。

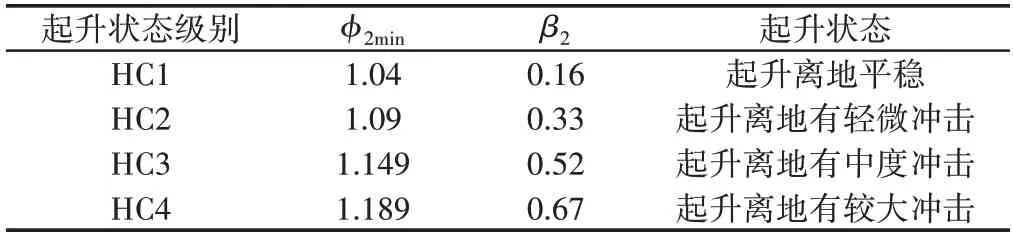
表2 ϕ2min与β2取值Tab.2 The Values of ϕ2min and β2

在此起升状态对应HC2，vq为5/0.8m/min，基于极限工况，在此取5m/min。

（3）水平惯性载荷PH及其动载系数

实际作业时产生的惯性力，记为PH。其计算公式为：

其中，ϕ5取值范围1 ≤ϕ5≤2，在此取ϕ5=1.5；m为运行部分的质量；a为起、制动的加速度，参考实际工况参数可得：

代入式（2）中，可得pH=819N

考虑到该壁行式起重机工况基本上在室内进行，可不考虑风载[9]。该壁行式设备依据载荷类别，分以下2种工况：

工况1：小车满载处于悬壁梁跨端处的位置；

工况2：小车满载处于悬壁梁跨中处的位置。

表3 两种工况下相关载荷参数Tab.3 Relevant Load Parameters

2.4 有限元计算结果分析

利用Ansys Workbench 分别对这两种工况进行加载[10-11]求解，应力分布云图，如图3、图4所示。

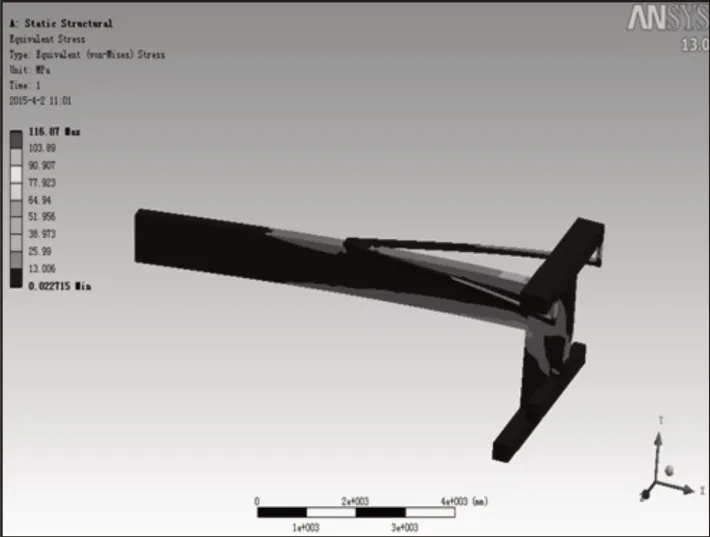
图3 工况1下应力分布云图Fig.3 Stress Distribution Nephogram of Crane Under Working Condition One

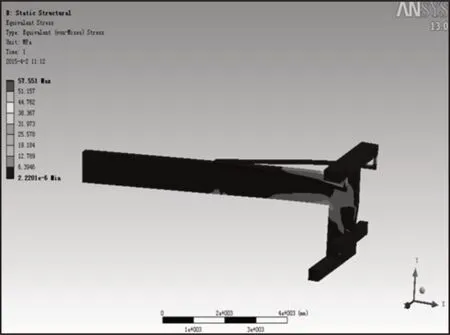
图4 工况2下应力分布云图Fig.4 Stress Distribution Nephogram of Crane Under Working Condition Two

由图3、图4可知，在悬壁梁的尾部应力波动比较集中，其中工况1 下的最大应力为116.87MPa，工况2 下的最大应力为57.551MPa，且应力现象集中出现在悬壁梁尾部的拐角处。

3 壁行式起重机受力预测方法分析

依据有限元分析结果可发现，起重机在搬运物料过程中，悬壁梁尾部拐角承受应力最为恶劣，容易发生开裂，是影响起重机可靠性的关键位置。考虑到应力波动范围不是太大，属于小样本集合，选用支持向量机对悬臂梁受力情况进行预测诊断。

3.1 构建悬臂梁受力支持向量机预测模型

起重机悬壁梁承受载荷属于线性回归问题，回归函数用式（4）线性方程来表示：

受力预测见式（5）最小值求解：

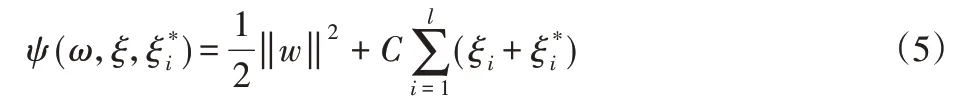
式中：c—惩罚因子；ξ，ξ∗—松弛变量的上下限。

约束条件为：

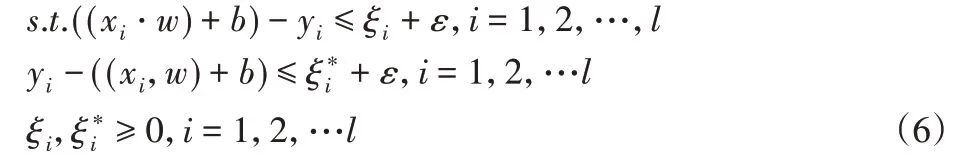
式中：ε—回归允许最大误差，引入Lagrange函数。

将式（7）代入式（4）可得：

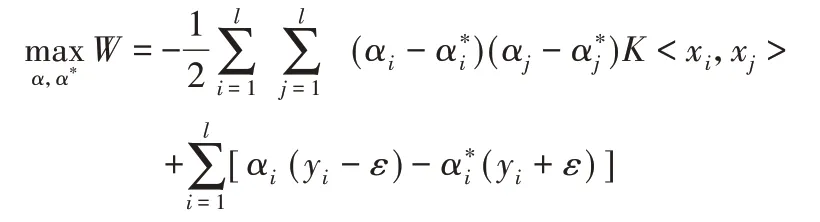
约束条件：

即支持向量机的输出为：

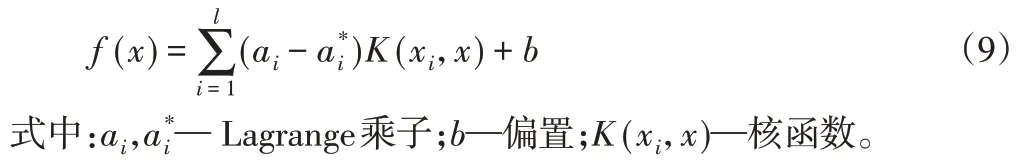
在此选用高斯径向基RBF核函数为起重机悬臂梁受力预测模型的核函数，故支持向量机的输出模型为：

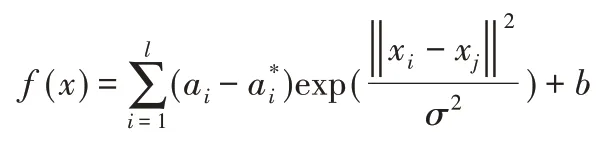
惩罚参数Ci、σi(i=1，2，…，9)还需通过构造试验，获取Ciσi(i=1，2，…，9)最优。利用支持向量机建立起重机悬臂梁受力预测模型，具体流程，如图5所示。

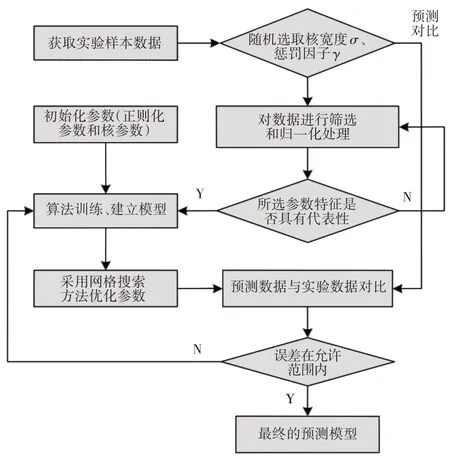
图5 SVM模型构建流程图Fig.5 Flow Chart of Support Vector Machine Model Construction

4 可靠度分析方法验证实例

利用构建好的支持向量机模型对起重机可靠度进行评估，针对受力最恶劣的部位进行应力诊断，该方法需构造实验获取特征量样本数据，对模型进行训练学习，确定模型参数最优值，最终实现预测诊断。

4.1 实验方案与训练样本的确定

起重机在工作过程中在其受力所有特征矢量中，自重载荷PG，动载系数ϕ2及加载位置W可通过查阅起重机设备参数获取。起升载荷PQ、起升速度vq及水平移动速度vH需设计试验进行样本测取。试验所需设备及测取方案如下。

4.1.1 试验设备

（1）2t/8.7m壁行式起重机；

（2）测试所需工具：接触式旋转速度传感器，称重传感器，水平位移传感器；

（3）应变片及粘贴要求：在悬臂梁拐角处粘贴电阻应变片，被贴表面保持平整、光滑，表面光洁度应达▽5左右。

4.1.2 测取方案

对起升载荷，起升速度及水平移动速三种不同特征量进行分组试验，共进行10组实验，试验中每间隔2min监测各组悬臂梁拐角处应力大小。基于测得的75组特征量样本，随机抽取55组作为训练样本，其余20组为测试样本，考虑到数量级波动较大，需进行归一化处理，部分实测数据，如表4 所示。依据样本数据，参数可设置：C=100，σ=1。通过获取的样本对SVM 模型进行训练学习，然后运用构建的支持向量机模型输入相关参数进行验证，得出悬臂梁受力预测值，将实测值与预测值进行对比，如表5所示。

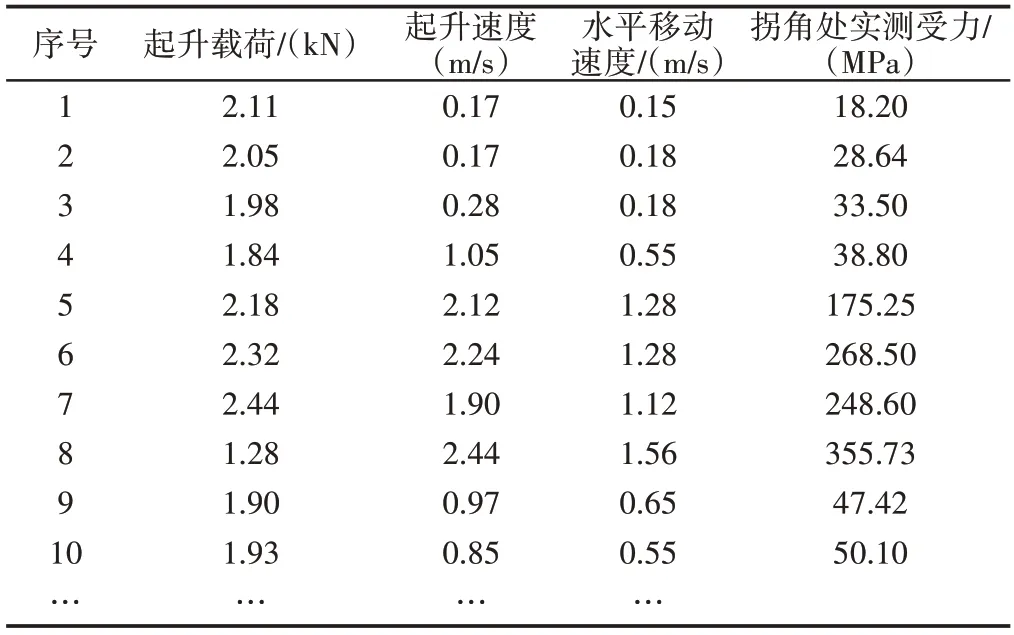
表4 测试数据Tab.4 The Test Data

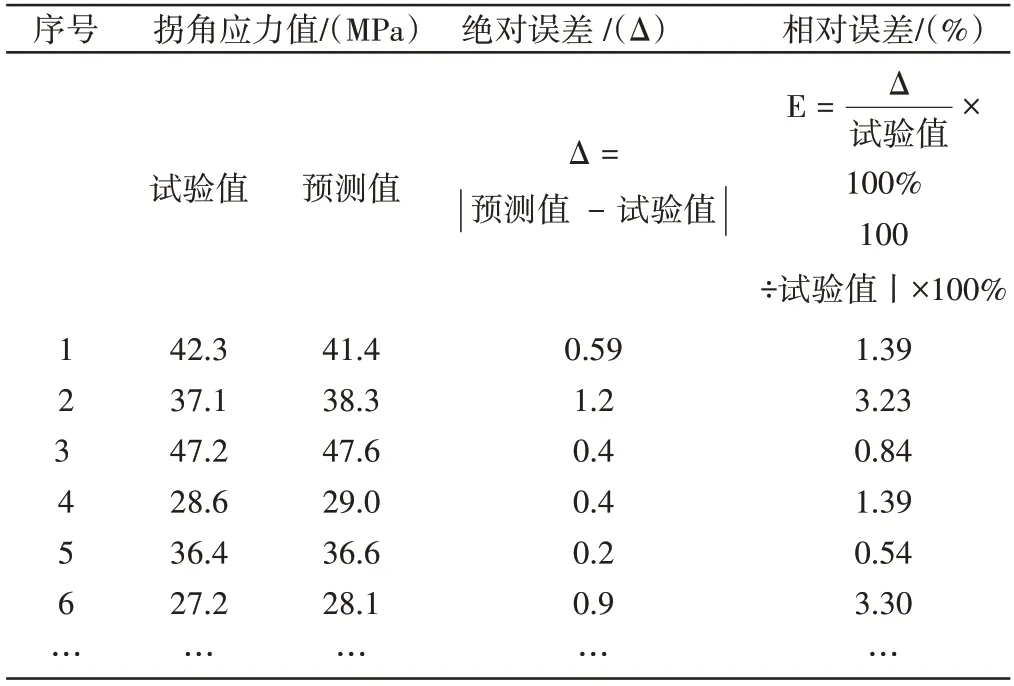
表5 预测值及实际值对比Tab.5 The Comparison Results

运用MATLAB进行对比分析，得出悬臂梁受力实际值和预测值对比图，如图6所示。

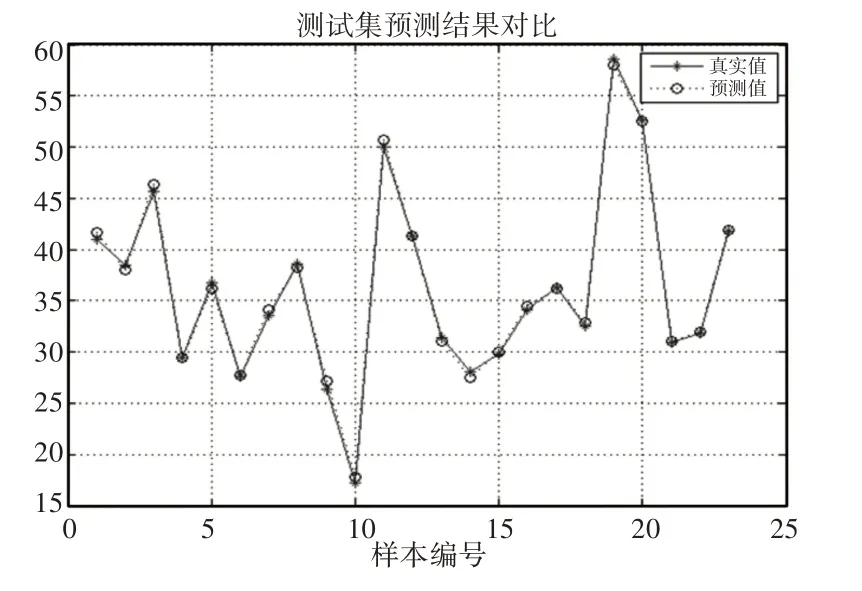
图6 实际值与预测值分布对比图（SVM）Fig.6 Distribution Diagram of Actual and Predicted Values（SVM）

基于分布图可发现，大部分预测点与实测点较为接近，相对误差较小，预测结果比较理想，通过试验验证了该方法的可行性。

4.2 结果分析

选用支持向量机诊断方法构建模型对起重机进行可靠度分析，基于有限元分析结果重点研究悬臂梁尾部拐角处的应力承载情况。通过构建的SVM预测模型预测拐角处应力结果与实测样本进行对比其数据较为接近，通过计算相对误差均在5%以内，考虑到统计学误差10%以内较为合理，因此判定该诊断结果精度较高，方法具有可行性。

5 结论

（1）基于ANSYS创建2t/8.7m壁行式起重机有限元模型，通过静强度分析获取了悬壁梁尾部拐角处是起重机承受应力最为集中的部位，波动范围最为剧烈。（2）选用支持向量机故障诊断方法对起重机受力最恶劣的悬臂梁尾部进行不同工况下的受力预测，通过分析得到影响设备受力的相关特征量，其中起升载荷，起升速度和水平速度通过设计实验进行了获取。（3）构造实验获取测试样本数据，利用MATLAB 工具对支持向量机模型进行训练和验证，通过实测悬臂梁拐角应力值和模型预测值对比，相对误差均在5%以内，预测精度较高，证明了选用支持向量机对起重机可靠度分析方法的可行性。