伺服驱动系统机电耦合动力学特性研究

朱永丽，易 鹏，王晶晶

（1.重庆工程职业技术学院智能制造与交通学院，重庆 402260；2.重庆清研理工汽车检测服务有限公司，重庆 401329）

1 引言

伺服系统是一类包括驱动电机、传动装置、控制系统的机电耦合系统。机电耦合系统的机械耦合参数包括位移、力矩、速度和加速度等，电磁耦合参数包括电压、电流和气隙磁导等[1]。

伺服系统在复杂工况下工作时，由于传动装置刚度较小产生扭转振动会导致驱动电机转子速度产生显著波动。转速波动同样会使得驱动电机电磁场产生扰动，从而使电机绕组中的电流产生振荡，进而引起电磁转矩剧烈振荡。电磁转矩波动又会给系统带来更大的振动。机电耦合振动会导致系统不稳定工作，电机损坏和大规模安全事故。

伺服系统的动态性能会直接影响到产品的加工质量；对系统的动态特性进行分析是提高加工精度的重要基础[2]。文献[3]基于Park变换和磁场Fourier级数理论，建立考虑空间、时间谐波的永磁同步电机非线性数学模型，研究转矩脉动对机电耦合系统扭振特性的影响。文献[4]基于电磁扭矩和转速，驱动电机控制子系统与机械负载子系统构建形成机电耦合关系，分析了永磁直驱系统在多种工况下永磁同步电机输出转速、转矩以及刮板链的速度、加速度等动态特性变化规律，但并未考虑传动装置刚度大小对系统动态特性的影响。

文献[5]通过建立集中式驱动电动车动力传动系统的扭转振动数学模型，提出考虑控制电机动态特性和传动系统的机电耦合仿真方法，并对电机参数进行灵敏度分析，但未考虑传动装置参数变化。

电机和齿轮的运动是一类典型的非线性运动，要准确地分析动态特性，必须要对所建立的模型进行精确求解。文献[6]采用机电系统分析动力学方法推导了机电耦合系统的动力学方程，并应用数值计算方法对耦合的数学模型进行分析。文献[7]基于考虑时变瞬心、刚度的非圆面齿轮动力学模型，采用多阶谐波平衡法求得近似解析解，分析各参数对振动响应的影响规律。

上述分析大多基于双惯量系统进行建模，并用数值方法进行求解。数值方法求解经过一系列的简化过程，所以精确度不如谐波平衡法、多尺度法等解析方法。结合机械动力学、电磁学理论，建立包括电磁刚度的四惯量伺服系统机电耦合模型，采用谐波平衡法进行仿真求解，分析电机电磁刚度这一参数的变化对机电耦合模型的影响，并运用变步长4阶Runge-Kutta数值方法进行验证；从而形成一种机电耦合系统动态特性分析方法，为伺服系统先进控制技术研究提供前提。

2 伺服系统机电耦合系统模型

伺服系统运行过程中，各部件间的运动特性存在多变量耦合关系。传动过程中，由于齿侧间隙、时变刚度等非线性因素存在，会导致齿轮系统出现非线性振动，同时机械振动又与电机的电磁振动相互耦合，将对伺服系统的工作性能和可靠性产生不利影响，如图1所示。

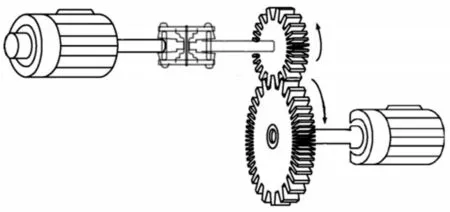
图1 机电耦合模型示意图Fig.1 Schematic Diagram of Electromechanical Coupling Model

2.1 机电耦合模型

通过对电气系统和齿轮传动系统建模并忽略部分参数的影响，可以等效为四惯量机电耦合动力学模型，如图2所示。

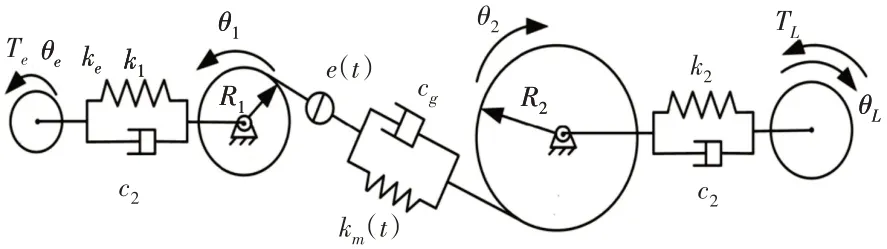
图2 四惯量机电耦合分析模型Fig.2 Four Inertia Electromechanical Coupling Analysis Model

依据胡克定律及动力学分析，四惯量机电耦合系统振动微分方程为：

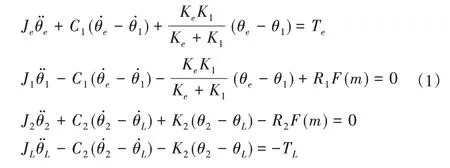
式中：θe—电机转子转角；θ1—主动齿轮转角；θ2—从动齿轮转角；θL—负载转角；Je、J1、J2、JL—电机、主、从动齿轮和负载转动惯量；C1、C2—输入与输出轴扭转阻尼大小；K1、K2—输入和输出轴扭转刚度；Ke—电机电磁刚度；Te、TL—电机电磁转矩和负载转矩；R1、R2—主、从动齿轮基圆半径；F（m）—齿轮动态啮合力。

2.1.1 电机模型

永磁同步电机因结构简单、易于控制等优点广泛应用于精密设备和伺服系统等领域。永磁同步电机通过定子的三相电流产生励磁磁场，定子与转子通过二者之间的磁场耦合，且存在着相对转动。电机的三相绕组具有非线性、耦合强和时变的特点，对其直接进行相应分析困难较大。在电机建模过程中，经常把三相交流绕组等效变换为两相旋转坐标直流绕组，以此简化模型，减少耦合。并做出以下假设：

（1）不考虑磁路饱和以及相关铁芯损耗，各绕组相关参数均为定值；（2）电机三相绕组分布对称；（3）电枢电流为理想正弦电流，且转子不存在阻尼绕组。

基于以上假设得：基于两相旋转坐标系电机模型如下，主要包括电压方程、磁链方程及电磁转矩方程。

定子电压方程为：

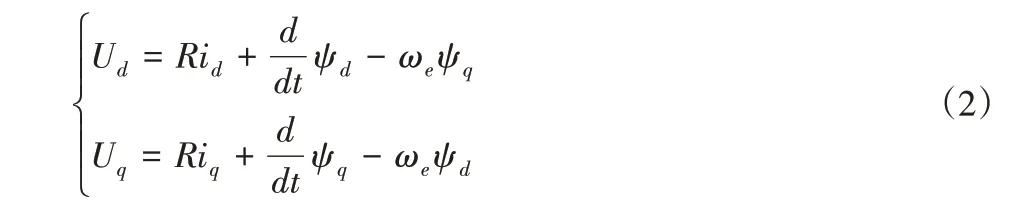
定子磁链方程为：

电机转矩方程为：

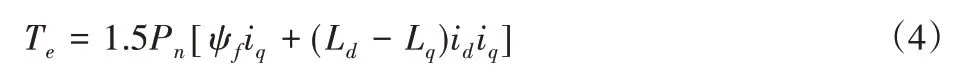
式中：Ud、Uq—定子电压dq轴分量；id、iq—定子电流dq轴分量；R—定子电阻；ψd、ψq—定子磁链dq轴分量；ωe—电角度；Ld、Lq—dq轴电感分量；ψf—永磁体磁链；Pn—磁极对数。

电机运行过程中，定、转子间存在着气隙磁场，转子磁场空间谐波对电机运行特性影响较为明显[8]。因此，驱动电机的电磁刚度、阻尼等电气参数会对机电耦合系统产生较大影响，特别是在如伺服驱动系统这一类精密传动系统建模中应当充分考虑电气参数对机电耦合系统的影响。

电机的定子和转子通过电磁刚度联系在一起，形成一个整体。而电磁刚度由电机特性所决定，对动力系统的动态分析有着重要的影响。电磁刚度定义为电机输出电磁转矩中电转角的一次项系数[9]。电机电磁转矩表达式，如式（4）。所以，电磁刚度表达式为：

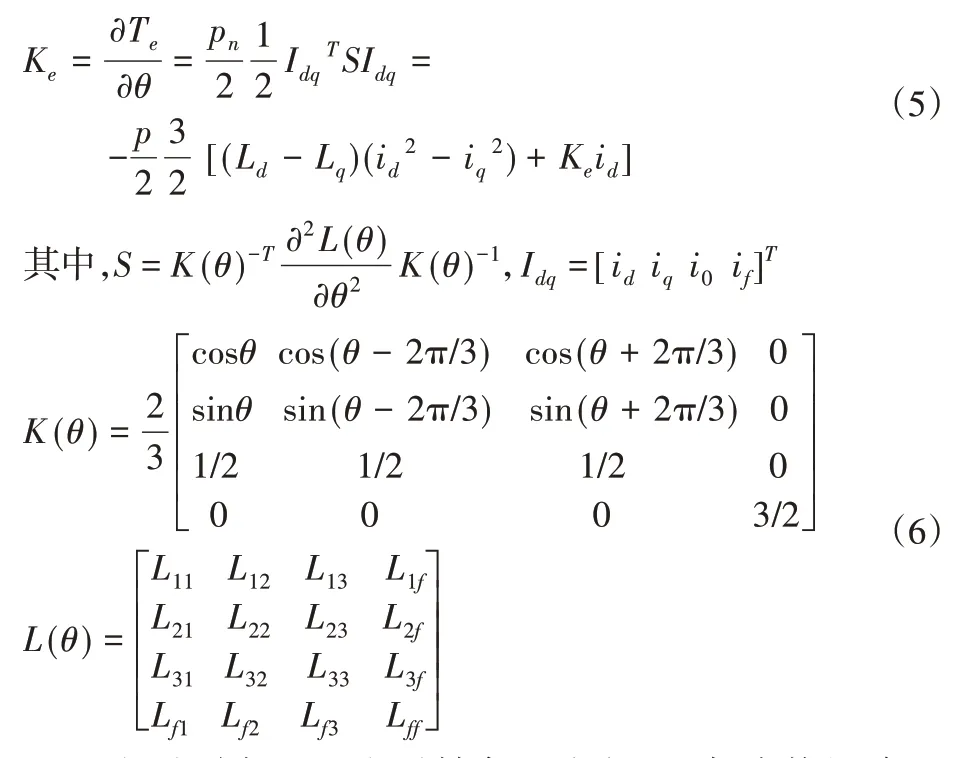
式中：Ke—电磁刚度；θe—电磁转角；C（θe）—坐标变换矩阵；L（θe）—电感矩阵；id、iq、if—dq轴的定子电流和永磁铁的等效励磁电流。

2.1.2 机械系统模型

基于伺服系统运行的特点，只考虑齿轮和轴的扭转振动，不考虑传动轴横向、轴向和支承系统变形。利用集中质量法建立单级齿轮传动扭转振动动力学模型，单级定轴齿轮啮合模型，如图3所示。图3 中：θi（i=1，2）为主、被动齿轮扭转振动位移；Ji（i=1，2）—主、被动齿轮转动惯量；Ri（i=1，2）—主、被动齿轮基圆半径；Cg—齿轮副啮合阻尼；e（t）—齿轮啮合综合误差；Km（t）—齿轮时变啮合刚度。

图3 齿轮传动扭转振动模型Fig.3 Torsional Vibration Model of Gear Transmission

齿轮传动过程中的啮合刚度和啮合误差随时间变化而发生变化。为了准确地分析齿轮传动过程的工作特点，将时变啮合刚度和啮合误差均假设为仅考虑平均值和基频分量的简谐函数。齿轮时变啮合刚度和啮合误差的表达式为：

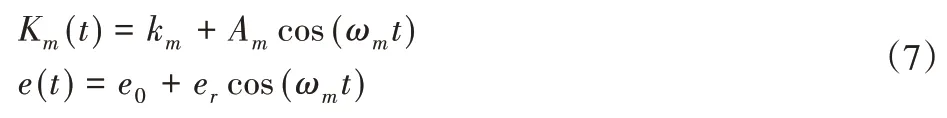
式中：km—平均啮合刚度；Am—时变啮合刚度幅值；ωm—齿轮啮合频率；e0—轮齿误差常量，一般取0；er—齿轮误差幅值。

齿轮的齿侧间隙常常被用来描述轮齿沿啮合线方向的间隙。由于径向间隙的存在，使得中心距发生变化，会导致齿侧间隙的改变［10］。因此，齿侧间隙在齿轮传动过程中并非固定不变，齿侧间隙函数常用分段函数表示。

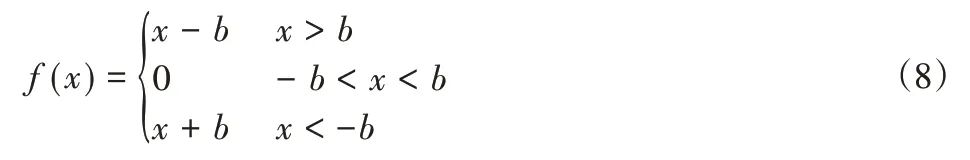
式中：b—齿侧间隙的一半；x—齿轮沿啮合线上相对位移。

齿轮啮合刚度的时变性是由于齿轮齿侧间隙的存在，所以也导致系统输入输出转矩同样会产生波动；故将电磁转矩Te和负载转矩TL也表示为仅考虑定值和基频分量简谐函数。

直齿轮传动时的啮合力Fm主要由齿轮副啮合阻尼引起的粘性啮合力Fc和时变啮合刚度引起的弹性啮合力Fk组成［11］，则动态啮合力的表达式为：

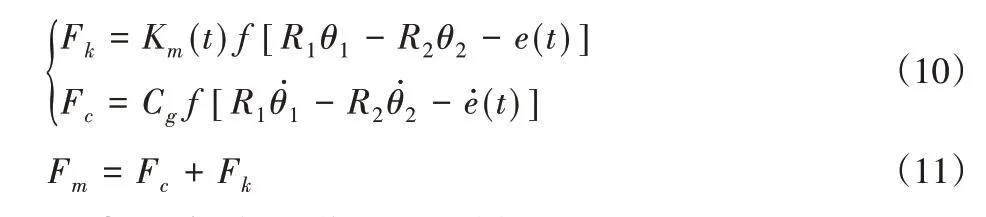
2.2 机电耦合动力学无量纲模型

2.2.1 无量纲模型

伺服系统选用电机为永磁交流伺服电机，传动部分单对直齿轮传动。研究伺服系统机电耦合动力学特性，由于电机、齿轮和负载等模型之间的参数量纲级差别很大，容易导致计算过程中产生误差，并使计算速度变慢。因而，将机电耦合系统中各参数进行无量纲化，进一步加快模型求解速度。选择b—位移量纲标称尺度，τ—时间标称尺度，取广义坐标为：

式中：φ1、φ2—主、从动轴相对扭转角；xp—考虑齿轮啮合误差齿侧变形。

采用等式变换，将齿轮啮合过程中的刚体位移消除，得到四惯量机电耦合模型如下：

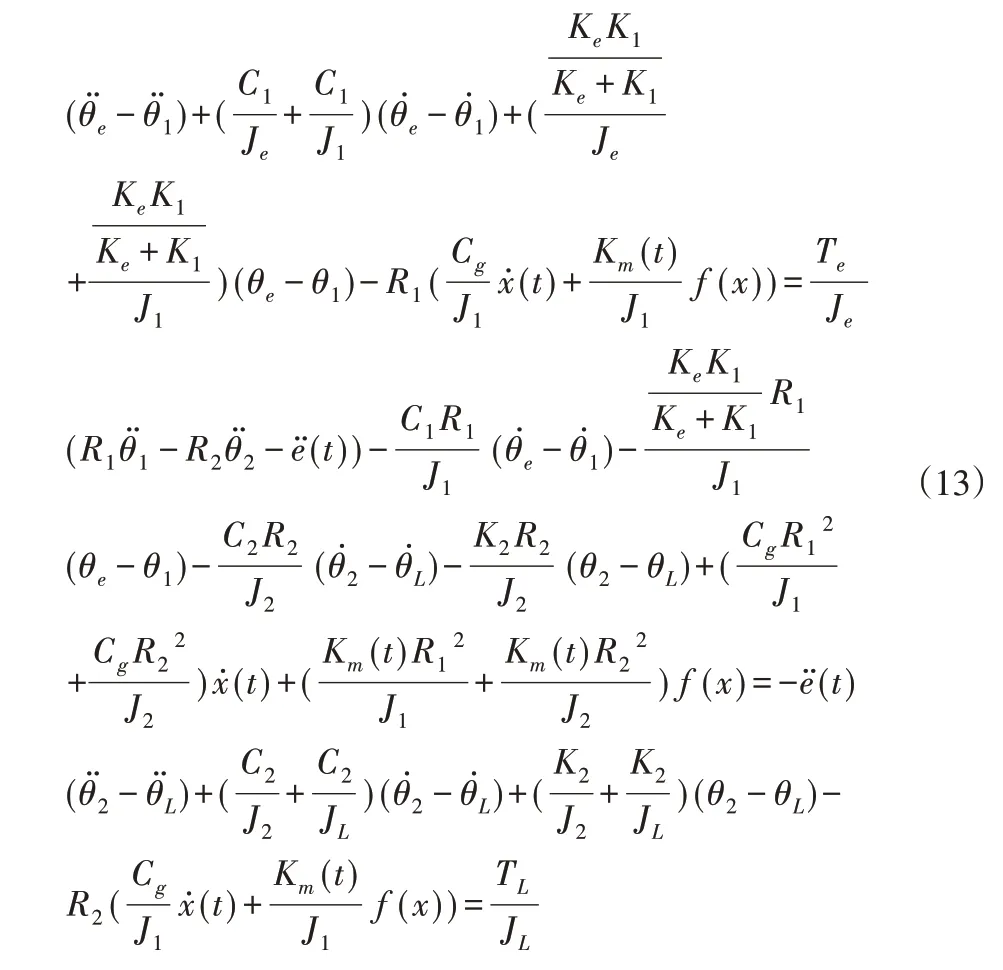
无量纲化之后的物理量如下：

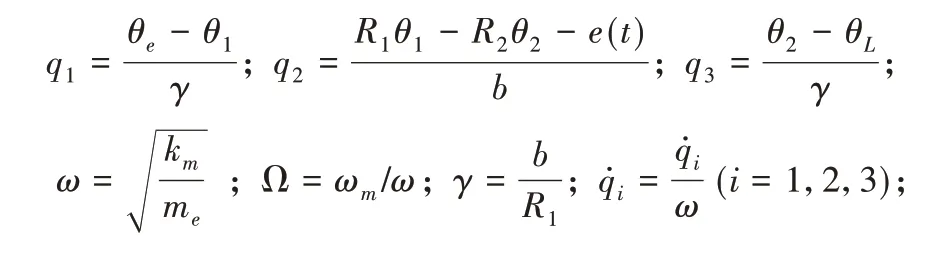
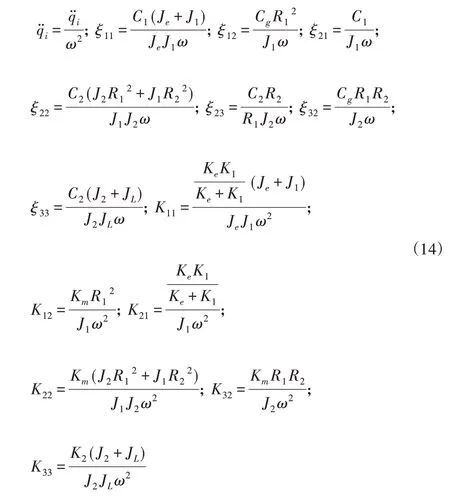
将式（14）代入式（13）并进行化简，得机电耦合振动模型无量纲化模型如下：

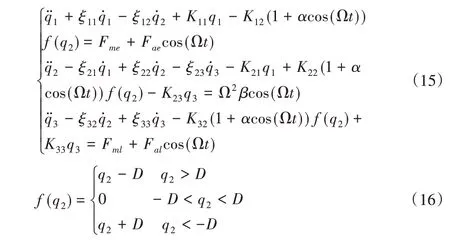
式中：α—刚度波动系数；β—齿轮啮合误差波动系数；Ω—量纲一化啮合频率；f（q2）—量纲一化后的齿侧间隙函数；D—量纲一齿侧间隙值，这里D值—1。

2.2.2 模型参数计算

文献［12］电机转子-齿轮的系统参数选择为：输出扭矩Te为30N·m，负载转矩TL为6N·m；齿轮模数为3mm，齿宽为48mm，齿数为40，齿轮尺侧间隙的一半b=0.1mm；利用石川法计算得齿轮时变啮合刚度的平均值Km=1.2×108N/m。计算得出各部分等效惯量值为：Je=2.8kg·m2、J1=2.6 kg·m2、J2=2.6 kg·m2、JL=2.6 kg·m2。传动轴的扭转刚度为K1=K2=4×105N·m/rad；式（5）、式（6）计算得：电机电磁刚度为105N·m/rad。传动轴阻尼比取0.05，齿轮啮合阻尼比取0.1；传动轴的扭转阻尼C1、C2，齿轮的啮合阻尼Cg分别为：69N·m·s/rad，63N·m·s/rad，137N·m·s/rad。将以上各参数代入至式（14），可得到式（15）中参数取值。

3 增量谐波平衡法

增量谐波平衡法（IHB）是一种将增量过程与谐波平衡过程相结合的方法，对求解强弱非线性系统均适用［13］。采用增量谐波平衡法求解非线性微分方程组时，分为两个过程：增量过程和谐波平衡过程。在增量过程中，先假设微分方程一个解析解的形式，并将其邻域解一同表示出来，代入微分方程组中，从而得到增量方程；其次在谐波平衡过程中，设微分方程解及其增量解均包含谐波项，并代入微分方程组中，且使方程两边具有相同谐波项系数。

令时间尺度τ=Ωt，式中“″”表示为τ的导数，则式（15）可写为：

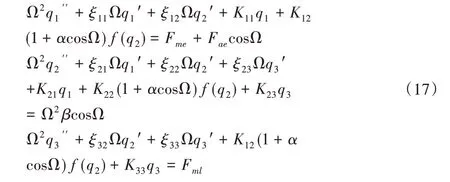
第一步：增量过程。将上式（17）的解设为：

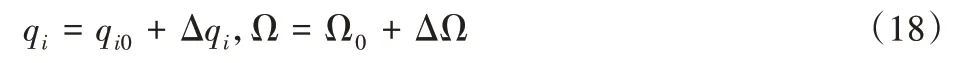
式中：qi0—式（17）的近似解；Δqi—增量方程。i=1，2，3，…，N。

式（17）的高阶近似解和增量方程可写为：

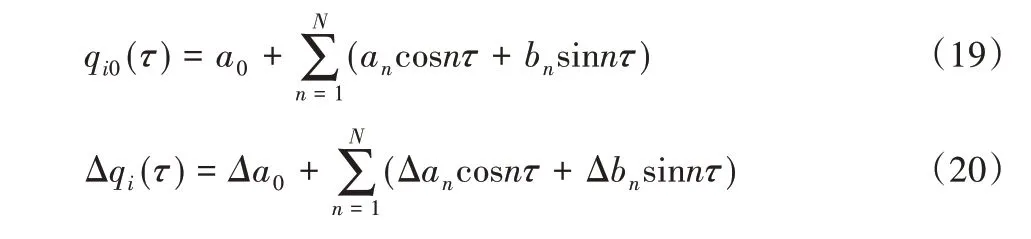
将式（18）代入至式（17）中使用泰勒级数展开，并略去高阶项得到相应增量表达式。

令：

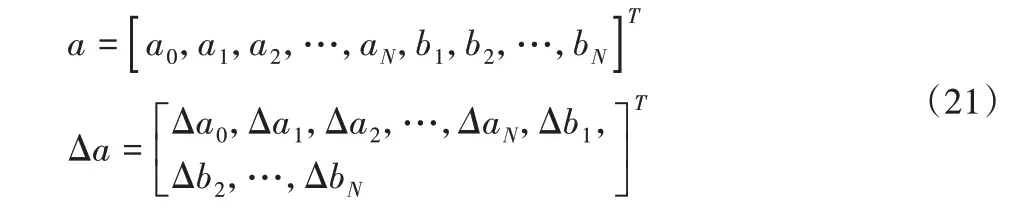
式中：a0—基波幅值；an、bn—高阶谐波幅值；N—所取谐波项，为保证计算的精确度，N取为5。

第二步：谐波平衡过程。采用Galerkin法，将式（21）的左右两边同时乘于cos（iτ）、sin（iτ）（i=0，1，2，…，N），且对其在［0，2π］间进行积分，从而得到如下关于Δa的2N+1阶方程组：

式中：C—2N+1阶矩阵；R—2N+1阶列向量。式（22）为使用增量谐波平衡法得出以Δa为未知数的齿轮系统传动过程中稳态周期响应的计算公式，进行迭代计算，直到满足收敛准则，就可得到所需求解方程组的解。

4 机电耦合系统动力学特性分析

4.1 电磁刚度对系统周期解类型的影响

在工作过程中，伺服电机电转角会发生改变，而电磁刚度为电转角的一次项系数，所以电磁刚度数值也会随之变化。通过选取不同电磁刚度数值，模拟伺服电机的运行过程，从而对系统机电耦合动力学特性进行研究。

电磁刚度分别取值104N·m/rad、105N·m/rad、106N·m/rad，运用增量谐波平衡法和数值解法对模型进行求解；得出伺服驱动系统在不同电磁刚度下的动力学特性。采用增量谐波平衡法取5个谐波项所得到的相图，与数值解法所得出的结果一致，如图4所示。由相图和时间历程图可知：当电磁刚度从105N·m/rad 减小至104N·m/rad 时，系统的周期解始终为一个封闭的圆形，其类型没有发生明显改变；且二者的时间历程图没有较大波动，说明此时电磁刚度对系统的运动状态基本没有影响。当电磁刚度增大至106N·m/rad 时，系统的周期解不再为一个封闭的圆形，而是呈现出一种杂乱无章的封闭曲线，时间历程图也不再是一条周期性曲线，同时波动也显著变大。说明电磁刚度增加至106N·m/rad 的过程中，系统由稳定的周期解运动转变至无序的混沌运动，此时伺服系统处于危险运行的状态。因此，适当增大电机电磁刚度会对系统特性有益，但过分增大电磁刚度会对系统的运行带来很大危害。

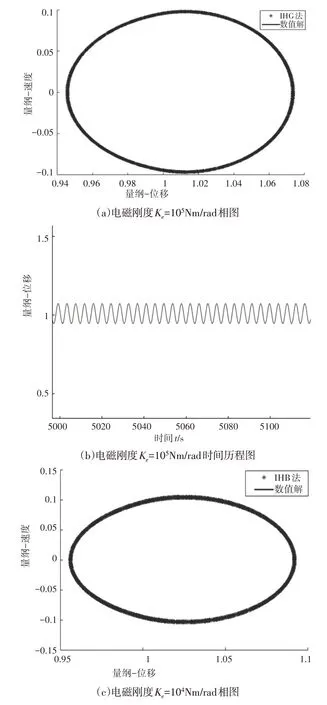
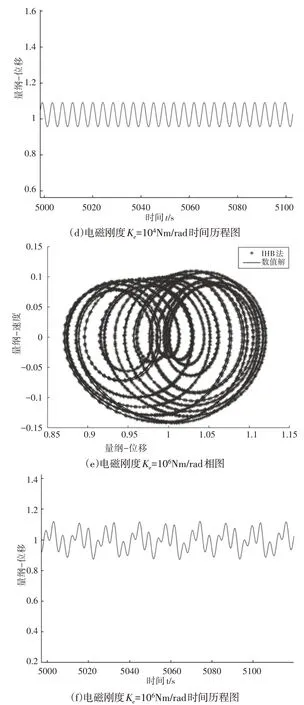
图4 电磁刚度对系统周期解的影响Fig.4 Effect of Electromagnetic Stiffness on Periodic Solution of the System

4.2 电磁刚度对系统幅频响应的影响

由于数值解法的局限性，并不能较为直观对系统的幅频响应进行分析，所以这里同样应用增量谐波平衡法绘制不同电磁刚度Ke下，系统的幅频响应曲线。

电磁刚度Ke=105N·m/rad幅频特性曲线，如图5（a）所示。其起始振动幅值为1.05，最大振幅在1.12以上；电磁刚度Ke=104N·m/rad 幅频特性曲线，如图5（b）所示。相较于电磁刚度为105N·m/rad，起始幅值和振动的最大幅值有一定程度的增大，说明电磁刚度的取值对系统的振动有一定的影响。为电磁刚度Ke=106N·m/rad幅频特性曲线，如图5（c）所示。和电磁刚度为105N·m/rad相比较，起始幅值和振动的最大幅值有一定程度上的降低，说明电磁刚度的增大会使得系统的振动幅值得到抑制；但结合系统的相图和时间历程曲线可知：过分增大电磁刚度同样会对系统安全运行不利。

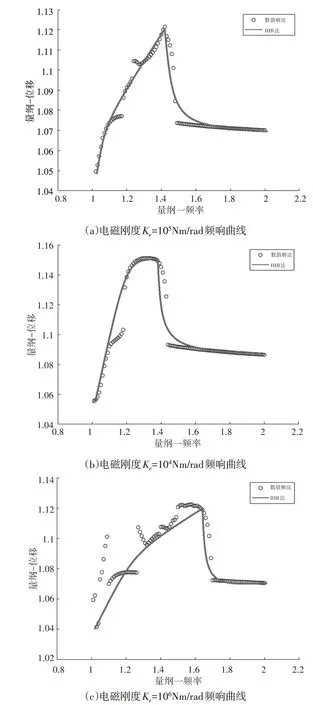
图5 电磁刚度对系统幅频响应的影响Fig.5 Effect of Electromagnetic Stiffness on the Amplitude-Frequency Response of the System

5 结论

伺服电机电磁刚度、齿轮时变啮合刚度会因非线性振动机理复杂，导致机械与电气之间匹配十分困难，在很大程度上制约着伺服系统向高精度方向发展。这里针对这一问题展开分析，得出主要结论如下：

（1）应用增量谐波平衡法对考虑电磁刚度和齿轮啮合振动四惯量机电耦合模型进行求解；由相对扭转位移随电磁刚度变化的时间历程图、相平面图得出：电磁刚度取值不同会使得机电耦合系统出现多周期运动甚至是混沌运动，对系统安全运行造成损害。

（2）电磁刚度对系统的幅频响应有一定的影响。当电磁刚度Ke=104Nm/rad 时，系统的量纲振动幅值增大约0.1；当电磁刚度Ke=105Nm/rad 时，系统的量纲振动幅值增大约0.08；当电磁刚度Ke=106Nm/rad 时，系统量纲振动幅值增大约0.07。因此，电磁刚度的取值应得到一定重视，在工程应用上可以合理选择这一参数。