车内挥发性有机物治理性价比仿真分析研究*

郭秋彦 冯书耀 刘 伟 汪海丰 马 秋 朱振宇 王 雷 刘雪峰

(1.吉利汽车研究院(宁波)有限公司，浙江 宁波 315000；2.中汽数据有限公司，天津 300300)

目前，车辆座舱已成为人们日常生活的第三空间，车内空气质量对驾乘人员的身体健康具有显著影响[1-3]。车内空气中的主要污染物有苯、甲苯、乙苯、二甲苯、苯乙烯、甲醛、乙醛、丙烯醛(以下称五苯三醛)，均属于挥发性有机物(VOCs)，为改善车内VOCs污染，目前的治理手段有采用低VOCs含量的内饰材料、材料通风或应用空气净化除味剂除醛剂等。然而，不同治理方案的治理效果及性价比仍难以定量评估，主要体现在两个方面：一是高性价比治理方案的筛选确定需要以大量的实验测试为基础，成本较高；二是较难通过实验测试多种治理方案之间的相互促进、抑制、抵消等效果。为了解决上述车内VOCs治理方案预期效果定量评价的难题，汽车行业迫切需要一套可靠性较高的车内空气质量仿真分析技术。

近年来，有较多学者尝试对车内空气质量进行仿真研究，TONG等[4]基于质量守恒定律和亨利定律构建了多内饰共存的VOCs稳态散发仿真模型，并用22种内饰模拟总装测试来验证仿真效果，发现五苯三醛的仿真相对偏差为-28.9%～50.0%，准确度较低；WANG等[5]通过30 L小舱测试，证实了用于表征室内建材VOCs散发性能的3个关键散发参数，分别为初始可散发浓度、扩散系数和分配系数，这3个参数同样也适用于表征座椅、顶棚、地毯等汽车内饰零部件的VOCs散发性能。

分析已有文献可知，现有的车内、室内、飞机舱内等密闭空间空气质量仿真研究多停留在均质化单一样品关键散发参数的测算和应用上，即使有非均质多样品共存的VOCs散发研究，也是将散发空间中的VOCs浓度分布简化为混合均匀状态，没有考虑实际无空气对流、VOCs浓度分布不均匀情况下多个样品相对空间位置对VOCs散发的影响，因此无法满足车内VOCs治理预期效果的定量评价要求。为此，本研究在质量守恒定律、亨利定律、菲克第二扩散定律的基础上，利用有限元分析技术构建从单一内饰到总装内饰的多级VOCs散发仿真模型，着力解决多内饰总装状态下VOCs散发浓度的高准确度瞬态仿真问题，为车内VOCs治理方案预期效果的定量评价提供比较可靠的解决思路。

1 研究方法

1.1 VOCs散发方程推导及实测

1.1.1 VOCs散发方程推导

非金属内饰零部件在密闭空间中动态散发VOCs至平衡态后，由质量守恒定律和亨利定律可得式(1)：

Ca1×Va1+Ca1×K×Vm=Cm0×Vm

(1)

式中：Ca1为密闭空间中VOCs的质量浓度，μg/m3；Va1为密闭空间中的空气体积，m3；K为内饰零部件固气界面上VOCs的分配系数；Vm为内饰零部件的体积，m3；Cm0为内饰零部件VOCs的初始可散发质量浓度，μg/m3。

假设该密闭空间中注入一定VOCs后，再次动态散发VOCs至平衡态，由质量守恒定律和亨利定律可得式(2)：

Ca2×Va2+Ca2×K×Vm=Cm0×Vm+M

(2)

式中：Ca2为注入VOCs后密闭空间中的VOCs质量浓度，μg/m3；Va2为注入一定VOCs密闭空间中的空气体积，m3；M为向密闭空间中注入的VOCs质量，μg。

由式(1)、式(2)整理后可得：

(3)

通过实验测试得到M、Ca1、Va1、Ca2、Va2(鉴于注入的VOCs体积较少，引起的体积变化可忽略，即Va2=Va1)、Vm后，代入式(3)即可计算得到分配系数K，再将各参数值代入式(1)，即可计算得到Cm0。

在内饰零部件的密闭空间动态散发过程中，测定多个时间点t处的密闭空间中VOCs质量浓度，连同计算得到的K、Cm0代入C-history公式[6]中，拟合得到内饰零部件中VOCs的扩散系数(D，m2/s)。

1.1.2 基于VOCs散发方程的实验设计

为测算VOCs散发方程中的关键参数，设计单独零部件的密闭空间动态散发及加注VOCs实验；为验证VOCs仿真模型的模拟准确度，设计含12种内饰的模拟总装内饰密闭空间动态散发实验，包括地毯、前座椅、后座椅、仪表板、副仪表板、衣帽架、顶棚、门内饰板、侧围、密封条、方向盘、阻尼板，每种内饰样品取两份。第1份样品测量内饰尺寸得到Vm后，分别用低吸附低气体渗透率的干净聚氟乙烯采样袋真空存放；第2份样品分别用聚乙烯(PE)保鲜膜密封存放。两份样品都于室温下避阳光静置48 h以上，使样品内部的VOCs分布均匀。

将第2份样品的PE包装膜去除，参考车内零部件装配的相对位置，快速将12种内饰摆放于1个4 000 L采样袋中形成模拟总装状态，适度抽出袋中空气。

分别向各采样袋中充入一定氮气(即为Va1)，使样品在25 ℃下持续散发96 h，期间参照《车内挥发性有机物和醛酮类物质采样测定方法》(HJ/T 400—2007)采样6～8次分析五苯三醛，每次采样测试完成后，向采样袋中补充氮气以维持恒定的密闭空间空气体积，以96 h的采样测定结果为Ca1。

完成96 h的采样测定后，用微量进样器向第1份样品的采样袋中分别注入分析纯VOCs液体(组成为1 μL苯+1 μL甲苯+1 μL乙苯+1 μL二甲苯+1 μL苯乙烯+2 μL 30%(质量分数)甲醛+2 μL 40%(质量分数)乙醛+1 μL五苯三醛)，根据密度计算得到各VOCs的质量M。使第1份样品再次在25 ℃下静置96 h，然后采样测定各采样袋中VOCs浓度，即为Ca2。

1.2 VOCs散发仿真模型构建

根据整车测试舱中车内VOCs的散发特点，仿真模型基于3项基本假设构建：(1)因高分子降解、氧化等化学反应引起的材料内各VOCs含量变化较慢，可忽略不计，因此车内VOCs含量满足质量守恒定律；(2)各种VOCs的浓度较低，属于极稀气体，因此不同VOCs分子的扩散互不影响，且在固气界面处的浓度满足亨利定律；(3)车内没有宏观气体对流传质，只有气体分子的自由扩散传质，因此在材料内部和散发空间中的VOCs浓度分布都仅受菲克第二扩散定律控制。在此基础上，分别构建单一内饰VOCs散发仿真模型和总装内饰VOCs散发仿真模型。

单一内饰VOCs散发仿真模型以单一内饰的材料厚度、面积、散发空间尺寸等几何参数构建仿真计算域，对域中几何结构进行有限元网格划分。在材料内部和散发空间各网格节点上应用菲克第二扩散定律，在材料与空气的固气界面处应用亨利定律，指定材料内部各网格节点上的VOCs初始值为Cm0，指定散发空间各网格节点上的VOCs初始值为0 μg/m3，以一定时间步长运行仿真模型，计算得到任意散发时间点、任意散发空间位置处某内饰散发出的及内部含有的VOCs。

与单一内饰VOCs散发仿真模型相比，总装内饰VOCs散发仿真模型中包含了多个内饰的几何结构模型及这些内饰之间的相对位置布局信息，将测算到的多个内饰材料或零部件关键散发参数分别指定到各内饰的几何结构模型上，可计算得到任意散发时间点处及任意空间位置处的由所有内饰共同决定的VOCs浓度。同时，通过分析各内饰内部的VOCs平均浓度水平，还可判定各内饰的VOCs散发(源)或吸收(汇)贡献情况。

1.3 VOCs治理方案仿真

1.3.1 VOCs治理方案仿真设计

本研究对汽车企业最常使用的初始可散发浓度治理方案——自然逸散法的治理效果进行仿真分析，该方案一般先使内饰在相对洁净的环境中室温自然或高温加速散发VOCs一段时间，以降低其初始可散发浓度，然后再将该内饰总装到白车身中，从而达到降低车内VOCs的目的。假设内饰所处3 m3空间以外的区域为清洁环境，VOCs恒定为0 μg/m3，散发条件为25 ℃下自然逸散24 h，在此方案下使用单一内饰VOCs散发仿真模型完成内饰的治理，然后将治理结果代入总装内饰VOCs散发仿真模型，分析各内饰单独治理对总装状态下VOCs减量的贡献。

1.3.2 VOCs治理性价比指标

采用式(4)评估VOCs治理方案性价比：

(4)

式中：P为治理方案性价比；C1、C2分别为治理前后散发空间中VOCs的质量浓度，μg/m3；MT为治理方案的成本。

2 仿真分析

2.1 VOCs关键散发参数测算及验证

2.1.1 VOCs关键散发参数测算

因篇幅所限，本研究仅对甲苯监测数据及其治理性价比进行仿真分析，其他几种VOCs的仿真模型架构与甲苯相同，在仿真分析时代入各VOCs相应的初始可散发浓度、扩散系数和分配系数即可。

按照1.1.2节的实验设计开展12种内饰甲苯的密闭空间动态散发测试，结果如表1所示。

根据表1中甲苯测试数据可将12种内饰分为3类：(1)密封条、方向盘和仪表板在48～96 h甲苯浓度变化不大，认为甲苯达到散发平衡，则先使用式(3)计算得到分配系数K，再用式(1)计算得到初始可散发浓度Cm0，最后借助C-history公式计算得到扩散系数D；(2)副仪表板、门内饰板、后座椅、前座椅、顶棚、地毯等内饰零部件96 h后甲苯浓度继续增加，未在96 h内达到散发平衡，则直接借助C-history公式计算得到多组Cm0、D、K，然后基于相同材质的内饰材料K值相近的原则进行筛选，进而选择同组的Cm0、D参数；(3)对于衣帽架、侧围、阻尼板3种甲苯测试数据接近甚至低于分析仪器检测限的内饰零部件，根据经验指定其关键散发参数为Cm0=10.0 mg/m3、D=1.00×10-13m2/s、K=50。在此水平下，认为内饰自身散发的甲苯和吸附外界甲苯的能力都小到忽略不计。通过以上3种方法测算的各内饰的甲苯关键散发参数见表2。

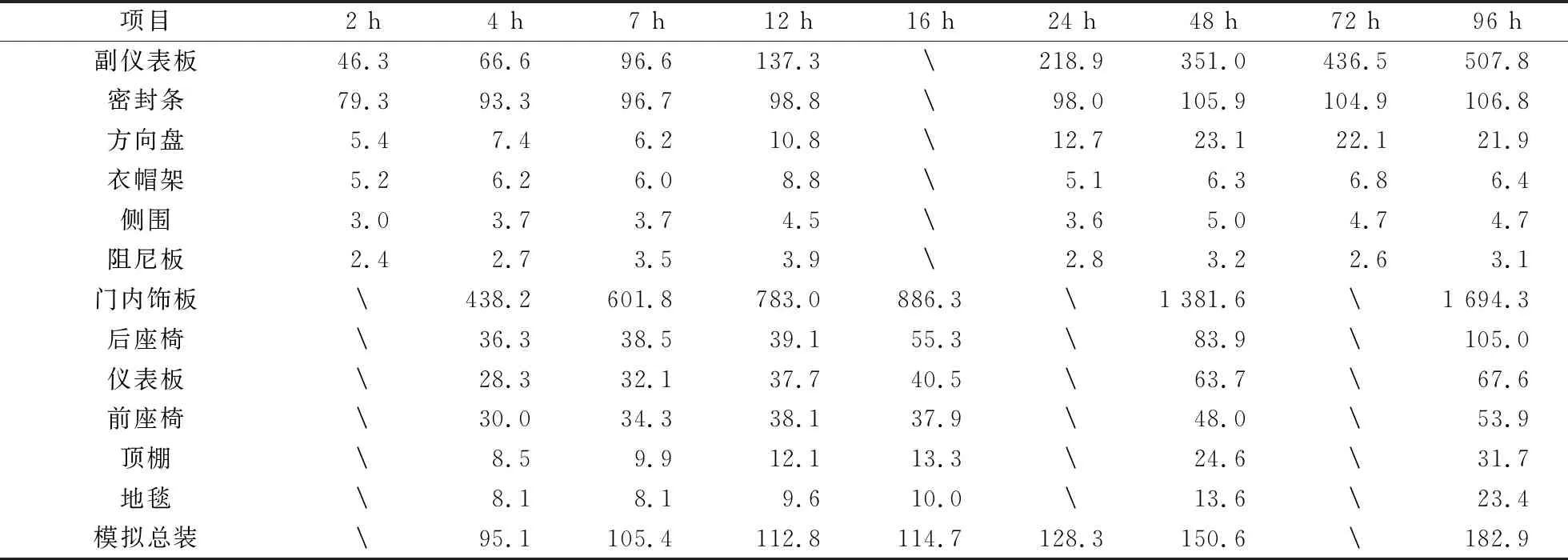
表1 甲苯的密闭空间动态散发测试结果1)

表2 各内饰的甲苯关键散发参数

2.1.2 关键散发参数验证

将某内饰的尺寸数据及其甲苯关键散发参数输入单一内饰VOCs散发仿真模型中，计算得到内饰的甲苯散发情况及其内部的衰减情况，将计算结果与表1中的实测结果进行比较，从而判断测算得到的甲苯关键散发参数的准确性。

以后座椅为例，采用单一内饰VOCs散发仿真模型模拟甲苯浓度随散发时间的变化情况，并与实测值进行对比，结果见图1。可以看出，散发空间甲苯浓度仿真效果较好，与实测值相比平均绝对偏差为4.0 μg/m3，平均相对偏差为9.5%，表明表2中的关键散发参数准确性较好，可以较好地表征后座椅的甲苯散发性能。

此外，从图1中还可看出随着后座椅不断向散发空间中释放甲苯，其内部含有的甲苯也相应地从12.00 mg/m3逐渐下降到了11.35 mg/m3，为甲苯源内饰。

图1 后座椅甲苯散发仿真曲线

2.2 总装内饰VOCs散发仿真及验证

对照模拟总装内饰测试中使用的各内饰尺寸、数量和相对位置，构建多内饰共存的模拟总装几何模型(见图2)。将表2中各内饰的甲苯关键散发参数分别赋值到模拟总装几何模型中进行仿真计算，仿真得到甲苯浓度随散发时间的变化情况，结果见图3。

1—顶棚；2—副仪表板；3—密封条；4—门内饰板；5—方向盘；6—侧围；7—仪表板；8—地毯；9—前座椅；10—阻尼板；11—后座椅；12—衣帽架

图3 模拟总装内饰散发空间中甲苯仿真及实测值对比

由图3可见，在12种内饰共同参与的总装内饰VOCs散发仿真模型中，甲苯在散发空间内散发浓度的仿真值与甲苯实测值符合较好，平均绝对偏差为10.5 μg/m3，平均相对偏差为8.2%，说明该仿真模型可以较准确地描述包含12种内饰的甲苯实际散发情况，可为后续VOCs治理性价比分析提供可靠保障。

对仿真结果中12种内饰样品内部的甲苯平均浓度变化趋势进行分析，可知门内饰板、副仪表板、后座椅、密封条、顶棚、仪表板等6种内饰内部的甲苯浓度呈下降趋势，即为甲苯源内饰，而其他内饰则为甲苯汇内饰。

2.3 重点内饰VOCs治理仿真及性价比分析

2.3.1 重点内饰VOCs治理仿真

将表2中门内饰板、副仪表板、后座椅、密封条、顶棚、仪表板的关键散发参数分别输入单一内饰VOCs散发仿真模型中，设置散发空间为3 m3、自然逸散24 h、开放边界以外甲苯为0 μg/m3，可计算得到各内饰治理前后的初始可散发浓度，结果如表3所示。

2.3.2 VOCs治理性价比分析

将表3中治理仿真结果和表2中关键散发参数输入总装内饰VOCs散发仿真模型，计算各内饰甲苯初始可散发浓度的降低对模拟总装状态下甲苯浓度的影响，并计算治理方案的性价比。

表3 重点内饰甲苯自然逸散治理前后初始可散发质量浓度仿真结果

基于HJ/T 400—2007规定的散发时长和本研究的实验设计，分别使用仿真模型计算散发16、96 h的甲苯浓度，计算VOCs治理性价比。由于自然逸散24 h治理方案的主要成本来自时间消耗，故令MT=1 d，仿真分析结果如表4所示。

表4 重点内饰VOCs治理性价比

由表4可见，门内饰板的甲苯治理性价比最高，通过在25 ℃下自然逸散治理门内饰板24 h，可使模拟总装散发16、96 h的甲苯质量浓度分别由103、186 μg/m3下降至87、156 μg/m3。因此，若想降低车内甲苯浓度，且拟采用的治理方案为内饰零部件室温自然逸散，则应优先考虑针对门内饰板开展治理。

3 结论与展望

以质量守恒定律、亨利定律、菲克第二扩散定律为基本假设，利用有限元数值分析方法近似还原车辆内饰在现实座舱中的空间分布及散发VOCs的时间跨度，开发单一内饰VOCs散发仿真模型和总装内饰VOCs散发仿真模型。以后座椅为例，单一内饰VOCs散发仿真模型模拟的甲苯仿真值与实测值平均绝对偏差为4.0 μg/m3，平均相对偏差为9.5%，关键散发参数准确性较好。总装内饰VOCs散发仿真模型对甲苯浓度的仿真平均绝对偏差为10.5 μg/m3，平均相对偏差为8.2%。基于总装内饰VOCs散发仿真模型的高准确度仿真结果，可以实现不同VOCs治理方案的定量评估。

本研究构建的模型适用于对单独内饰或整车开展VOCs散发测试仿真，以达到减少实验量、降低管控成本的目的。后续研究将逐步解析车载空调或车身漏气等引起的空气对流、环境温湿度的时程变化及以月为尺度的由材料降解、老化等引起的材料内VOCs初始可散发浓度变化等因素对VOCs仿真的影响，以期进一步开发出能够预测使用过程中车内VOCs散发情况的仿真模型。