轨道几何动静态检测分析
2022-09-22张建程朝阳李颖王凡郝晋斐韩志
张建, 程朝阳, 李颖, 王凡, 郝晋斐, 韩志
(1.中国铁道科学研究院集团有限公司 标准计量研究所, 北京 100081;2.中国铁道科学研究院集团有限公司 基础设施检测研究所, 北京 100081)
0 引言
轨道几何动态检测[1](简称动检)是指通过采用综合检测列车、综合巡检车和轨道检查车等设备, 根据设计和相关技术标准对正常运行条件下的轨道几何参数、轴箱和车体加速度等相关参数进行检测。轨道几何静态检测(简称静检)是指没有列车荷载作用下, 检测轨道几何形位。动静态检测均可通过单点超限幅值和200 m区段轨道不平顺质量指数对轨道几何进行评价。静态检测使用的主要工具是轻型轨道检查小车, 检测内容包括轨距、超高、水平、轨向、高低、正矢、扭曲等轨道形位的内部几何参数, 还包括轨道中线的三维坐标及左右钢轨相对于轨道中心线的高程、水平偏差等轨道的外部几何参数。
轨道检查小车[2]一般逐轨枕输出东北天坐标, 动态高低、轨向依据修规要求输出结果为空间曲线。为进行轨道几何动静态比对, 需要将2种数据处理方法统一到同一种输出结果下。对轨道检查小车逐轨枕输出的东北天坐标对应的里程进行最优化筛选, 将静检的空间坐标和动检的惯性空间曲线统一到固定弦长的高低、轨向弦测。
1 动静态检测原理
1.1 绝对测量型轨道检查小车测量原理
绝对测量型[3](绝对型)轨道检查小车的相似产品很多, 但基本原理和作业模式基本一致(见图1), 利用高精度全站仪后视6~8个CPⅢ(基桩控制网)控制点, 交会可获取全站仪设站处的三维坐标。全站仪可自动捕捉并测量安装于轨道检查小车的棱镜中心点, 结合轨检小车几何参数, 再推算出两股钢轨的平面位置和高程。轨道检查小车作业时逐轨枕进行左右三维坐标测量, 全站仪每次设站的有效距离约为70 m, 一站测量完成后需要重新设站, 再重复上述测量过程。一般设站之间存在搭接步骤, 有2 mm左右误差, 由于搭接及重复设站需要人工干预, 易出现粗大误差, 影响检测精度。
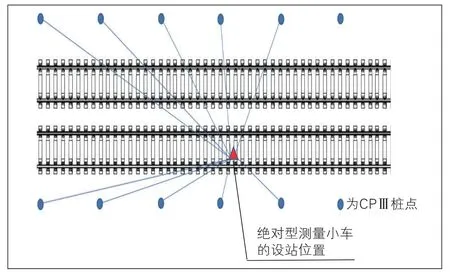
图1 绝对型轨道检查小车测量原理
1.2 相对测量型轨道检查小车测量原理
相对测量型(相对型)轨道检查小车所用的测量技术差异较大, 但几乎都可在动态检测技术中找到其技术根源。目前广泛使用的是陀螺仪轨迹法[4], 原理见图2。通过摇头和点头陀螺仪分别测量轨道的平面偏向角度变化和高度方向的坡度角变化, 利用测量获取的角速率对距离积分得到的轨道空间平面及高程曲线。陀螺仪存在角度随机游走、角速率随机游走、零偏不稳定性等测量噪声[5], 会造成平面偏向角度变化和高程坡度角度变化的测量误差, 对空间距离积分后会进一步影响轨道不平顺的测量精度。目前一般采用引入CPⅢ或GNSS(全球卫星导航系统)进行组合导航测量以抑制惯性测量的精度发散。
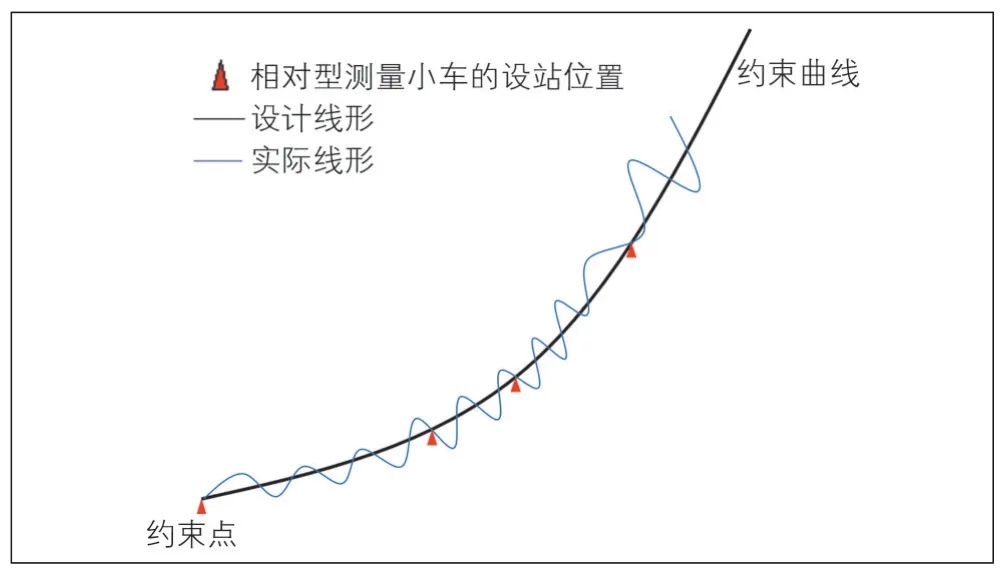
图2 相对型轨道检查小车测量原理
1.3 动态检测原理
动态检测一般基于惯性基准法[6], 原理见图3。
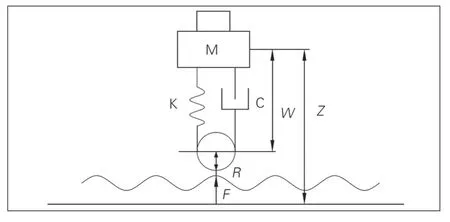
图3 惯性基准法原理
图中:M代表车体, K和C分别为弹簧和阻尼,W为车轮与轮轴的相对位移, 车体相对惯性基准的位移Z为加速度计输出值的二次积分。因轮半径R为常量, 实际测量时公式可修改, 即:
轨道高低不平顺值Y计算如下:
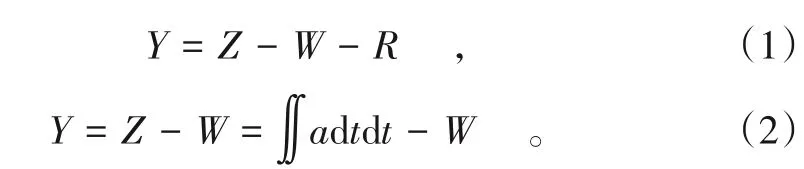
惯性基准法的传递函数恒为1, 为消除坡度高程、坡度变化的影响和长时间的积分漂移[7], 需引入高通滤波器。
2 动静态检测数据
静态检测数据逐轨枕输出钢轨的东北天坐标(e,n,u), 需依据里程将(e,n,u)按照固定弦长2l输出。设弦测法半弦长为l, 弦测法的幅频特性H(λ)及相频特性φ(λ)为:
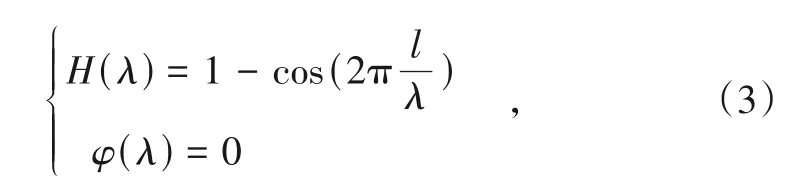
式中:λ为轨道不平顺波长, 式中点弦测法的幅频特性与弦长、不平顺波长有关, 群延迟为零。相频特性没有畸变, 幅频特性随轨道不平顺波长在0~2 mm之间变化, 不同弦长的弦测法幅频特性曲线见图4。
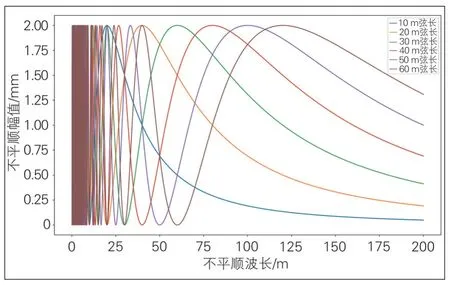
图4 弦测法幅频特性曲线
取波长分别为5、10、100 m, 波幅100 mm的余弦型不平顺作为分析对象, 分别采用10~60 m的中点弦, 弦长步距为10 m, 输出构造单波不平顺[8]的中点弦测值, 模拟得到静态检测不平顺, 得到弦测法对波形扭曲的影响(见图5)。
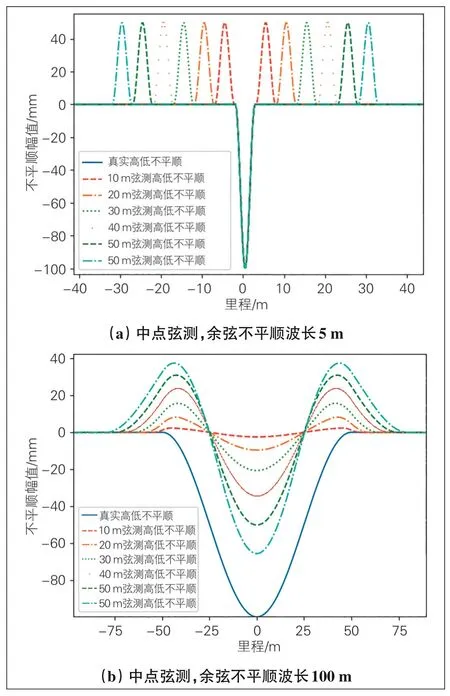
图5 弦测法波形畸变
同一弦长条件下, 不平顺波长小于弦长, 弦测值幅值与不平顺幅值相同;不平顺波长超过弦长, 弦测值幅值小于不平顺幅值;为保证不平顺幅值的精确, 建议采用大于不平顺波长的弦长进行现场测量。
弦测法的输出结果在幅值上存在畸变, 但弦测法的原理及测量方式与人工测量较为接近, 且弦测法的测量结果易与现场复核相结合, 也更易于被现场接受。一般补偿弦测法幅频特性的传递值不唯一, 可采用频率取样法构造逆滤波器[9]对不平顺予以复原。
动检的输出数据以惯性基准为参照(见图6), 引入高通滤波器输出一定波长的轨道不平顺, 同时为满足数据比对的要求, 将基于惯性基准法的空间曲线转化为弦测输出。

图6 惯性基准法
对空间曲线滑动逐次计算各点的弦测值, 即可输出基于惯性基准法的弦测曲线。
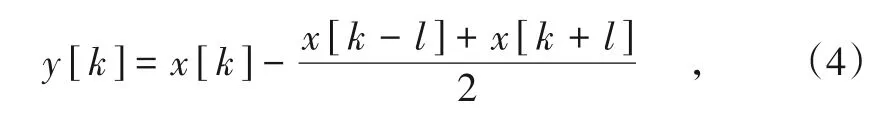
式中:半弦长为l;x[k]为弦中点位置基于惯性基准法的空间曲线不平顺;x[k-l]和x[k+l]为起、终点空间曲线。
3 动静态检测对比分析
动静态检测对比数据源于轨检车和轨检小车同时检测环形铁道试验线路标定Ⅲ线。标定Ⅲ线全长1 km, 最小曲线半径800 m, 设计超高125 mm。试验过程中轨道检查车最高运行速度为80 km/h。
采用轨检小车对K6+400—K7+740、K7+770—K9+000进行静态测量, 其中K6+400—K7+740涵盖无砟和有砟轨道2种结构形式。轨道检查小车采取相对测量方式, 按照里程逐轨枕输出2根钢轨的空间坐标, 实际检测过程中采样点并非恰好位于轨枕的中间位置且轨枕之间也非等间距, 按照轨道检查车的采样间隔0.25 m对数据进行差分。但实际计算中差分易引入误差, 对比效果不好, 故对弦测的坐标点按照里程进行最优化筛选, 选取最符合弦测长度的测点进行弦测滑动计算。
轨道动态检测系统采用编码器并结合专用计数卡进行距离采样[10], 可保证严格按照0.25 m间隔输出, 且整距离采样点数恰等于10、20 m的弦长, 因此相对静态检测里程精度较高。
3.1 高低不平顺动静态数据比对
高低不平顺动静态数据处理流程见图7, 其高低动静态数据10 m弦比对见图8(a), 高低动静态数据20 m弦比对见图8(b)。
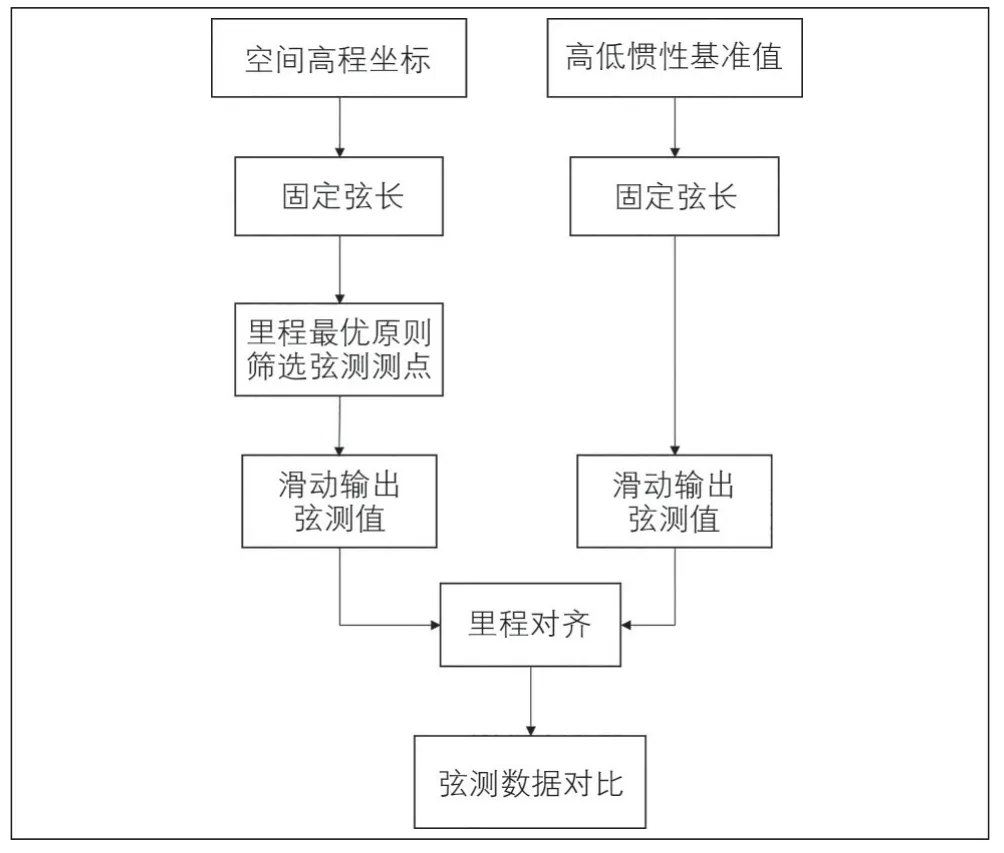
图7 高低不平顺动静态数据处理流程
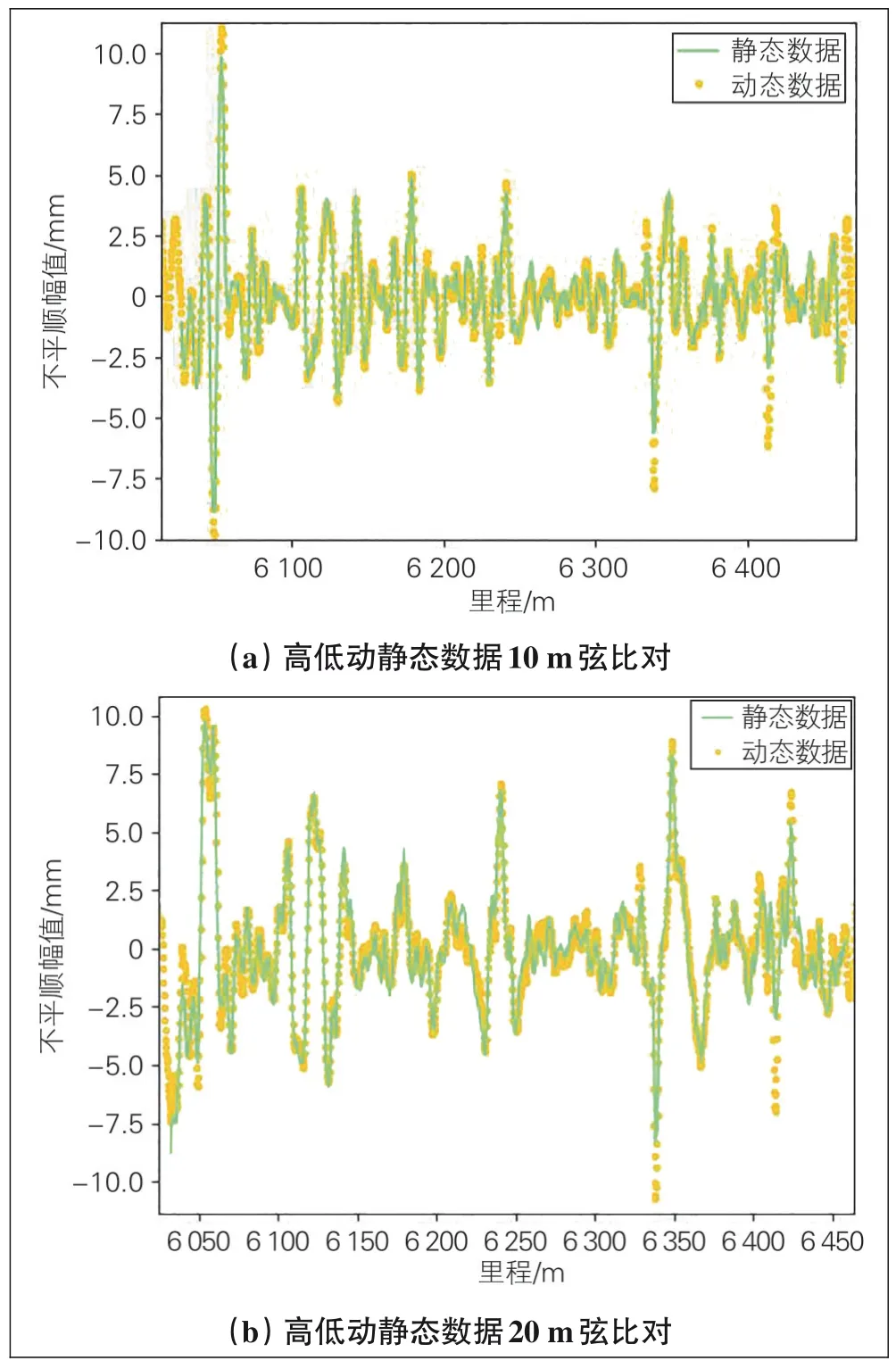
图8 高低动静态数据比对
3.2 轨向动静态数据比对
轨向不平顺动静态数据处理流程见图9, 其轨向10 m弦动静态数据比对见图10(a), 轨向20 m动静态数据比对见图10(b)。
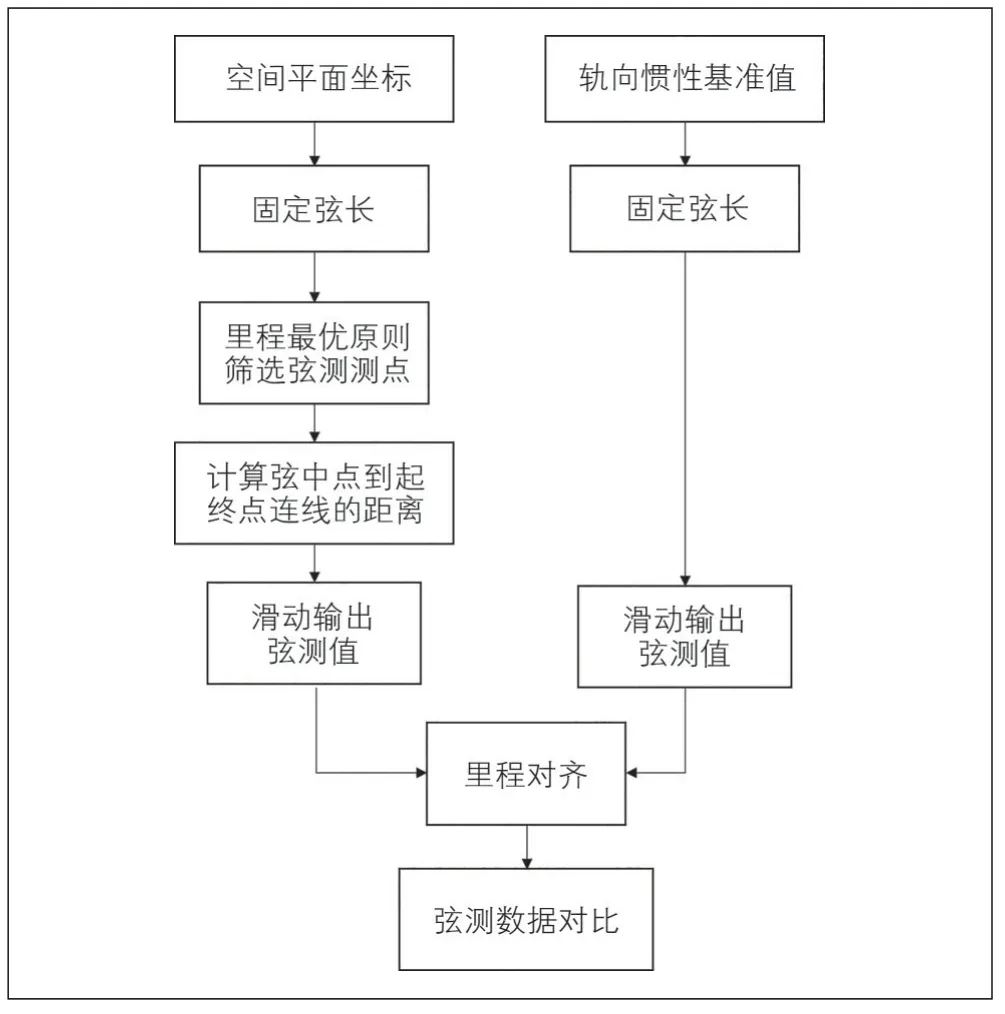
图9 轨向不平顺动静态数据处理流程
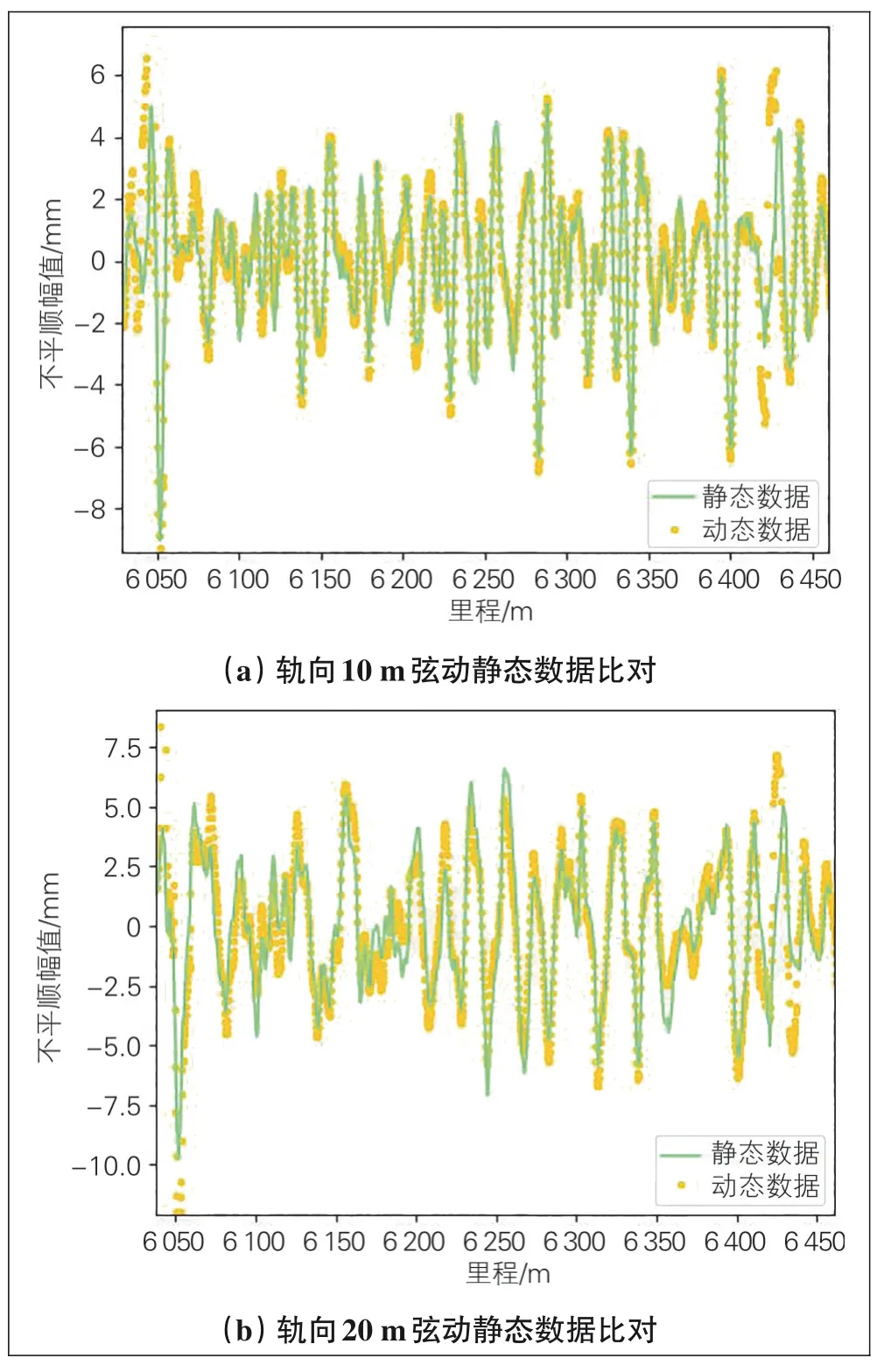
图10 轨向动静态数据比对
动静态结果差值见表1。动静态弦测数据差异较小, 整体重复性较好, 二者左高低、左轨向的10、20 m弦测的偏差值95%分位数小于1 mm。
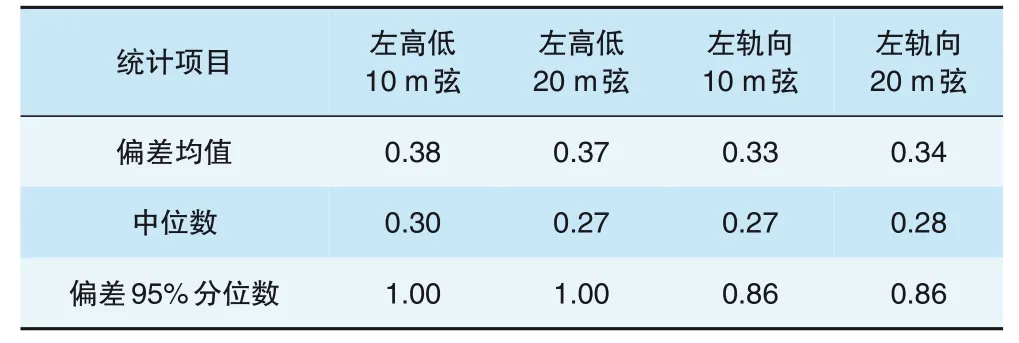
表1 动静态结果差值 mm
4 结论
(1)高低、轨向10、20 m动静态弦测数据对比效果良好, 偏差95%分位数小于1 mm;
(2)弦测法的弦长对轨道不平顺的幅值存在一定影响, 现场弦测时建议选用大于轨道不平顺波长的弦;
(3)动态检测数据速率快, 与静态检测相比无需人工设置测站和检测数据搭接, 粗大误差少;
(4)为更好比对动静态数据, 研究动静态检测数据差异可将静态数据的空间坐标转化为基于惯性基准的空间曲线输出。
