具有高增益低输出电流纹波的Buck-Boost变换器

李梦娇，彭继慎，孙瑄瑨

（辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105）

0 引言

近年来，随着电力电子技术的发展，开关电源逐渐取代线性电源而广泛应用.开关电源在新能源系统的应用也较为广泛，太阳能，燃料电池等新型能源需求高增益、高稳定性的直流电源装置，将其前级较低电压等级的电能(12 V-52 V)转换为并网逆变或直流负载所需求的200 V以上的输入电压，因此研究高增益的直流变换装置具有重要的现实意义.

非隔离 DC-DC变换器具有结构简单控制难度低的优点，其输出电压随着占空比的增加而增加，但是入出电压相差较大的场合，过大的占空比造成变换器电感电流纹波较大，影响变换器性能.提升非隔离型变换器的方案主要有级联升压、倍压单元倍压、耦合电感倍压等[1-4].文献[5]最早提出非隔离耦合倍压方案，通过电感耦合的方式，提升电压增益，可根据不同场合，选择不同的耦合匝比n.但是耦合倍压带来的是模态转换瞬间器件过大的电压冲击.故文献[6]、文献[7]在文献[5]的基础上，通过引入钳位吸收回路，吸收耦合电感漏感能量.在文献[8]～文献[10]中，所提变换器中的钳位吸收回路可通过相互储能的方式，不仅吸收漏感能量，还提升电压增益，这些思路也在文献[10]～文献[14]中有所体现.但是上述文献未分析变换器的输入输出电流纹波特性，文献[15]、文献[16]引入2种零纹波结构，分别实现变换器的低电流纹波输入特性和输出特性，变换器的性能进一步改善.

本文将Buck-Boost变换器的结构进行改进，引入二极管-电容-电感（C-D-L）结构和耦合电感倍压结构，在提高变换器电压增益的同时，通过 C-D-L结构大大减小了变换器输出电流的纹波，实现变换器低输出电流纹波特性.共用 Buck-Boost结构中的C-D支路为无源钳位支路，减小了漏感对变换器电气性能的影响.最后通过搭建150 W的实验样机验证理论分析的正确性.

1 所提变换器拓扑结构

在 Buck-Boost变换器的基础上，通过组合C-D-L结构，得到一种具有零电流纹波输出特性的Buck-Boost变换器结构见图1（a）.电容C1、C2、Co以及输出电感Lo实现了输出电感零电流纹波特性.为提升零纹波 Buck-Boost的电压增益，从理论上来说，增添倍压结构是行之有效的方法，可分为以下方案.

（1）叠加结构方案

叠加结构方案的实质是通过增添一定数量固定结构从而成倍提升变换器的电压增益.图1（b）为叠加电容-二极管-电感（C-D-L-C）结构方案，图1（c）为叠加二极管电容倍增器（diode capacitor multiplier，DCM）结构方案.但是，对于叠加 C-D-L-C结构方案来说，由于叠加单元中存在电感，过多单元的叠加会导致变换器成本与体积增加.而对于叠加DCM结构方案来说，由于DCM结构的特性，在变换器模态转换的瞬间会产生较大的电流冲击，影响变换器的性能.

图1 零纹波Buck-Boost变换器拓扑结构与拓展Fig.1 topological structure and expansion of Buck-Boost converter with output current ripple

（2）耦合电感倍压方案

为了解决叠加结构方案器件过多，较大的电流冲击等问题，通过将耦合电感倍压方案引入所提变换器中，可在不增添过多器件的同时，消除过大的电流脉动，所得拓扑见图2.该变换器在保留低电流纹波输出特性的同时，变换器电压增益可通过匝比n灵活调节，同时将结构中的C1-D1作为钳位吸收结构吸收漏感能量.

图2 所提变换器拓扑结构Fig.2 proposed converter topology

2 变换器工作模态分析

将耦合电感等效为实际变压器模型，折算漏感至一次侧，变换器等效结构见图3.

图3 变换器等效拓扑结构Fig.3 converter equivalent topology

图3中，Lk为折算后的漏感，μH；Lm为励磁电感，μH；原边匝数为Np，副边匝数为Ns，匝；n为匝比（n=Ns/Np）.

当变换器工作在连续导通模式（continuous conduction mode，CCM），变换器各个器件波形与模态回路分别见图4和图5.由于漏感与钳位支路的存在，在一个开关周期内，共有5个模态.

图4 变换器主要波形Fig.4 main waveform of the converter

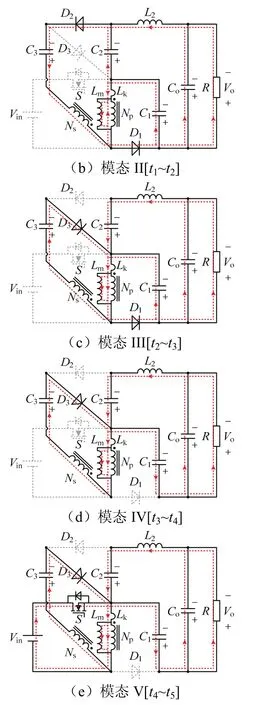
图5 变换器工作模态的等效电路Fig.5 rquivalent circuits of converter working modes

模态 I[t0～t1]：以t0时刻为初始，在此之前开关管S开通，二极管D1和D3截止，D2导通.低压侧电压源持续给耦合电感原边Np储能，漏感电流和励磁电感电流线性上升；副边Ns、电容C3、电源Vin经过开关管S与二极管D3共同给电容C2充电；电容C1给负载供电.

模态II[t1～t2]：开关管S在t1时刻关断，二极管D1快速导通，漏感Lk能量迅速释放，由电容C1快速吸收，漏感电流开始迅速下降，开关管S两端电压被钳位于VC1.同时副边电流受原边的影响也开始减小.当副边电流减小到零时，与其串联的二极管D2自然关断.此模态持续时间非常短，为过渡模态.

模态III[t2～t3]：开关管S处于关断状态，副边电流过零反向增加，二极管D3零电流导通，D1保持导通，D2反向截止.电容C1继续吸收漏感Lk的能量，漏感电流和二极管D1电流继续下降.原边Ns和副边Np经过二极管D3共同给电容C3充电，电容C2能量向负载测释放.当二极管D1电流减小到零时，漏感能量全部释放，吸收二极管D1也随之关断.

工作模态IV[t3～t4]：开关管S保持关断，二极管只有D3导通.电容C3与模态III状态相同，继续由耦合电感结构充电，电容C1和C2共同向负载供电.

工作模态V[t4～t5]：开关管S开通，二极管D3导通.低压侧电源开始给耦合电感原边Np储能，漏感电流迅速上升，受原边电流感应，副边电流开始减小，当副边电流减小到零时，于其串联的二极管D3自然关断.此模态与模态II相同，为过渡模态.

3 变换器性能

3.1 电压增益分析

考虑漏感的影响，耦合系数k与励磁电感Lm、漏感Lk的关系式为

由于模态II和模态V持续时间远小于时间DT和(1-D)T，故在进行分析可忽略.当变换器工作在模态I时，其电压回路见图5（a），有

开关管S关断后，当在变换器工作在模态 III时，其电压回路见图5（c），有

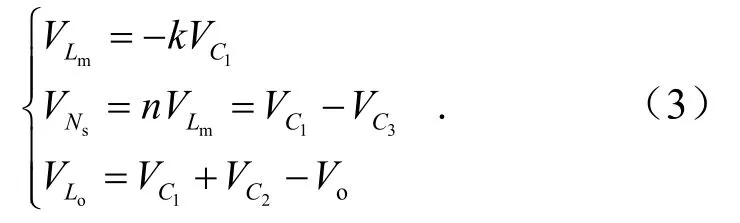
式中，VLm为励磁电感电压；VNs为副边电压；VLo为电感Lo电压；VC1~VC3分别为电容C1~C3的电压；Vin和Vo分别为输入和输出电压.

根据式（1）和式（3），励磁电感Lm的在一个周期内电压积分为零，由此定理可推得电容C1的稳态电压为

同理，根据电感Lo在一个周期内电压积分为0，得

将式（4）代回式（3）得到电容C3的稳态电压为

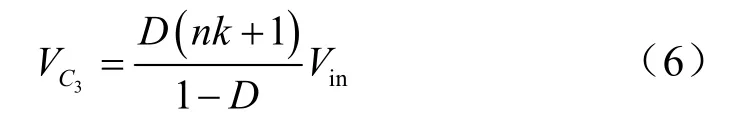
将式（6）和式（4）代回式（1）得到电容C2的稳态电压为

故根据式（5），得到变换器的电压增益为

根据式（8）绘制出在不同匝比n下，变换器的电压增益G三维曲面.由图6电压增益变化曲面看出，匝比n的增加可成倍提升电压增益G.当耦合系数k=1时电压增益最高，k的减小会导致增益损失，磁件制作时可采用双线并绕或者罐型磁芯等方式减小漏感.

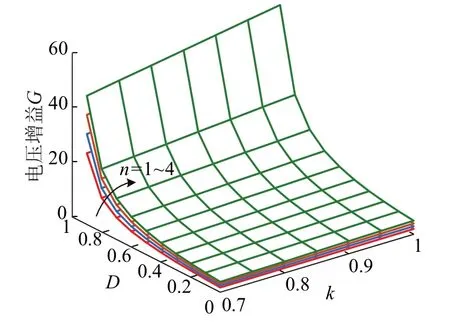
图6 电压增益G的三维曲面Fig.6 three-dimensional surface of voltage gain G

当k=1时，变换器的电压增益为

3.2 电压应力分析

根据3.1节分析，给出各个电容的电压应力分别为

在开关管关断时，其最大电压应力为

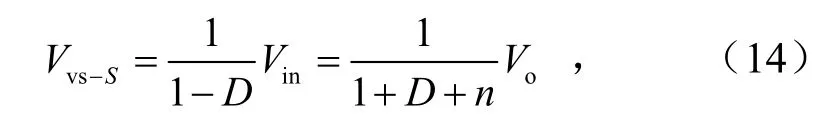
同理，在二极管D1、D2、D3关断时，其最大电压应力分别为

3.3 励磁电感Lm的临界条件

当励磁电感Lm的在开关管S关断后下降并为零，变换器进入断续模态（discontinuous conduction mode，DCM）.断续 DCM 状态会造成电感电流纹波过大，故一半使得变换器工作在连续CCM状态，故需确定最小临界电感值以选择合适电感大小.

对于励磁电感Lm，工作于CCM模式需满足的条件为

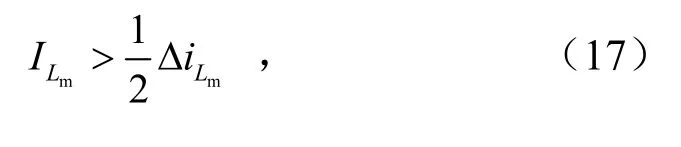
式中，

假设励磁电感Lm很大以至于电流iLm用平均值代替，在此情况下变换器的简化工作波形见图7，其中占空比DxT为二极管D1下降至零的时间.

图7 变换器简化波形Fig.7 converter simplified waveform

由于电容在一个周期内充电电流与放电电流相同，结合工作模态，得到二极管D1、D2、D3的平均电流均等于输出电流Io.由二极管D2可得到占空比为

根据二极管D3，结合式（19）得到励磁电感平均电流

假设励磁电感时间常数为

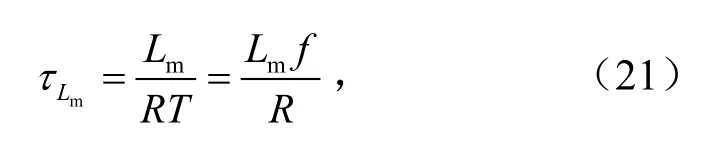
根据式（17）～式（21），得到励磁电感的临界时间常数为

根据式（22），可画出临界时间常数τLmB与匝比n以及占空比D的三维曲面见图8.当τLmB的值位于曲面之上时，变换器选择CCM模式，反之则变换器则选择DCM模式.

图8 变换器CCM/DCM分界曲面Fig.8 Converter CCM/DCM boundary surface

3.4 输出电感Lo电流纹波分析

由于电感Lo位于变换器输出端，其电流纹波直接影响变换器输出端的特性.由于电容在整个开关周期内的电压纹波较小，在模态I~模态V中，电感Lo的电压均可近似表达为

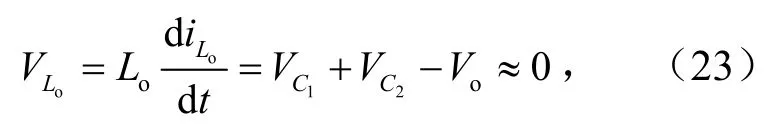
故输出电感Lo在一个周期内电流纹波约为0，变换器具有较低的输出电流纹波.

3.5 变换器性能对比

本文所提变换器与Buck-Boost变换器和文献[18]所提零纹波耦合电感变换器的参数对比，见表1.

表1 不同变换器性能参数Tab.1 different converter performance parameters

在相同占空比D与相同匝比n的情况下，本文所提变换器的电压增益最高，主开关管电压应力也最小.

4 实验结果分析

为验证本文所提具有低输出电流纹波的高增益Buck-Boost变换器原理的正确性，设计了一台输入电压24 V，输出电压200 V，额定功率150 W的实验样机.仿真与实验参数保持一致见表2.

表2 变换器参数Tab.2 converter parameters

利用PSIM仿真软件进行仿真并进行实际样机测试，电压波形见图9.变换器的输出电压为200 V，而根据器件两侧的电压波形，开关管最大电压不到60 V，而各个二极管电压也均小于200 V.将实验波形与仿真波形对比，其电压大小以及变化基本一致.

图9 变换器电压波形Fig.9 converter voltage waveform

变换器各个器件的电流仿真与实验波形对比图见图10.左侧为仿真波形，右侧为实验波形，耦合电感原副边电流波形与理论分析变化方式相同.而二极管D1、D2、D3的变化方式也相同.观察输出电感Lo的波形，可以看出，变换器的输出侧电流脉动非常小.对比仿真与实验波形，其电压大小以及变化基本一致.

图10 变换器电流波形Fig.10 converter current waveform

5 结论

本文将Buck-Boost变换器的结构进行改进，引入耦合电感升压结构，提出了一种具有低输出电流纹波的高增益Buck-Boost变换器，具有以下特点：实现了输出端电感零纹波电流输出特性；引入耦合电感升压结构，变换器的电压增益可通过耦合电感匝比n进行灵活调节；采用无源钳位支路改善变换器的性能，实现开关管低应力和漏感能量的吸收.