基于椭圆重叠区域的蚕茧图像融合方法

孙卫红， 黎 雨， 梁 曼， 邵铁锋， 高明辉

1. 中国计量大学 机电工程学院， 浙江 杭州 310018； 2. 中国计量大学 茧丝绸质量检测技术研究所， 浙江 杭州 310018； 3. 泰安市纺织纤维检验所， 山东 泰安 217000)

蚕茧缫丝之前需先通过选茧工作剔除影响生丝质量的下茧。目前，表面带有疵点的蚕茧一般通过其表面疵点的总面积判断是否为下茧，如靠黄茧、油茧、烂茧、霉茧等。由于人眼无法准确判断疵点面积，且目前的疵点茧检测技术一般只对带有疵点的单一面进行分析[1]，忽略了蚕茧表面其他角度的疵点情况,因此,需通过拍摄不同角度的蚕茧图像后，采用图像拼接处理得到完整的蚕茧表面图像，再对其疵点特征进行分析。

图像拼接技术一般包括特征点提取、图像配准、图像融合等步骤[2]。其中，图像融合是在图像配准的基础上，消除拼接图中因亮度差异等因素造成的拼接缝，获得平滑过渡的融合图像。目前,常用的图像融合算法有加权平均法、渐入渐出算法、多分辨率融合算法与泊松融合等。加权平均法[3]和渐入渐出算法[4]实时性较好，但得到的融合图曝光差异大且存在明显的拼接缝。多分辨率融合算法[5]与泊松融合[6]能有效消除拼接缝，但这2种算法耗时较长且均需掩码图像。针对不同场景的图像需设计相应的融合算法来消除拼接缝，李海超等[7]利用区间差值映射法对图像重叠区域进行直方图匹配并建立直方图查找表，有效消除图像间的灰度差异。瞿中等[8]将最佳缝合线与改进加权平均融合算法结合,生成平滑过渡且无拼接缝的高质量图像。汪丹等[9]提出在渐入渐出算法的基础上，将过渡的权重值替换为三角函数，得到更好的融合效果；但由于蚕茧图像的特殊性，其黑色背景是导致融合图中蚕茧边缘拼接缝明显的主要原因，因此，蚕茧图像融合不似传统意义上的矩形图像融合[10]，而是针对图像中的蚕茧表面区域进行融合。

为获得良好视觉效果的蚕茧完整表面，本文提出一种基于椭圆重叠区域的蚕茧图像融合方法，将图像中蚕茧表面所在区域等效为椭圆带入融合过程，构建蚕茧图像融合的数学模型，将实际融合区域定义为由模型得出的椭圆重叠区域，并采用改进的三角函数权重算法对该区域进行融合。

1 蚕茧图像的采集与配准

由于需获取视觉效果佳且平滑过渡的蚕茧完整表面图像，因此，要求采集的蚕茧图像需在尺寸、亮度与旋转角度方面尽量保持一致。本文采用课题组研制的蚕茧茧层完整图像采集装置[11]获取尺寸、亮度与旋转角度基本相同的蚕茧原始图像，如图1所示。2个滚轴朝同一个方向滚动，每转动60°拍摄1张蚕茧表面图像直至获取完整表面，再选取2张相邻且带有同一疵点的蚕茧图像用于后续处理。蚕茧的形状为类椭球形，导致采集的蚕茧原始图像存在信息压缩，因此，本文通过等效阶梯柱面模型[11]对蚕茧原始图像进行展开，并将展开后的蚕茧图像作为待拼接图像进行后续拼接处理。

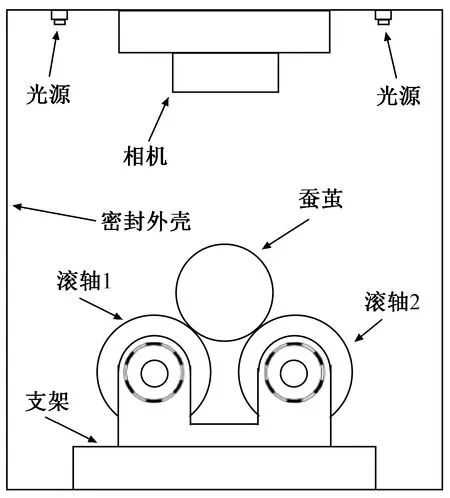
图1 采集装置示意图

蚕茧图像融合之前需先完成图像配准工作，通过寻找2幅图像的空间变换，将蚕茧图像左图映射到蚕茧图像右图上，使2幅图中位于空间同一位置的点对应起来[12]。本文利用SURF算法[13]检测蚕茧图像的特征点，检测完毕后为每个特征点构建64维SURF特征描述子。再采用RANSAC算法寻找2幅蚕茧图像中的最佳单应性矩阵，并筛除误匹配点得到最终匹配对。根据各匹配对之间的距离计算蚕茧图像右图相对于左图的平移距离(dx,dy),如式(1)与(2)所示。

(1)

(2)

式中：N为RANSAC算法筛除后剩下的匹配点总对数；dxn为第n对匹配点在x方向的位移距离；dyn为第n对匹配点在y方向的位移距离。

2 蚕茧等效椭圆的图像融合方法

2.1 蚕茧类椭圆模型

一般蚕茧的形状为类椭球形，因此，其二维图像中的蚕茧表面可等效为椭圆。本文对展开后的蚕茧图像进行灰度化、二值化后，采用直接最小二乘拟合算法[14]对其进行拟合，结果如图2所示。可以看出，展开后的蚕茧类似于标准的椭圆曲线，由此获取等效椭圆的相关参数并映射到原蚕茧图像的像素坐标中。

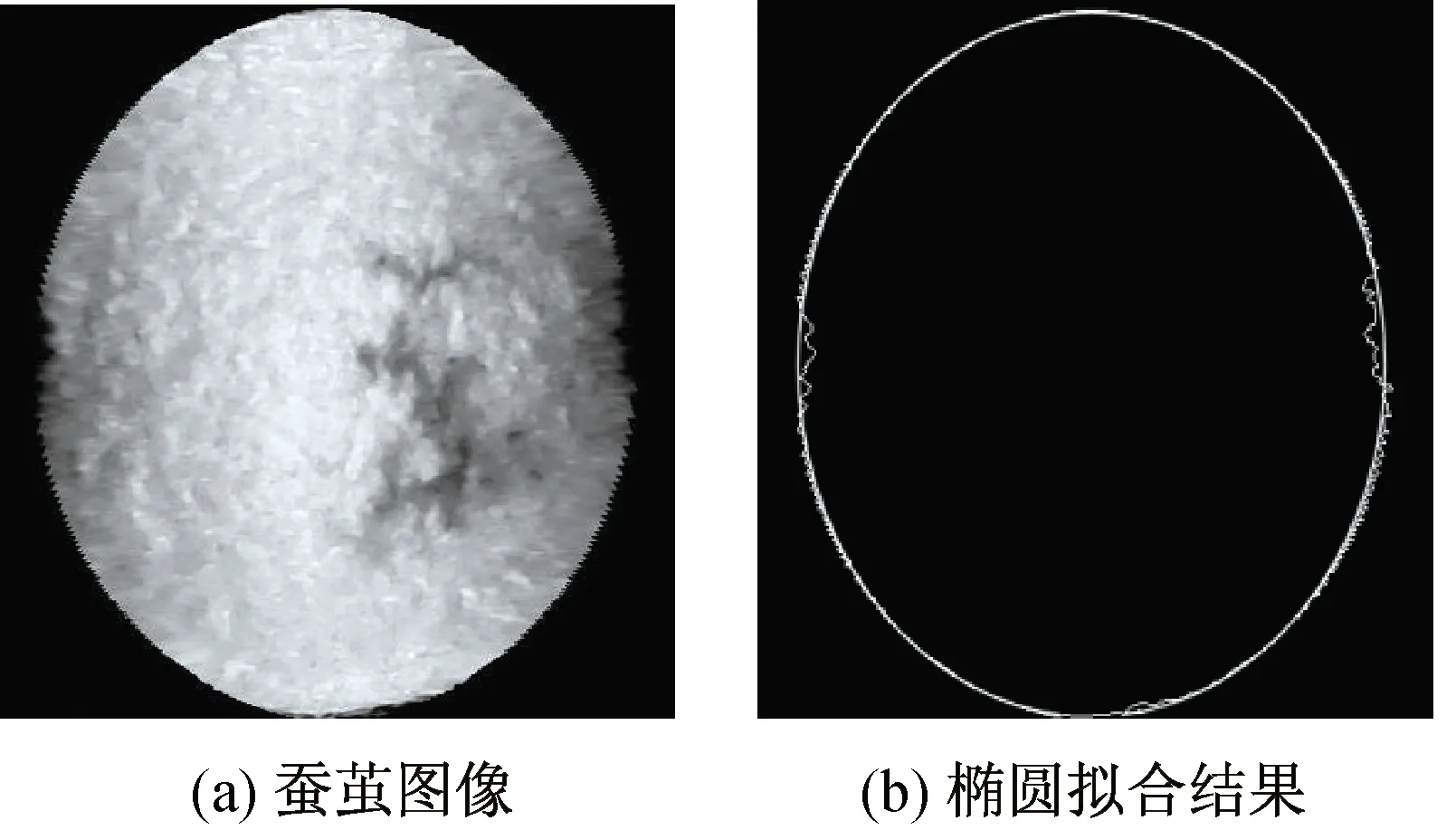
图2 蚕茧图像椭圆拟合

采集装置通过旋转蚕茧来拍摄不同角度的蚕茧原始图像获得蚕茧茧层完整图像，为此认为蚕茧图像左图与蚕茧图像右图中的蚕茧等效椭圆方程相同。定义椭圆的长轴为2a,短轴为2b，圆心在图像中的位置为(xc,yc),即可得到2幅图中的蚕茧表面等效椭圆如式(3)所示。

(3)

2.2 蚕茧图像融合的数学模型

将蚕茧图像的融合区域定义为2个椭圆的重叠区域，而非传统方法中图像实际的矩形重叠区域。为获取融合过程中蚕茧等效椭圆重叠区域的点集，本文根据图像配准过程得到的水平位移距离dx与竖直位移距离dy，构建蚕茧图像融合的数学模型。竖直位移距离dy存在大于、等于和小于0这3种情况，导致蚕茧图像融合的数学模型也存在3种情况，但这3种情况无本质区别，不做过多赘述。以dy<0为例，构建的融合数学模型如图3所示。

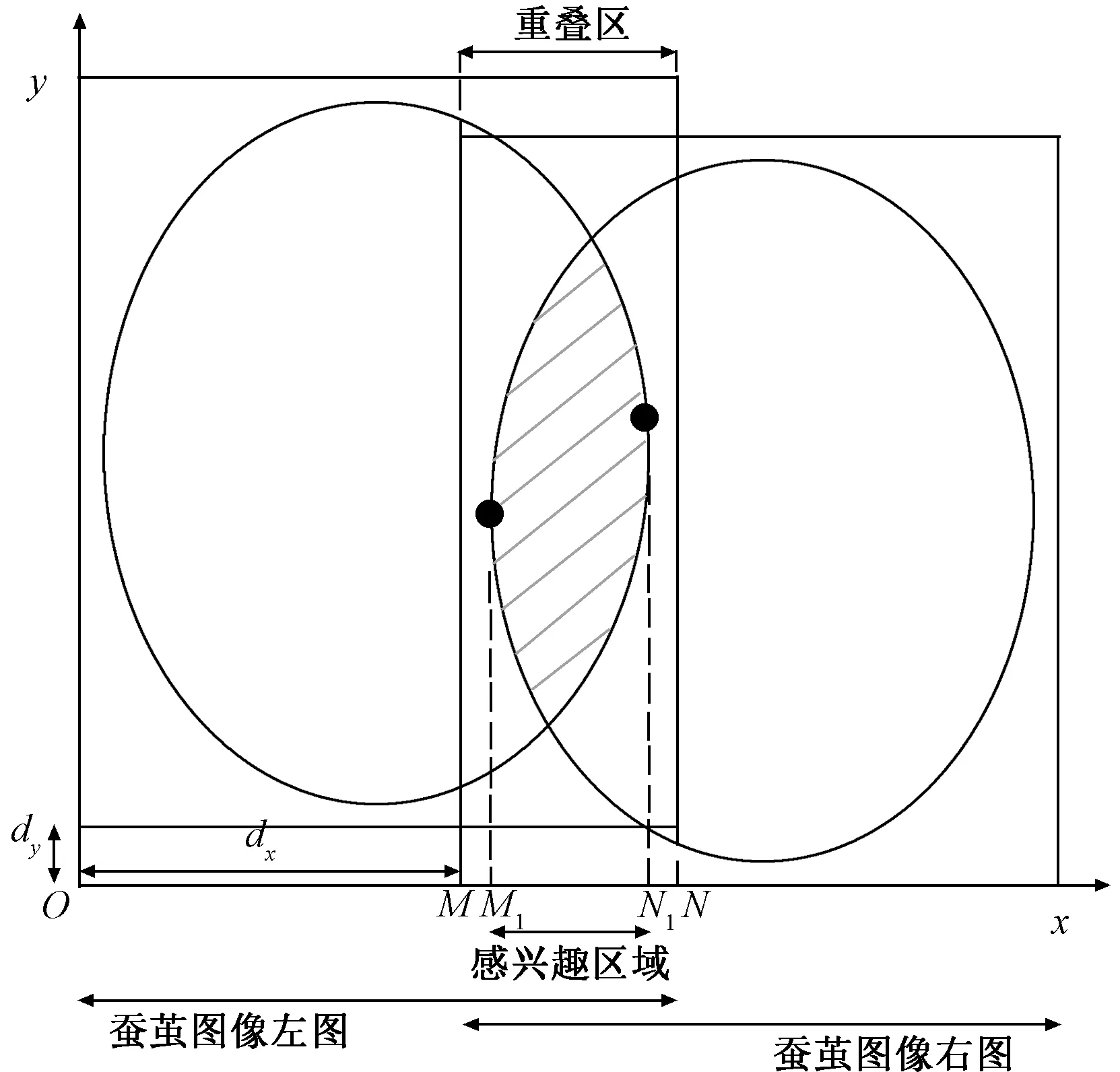
图3 蚕茧图像融合数学模型

设蚕茧图像左图与右图尺寸均为W×H,则蚕茧融合图像的尺寸为(W+dx)×(H+dy)。定义蚕茧图像左图为模板图像，则该图像中的蚕茧等效椭圆相当于向上平移了dy个单位，蚕茧图像右图中的等效椭圆相当于向右平移了W-dx个单位。得到左图中的蚕茧等效椭圆区域为A，右图中椭圆区域为B,因此,2个椭圆重叠区域的点集为C，如式(4)～(6)所示：

(4)

(5)

C=A∩B

(6)

2.3 改进的三角函数权重算法

本文融合算法的基础为耗时较短的三角函数权重算法[9]。三角函数权重算法是对渐入渐出算法的改进，其原理是在图像重叠区域按照式(7)计算每一列与角度的关系，再得出该角度下正、余弦值的平方作为融合权重值。

(7)

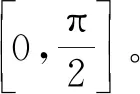
为排除图像中无关因素的影响，改善黑色背景导致亮度不均、蚕茧边界线明显的情况。本文在原有算法基础上，将三角函数权重算法的构建区域由图像实际重叠区域改为感兴趣区域。利用融合数学模型中2个等效椭圆的位置方程，计算得出蚕茧重叠区域的最大宽M1N1，并将其与融合图的高组成的矩形作为感兴趣区域，同时在该区域内计算每列像素与角度θ1的关系如式(8)所示，再按照式(9)、(10)得出该角度下的左图融合权重Q与右图融合权重T,得到改进的三角函数权重算法。

(8)

T=sin2θ1

(9)

Q=cos2θ1

(10)

式中，M1与N1分别表示蚕茧图像中感兴趣区域的左、右边界。

最后，通过式(11)、(12)得到蚕茧融合图像I的像素点与蚕茧图像左图L与右图R之间的关系。感兴趣区域与权重变化如图4所示。

图4 改进的三角函数权重变化图

I(x,y)=Q×L(x,y)+T×R(x,y)

(11)

(x,y)∈C

(12)

对椭圆重叠区域分别采用三角函数权重算法与改进的三角函数权重算法进行融合，结果如图5所示。由于本文进行融合的区域为椭圆的重叠区域，其宽度小于图像的重叠区域，因此，通过三角函数权重算法得到的权重最大值并非为1,使得蚕茧融合图像在椭圆边界处的亮度呈跳跃变化，椭圆边界线清晰可见，无法获得自然过渡的蚕茧表面。但改进的三角函数权重算法将图像重叠区域改为感兴趣区域，使其权重值由0到1连续变化，保证了椭圆边界线区域平滑过渡，得到高质量的蚕茧融合图像。

图5 改进前后三角函数权重算法的融合结果对比图

2.4 图像融合方法描述

图像融合方法主要包括以下步骤。

步骤1：获取2张不同角度的蚕茧原始图像后，对其进行展开处理，得到蚕茧图像作为待拼接图像。

步骤2：利用SURF算法对2张不同角度的蚕茧待拼接图像进行配准，再采用RANSAC算法筛除误匹配对，根据最终匹配对的距离得出蚕茧图像右图相对于左图的移动距离(dx,dy)。

步骤3：采用最小二乘拟合算法分别对2张待拼接图像中的蚕茧表面进行椭圆拟合，并输出其等效椭圆的位置方程。

步骤4：将蚕茧图像左图作为参考图像，根据配准得出的平移距离(dx,dy)对右图进行平移，得到蚕茧图像融合的数学模型，由此获取2个等效椭圆重叠区域的点集。

步骤5：根据2个等效椭圆在蚕茧融合图像中的位置方程，得出椭圆重叠区域的最大宽M1N1,并将M1N1所在区域作为感兴趣区域。

步骤6：在感兴趣区域内利用改进的三角函数权重算法进行融合处理，得到自然平滑的蚕茧融合图像。

3 实验结果与分析

图像融合评价方法一般分为主观评价与客观评价。主观评价主要依靠人眼评价融合图像的质量，客观评价通过某种特定算法来提供量化的评价值[15-16]。为确保本文方法的有效性与准确性，同时采用主观评价与客观评价来评估蚕茧融合图像质量。

3.1 蚕茧图像融合质量主观评估

蚕茧图像融合试验平台是CPU为2.4 GHz，内存为4GB，操作系统为Windows10计算机，软件平台由Visual Studio 2017和Opencv2.4.9组成。选取图6所示的2组表面特征不同的蚕茧图像，分别采用渐入渐出算法、三角函数权重算法与本文基于椭圆重叠区域的蚕茧图像融合方法进行融合，结果如图7、8所示。

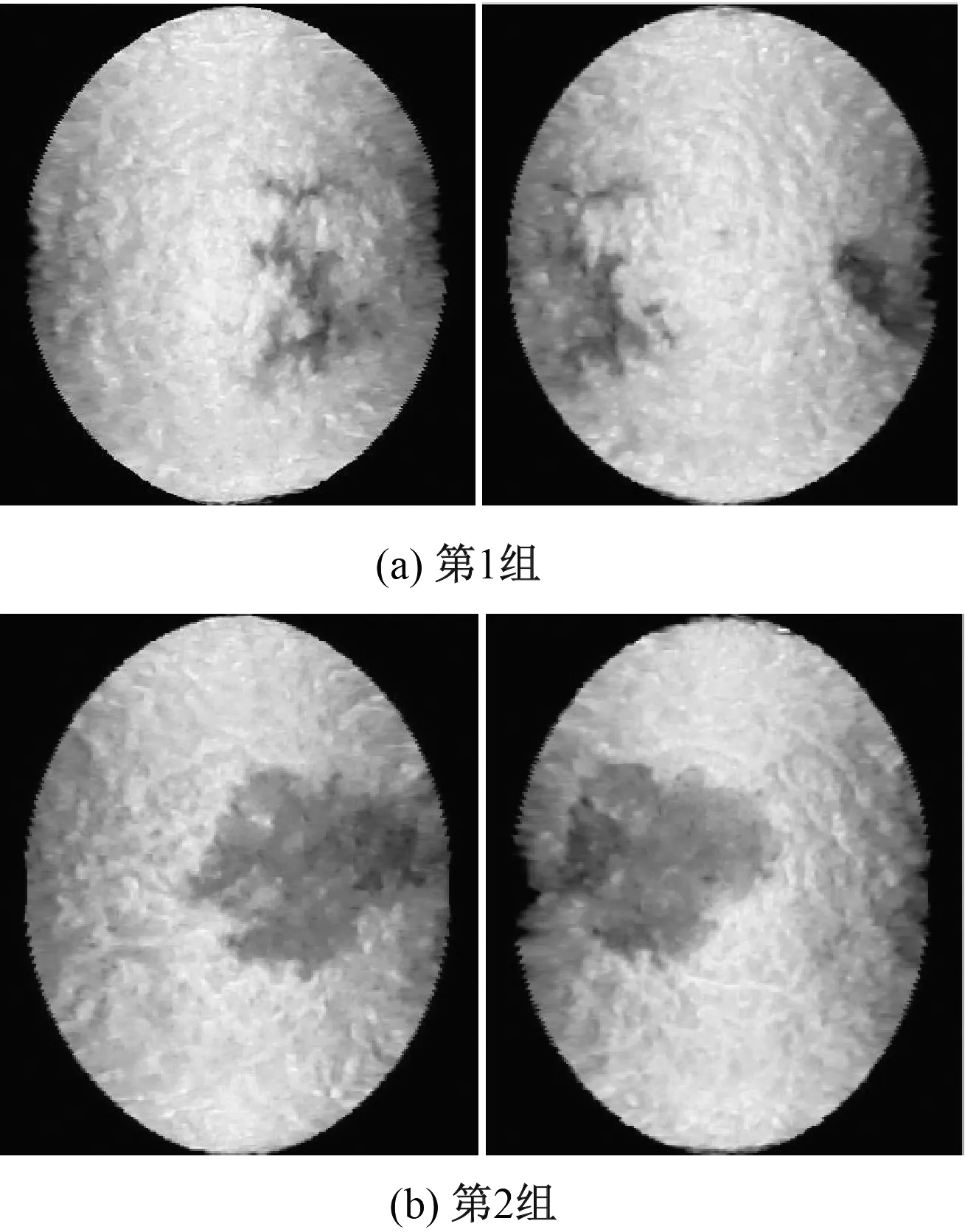
图6 融合前的蚕茧图像

图7 第1组蚕茧图像融合结果

比较可知，通过渐入渐出算法得出的蚕茧融合图像在高纬度区域存在明显的蚕茧边界线，同时蚕茧图像中的黑色背景导致融合图中蚕茧表面区域亮度变暗。采用三角函数权重算法缓解了这一问题，但图像高纬度区域的蚕茧边界线仍然无法消除，无法获得表面平滑过渡且无明显拼接缝的蚕茧融合图像。而本文方法得出的蚕茧融合图像中的蚕茧表面区域自然平滑，接近理想的蚕茧表面图像。

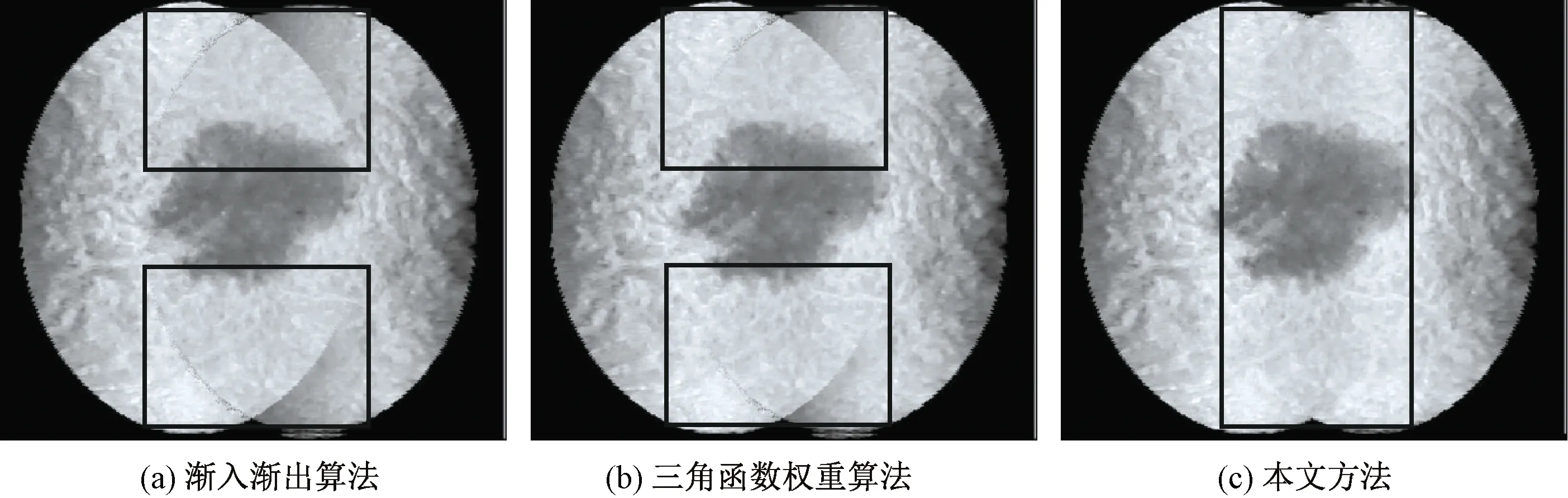
图8 第2组蚕茧图像融合结果

3.2 蚕茧图像融合质量客观指标评估

客观评价指标可分为有参考图像与无参考图像2类[17]。由于蚕茧的特殊性，现实中无法直接获取整张完整的蚕茧表面图像，因此，蚕茧图像融合质量客观评价指标的选取可参照无参考图像的评价指标。无参考图像的评价指标又可分为基于单一图像与基于源图像2类，基于单一图像的评价指标有信息熵、标准差与平均梯度等，用于反映融合图像包含的信息量与灰度值分布情况，基于原图像的评价指标通常采用互信息[18]。

蚕茧融合图像的清晰度与质量对后续疵点检测至关重要，图像越清晰质量越好，疵点面积计算越准确，因此，为在客观数据上反映本文算法的优越性，采用信息熵、平均梯度、空间频率、标准差与互信息作为客观评价指标对蚕茧融合图像进行融合效果评估[15-16]。信息熵反映蚕茧融合图像中所包含的信息量，平均梯度用于衡量图像的清晰程度，空间频率表示图像灰度值的变化率，标准差用于度量图像中信息丰富程度。以上4个指标值越大，则表示蚕茧融合图像越清晰，信息量越大且整体质量越好。互信息用于衡量蚕茧融合图像与原图像之间的相似程度，其值越大表示融合效果越好。评价结果如表1所示。

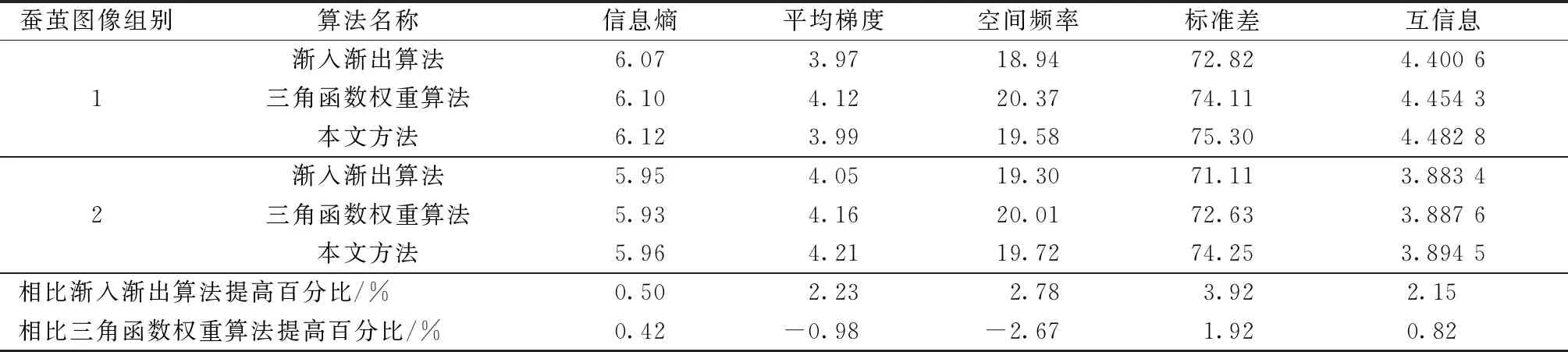
表1 3种方法下蚕茧融合图像客观指标均值对比

根据2组实验结果得出，本文方法得到的信息熵均值比渐入渐出算法提高了0.50%，比三角函数权重算法提高了0.42%。平均梯度均值比渐入渐出算法提高了2.23%，但相比于三角函数权重算法却降低了0.98%。空间频率均值比渐入渐出算法提高了2.78%，但比三角函数权重算法降低了2.67%。标准差均值比渐入渐出算法提高了3.92%，比三角函数权重算法提高了1.92%。综上分析，利用本文方法得到的蚕茧融合图像的平均梯度与空间频率比采用渐入渐出算法大，却略小于三角函数权重算法，但本文方法得到的蚕茧融合图像信息熵与标准差在3种算法中最大。结合以上4种基于单一图像的评价指标结果可以得出，本文方法得到的蚕茧融合图像综合质量最佳且包含的信息量最大，更利于后续蚕茧疵点检测。

本文方法的互信息在3种算法中最大，其均值比渐入渐出算法提高了2.15%，相比于三角函数权重算法提高了0.82%，表明本文方法得到的蚕茧融合图像与蚕茧源图像的相似度更大，融合效果更好。

4 结 论

一般的图像融合算法适用于常规的矩形图像，对蚕茧图像融合的效果不佳。为解决这一问题，本文在蚕茧图像配准的基础上，结合蚕茧表面的形态特征建立蚕茧图像融合的数学模型，并根据椭圆重叠区域的最大宽,设立感兴趣区域代替蚕茧图像的原本重叠区域进行融合处理。与渐入渐出算法和三角函数权重算法相比，本文算法得到的蚕茧融合图像在主观评价上得到明显改善，无明显拼接痕迹。客观评价可反映蚕茧图像的融合效果与蚕茧融合图像质量，根据互信息得出本文算法的融合效果较其他2种算法更好。虽然第2组蚕茧融合图像的平均梯度与空间频率次于三角函数权重算法，但客观指标中信息熵与标准差都高于渐入渐出算法和三角函数权重算法。由于4种指标无优先级，综合分析得出本文方法得到的蚕茧融合图像的图像质量较高，图像包含信息更丰富。