县域国土空间斜坡地质灾害敏感性评价研究

薛永安，王玉洁，朱婧聪，李昊辰，张明媚

（1.太原理工大学矿业工程学院，山西太原 030024；2.山西能源学院地质与测绘工程系，山西晋中 030600；3.中国科学院地理科学与资源研究所中国科学院陆地表层格局与模拟重点实验室，北京 100101）

引言

斜坡地质灾害（本文特指：崩塌、滑坡、不稳定斜坡）敏感性评价的本质是利用数学语言评估在一定地质环境条件下斜坡地质灾害空间概率的敏感性［1］。近年来，国内外学者使用不同的数学模型开展区域地质灾害敏感性评价取得了一定的成果［2～6］，如基于定性评价方法的加权线性组合法［7］，但更多的是基于定量评价方法，采用最邻近的灾害调查数据及该区域过去已发生的各类地质灾害，在连续的尺度上确定地质灾害易发区。目前常用的定量评价模型包括：层次分析法［2］、逻辑回归模型［8］、神经网络法［9］、信息量法［10］、确定性系数法（Certainty Factor，CF）［11］、随机森林（Random Forest，RF）［12］和支持向量机（Support Vector Machine，SVM）［13］等。然而，采用这些定量评价模型通常要求大量的高质量灾害数据，评价结果易受到已知地质灾害数据不准确、精度较低和数量较少的影响，导致评价结果存在较大的不确定性，评价模型适用性因此受限。其中，CF模型［14］和SVM模型［15］模型在地质灾害敏感性评价中应用较为广泛，是统计思想模型和机器学习模型的代表性评价模型，而SVM模型与RF模型又是小样本情况下表现较好的敏感性评价模型。每种评价模型均具有各自的优缺点，单一评价模型往往存在诸多问题，难以客观、定量、准确的进行区域地质灾害敏感性评价［16］，更多的学者开始在同一地区采用不同的模型进行对比研究［17］，选取最优评价模型和评价结果［18］。但是，这些模型均需要大量的样本点进行统计与学习，这对样本数量较少的县域国土空间开展斜坡地质灾害敏感性评价带来制约，选用哪种模型进行评价更可靠应依据县域实际情况结合定性经验进行比选。同时，组合评价模型逐渐成为研究热点［18-20］，如SVM与Newmark的组合模型［21］，CF与AHP、Logistic回归和神经网络多层感知器方法组合的区域滑坡敏感性评价［22］、CF与RF模型的组合［23］、CF与Logistic回归模型组合［24］等，为敏感性评价模型组合研究提供了丰富的方法参考。还有组合与对比同时进行的研究工作［18］，为地质灾害敏感性评价研究提供了坚实的理论与实践参考。

针对县域国土空间斜坡地质灾害敏感性评价，文献［25］采用遥感解译的方式增加了样本数量，提升了基于统计思想的信息量模型的适用性，为开展小范围地质灾害敏感性评价提供了方法参考。但受交通限制，该方法的解译斜坡地质灾害点验证率仅有46.2%，基础数据可靠性不足，评价结果存在较大不确定性。本文采用组合预测模型思想，选择CF模型和SVM模型作为单模型，将CF模型与SVM模型进行组合，开展县域国土空间斜坡地质灾害敏感性评价单模型（CF模型、SVM模型、RF模型）与组合模型（CF-SVM模型）适用性对比研究，以期为县域国土空间规划、国土综合整治、地质灾害防治等小样本情况下地质灾害敏感性评价提供更可靠的评价模型与评价结果。

1 研究区及数据源

1.1 研究区概况

以山西省忻州市五寨县为研究区，研究区位于山西省西北部黄土高原丘陵区，管涔山北麓，地理范围：111°28'～113°00'E和38°44'～39°17'N，共有9乡3镇，行政村250个，总面积为1 391 km2。

研究区地势东南高，为变质岩森林山区；西北低，属于典型的晋西北黄土高原黄土地貌形态；中部地势平坦，为黄土盆地平川区。主要出露地层有：太古界吕梁群地层，上元古界震旦系，古生界寒武系和奥陶系地层。第三系地层和第四系黄土分布于北部和西部丘陵区，在盆地、河谷内为全新近统近代冲洪积物。研究区地质构造处于吕梁山背斜西北翼，偏关台凹南部边缘，横山大断裂中段，区内主要分布有横山断裂、安塘-五寨隐伏断层和青阳岭及小口村断层。地表水均属黄河水系，主要有朱家川河、县川河、岚漪河三大水系。

受自然条件影响，研究区形成了南寒北暖的特殊气候，可分为南部凉爽湿润区、中部温凉半干燥区和北部温和干燥区3种类型。年平均降水量为478.50 mm，多集中在7、8、9月份。年蒸发量1 856.90 mm，约为年降水量的4倍。

研究区内地下矿产资源匮乏，而石灰岩、花岗岩、粘土储量较为丰富，现有各类矿山20余座，主要为建筑石料用灰岩、砂岩、砖瓦用粘土、建筑用辉绿岩和花岗岩矿。

近年来，研究区经济建设快速发展，旅游业开发、基础设施建设、山区修建住房等人类工程活动对地质环境的影响越来越大，地质灾害频发。

1.2 数据源

（1）基础数据

收集到研究区2013年、2017年斜坡地质灾害点93处，基于2017年五寨县地质灾害分布及易发程度分区图（1：50 000）矢量化成果分别提取了研究区地层岩组、地质构造、基础地理信息等数据。其中，地层岩组依次为：砂卵砾石、粉土、粉质粘土多层土体（Q4）、风积粉砂土单层土体（Qeo13）、冲洪积亚粘土、钙质结合层多层土体（Qp11+2）、晚第三系上新统亚粘土钙质结合层多层土体（N2）、薄-中厚层稀裂状较软变质岩风化岩组（A）、厚层块体状硬石英砂岩组（Z）、中厚-厚层稀裂状中等岩溶化硬灰岩组（∈+o）。

（2）DEM数据

以ASTER GDEM V2数据作为数字地形因子提取基础数据，下载地址为：http：//www.gscloud.cn/。

（3）遥感影像数据

以2017年8月11日Landsat8数据为NDVI提取基础数据，下载地址为：http：//www.gscloud.cn/。

空间分析、敏感性评价、结果统计与制图分别基于ArcGIS、SPSS Modeler等软件进行。

2 模型方法

2.1 CF模型

CF值是体现地质灾害发育敏感性的重要因素，1986年，Heckerman［26］对CF模型做出进一步改进，通过将已知的地质灾害隐患点作为基础数据，运用确定性系数法计算研究区CF值。CF取值在［-1，1］，CF值越大，发生灾害的可能性越大，反之亦然。CF=0时无法判断灾害发生可能性。

CF值计算公式如下：

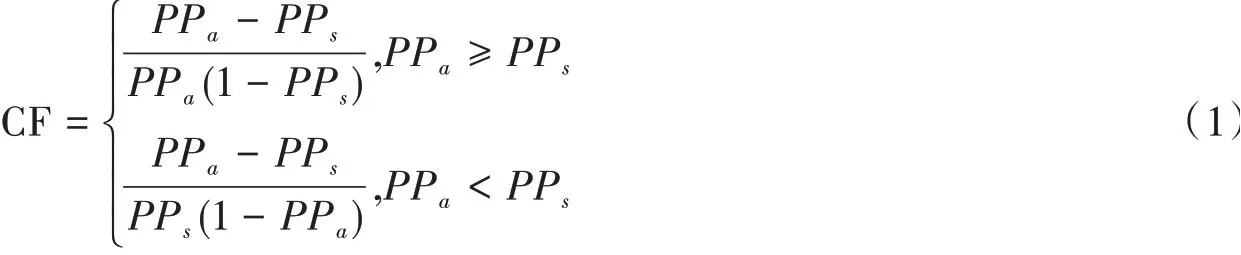
式中：PPa为某一特征a的条件概率；PPs为研究区域的灾害点数量与面积之比；CF为地质灾害发生的确定性系数。

2.2 SVM模型

SVM通过引入核函数有效地解决了非线性分类问题，使得敏感性评价中的非线性分类计算复杂度不再取决于空间维数，而是取决于用于建模的灾害点样本数量，尤其是其中支持向量的灾害点数量。因此，SVM被认为是目前针对小样本统计估计和预测学习的最佳理论，在地质灾害敏感性评价中应用较多［27］。

对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度也越大。最大间隔分类器的目标函数可以定义为根据间隔的定义，有

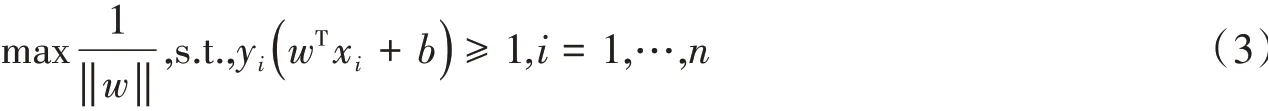
式中：s.t.导出的是约束条件。

2.3 RF模型

随机森林是由决策树构成的集成算法，是利用多棵树对样本进行训练并预测的一种分类器，属于集成学习中bagging框架的方法，具体步骤为：

（1）地质灾害数据集包括N个样本，对数据集进行有放回的抽取，共抽取N次，每次抽取1个滑坡灾害点，共形成N个训练样本集。对N个样本分别建立决策树；

（2）每个地质灾害样本训练集包含M个特征，当决策树的每个节点需要分类时，随机从这M个特征中选取m个特征，满足m＜＜M。然后从这m个特征中采用某种策略来选择1个特征作为该节点的分类特征；

（3）决策树形成过程中每个节点均按步骤（2）分类，直至不能分类为止；

（4）由步骤（1）～（3）建立大量的决策树构成随机森林；

（5）由每棵决策树模型采用投票方式选出最优分类结果。

与SVM模型相比，RF模型引入了样本的随机抽样和特征的随机抽样，大大减少了分类过程中对数据噪声和异常值的敏感性，提高了预测准确率［23］。

2.4 CF-SVM模型

该模型是对CF模型和SVM模型的组合，利用CF方法计算得到各个影响因子的分级CF值，以CF值替代分级统计结果作为SVM模型的分类数据，并将其作为训练样本数据，采用SVM模型进行样本训练，进而对整个研究区栅格数据进行预测，继而得出研究区斜坡地质灾害敏感性评价结果。

2.5 评价因子相关性分析

如果评价因子之间存在高度相关性，CF数模型的精度就会降低甚至失真。本文选用皮尔逊相关分析方法来分析各评价因子之间的相关关系，皮尔逊相关系数Rxy计算公式如式（4）［28］：

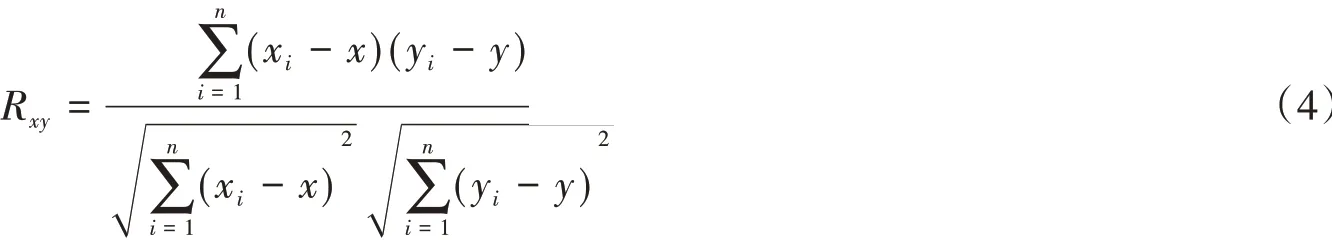
式中：x与y均为评价因子序列，分别代表2个样本，为评价因子序列在相应图层提取值的平均值；Rxy为评价因子两两之间的相关系数，取值范围为［-1，1］，Rxy＞0表示2个因子之间存在正相关性，Rxy＜0表示2个因子之间存在负相关性，|Rxy|越接近于1，表明2个因子之间的相关性越高，|Rxy|越接近于0，表明2个因子之间的相关性越低；xi、yi分别为2个评价因子序列中的第i个因子的值；n为评价因子总数。

3 影响因子分级及敏感性计算

3.1 影响因子

斜坡地质灾害的发生与孕灾环境及诱发因素密切相关，合理的选择评价因子是进行斜坡地质灾害敏感性评价的关键［10］。地形地貌是斜坡地质灾害发育的重要影响因素，其中，高程与人类活动关系密切，影响区域植被类型、植被覆盖度等因素，从而间接性影响斜坡地质灾害的发生。坡度则对坡体剪应力强度有直接的影响，决定了斜坡应力及灾害分布。坡向不同导致光照、风的干湿、降雨、植被覆盖和土壤潮湿程度不同，影响土壤强度和边坡稳定性。地势起伏度表示在特定范围内最高点与最低点之间的高差，与坡体高度密切相关，而坡体高度增大，剪应力也随之变大，发生斜坡地质灾害的概率随之变大。区域地质环境是斜坡地质灾害发育的控制性因素，强烈的剪力作用，使得断层附近的岩石体破碎，活动断层增加了斜坡地质灾害发生的可能性。而地层岩组是斜坡体的构成物质组成，不同的岩性抗风化、水蚀能力不同，导致坡体稳定性随岩性不同而差异较大。人类工程活动众多，各类工程开挖、削坡卸载等引起斜坡体稳定性的减弱，引起崩塌与滑坡灾害。其中，道路工程施工建设中一般需对途经岩土体进行开挖，而开挖会改变地形地貌，常引起边坡失稳，道路工程扰动成为诱发斜坡地质灾害的重要人为动力特征因子。河流水系是区域地表径流大小的体现，在一定程度上反映了该地区的沟谷密度，河流冲刷会降低斜坡坡脚的稳定性，是诱发斜坡地质灾害的重要自然因素，而植被覆盖则具有保持水土的作用，对保障坡体稳定性具有积极作用。

影响因子状态分级是指数据类型为离散型和连续型的单因子指标遵循一定的划分标准分为多个不同范围的二级状态［18］。目前，有研究者采用定量计算选取阈值划分等级［18］，也有研究者根据以往经验与灾害点分布规律进行因子状态分级［10-11，25］。

文中在前期研究的基础［29-31］上结合现有研究［10-11，25］从地形地貌（高程、坡度、坡向、地势起伏度）、地质因素（地质构造、地层岩组）、人为动力（道路工程扰动）和自然因素（河流水系、植被覆盖（NDVI））4个方面选取9个因子作为斜坡地质灾害敏感性评价因子组合（表1），并依据研究经验，综合考虑进行了评价因子状态分级。

表1 研究区斜坡地质灾害敏感性评价因子分级表Table 1 Classification of assessment factors of slope geological hazard sensitivity in the study area

3.2 影响因子CF值计算

根据研究区93处斜坡地质灾害点的分布特征（图1），以公式（1）计算得到各评价因子不同分级的CF值（表2）。

表2 各因子分类等级CF值计算结果表Table 2 Calculation results table of CF of classification level of each evaluation factor

（1）高程（图1（a））。灾害点主要分布于1 300～1 400 m之间，灾害发育数量占总灾害数量的百分比达到44.09%。1 300 m以下次之，灾害发育数量占总灾害数量的百分比为34.41%，但该区间灾害发育密度为0.26处/km2，为区内发育密度最高。2 100 m以上区域无地质灾害发育。

（2）坡度（图1（b））。灾害点主要分布于0～10°和10～20°坡度之间，发育灾害数量分别占总灾害数量的41.94%和38.71%，但0～10°区间面积占总面积的50.13%，因此发育密度相对较小，10～20°和20～30°为灾害发育密度最大坡度区间，均为0.08处/km2。坡度大于40°的区域无地质灾害发育。

（3）坡向（图1（c））。灾害点主要分布于东南向与南向，其次是西南向与西向，发育灾害占总灾害数量的百分比分别为20.43%、20.43%、15.05%、15.05%，东北向相对较少，仅发育2处灾害点。东南向发育密度最高，为0.14处/km2。平坡向无地质灾害发育。

（4）地势起伏度（图1（d））。灾害点主要分布于100～150 m地势起伏区间，发育灾害占总灾害数量的48.39%，且发育密度最大，为0.13处/km2，而25～50 m区间发育地质灾害较少，仅有1处。0～25 m区间无地质灾害发育。

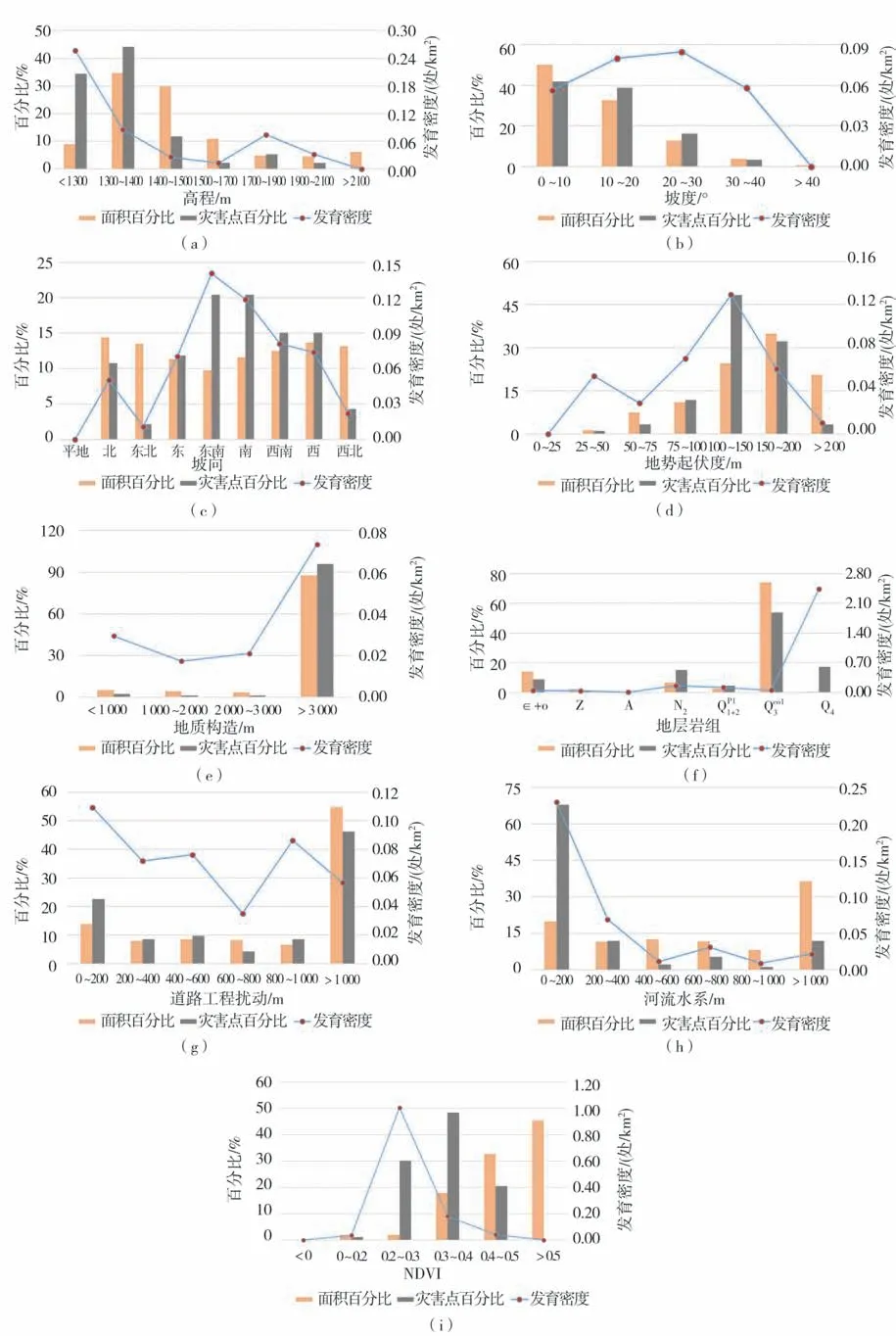
图1 影响因子分级统计结果图Fig.1 The results of statistical classification of influencing factors

（5）地质构造（图1（e））。距离断裂构造3 000 m以内时仅发育4处地质灾害，95.70%的地质灾害点发育在距离断裂构造3 000 m以外，地质构造不是影响研究区地质灾害发育的主要因素。

（6）地层岩组（图1（f））。灾害点主要分布于Qeo13，占总灾害数量的53.76%，其次是Q4，占总灾害数量的17.20%，而A未发育地质灾害。

（7）道路工程扰动（图1（g））。灾害点在距离道路0～200 m时相对分布较多，占灾害总数量的22.58%，发育密度最大，为0.11处/km2。而距离道路大于1 000 m区域发育灾害数量最多，占灾害总数量的46.24%，但发育密度为0.06处/km2。

（8）河流水系（图1（h））。灾害点在距离河流0～200 m范围内发育数量最多，占总灾害数量的67.74%，发育密度也最大，为0.23处/km2，表明研究区地质灾害发育受河流水系的影响较大。

（9）NDVI（图1（i））。灾害点主要发育于NDVI值0.3～0.4、0.2～0.3的区域，分别占总灾害数量的48.39%和30.11%，发育密度分别为0.18处/km2、1.00处/km2，表明研究区地质灾害发育位置植被覆盖度较好。

综合上述分析，研究区地质灾害点受地形地貌影响主要发育于1 400 m高程以下，0°～20°坡度之间，100～150 m地势起伏区间，坡向以东南向、南向为主；受地质因素影响主要分布于Qeo13地层，但受地质构造控制较弱；受人为动力因素影响，距离道路1 000 m以外发育灾害点数量最多，200 m以内相对较多，灾害发育与道路关系密切；受自然因素影响，灾害点主要分布于距离河流200 m以内的区域，受水系影响明显，同时灾害点主要分布于植被覆盖度较高区域。

4 斜坡地质灾害敏感性评价

文中随机选取70%的总样本点和相同数量的非地质灾害单元作为训练样本，其余30%作为测试数据。

4.1 CF模型评价

本文利用ArcGIS软件提取研究区各因子的图层数据，通过皮尔逊相关系数Rxy来衡量各因子的相关度。

经计算，高程与道路工程扰动因子之间具有较强相关性（Rxy=0.816），对比图1，高程因子与道路工程扰动因子相比规律性较弱，因此剔除高程因子，以剩余8个因子构建评价因子集，采用CF模型进行研究区斜坡地质灾害敏感性评价。

4.2 SVM模型评价

在SVM样本训练中利用多种核函数训练，经对比后选取RBF核函数作为预测模型，进而对整个研究区的斜坡地质灾害敏感性进行预测。

4.3 RF模型评价

利用图1的统计结果作为RF模型的分类数据，利用训练样本进行模型训练，调整最优特征数和决策树的个数，对比选出最优预测模型，从而对整个研究区进行预测，得到研究区斜坡地质灾害敏感性评价结果。

4.4 CF-SVM模型评价

采用CF模型计算得到的各评价因子分级CF值作为分类数据输入RBF核函数SVM模型，进行研究区斜坡地质灾害敏感性评价。

4.5 多模型斜坡地质灾害敏感性评价结果

研究区斜坡地质灾害敏感性评价分别采用CF模型、SVM模型、RF模型、CF-SVM模型，将研究区划分为4个敏感性等级，分别为：极高敏感区、高敏感区、中敏感区和低敏感区，采用自然间断点法得到斜坡地质灾害敏感性分区图（图2）和分区统计表（表3），4种模型不同敏感性等级的灾害点比例与面积比例频率比值对比结果见图3。

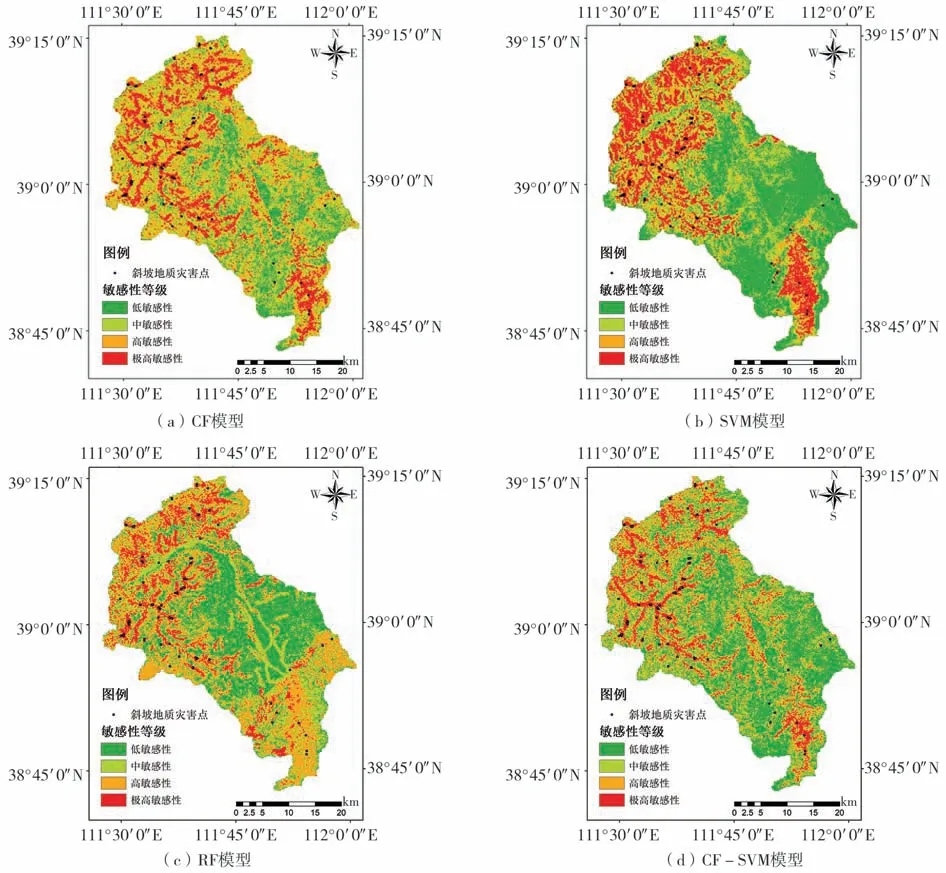
图2 研究区斜坡地质灾害敏感性分区图Fig.2 Slope geological hazard sensitivity zoning in the study area

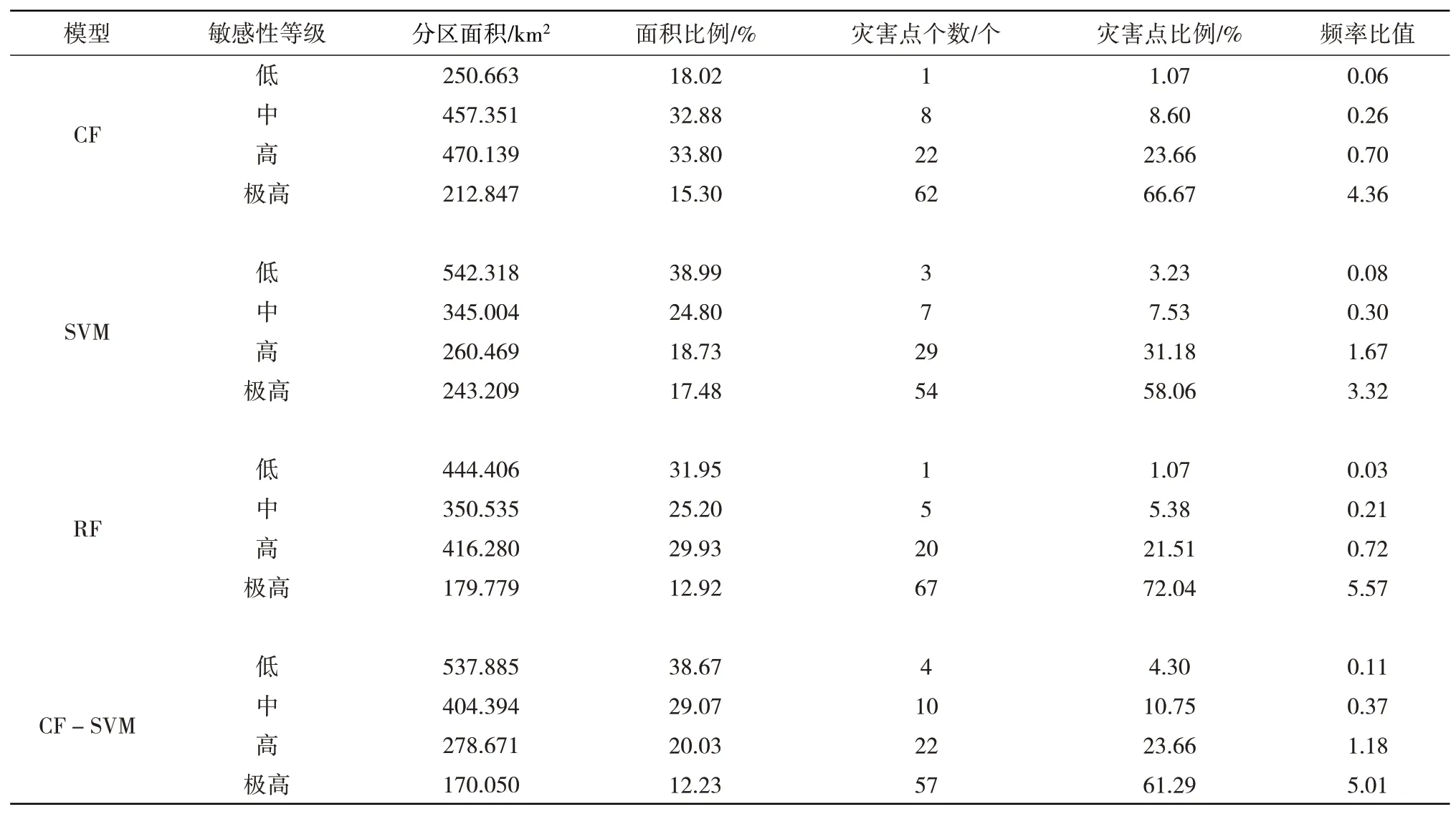
表3 研究区斜坡地质灾害敏感性分区统计表Table 3 Statistical table of slope geological hazard sensitivity zoning in the study area

表3与图3可以看出，4种模型的频率比值均随敏感性等级升高而递增，经对比均符合指数函数，拟合方程分别为：（1）y=0.014 7e1.3848x，R²=0.987 7；（2）y=0.024e1.2894x，R²=0.976 3；（3）y=0.005 8e1.6904x，R²=0.991 7；（4）y=0.029 9e1.2616x，R²=0.997 6。其中，决定系数R²的值均接近于1，表明4种模型的频率比值与敏感性等级之间呈良好的正相关，而CF-SVM模型所划分的敏感性等级与频率比值相关性最好（R²=0.997 6）。

图3 灾害点比例与面积比例频率比值对比图Fig.3 Comparison of the frequency ratio by the proportion of disaster points and the proportion of area

4.6 精度检验

ROC曲线下面积AUC值可以用来确定预测模型精度等级［27］：（1）极好：0.9～1；（2）非常好：0.8～0.9；（3）好：0.7～0.8；（4）一般：0.6～0.7；（5）差：0～0.6。

本文采用ROC曲线评价精度，利用占总样本30%的未参与模型训练的28个样本点进行检验，保证所建模型的客观与稳定。ROC曲线及统计结果分别见表4和图4。

图4 ROC曲线图Fig.4 ROC curve

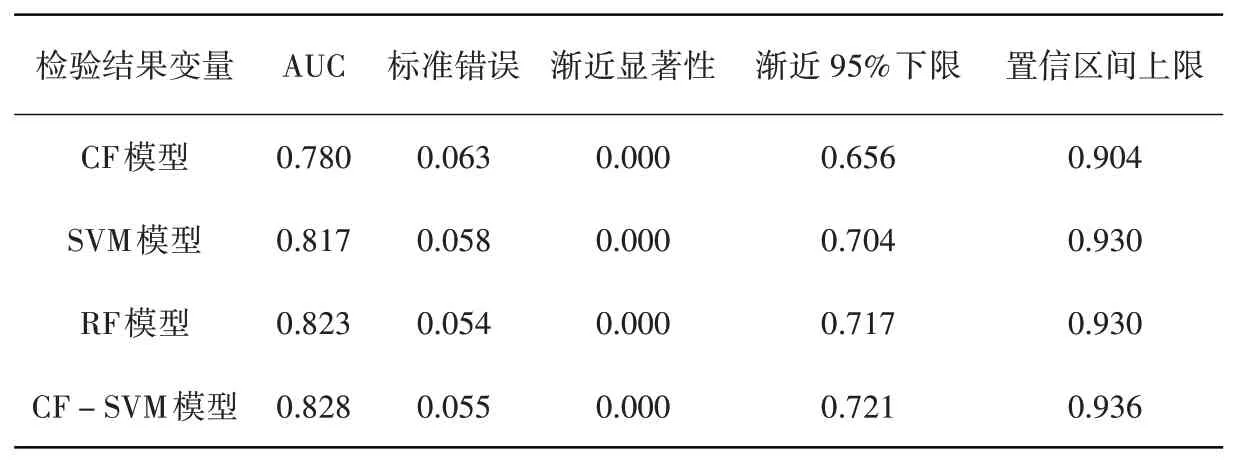
表4 ROC曲线统计表Table 4 Statistical table of ROC curve

4.7 讨论

（1）CF模型首先进行了评价因子相关性分析，剔除有较强相关性的高程因子，保留线性无关的8个因子开展评价。图1统计结果显示，灾害点主要分布于1 300～1 400 m高程区间，占总灾害数量的44.09%。结合经验分析，高程是斜坡地质灾害发育的重要地形影响因子，因相关性而剔除高程参与计算对评价结果具有一定的影响。而SVM模型、RF模型和CF-SVM模型均采用全部评价因子开展评价，消除了重要影响因子可能被剔除所引起的评价风险。

（2）表3显示，CF模型、SVM模型、RF模型和CF-SVM模型的敏感性分区结果中极高敏感区的频率比值分别为4.36、3.32、5.57和5.01，而低敏感区的频率比值分别为0.06、0.08、0.03和0.11，RF模型在极高敏感区的频率比表现最佳，其次是CF-SVM模型，均以更小的分区面积分布了更多的斜坡地质灾害点。由表4可以看出，CF模型、SVM模型、RF模型和CF-SVM模型的AUC值分别为0.780、0.817、0.823和0.828，渐进显著性均小于0.05，表明4种模型均较好，其中，CF模型的精度为好，SVM模型、RF模型和CF-SVM模型的精度为非常好，且CF-SVM模型精度高于其他3种模型。

（3）由图2可以看出，CF模型与RF模型受水系因子影响较大，所划分极高敏感区主要沿水系分布，呈明显的树杈状；SVM模型体现出多因子的综合作用，所划分极高敏感区主要分布于西部黄土丘陵区与东南部土石山区，西部丘陵区沟谷纵横、水土流失严重，是黄土崩塌、滑坡发育的潜在隐患区；CF-SVM模型所划分极高敏感区保持了CF模型的特点，沿水系走向分布，而低敏感区则保持了SVM模型的特点，主要分布于中部平原区。

（4）图3表明，4种模型的频率比值趋势一致，均呈现指数特征。CF模型所划分极高、高敏感区总面积为682.986 km2，占研究区总面积的49.10%，灾害点分布占总灾害点的90.33%；SVM模型所划分极高、高敏感区总面积为503.678 km2，占研究区总面积的36.21%，灾害点分布占总灾害点的89.24%；RF模型所划分极高、高敏感区总面积为596.059 km2，占研究区总面积的42.85%，灾害点分布占总灾害点的93.55%；CF-SVM模型所划分极高、高敏感区总面积为448.721 km2，占研究区总面积的32.26%，灾害点分布占总灾害点的84.95%。

5 结论

（1）CF模型、SVM模型、RF模型和CF-SVM模型精度均较高，AUC值分别为0.780、0.817、0.823和0.828，预测精度由高到低依次为：CF-SVM模型＞RF模型＞SVM模型＞CF模型，CF-SVM模型较CF模型、SVM模型和RF模型预测精度分别提升了6.15%、1.35%和0.61%，是4种模型中更适合县域国土空间斜坡地质灾害敏感性评价的模型。

（2）综合频率比值、AUC值和敏感性分区图，CF-SVM模型融合了CF模型与SVM模型的优点，既保证了更多的斜坡地质灾害点分布于极高、高敏感区，模型精度非常好，又保证了极高、高敏感区面积相对较小，符合斜坡地质灾害分布实际情况，是CF模型与SVM模型综合赋能预测结果的体现，兼顾了评价精度与结果合理性，模型适用性更好。

（3）CF-SVM模型所划分地质灾害低敏感区、中敏感区、高敏感区和极高敏感区的面积分别为：537.885 km2、404.394 km2、278.671 km2和170.050 km2，分别占研究区总面积的38.67%、29.07%、20.03%和12.23%，所分布灾害点分别占总灾害点的4.30%、10.75%、23.66%和61.29%，灾害点比例随敏感性等级升高而递增，与敏感性等级之间呈现良好的正相关。

（4）本文系统性开展了县域国土空间小样本斜坡地质灾害确定性系数模型（CF）、支持向量机模型（SVM）、随机森林模型（RF）和组合模型（CF-SVM）敏感性评价精度与结果对比，为类似研究与防灾减灾工作提供了技术参考。

本文所选评价因子中未考虑降雨、地震等影响，今后应继续完善评价因子集，同时，应进一步考虑更多模型参与评价与组合，对比遴选最优评价模型。