亚塑性模型对土-结构相互作用问题的预测能力分析
2022-09-22刁红国王新泉崔允亮张天赐
刁红国,王新泉,魏 纲,崔允亮,张天赐
(1.浙大城市学院工程学院,浙江杭州 310015;2.浙江省城市盾构隧道安全建造与智能养护重点实验室,浙江杭州 310015;3.城市基础设施智能化浙江省工程研究中心,浙江杭州 310015)
引言
土是一种复杂的多相介质材料,能够真实反映其材料特性的本构模型对于数值模拟计算结果的可靠度至关重要。评价一个本构模型是否可靠,关键在于其是否能够较好地描述土体的应力应变关系。目前常用的土体本构模型包括线弹性和多孔介质弹性模型、Mohr-Coulomb模型、修正Drucker-Prager帽盖模型和临界状态塑性模型等。随着城市建设的快速发展,邻近基坑、隧道与桩基之间的相互影响问题备受关注,属于典型的土-结构相互作用问题[1-3]。采用数值模拟研究时,本构模型也由简单的理想弹塑性模型[4-7]逐渐拓展至邓肯-张非线性模型[8]、修正剑桥模型[9]和土体硬化模型[10]。
Atkinson等[11]将土体应变定义为非常小应变(不大于0.001%)、小应变(在0.001%与1%之间)和大应变(大于1%)3个范围。Mair[12]和汪中卫等[13]统计了不同岩土工程条件下的典型土体应变范围,发现基坑或隧道开挖引起周围土体的剪应变分布在0.01%~1%之间,属于小应变范围。而且,土体刚度具有应力路径依赖性和应变依赖性,即土体刚度只有在应变非常小时才近似恒值,随后会随着应变增大而弱化[14-15]。因此,本构模型能否描述小应变条件下的土体刚度特性对预测土-结构相互作用问题至关重要。然而,上述数值分析所采用的本构模型并不能反映这一点。亚塑性(Hypoplastic)模型基于亚塑性理论和临界状态土力学理论,不区分弹塑性,直接建立应力率和应变率之间的关系,能够考虑时间的影响,准确描述土体刚度的应力路径依赖性和应变依赖性(即使在小应变情况下)。目前,已有学者[16-17]将其用于模拟开挖卸荷对邻近既有桩基的影响,但亚塑性模型对土-结构相互作用问题的预测能力还鲜有研究。
1 亚塑性模型理论
Kolymbas[18]于1991年首次提出了亚塑性理论的基本方程,即用单一非线性速率类型张量函数来模拟非弹性材料的性能。其应力率分为两部分:第一部分与应变率呈线性关系,第二部分与应变率呈非线性关系,并表示为应变率的范数形式。此后,Lanier等[19]推导了亚塑性本构方程的一般表达式:

为了使亚塑性模型能够考虑应力水平和密度的影响,描述不同应力水平和密度时散粒体的力学状态,Gudehus[20]改进了一般表达式:
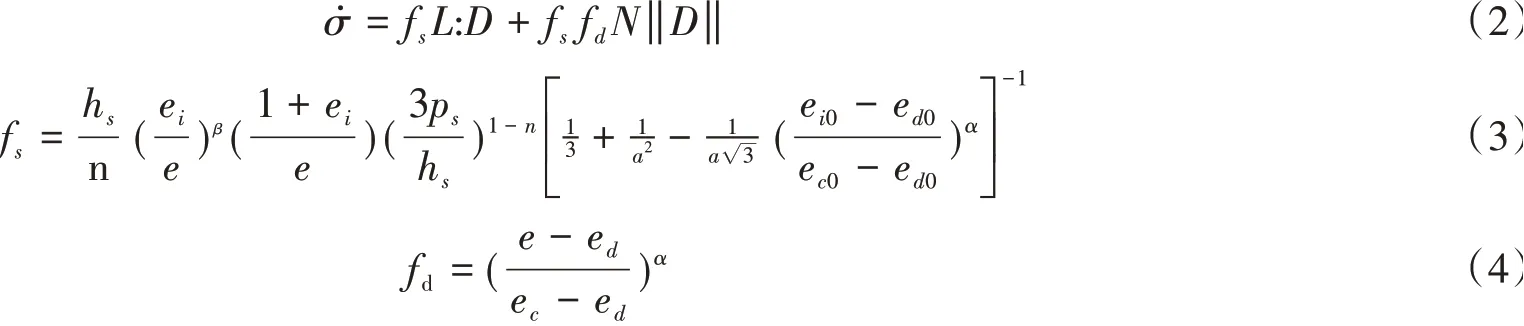
式中:fs是与密实度相关的刚度因子;fd是仅与孔隙比相关的向密性因子;ei、ed和ec分别表示最大孔隙比、最小孔隙比和临界孔隙比;ps是平均应力;ei0、ed0和ec0则分别表示平均应力为0时的最大孔隙比、最小孔隙比和临界孔隙比;hs是应力的量纲,表示颗粒硬度;指数n为常数;α和β分别为介于0至1和略大于1的无量纲参数;参数a仅与土的临界摩擦角有关。
Bauer[21]结合试验和数值模拟对上述模型参数进行标定,提出了可以考虑孔隙比的Gudehus-Bauer亚塑性模型。尽管该模型可以有效模拟在较大密度和压力变化范围时的颗粒体力学性质,但无法恰当地描述土体的临界状态面形状。进一步,von Wolffersdorff[22]引入Matsuoka-Naka准则来描述临界状态下的极限状态,该临界状态面的形状仅与临界状态摩擦角有关,可以模拟颗粒体的破坏过程,总共需要确定以下8个参数:
(1)φc为临界状态摩擦角;
(2)hs,n为控制孔隙比曲线形状(正常压缩曲线和临界状态线)的颗粒硬度和无量纲参数;
(3)ei0、ed0和ec0为平均应力为0时的最大孔隙比、最小孔隙比和临界孔隙比;
(4)α为控制峰值摩擦角随相对密度变化的无量纲参数;
(5)β为控制土体刚度随相对密度变化的无量纲参数。
Kuwano等[15]和Gasparre[23]通过三轴压缩试验得到的土体刚度和应变关系曲线,发现土体具有应变依赖性。Atkinson等[14]通过采用重塑伦敦黏土土样开展排水条件下的单元试验,发现土体还具有应力路径依赖性的。为了实现亚塑性模型能够描述土体在小应变条件下的应变依赖和应力路径依赖性,Niemunis等[24]通过提出“颗粒间应变概念”又进一步对von Wolffersdorff的亚塑性模型作出了改进,认为应变包括颗粒骨架的重组变形和颗粒界面间的变形。最终,为了能够描述土体的小应变特性,除了上述8个基础本构参数,还需要以下5个参数:
(1)mR为控制初始加载及应变路径180°反转时的初始刚度的参数;
(2)mT为控制应变路径90°反转时的初始刚度的参数;
(3)R为应变空间中弹性范围的大小;
(4)βr和χ为控制刚度随应变变化速率的参数。
2 模型建立
为了评价亚塑性模型对土-结构相互作用问题的预测能力,本文以Leung等[25-26]的经典离心模型试验为基础,建立相应的数值模型,分别采用亚塑性和理想弹塑性Mohr-Coulomb两种土体本构模型。此外,考虑到离心模型试验的基本原理是通过提高重力加速度将缩尺模型的土体表现为与原型尺寸土体相同的应力状态,为了探究数值模拟时究竟采用哪种土体尺寸可以更好地预测离心模型的试验结果,本文进一步采用2种不同的建模方法展开讨论:(1)“超重力离心状态+模型尺寸”,即数值模型采用试验模型尺寸,同时增大重力加速度至50 g,完全模拟离心试验条件;(2)“常重力状态+原型尺寸”,即数值模型采用原型尺寸,重力加速度始终为1 g。详细数值分析方案如表1所示。

表1 数值分析方案Table 1 Plan for numerical analyses
2.1 结构参数
图1为Leung等[25-26]开展的平面应变条件下,无支撑基坑开挖对既有单桩或群桩影响的离心模型试验。除桩基形式外,两组试验的条件完全相同,其中图1(a)选择原文献[25]中PC2组的单桩,图1(b)选取原文献[26]中G11组的2×2群桩。模型箱尺寸长×宽×高为540 mm×200 mm×470 mm,离心加速度为50 g。基坑开挖深度为90 mm(原型4.5 m),宽度为400 mm(原型20 m),基坑-桩的水平距离为60 mm(原型3 m)。
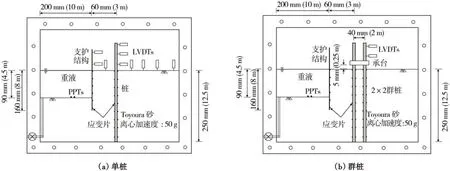
图1 离心模型试验示意图Fig.1 Schematic diagram of centrifugal model test
两组离心模型试验中桩和基坑支护结构的相关参数如表2所示[25-26]。经原型参数换算,模型桩可等效为直径630 mm的混凝土灌注桩,基坑支护结构可等效为KSP-ⅡA型拉森钢板桩。

表2 离心模型试验参数[25-26]Table 2 Parameters of centrifuge model[25-26]
2.2 模型边界条件设置
本文采用ABAQUS有限元软件进行模拟,三维数值模型采用结构化网格划分方法,基坑支护结构和土体模型选用八节点六面体实体单元(C3D8),桩基模型选用四节点壳体单元(S4)。桩-土界面设置零厚度的摩擦接触,采用库伦摩擦法则,包含接触面摩擦系数μ和桩-土相对滑移极限值γcrit两个参数。其中,根据Ng等[27]通过直剪试验对桩-土界面(环氧树脂-Toyoura砂)摩擦特性的研究,桩-土接触面摩擦角δ为29°;摩擦系数μ为0.55;相对滑移极限值γcrit采用Peng[28]通过接触面直剪试验测得的结果5 mm。群桩承台与桩基交界面采用Tie接触。数值模型的底面边界采用固定约束,竖向边界则采用垂直于侧边的滑动约束,不会发生水平位移。最终建立如图2所示的三维数值模型[25-26]。
2.3 本构模型参数
离心模型试验未考虑孔隙水的影响,材料采用均质Toyoura干砂。该标准砂的材料特性已经得到国内外学者的系统研究,相应的Mohr-Coulomb本构模型参数和亚塑性本构模型参数分别采用表3和表4所示的数据。

表3 Toyoura砂的Mohr-Coulomb模型参数Table 3 Parameters of Toyoura sand used in Mohr-Coulomb model
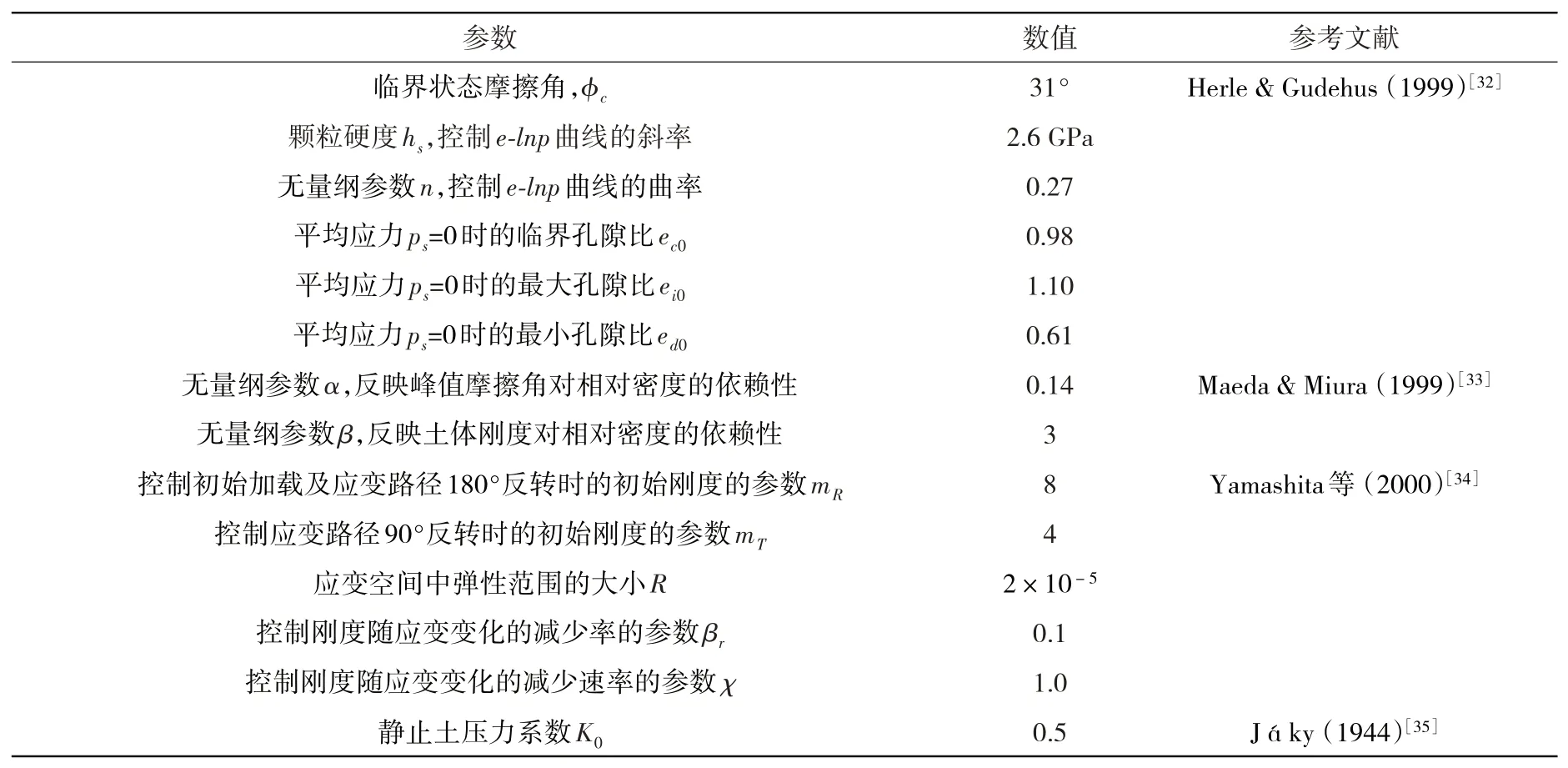
表4 Toyoura砂的亚塑性模型参数Table 4 Parameters of Toyoura sand used in hypoplastic model
2.4 数值模拟过程
以单桩和“超重力离心状态+模型尺寸”的建模方法为例,如图3所示,具体模拟过程如下:
(1)首先建立如图3(a)所示的三维数值模型,设置初始边界条件,完成初始地应力平衡:建立1 g条件下的初始应力场,静止土压力系数K0取0.5。考虑离心模型试验中的基坑开挖采用“排重液法”,对于基坑中的ZnCl2重液,采用在基坑侧壁和坑底施加与离心模型相等的荷载来模拟;

图3 数值模拟过程示意图Fig.3 Idealised numerical modelling procedure
(2)逐步增加重力加速度至50 g,同时增大作用在基坑侧壁和坑底的荷载,模拟离心模型试验正常运行时的应力水平;
(3)激活“wished-in-place”桩(离心试验中的模型桩是在1 g条件的撒砂过程中完成安装,无需考虑打桩过程对桩基受力变形和周围土体扰动的影响,因此称之为“wished-in-place”桩);
(4)分级逐步减小作用在基坑侧壁和坑底的荷载,分层完成基坑的模拟开挖。
3 预测结果
3.1 本构模型对预测结果的影响
图4为Leung等[25]中单桩桩身水平位移和弯矩试验值与模拟值的对比结果。可见,在桩头无约束的条件下,采用悬臂支护结构的基坑开挖引起邻近桩基的最大水平位移发生桩头处,且沿桩身深度逐渐衰减;最大桩身弯矩发生在支护结构底部深度附近,因桩头和桩端处无约束,其弯矩均为零。采用Mohr-Coulomb模型得到的桩身水平位移在桩身中下半段要明显比试验值偏大,而桩头最大水平位移值低估了约16%;采用亚塑性模型得到的桩身水平位移分布特性与离心模型试验相似,最大水平位移值高估了8%左右。两种本构模型得到的桩身弯矩分布均与离心模型试验相似,但前者计算得到的最大弯矩值比试验值偏高13%,后者仅为2%。

图4 离心模型试验与数值模拟结果的对比分析Fig.4 Comparisons between measured results and numerical results
图5为Leung等[26]中2×2群桩桩身水平位移和弯矩试验值与模拟值的对比结果。可见,由于群桩承台的存在,导致距离基坑较近的前桩和距离基坑较远的后桩表现出不同的附加响应。如图5(a)所示,对于前桩,基坑开挖卸荷引起周围土体发生变形,导致桩身水平位移整体朝基坑方向;1.5 m以上桩身(约1/3基坑开挖深度)的水平位移较大,但向上至地表呈现衰减的趋势,这是因为承台具有一定的约束作用和后桩的拖曳作用。对于后桩,在周围土体变形和承台约束拖曳的双重作用下,其桩身水平位移整体朝基坑方向,最大位移发生在地表桩头位置,且地表处前桩和后桩的水平位移一致。进一步,对比试验值与模拟值可知,无论采用Mohr-Coulomb模型还是亚塑性模型,数值模拟得到的前后桩桩身水平位移分布规律均与离心模型试验相似,但前者计算得到的最大水平位移值高估了22%左右,后者高估了7.5%左右。如图5(b)所示,对于前桩,桩身最大正负弯矩分别发生在基坑支护结构深度附近和1/3基坑开挖深度附近。对于后桩,桩身最大正负弯矩分别发生在基坑开挖深度下方附近和地表位置,且桩身大部分产生正弯矩(即靠近基坑一侧的桩身表面出现压应变)。由于承台的存在,前桩和后桩的桩头位置均产生了较大的负弯矩,这与单桩自由无约束时不同。对比可见,采用Mohr-Coulomb模型和亚塑性模型也能反映出群桩桩身弯矩的分布特性,但后者计算结果明显比前者更接近试验值。

图5 离心模型试验与数值模拟结果的对比分析Fig.5 Comparisons between measured results and numerical results
可见,由于Mohr-Coulomb模型高估了桩身大部分水平位移和弯矩,在工程实践应用中可能会获得过于保守的预测结果。两种本构模型预测结果的差别主要是由于二者的理论框架不同,Mohr-Coulomb模型预测的土体刚度为常数,且其初始剪切模量G0较小,而亚塑性模型预测的土体刚度会随着应变(包括小应变)的增大而衰减。基坑开挖卸荷会引起周围土体的应力状态和应力路径发生显著变化,而土体又具有应力路径依赖性和应变依赖性,因此,亚塑性模型更能准确描述土体刚度在开挖过程中的变化趋势。综上所述,亚塑性模型能够更好地反映土-结构相互作用问题中的结构变形和受力特性。
3.2 建模方法对预测结果的影响
图6和图7为采用上述“超重力离心状态+模型尺寸”和“常重力状态+原型尺寸”两种建模方法得到的模拟结果,包括单桩和群桩的附加水平位移和桩身弯矩[25-26]。对比可见,在两组试验中,采用模型尺寸和原型尺寸得到的模拟结果基本相似。由图6可知,对于基坑开挖对单桩的影响问题研究,采用“常重力状态+原型尺寸”建模方法得到的最大桩身水平位移和桩身弯矩仅比“超重力离心状态+模型尺寸”建模方法分别偏小6%和4%左右;由图7可知,对于基坑开挖对群桩的影响问题研究,采用“常重力状态+原型尺寸”建模方法得到的最大桩身水平位移和桩身弯矩比“超重力离心状态+模型尺寸”建模方法分别偏小7%和9%左右。这表明只要实现土体的应力水平与原型场地一致,采用哪种数值模型尺寸对模拟结果的影响并不大。然而,为了真实模拟离心模型试验的全过程,建议采用“超重力离心状态+模型尺寸”的建模方法进行计算分析。
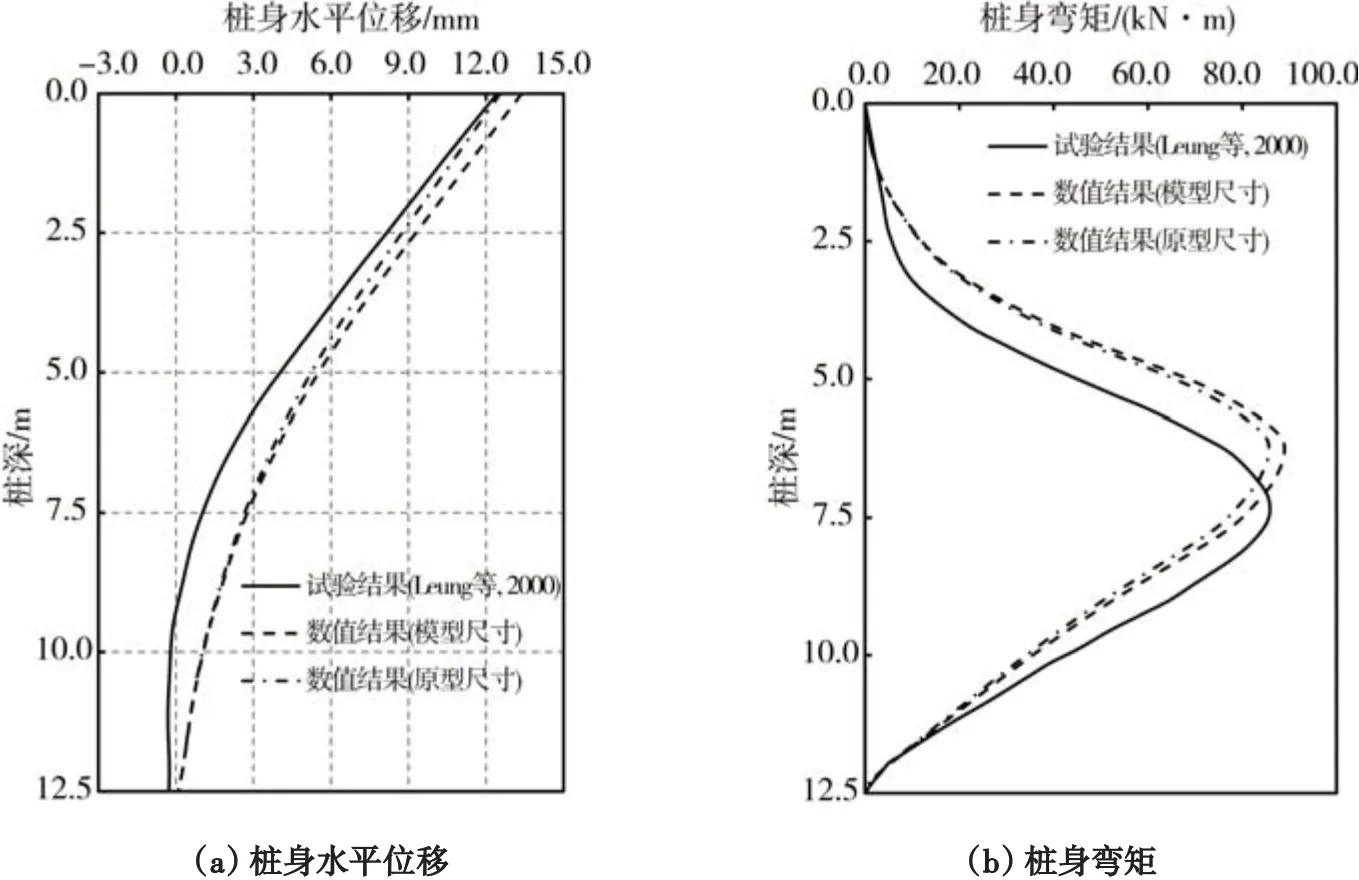
图6 基于模型尺寸和原型尺寸的数值模拟结果Fig.6 Comparisons of numerical results based on model scale and prototype scale

图7 基于模型尺寸和原型尺寸的数值模拟结果Fig.7 Comparisons of numerical results based on model scale and prototype scale
4 结论
本文以Leung等人的两组经典离心模型试验为例,基于不同的土体本构模型与建模方法进行计算分析,主要得到以下结论:
(1)在模拟土-结构相互作用问题时,采用Mohr-Coulomb模型和亚塑性模型均能得到与离心试验结果相似的受力与变形规律,但由于后者能够描述土体的应变依赖和应力路径依赖性(即使在小应变情况下),计算值与试验值的吻合度更佳,预测能力更好。
(2)对于基坑开挖对既有单桩的影响问题,采用Mohr-Coulomb模型的水平位移计算值明显大于试验值,最大弯矩比试验值偏高13%;而采用亚塑性模型的最大水平位移仅高估8%左右,最大弯矩仅偏高2%。
(3)对于基坑开挖对既有群桩的影响问题,需要考虑承台的约束作用和拖曳效应;Mohr-Coulomb模型计算得到的最大水平位移比试验偏高22%左右,亚塑性模型仅偏高7.5%左右,且后者可以更好地预测桩身的附加弯矩特性。
(4)在保证土体应力水平与原型场地一致的前提下,采用“超重力离心状态+模型尺寸”和“常重力状态+原型尺寸”两种建模方法得到的模拟结果相差不大,但为了真实模拟离心模型试验的全过程,建议采用第一种方法。
