倒梯形布筋方式的加筋土挡墙承载破坏性能分析

2022-09-22王家全祁航翔林志南

自然灾害学报 2022年4期

王家全，祁航翔，梁宁，林志南

（1.广西科技大学土木建筑工程学院，广西柳州 545006；2.广西壮族自治区岩土灾变与生态治理工程研究中心，广西柳州 545006）

引言

公路边坡是将地质体的一部分改造成人为工程设施的重要构造物，其安全性和稳定性直接影响公路正常运营［1］。针对公路边坡滑塌和岩溶土洞塌陷处理，众多学者表明土中加入筋材，可以大幅提高土体的强度［2-3］，而加筋土挡墙是防治公路边坡滑塌的最常用支挡构筑物，可有效的防治公路边坡滑塌现象的发生，同时也在世界各国工业与民用建筑、水利水电工程、铁道、桥梁、港口、河流堤岸及航道等工程中得以广泛应用。国内外众多学者从试验、理论、数值模拟等方面对加筋土挡墙的工作性能做了大量的研究工作，促进了加筋土挡墙在工程建设中的推广应用。

在试验方面，肖成志等［4］分析了条形基础距挡墙面板的距离对基础极限承载力、挡墙变形特点、筋材应变以及破坏模式的影响，认为加筋挡墙的破坏主要以3种模式为主；李丽华等［5］探讨了加筋层数、加筋长度以及不同加筋材料（单向土工格栅和废旧轮胎）等因素对加筋土挡墙力学性能的影响，得到了废旧轮胎加筋效果优于单向土工格栅；王家全等［6］通过MTS加载系统开展室内加筋桥台挡墙破坏试验，分析不同格栅长度的加筋土挡墙变形和受力规律，发现动载下不同土工格栅长度及类型的加筋桥台挡墙破坏模式存在差异；Ehrlich［7］研究了2种不同压实状态下对土工格栅加筋土挡墙性能的影响；Li等［8］通过室内模型试验，研究了粉煤灰-砂土混合填料加筋挡土墙的变形特性和极限承载力。结果表明，加筋能有效提高挡土墙的承载力，降低竖向沉降和挠度。

在理论方面，徐鹏等［9］基于双楔块法，通过极限分析理论推导了加筋土挡墙屈服加速度系数表达式；王宗建等［10］以弹性索理论为基础，提出了一套加筋土挡墙在差异性沉降下筋材应力分布及其变形曲线的计算方法；莫介瑧等［11］以试验结果和规范采用的0.3 H法为基础，运用极限平衡理论和参数分析法，提出了台阶式加筋土挡墙潜在破裂面的计算模式；Ahmadabadi［12］基于水平切片法和极限平衡法的分析方法，考虑了加筋土和无筋土的粘聚力对挡土墙主动土压力的影响，提出了一种计算挡墙主动土压力的新方法；Rao［13］提出了一种新的计算刚性挡土墙背面主动土压力的简化方法，并考虑了粘性回填土的土拱效应，利用极限平衡法得到了主动土压力系数的解析表达式。

在数值模拟方面，Rowe等［14］采用有限元程序得出当筋材长度较短（即L/H＜0.7）时，回填土的内摩擦角对挡墙面板水平变形影响显著；Chandra等［15］通过现场试验和数值模拟分析了挡墙的水平位移、筋材的应力应变等规律；周淮等［16］采用颗粒流程序PFC2D对水平-竖向（H-V）加筋土挡墙的作用机理和破裂面形式进行了数值分析，通过土颗粒的位移场和应力场揭示了H-V加筋土挡墙发生渐渐破坏的成因；周健等［17］通过离心模型试验和FLAC2D数值模拟，探讨了包裹式加筋土挡墙在改变筋材长度、筋材间距、刚度等因素对挡墙的变形进行研究，发现筋材的布置间距对挡墙的变形最为显著；徐超等［18］采用FLAC2D程序分析了有限填土加筋土挡墙的稳定性及破坏模型，得出加筋土挡墙的稳定系数随着加筋间距的减小和加筋长度的增加而增加；郑俊杰等［19］通过FLAC3D分析了在加筋土挡墙的加筋区后设置EPS板对抗滑桩-加筋土挡墙支挡结构工作性能的影响，得出设置EPS板能明显降低组合支挡结构在施工期和竖向荷载作用下的墙背土压力、墙面水平位移、桩身水平位移和桩身弯矩，但竖向荷载作用下的顶面差异沉降显著增大。

综上所述，以上学者主要以等长布筋方式研究加筋土挡墙的力学性能，对于倒梯形布筋方式的加筋土挡墙研究鲜有报道。鉴于此，本文以室内模型试验为基础，通过FLAC3D数值模拟研究倒梯形布筋方式加筋土挡墙，分析条形基础偏移距离D对基础的极限承载力、挡墙面板的水平位移、筋材应力以及挡墙潜在破裂面分布规律的影响，为顶部承受桥台基础作用的加筋土挡墙的建设和推广提供参考依据。

1 室内模型试验和数值模型建立

1.1 加筋土挡墙室内模型简介

室内模型试验中模型箱尺寸为1 500 mm×1 000 mm×1 300 mm（长×宽×高），加载板采用950 mm×150 mm×30 mm（长×宽×厚）的钢板模拟加筋土挡墙顶部条形基础，基础偏移距离D=0.45 H（H为墙高），筋材分4层布置，层间距为23 cm，筋材长度从上到下依次为1.0 H、0.8 H、0.6 H、0.4 H，如图1所示。

试验所用填料为柳州本地的河砂，砂土的具体物理参数如表1所示，筋材采用双向拉伸HDPE土工格栅，产品规格为TGSG3030，材料的具体参数如表2所示。依据《公路工程技术标准》（JTG B01-2014）［20］采用分级加载的方式进行室内模型试验。

表1 砂土的物理参数Table 1 Physical parameters of sand

表2 土工格栅材料参数Table 2 Geogrid material parameters

1.2 加筋土挡墙数值模型建立

采用FLAC3D三维建模软件建立与室内模型尺寸相同的数值模型，如图2所示。数值模型的边界条件设置为左侧面板以及顶部自由，其余3个侧面限制法向位移，底面限制法向和切向位移。砂土采用Mohr-Coulomb模型，土工格栅采用FLAC3D自带的Geogrid单元进行模拟，挡墙面板采用弹性模型，根据材料实际的属性，来确定数值模型中砂土、面板以及土工格栅的参数，如表3、表4所示。

表4 土工格栅单元参数Table 4 Geogrid unit parameters

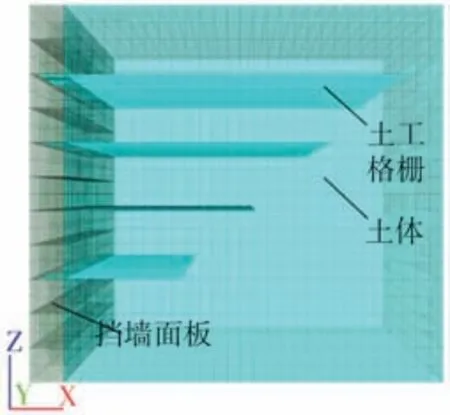
图2 加筋土挡墙数值模型Fig.2 Numerical model of reinforced soil retaining wall

表3 填料及面板参数Table 3 Soil and panel parameters

1.3 加筋土挡墙数值模型验证

为了验证数值模型的可靠性，基于室内模型试验结果，对倒梯形加筋土挡墙数值模型进行验证。图3为数值模拟基础偏移距离D=0.45 H与室内模型试验实测条形基础的基底压力-沉降曲线，数值模拟结果和室内模型试验结果具有很好的吻合性，说明数值模拟中参数的选取是合理的，建立的模型可以反应加筋土挡墙在顶部均布条形荷载作用下的受力、变形规律，可为后续深入的研究奠定基础。

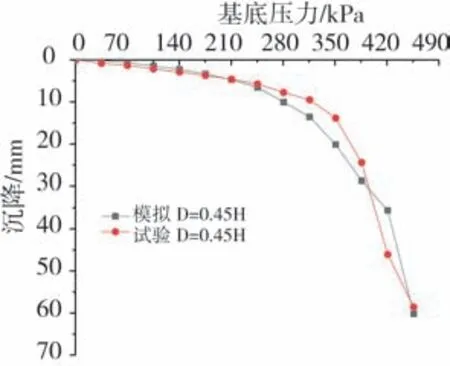
图3 条形基础在竖向荷载作用下沉降曲线Fig.3 Settlement curve of strip foundation under vertical load

2 结果分析

为探讨倒梯形布筋方式加筋土挡墙的力学特性，在数值模型中通过改变基础偏移距离D（D=0.15H、0.25 H、0.35 H、0.45 H、0.55 H、0.65 H、0.75 H）来分析加筋土挡墙的工作性能，探讨基础偏移距离D对条形基础的极限承载力、挡墙面板水平位移、筋材拉应力分布以及挡墙潜在破裂面的影响。

2.1 条形基础的极限承载力

图4为倒梯形布筋方式的加筋土挡墙在墙顶竖向荷载作用下条形基础的基底压力与沉降关系曲线。由于各曲线的发展趋势大致相同，因此以基础偏移距离D=0.45 H的加筋挡墙为例来分析倒梯形加筋土挡墙在竖向荷载作用下的基底压力与沉降关系曲线的变化趋势。从图4中曲线的发展趋势，大致可分为4个阶段：第1个阶段为初始压密阶段，在第一级荷载（35 kPa）作用下，条形基础的沉降主要是由土体受压密实引起；第2阶段为承载力发展阶段，当荷载从35 kPa增大到175 kPa，基础的沉降量线性增加，挡墙的承载力逐渐得到发挥；第3阶段为挡墙的屈服阶段，当竖向荷载从175 kPa继续增大的过程中，曲线的斜率逐渐增大，曲线明显变陡，条形基础的沉降量显著增加；第4阶段为挡墙失稳破坏阶段，当荷载超过挡墙的极限荷载时，基础沉降量急剧增加，最后倾斜失稳破坏，以挡墙破坏前一级荷载作为挡墙基础的极限荷载，也称基础的极限承载力。

采用Cerato［21］的建议，将加筋地基浅基础沉降量的0.1 b（b为基础宽度）对应的荷载作为浅基础的承载力。本文条形基础宽度为0.15 m，对应的沉降量为15 mm，通过图4中虚线与不同基础偏移距离D下的沉降曲线相交，得到基础沉降量为15 mm对应的基础承载力绘制在表5中。根据表5可知，0.1 b沉降量对应的基础承载力随着基础偏移距离D的增加表现出先增加后减小的变化规律，在基础偏移距离D=0.45 H时，此时基础承载力达到最大，为323 kPa。

此外，由图4及表5可知，D/H=0.35～0.55时，基础的极限承载力相同，而0.1 b沉降量对应的基础承载力分别为306 kPa、323 kPa、287 kPa，以及基础的最终沉降量分别为75 mm、60 mm、61 mm，通过对比发现基础偏移距离D=0.45 H时，基础的极限承载力及0.1 b沉降量对应的基础承载力均为最大，且基础的最终沉降量最小，故由此可得到基础的最佳偏移距离为0.45 H。

表5 不同基础偏移距离0.1 b沉降量的基础承载力Table 5 Bearing capacity of foundation with different foundation offset distance 0.1 b settlement

图4 条形基础基底压力-沉降曲线图Fig.4 Curves of pressure and settlement of strip foundation

2.2 加筋挡墙面板水平位移

对加筋土挡墙数值模型的挡墙面板沿墙高度布置6个监测点，从上到下分别为h1～h6，转化成相对墙高h/H分别为0.95、0.77、0.59、0.41、0.23、0.05，挡墙面板在竖向荷载作用下的水平位移情况如图5所示。从图5可以发现，在数值模型破坏之前，面板的侧向位移随着竖向条形荷载的增大而增加；在数值模型破坏时，挡墙面板的侧向位移及变形情况随着条形荷载作用位置的不同而表现出差异性。加筋土挡墙在顶部承受条形基础荷载作用时，当D/H＜0.45时，挡墙面板顶部的侧向位移明显大于挡墙其他监测点的位移，呈现“上部位移大，下部位移小”的特点。当D/H=0.45时，在墙顶条形荷载较小时，挡墙面板的水平位移表现出常规加筋土挡墙“中部位移大，顶部及底部位移小”的趋势，随着条形荷载继续增大，挡墙面板最大水平位移逐渐从挡墙中部向挡墙顶部转变，这主要是因为前期墙顶条形荷载较小且其他层的筋材长度相对于墙顶首层筋材依次递减，使得其他层筋材的加筋作用明显弱于顶层筋材，后期随着荷载继续增大到极限荷载，顶层筋材的加筋作用得到进一步发挥，使得基底附加压力很好扩散，从而导致挡墙面板的最大水平位移从挡墙中部向挡墙顶部转变。随着D/H进一步增大到0.55、0.65、0.75时，加筋土挡墙面板侧向变化规律与常规加筋土挡墙一致。

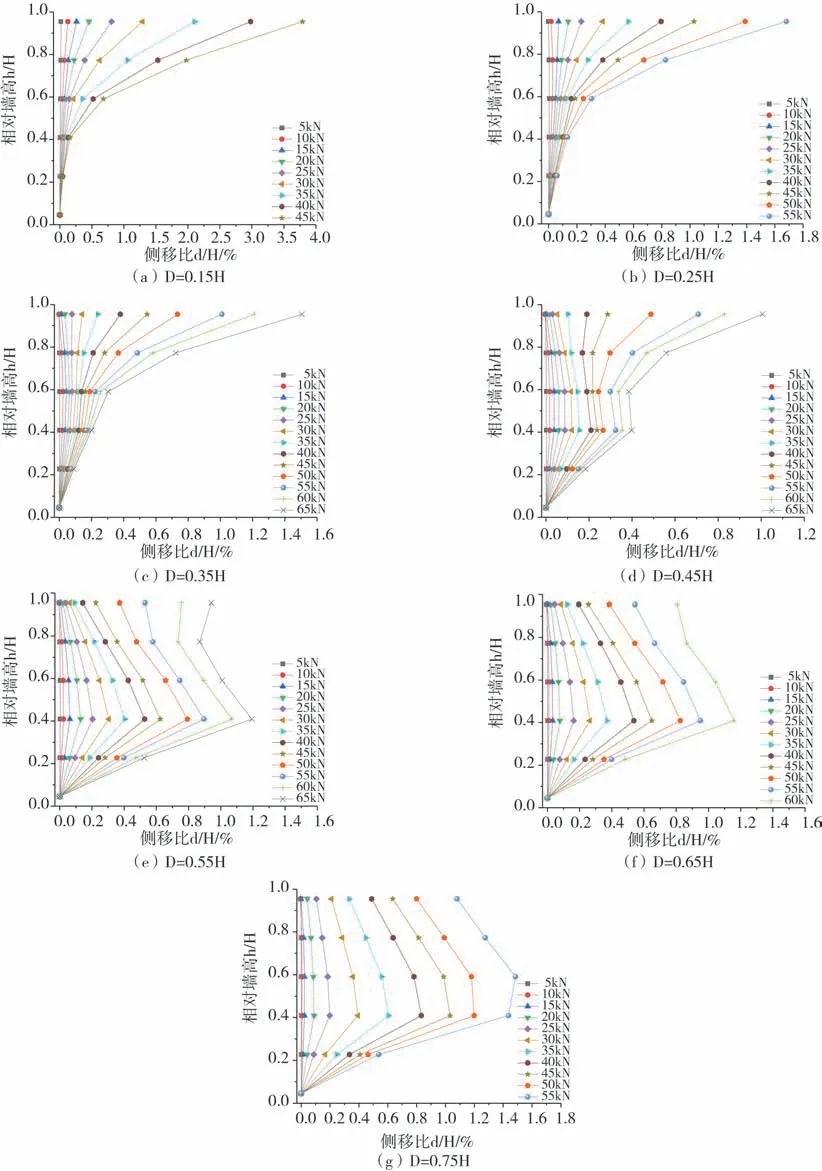
图5 加筋挡墙面板水平位移Fig.5 Horizontal displacement of stiffened retaining wall panel

此外，当D/H≤0.45时，挡墙面板累积最大水平位移均出现在挡墙顶部，挡墙面板最大侧移比d/H（d为面板的水平位移）分别为3.79%、1.68%、1.51%、1.01%，挡墙面板最大水平位移随着基础偏移距离D的增加而减小，且D/H越小，侧向变形越大，达到相同变形所需的竖向荷载越小；当D/H＞0.45时，挡墙面板累积最大水平位移出现在挡墙中部距离墙趾约0.4H（H为挡墙高度），挡墙面板最大侧移比d/H分别为1.19%、1.16%、1.49%，挡墙面板最大水平位移随着基础偏移距离D的增加呈现出先减后增的趋势。

2.3 筋材拉应力分布

倒梯形布筋方式加筋土挡墙在极限荷载作用下的筋材拉应力分布云图，如图6所示。其中4层土工格栅从顶层到底层分别为1～4层，第1层筋材也称为首层筋材。由图6可知，随着条形基础荷载逐渐偏离挡墙面板的过程中，各层筋材的拉应力峰值也渐渐向挡墙内部移动，且各层筋材受到的拉应力在水平方向上均为非线性分布；其中，随着筋材埋置深度的增加，首层筋材的拉应力峰值最大，2～4层筋材的拉应力峰值依次递减。这是因为首层筋材距离条形基础最近，首层土工格栅承担并扩散大部分基底附加应力，此外随着埋深的增加，2～4层土工格栅受基底附加应力的影响逐渐减小。以基础偏移距离D=0.45 H为例，第1、4层筋材的拉应力峰值分别为5.21 MPa、0.72 MPa，两者之间的拉应力峰值约7.2倍左右，说明了土工格栅能很好的扩散基底应力。此外，从图6中不难发现，在不同基础偏移距离D下的加筋土挡墙其土工格栅与挡墙面板的连接处的拉应力远小于各层筋材的拉应力峰值，由此可以说明连接处的格栅强度有足够的安全储备。

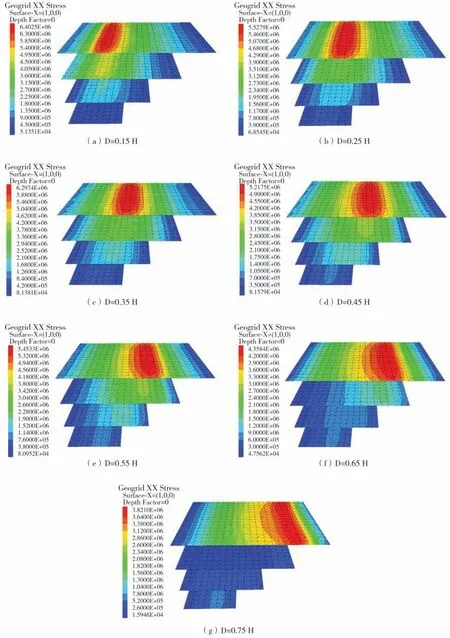
图6 筋材拉应力分布Fig.6 Tensile stress distribution of reinforcement

在改变条形基础偏移距离D的情况下筋材拉应力在水平和竖向方向分布规律一致，本文仅分析基础偏移距离D=0.45 H时加筋土挡墙在竖向均布条形荷载作用下的筋材拉应力云图。由图7可得，随着条形基础荷载的增大，各层筋材的拉应力峰值也随之增加，且各层筋材的拉应力在水平方向上均呈现非线性分布特点，首层筋材的拉应力峰值点出现在条形基础荷载作用的下方，随着筋材埋置深度的增加，2～4层筋材的拉应力峰值渐渐偏移基底中心向面板方向移动。究其原因，由于土工格栅与土体的相互作用能够很好的扩散基底附加应力并向四周扩散，从而导致其他层筋材的拉应力峰值相对于首层筋材拉应力峰值有所降低，以及各层筋材拉应力分布出现差异性。从图7中可以发现，随着条形基础荷载的增加，各层筋材拉应力分布范围进一步扩大，可以看出土工格栅的加筋效果越来越明显，说明土工格栅的加筋作用随着条形荷载的增加渐渐的发挥。

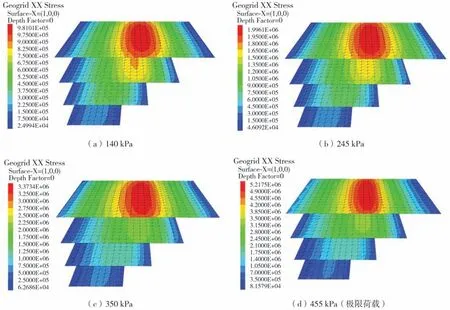
图7 加筋土挡墙筋材拉应力分布（D=0.45 H）Fig.7 Tensile stress distribution of reinforcement in reinforced soil retaining wall under（D=0.45 H）

2.4 加筋挡墙的潜在破裂面分析

图8为倒梯形布筋方式加筋土挡墙潜在破裂面分布图。以筋材最大拉力点的连线分析加筋土挡墙的潜在破裂面［11］，将筋材最大拉力点进行连接，得到加筋土挡墙的潜在破裂面，如图8所示。图8中红色实线为倒梯形加筋土挡墙潜在破裂面，黑色实线为“0.3 H”法理论破裂面。潜在破裂面形状和“0.3 H”法理论破裂面形状表现出一定的差异，表现为潜在破裂面的位置整体向荷载合力作用点方面延伸，这与吴迪［22］等学者得到的结论相一致。随着条形基础荷载远离挡墙面板的过程中，破裂面区域在渐渐扩大，说明倒梯形布筋方式的加筋土挡墙潜在破裂面受条形基础荷载作用位置不同而存在一定的差异。

图8 加筋土挡墙潜在破裂面分布Fig.8 Distribution of potential fracture surface of reinforced soil retaining wall

采用拟合函数y=aebx对倒梯形加筋土挡墙1～4层筋材最大拉力点进行非线性拟合，结果如图9所示。其中1～4层筋材距挡墙底部的距离依次为Z1～Z4，转化成相对墙高Z/H分别为0.82、0.64、0.45、0.27；I为筋材最大拉力点距挡墙面板的距离，用相对位置I/H表示。由图9可知，加筋土挡墙的潜在破裂面随着基础偏移距离D的增加，潜在破坏区域也渐渐扩大，但破裂面形式基本保持一致，其中基础偏移距离D/H=0.15时，挡墙潜在破裂面距离挡墙面板最近，当D/H=0.75时，挡墙潜在破裂面距离挡墙面板最远。将不同基础偏移距离D下的拟合参数绘制到表6中，由表6可知，拟合相关系数R2均在0.9以上，说明拟合结果具有较好的可靠度，加筋土挡墙的潜在破裂面可用指数型曲线表示。