半结构化环境稀疏点云可通行区域检测方法
2022-09-21陈耀忠陆建峰
洪 洋,袁 夏,高 飞,成 诚,杨 欢,陈耀忠,陆建峰
1.南京理工大学,南京210094
2.海装上海局驻南京地区第四军事代表室,南京210008
3.北方信息控制研究院集团有限公司,南京211100
随着人工智能的发展,机器人市场迎来了爆发式增长,服务机器人由室内走向社区,由高速公路走向城市道路,由结构化环境走向半结构化环境。在半结构化环境中,基于机器人本地计算资源的实时可通行区域检测是一个热门研究领域。半结构化环境中,可通行区域检测算法一般可分为以下四类。
(1)基于网格的方法。早期有学者直接利用网格高度信息检测可通行区域的算法[1]。随后有学者把网格方法与其他算法结合来检测地面,例如基于条件随机场的算法[2]和基于时空条件随机场的算法[3]。为了提高算法实时性,李广敬[4]以及李炯[5]等提出基于栅格的快速检测方法。这类方法使用网格,将非结构化点云转为结构化数据,但是点云数据的局部信息被严重压缩,且当障碍物较低或较小时,网格内数据都将被标记为地面,因此该类算法很难检测到高度较低的障碍物,且要求半结构化环境中点云数据密度较大。
(2)基于模型的方法。这类算法主要是基于RANSAC提取环境中平面特征,例如Awwad[6]和魏英姿[7]拟合地平面算法。Chen等提出了基于高斯的实时地面分割算法[8]。为了解决环境中上下坡问题,Patiphon[9]、Zermas[10]以及Bo等[11]提出了基于RANSAC多区域拟合算法。这类算法被广泛应用于半结构化和结构化环境中,但是RANSAC中用来区分局内、局外点的阈值不容易设定,较低障碍物和地面很难区分;同时RANSAC 算法从一个数据集中只能估计一个模型,现实中的地面并不是一个完美平面或几个平面简单拼接的结果,因此这类算法依旧难以适应非平坦地面。
(3)基于点位置分布特征的方法。Himmelsbach 提出了基于射线的地面分割方法[12]。Vo 提出区域增长分割算法[13]。段建民[14]以及苏志远[15]利用环境特征检测城市半结构化道路。这类算法虽然可以很精准地检测到高度较低的障碍物,但是不适应颠簸环境,颠簸或斜坡环境改变了点云数据的空间分布特征,例如密度、距离、高度等,因此该类算法会带来较多的误检测问题。
(4)近年来基于深度学习的可通行区域检测方法越来越受到关注。例如Velas 使用卷积神经网络分割地面[16]。但深度学习模型对计算资源要求较高,且需要标注大量数据集,在实验中基于公开数据集训练的模型对真实环境的泛化能力仍有待提升。基于深度学习技术的算法模型目前侧重于模型研究,以及在云计算环境下进行部署,多数模型难以完全依靠移动机器人自身的计算资源在本地实时运行。
针对半结构化环境,本文提出一种基于稀疏三维点云的快速可通行区域检测算法,从两个方面处理当前算法所面临的问题。(1)本文算法避免直接使用点云高度特征,转而使用点云直线特征检测结构化障碍物,因此上下坡、颠簸等环境不影响本文算法。(2)通过宽广的角度约束,提取环境中非结构化障碍物,降低了较低障碍物和地面之间相互误检测。
本文工作主要贡献:(1)针对半结构化环境,算法从两个方向出发,区别处理结构化障碍物和非结构化障碍物,使得算法可以适应较为复杂的半结构化环境。(2)一般性算法难以检测路缘石、台阶等较低障碍物,本文算法充分利用环境中的结构化信息,能稳定检测路缘石、台阶等较低障碍物。(3)算法避免了直接使用点云的高度特征,可以适应上下坡、颠簸等情况,同时算法且具备检测负障碍的能力。(4)算法不仅标记出环境中障碍物,而且给出了可通行区域,同时可以在小型移动机器人平台上依靠本地计算资源实时运行。
1 算法框架
本文算法步骤框图如图1所示:首先将无序点云转有序点云,从中快速提取近似直线特征;然后分类直线特征以及提取有效直线特征;结合直线特征检测结构化障碍物和非结构化障碍物;最后标记出环境中的可通行区域,并构建成环境栅格地图。

图1 算法框图Fig.1 Algorithm block diagram
2 直线特征提取
2.1 实验数据
本文实验数据来自于Velodyne-16 激光雷达,该雷达位置相对地面高度38 cm,每帧点云数据由16条环形扫描线组成,具有360°水平视场,水平角度分辨率约0.18°,±15°的垂直视场,垂直角度分辨率2°,机器人实验平台如图2(a)所示。本文参考坐标系为雷达坐标系,即X轴向前、Y轴向左、Z轴向上。本文处理的对象为点云中的1~8 条扫描线,且投影到XY平面,如图2(b)所示。

图2 实验数据说明Fig.2 Experimental platform description
点云预处理方法可以借鉴LeGO-LOAM[17]和LOAM算法[18],包括点云运动畸变校正、无序点云转有序点云。校正点云的运动畸变,将会使本文算法得到更好的实验效果。
2.2 直线特征提取
由于环境中障碍物的尺寸不同,因此点云中结构化障碍物对应的直线段长度也大小不一。在初始阶段将待提取直线特征最小长度设置在较小范围,尽可能多地提取直线段,有利于降低漏检情况。本文将直线段最小长度设置为25 cm。点云中存在的直线特征并不是绝对的直线,主要表现在以下三种情况:(1)激光雷达处在水平面上,点云由环形扫描线组成,当扫面线半径很大时,可以将连续的数个点近似看作直线段;(2)当雷达相对地面高度较低时,环形扫描线在平缓起伏的地面也近似直线段;(3)激光雷达测距有一定的误差,同一直线段上的点不会绝对对齐。
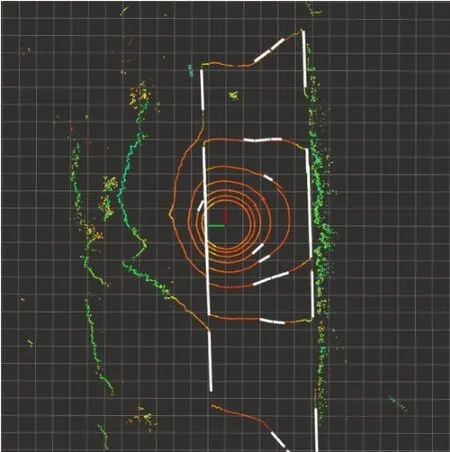
通过以上分析发现,在点云数据中精准地提取所有直线段是比较困难的,因此,本文算法使用模糊线段来提取直线特征。模糊线段(blurred segment)定义[19]:离散直线L(a,b,u,w)是一个整数离散点集(x,y)的集合,该点集满足u≤ax-by 图3 直线特征提取算法框图Fig.3 Block diagram of line feature extraction 存储满足以上约束条件的近似直线段,包括直线段的索引、端点、斜率、截距。雷达是顺时针方向扫描的,直线段起始点位置都是在终止点位置的逆时针方向,因此直线段的斜率用直线与Y轴正方向的夹角来表示,范围是0°~360°。这里的直线截距是直线与Y轴交点坐标,当直线和Y轴近似平行时,直线截距会出现极大或者极小值的情况,因此需要设置直线的最大截距和最小截距,分别为Bmax、Bmin。当直线和Y轴平行时,规定直线的截距等于Bmax。提取直线特征的方法原理简单,提取直线特征结果如图4中白色直线段所示。 图4 直线特征提取结果Fig.4 Extract lines from point clouds 结构化障碍物都有一定的长度以及高度,因此,同一个结构化障碍物表面上的直线段特征会有多条,这一类直线段都有相似的属性,即斜率和截距。因此可以借助聚类方法,将上一章中提取的近似直线段分类,使同一障碍物对应的直线段属于同一个类别,本文使用的是k均值聚类算法(K-means clustering algorithm)。算法框图如图5所示。 图5 聚类算法框图Fig.5 Block diagram of clustering algorithm (1)对直线斜率进行聚类,聚类数目和聚类中心分别为式(2)和(3),聚类后可得到I个簇,但是角度是循环数据,例如0°和360°属于同一个聚类,因此,需要将聚类中心在0°和360°附近的簇合并成一个簇,聚类结果表示为CA。 斜率的聚类数目: 斜率的初始聚类中心ci: 其中,N为直线段总数目,I为整数,直线段总数目是类别5倍。即将360°分成I份,ci是第i份的初始聚类中心。 (2)对直线的截距进行聚类,需要在CA中每个簇内都进行一次对截距的聚类。设Ci中所有直线的最大截距(单位:m)为Bt_max,最小截距为Bt_min,Ck∈CAB,聚类数目和聚类中心分别为式(4)和(5),将Ci聚类后,可以得到K个簇,将聚类中心在Bmax和Bmin附近的簇合并成一个簇。最终聚类结果表示为CAB。 Ci中截距的聚类数目: Ci中截距的初始聚类中心: 其中,K是整数。即在簇Ci中,将直线间的最大截距差分成K份,ck是第k份的初始聚类中心。 在第2章中提取的近似直线段,除了包含障碍物表面上真实的直线段以外,也包含非障碍物表面上无效的直线段,例如半径较大扫描线上的圆弧。这些无效直线段也是聚类的对象,因此需要剔除这些无效直线段。分为以下两种情况。 (1)非障碍物表面上的近似直线段的斜率和截距是没有规律的,因此这些无效直线段所属类别中的样本数目也是极少的。如图6(a)所示,无效直线段所构成的类别分布如图中C1、C2所示,有效直线段所构成的类别分布如图中C3、C4所示,C1,C2,C3,C4∈CAB。因此,当聚类Ck中直线样本数只有1时,那么Ck包含的直线段都是无效的,Ck∈CAB。 (2)如图6(b)所示,有些无效直线段所构成的类别分布也会如图中C1、C2所示,C1,C2∈CAB。这些无效直线段由于环境原因,恰好被聚集在同一个聚类中。本文2.2 节提取的直线特征保留了方向信息,因此本文的直线段特征是有向线段,线段的起始端点都在终止端点的逆时针方向。如图6(b)中所示,类别C1包含两条有向直线段AB、CD,连接AB起始点A 和CD终止点D点,得到新向量AD,同理可以得到新向量CB,从而可以计算出AD和CB之间的夹角α。 如图6(b)所示,C1中夹角α是一个比较大的角度,同理,计算得到C2中夹角α也是一个比较大的角度。而C3中的夹角α值却接近于0。即同一类别中包含两条以上有向直线段,用两条有向直线段重新组织成两个向量,当两向量间夹角α>α0时,表明该这两条直线特征无效。直线特征筛选结果如图6(c)、(d)所示。 图6 直线特征筛选Fig.6 Lines selection 在第3章中,使斜率和截距近似的直线特征属于同一个类别,并且认为该类别中的直线特征都属于同一个障碍物。但是当两个结构化障碍物表面近似平行时,这两个障碍物对应的直线特征斜率和截距也是近似的,那么两个障碍物对应的直线特征将会被聚到一个类别中,例如图7(a)所示,在类别Ck中,Ck∈CAB,如果存在空间位置相邻的两条直线段CD、EF,CD位于扫描线u上,EF位于扫描线m上,且有| |u-m >1,此时直线特征CD、EF显然不属于同一个障碍物。 图7 聚类再分析Fig.7 Cluster reanalysis 当算法检测出道路的两个边缘时,也可以根据两个边缘计算出当前环境下的道路宽度。当道路宽度可用,且点D、E 间的长度大于道路宽度时,Ck也会被重新分成两个新聚类。本节最终的目的是使每一个类别Ck中都只对应一个或者零个障碍物,以方便在第4章中使用它们。 实际中,一个障碍物表面结构一般是连续的,但由于点云数据的稀疏性,障碍物并没有被点云完整地覆盖,因此算法检测到的障碍物是断断续续、不完整的。一般算法检测可通行区域时,往往忽略了障碍物之间的相关性,算法中并没有体现出结构化特征。如图8(a)所示,Ck中包含三条直线特征,Ck∈CAB,三条直线特征对应着同一障碍物,这就意味着从A 点到F 点,都是障碍物实体,但是由于点云数据比较稀疏,使得B 点到C点、D点到E点间都是可以通行的。 为了体现障碍物更完整的结构化信息,可以依次连接Ck中各条直线特征,Ck∈CAB,得到的结果如图8(b)所示。即使在交叉路口等环境下,也可以直接连接每个聚类中的直线特征,因为4.1 节中,使每一个类别Ck中都只对应一个或者零个障碍物。实验结果如图8(c)、(d)所示。 图8 结构化障碍物检测Fig.8 Structured obstacle detection 如图9(a)所示,当算法检测到结构化障碍物AB、CD时,显然,直线AB、CD是不可通行的,由于视角遮挡,区域S1、S2的可通行性是未知的。从应用层次的角度的来分析,区域S1和S2不属于可通行区域。 为了快速检测区域S1、S2,本文使用快速排斥实验和跨立实验。如图9(b)所示,直线特征AB是一障碍物的边界信息,点云数据中任意一点pi,连接原点和pi得到向量Opi。当AB和Opi相交时,即可判定点pi属于不可通行区域。实验结果如图9(c)、(d)所示。 图9 不可通行区域检测Fig.9 Detection of inaccessible areas 当图9(a)中白色区域存在非结构化障碍物时,这种情况并没有得到有效的处理。本节通过地面最大倾斜约束条件,来检测非结构化障碍物。根据《城市道路设计规范》《汽车库建筑设计规范》,以及《城市居住区规划设计规范》等规定,在半结构化环境中,地面的倾斜度一般不大于15°,考虑颠簸等情况,本文把地面最大倾斜度设置为σ=20°。 首先将点云数据由扫描线形式,重新组织成射线形式,如图10(a)所示,相邻射线之间的夹角为0.18°,共有2 000条射线,理论上每条射线包含16个节点,每个节点代表点云数据中的一个点。但是当一束激光反射点非常远或者没有反射时,该节点缺失。 本文把点云射线和障碍物相交的点,称之为截至点。当射线遇到截至点时,射线会被截断,即射线不包含区域S1、S2的点。既减少了算法的计算量,又降低了障碍物检测对本节算法的依赖程度。 然后计算每一条射线上相邻点之间的夹角,如图10(b)所示,点pi和点pi+1是同一射线上相邻点,坐标分别为(xi,yi,zi)、(xi+1,yi+1,zi+1),两点之间夹角θ: 图10 非结构化障碍物检测原理Fig.10 Principle of unstructured obstacle detection 当夹角θ>σ时,将pi+1标记为障碍点,当点pi+1缺失时,依次用点pi+j来替代pi+1,j=2,3,4,j<5。实验结果如图11所示。 图11 非结构化障碍物检测Fig.11 Unstructured obstacle detection 将4.2节、4.3节实验结合,叠加两部分检测结果,剔除重复的障碍点,便可得到最终的实验结果。如图12(a)所示,其中彩色代表原始点云,白色点代表障碍物。按照4.3节实验方法,将图12(a)中不可通行区域填充后并表示为栅格地图,效果如图12(b)所示。 图12 可通行区域Fig.12 Results of traversable area 在实验结果分析中,本文算法将与文献[9]算法、LeGO-LOAM 算法[17]地面分割部分进行对比。文献[9]算法通过分析点云几何结构和RANSAC多平面拟合的方法来检测地面,该算法适用于斜坡环境中的三维点云地面分割方法。文献[17]算法将点云数据投影成二维图像,基于图像的方法完成地面分割。本文算法中的实验参数具体设置如下:n=5,α0=8°,σ=20°,Bmax=36 m,Bmin=-36 m。 算法的实时性,是评估算法实用价值的重要标准之一。本文算法在ROS环境中,使用C++实现,可以在Intel NUC 迷你电脑上运行并实时检测可通行区域,系统的具体参数如表1 所示。系统实时性要求算法完全依靠移动机器人自身的计算资源在本地实时运行,因为激光雷达数据输出频率为10 Hz,因此算法运行时间必须小于0.1 s。 表1 系统信息Table 1 System information 本文结合了7 100 帧点云数据,在平坦道路、弯道、斜坡等多种环境下,测试了上述三个算法运行时长,如图13 所示。本文算法平均运行时间是0.014 s,最大时长为0.041 s,最小运行时长为0.006 s,本文算法完全可以达到实时性要求。 图13 算法运行时间Fig.13 Run time of algorithms 如图14(a)所示,该场景下包含负障碍物,蓝色框中是没有井盖的地下管道入口,井口的尺寸约为0.6 m×0.4 m。如图14(b)、(d)所示,当激光雷达到负障碍的距离约2 m时(本文实验平台尺寸为0.5 m×0.5 m),文献[9]算法和本文算法可以稳定地标记出负障碍物,同时,本文算法可以准确地标记出路缘石等障碍物。文献[17]算法并不具有检测负障碍物的能力,且和激光雷达到负障碍的距离无关。实验结果说明,本文算法具有检测负障碍物的能力。 图14 负障碍场景实验结果Fig.14 Results of negative obstacle scene 平坦实验场景如图15,在(a)、(i)、(m)中,检测较矮的障碍物方面,本文算法实验结果都要远好于文献[9]算法和文献[17]算法。在直道试验场景图15(a)中,本文算法可以准确提供道路的边缘信息,在转弯实验场景图15(i)中,本文算法更准确标记出了道路的轮廓,标记效果要远好于文献[9]算法、文献[17]算法。场景图15(m)表明环境中的车辆、行人等因素对本文算法影响较小。同时,在图15(d)、(l)、(p)中,说明了本文算法可以准确地补充障碍表面信息,更好地体现了障碍物结构化信息,更能体现可通行区域的概念。在车库实验场景图15(e)中,环境中的障碍物高度都比较高,三个算法的实验结果近似,没有太大的差异。 图15 平坦场景实验结果Fig.15 Results of flat scenes 斜坡在环境中主要表现为上下坡道,移动机器人在上坡过程中,主要有上坡前、上坡后两个环节。移动机器人在下坡过程中也有下坡前、下坡后两个环节。这4个环节分别对应场景图16(a)、(e)、(i)、(m)。虽然文献[9]算法针对斜坡环境使用了基于RANSAC多平面拟合方法,但是该算法在上坡过程中,依旧将较远距离的斜坡地面标记成障碍物,如图16(b)、(f)所示,当然文献[9]算法对所有帧的测试结果并不都是如此,但是算法误检测的概率也将近30%,因为文献[9]算法中并不能保证它划分的多个区域正确。文献[9]算法和文献[17]算法实验结果近似,但是文献[9]算法在障碍物和非障碍物交界处的实验结果一般,如图16(n)所示,文献[9]算法将部分地面检测成障碍物。而本文算法是结合直线特征来完成的,在半结构化环境中,本文算法的适应性要比文献[9]算法和文献[17]算法更好。 图16 斜坡场景实验结果Fig.16 Results of slope scenes 本文结合半结构化环境特征,提出了一种实时可通行区域检测算法。该算法将可通行区域检测问题分解成了两个任务,即结构化障碍物和非结构化障碍物检测,避免了直接利用点云的高度信息,从而能更好地适应斜坡、颠簸、负障碍等环境。该算法可以在中小型AGV上实时运行,适用于低密度点云,在后续的局部路径规划和目标分类中,具有一定实用价值。在接下来的研究中,将利用多帧数据间的时间关联性进一步提高算法的鲁棒性。

3 直线特征分类和筛选
3.1 直线特征聚类




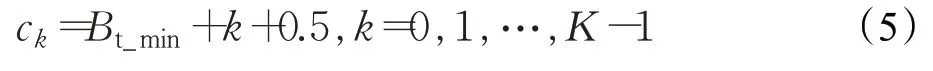
3.2 直线特征筛选


4 可通行区域检测
4.1 聚类再分析


4.2 结构化障碍物检测

4.3 非结构化障碍物检测




4.4 可通行区域

5 实验与分析
5.1 算法效率


5.2 负障碍环境测试

5.3 平坦环境测试

5.4 斜坡环境测试

6 结束语
