过必经点集且具有额外硬约束的最短路径算法
2022-09-21郭展羽张志明贺兰山郑家齐赵师兵
郭展羽,张志明,贺兰山,郑家齐,赵师兵,康 琦
同济大学 电子与信息工程学院,上海200092
最短路径问题一直是运筹学、计算机科学、地理信息科学、交通运输等领域的研究热点,并广泛应用到公共交通运输网络规划、无人自动驾驶、机器人自主导航等的实际问题中[1-6]。现实生活里有许多问题都可以抽象转化为最短路径问题,路径规划要求根据某种优化准则,在给定的真实环境中寻找到一条从起始位置到目标位置可行并且代价最小的路径。研究如何有效地计算和求解最短路径问题,其面临的难点是如何在较短的时间内找到较为完备的解。根据对环境信息的掌握程度不同,路径规划可分为全局路径规划和局部路径规划,两者没有本质上的区别。经典的全局路径规划算法有Dijkstra算法[7]和A*算法[8]等,可以静态地规划出最优或次优路线。近年来,国内外学者在此基础上,引入启发式算法和仿生算法等,提出多种最短路径改进算法[9-16],如模拟退火法、蚁群算法、遗传算法、粒子群算法、深度优先算法和广度优先算法等,并在解决过必经点集的最短路径问题上已经取得很好的成效,康文雄等人[9]通过分层回溯的Dijkstra 算法,有效地减少问题求解的计算时间;Daniele 等人[10]对约束最短路径漫游问题(constrained shortest path tour problem,CSPTP)提出新的数学模型和高效的分支定界方法;王磊等人[14]使用改进的A*算法,对最短路径段进行拼接,使运算效率得到显著提高。
在探究路径规划算法的过程中,应用场景由于物理条件的限制会存在额外硬约束条件,而上述算法在处理此类问题时,往往需要简化前置条件,忽略硬约束,导致实际解算过程中会存在求解难度高、求解速度慢、求解结果不可靠甚至不可行等的不足,需要做出相应改进。本文以第十五届全国大学生智能车竞赛室外光电组总决赛实车比赛[17]为例,将比赛赛道抽象建模为无向带权图表示,提出一种基于深度优先搜索的随机搜索算法,以解决具有额外硬约束条件下过必经点集的最短路径问题。该算法的创新点在于,搜索过程中对路径的可行性加入额外硬约束条件进行实时判定,在给定的真实环境中最终寻找到过必经点集的最优或次优的最短路径。
1 问题描述
1.1 背景
第十五届全国大学生智能车竞赛室外光电组总决赛采用G型等比缩小的无人车模,场景化地复现人工智能在实际领域中的应用。无人车在长宽17 m×10.5 m大小的场地内进行比赛,赛道由若干区域连通而成,分布如图1(a)和图1(b)中所示。比赛要求无人车从起点区域处出发并开始计时,规划合理的路径,经过赛道上若干所有指定的区域后到达指定终点区域,停止计时并判定完赛,最终的比赛成绩按完成时间进行排名;无人车在未经过所有指定区域之前到达终点,不会停止计时。起点区域、终点区域,以及中途要经过的若干区域和无人车的发车方向,在比赛开始前随机指定给出。无人车在运行途中可以多次通过赛场中的某个赛道区域,且经过随机指定区域的先后顺序不限,但需要至少穿过一次指定区域。
本文即在此背景下展开工作,解算无人车在给定起点和终点之间的最短路径。举例如下:如图1(b)中所示,设比赛要求从起点(start)vs=1出发,经过指定区域(pass)vp={2,7,10}后到达终点(destination)vd=6。通过直接观察可以得出最优解,即路径1→2→10→7→6为最短路径,如图1(c)中所示;该赛道可以建模抽象为无向带权图如图1(d)中所示。然而,在面临比赛现场更加复杂的环境要素时,需要将该最短路径问题建立合适的数学模型,引入硬约束条件后,设计合适的算法,才能进行快速且完备的求解。
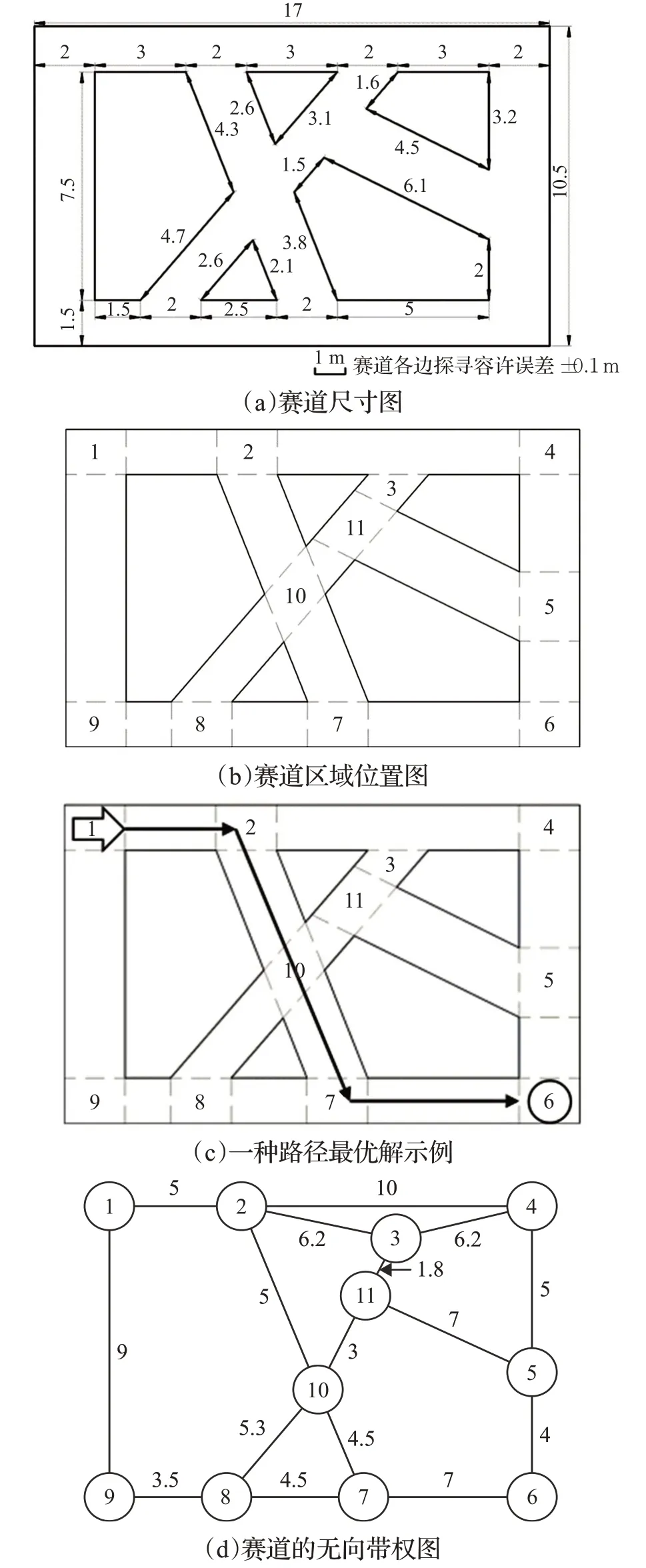
图1 应用场景示意图Fig.1 Schematic diagram of match field
1.2 建模
图1 所示的赛道区域位置图可以抽象成一个无向带权图,权值即为赛道图中点与点之间的路程距离。假设无人车在各段赛道上的行驶速度一致,则可以将时间最优化目标转换为总路程最优化目标,将该问题抽象为过必经点集的最短路径问题。与此同时,本次最优化问题还存在有额外的硬约束:无人车ART-RC底盘机械尺寸为560 mm(长)×350 mm(宽)×230 mm(高),由于赛道宽度的限制,使得无人车无法调头行驶,即路径中不能存在包含相邻节点的子路径A→B→A(设A、B 为相邻节点);由于无人车车模转弯半径的物理条件限制,无人车在实际赛道上无法转过转角小于90°的弯道(锐角弯,即急弯,下文称为“锐角弯”),如对于图1(b)中的路径8→7→10,无人车无法通过,但路径8→7和7→10,在无向带权图(d)中存在,且不能通过预处理的方法将该路径从图中剔除。
依据上文所述优化目标和约束条件,可以转化为如下给定的一个无向带权图G(P,E) 数学模型,其中P={p1,p2,…,pn}为节点集,E={e1,e2,…,en}为无向边集,设ωij为连接pi节点和pj节点的无向边的权值。必经点集P′⊆P-{s,d},其中s和d分别为路径规划的起点和终点。硬约束条件边集H,其内部的边元素由前中后三个节点构成,如上文所举例的{8,7,10}。最短路径可以有两种等价的表示形式:以节点集描述的最短路径Wp={pa,pb,…,px,py}和以无向边集描述的最短路径We={eab,ebc,…,exy}。求解满足以下约束条件的优化目标函数获得最短路径。

其中,式(1)表明以路径最短为优化目标;式(2)为约束条件之一,要求路径Wp经过必经点集P′中的每一个节点;式(3)为约束条件之二,要求路径满足额外硬约束条件。
因此,在求解过必经点集的最短路径问题的过程中,受到如上文所述额外硬约束的限制。为了便于程序处理并计算数据,将抽象出来的无向带权图转化为二维邻接矩阵,矩阵中存有图中任意相邻两点之间的距离。当两点不是相邻时,距离值设为-1;点与其自身的距离值设为0。
1.3 变量定义
定义算法中的相关变量,如表1中所示。设定算法中路径规划的起点节点start、面朝点节点next(小车运行方向前方选择的后一个节点,从起点出发时即为所选择经过的第一个节点)、必经点集point_list[]和终点所在节点区域destination等,根据这些参数计算出一条可行的最优路径;在计算的过程中,分别定义当前搜索到的路径way[]、已知路径当中的最短路径temp_way[]和最终的最优最短路径shortest_way[];无向带正权图的所有信息保存到一个二维邻接矩阵dis[][]。
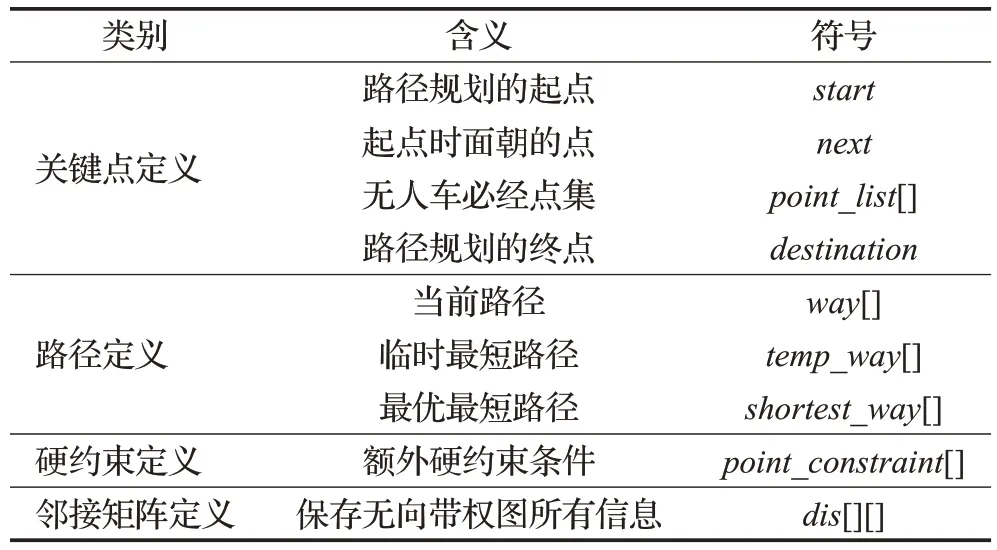
表1 变量定义1Table 1 Variable definition in algorithm,part 1
额外硬约束(“point_constraint”):将指定的额外硬约束条件存放在一个列表当中,作为参数进行设定,在进行路径搜索时,对搜索得出的解进行是否满足额外硬约束的判定,即判断解路径中是否含有额外硬约束当中的子路径。硬约束使用连续三个点作为约束,中点作为索引,如在图1中,路径2→3→11为不可通行的锐角弯,故point_constraint[3]中含有[2,3,11];路径3→11→5 也是不可通行的锐角弯,故point_constraint[11]中含有[3,11,5],以此类推。将完整的硬约束提前设定好,供搜索时使用。
2 算法实现
算法主要分为预处理和核心算法两个部分实现。预处理阶段通过一定的步骤,将使用者输入的信息转化为后续阶段核心算法所需要的信息,完成对问题的无向带权图的处理和建模。核心算法部分则使用基于深度优先的随机搜索算法,在满足额外硬约束的要求下,求解过必经点集的最短路径问题。
2.1 预处理
2.1.1 输入参数
通过程序输入起点start、起点时的面朝点next、终点destination和存放在point_list[]当中的必经点序号列表,额外硬约束条件由point_constraint[]变量载入,图的信息以邻接矩阵的形式存放在文件当中读入。
2.1.2 相邻点查找函数
输入的邻接矩阵仅仅描述了各点之间的距离,预处理时使用查找函数寻找遍历各节点位置上的所有相邻点,算法流程如图2所示,具体步骤列举如下:

图2 相邻点查找算法流程图Fig.2 Flow chart of adjacent point set search algorithm
(1)得到图的大小,创建合适的数据结构变量存储各点的相邻点信息,首先求得图中节点的个数length,然后以维度为length的一个列表对象用以存储变量。
(2)对图中任意未遍历的点进行探索,判断其与其余点的距离,如果距离大于0,则代表两点相邻,将后点加入前点的相邻点列表。
(3)重复步骤(2),直到图中所有的点均被遍历。
(4)最后得到完整的相邻点列表choices 并存储。
对于本次赛题,预处理后得到赛道无向带权图中①~⑪各个节点的相邻点列表,具体为[[2,9],[1,3,4,10],[2,4,11],[2,3,5],[4,6,11],[5,7],[6,8,10],[7,9,10],[1,8],[2,7,8,11],[3,5,10]]。
2.1.3 预处理阶段的输出
预处理工作结束后,得到如前所述的各项初始参数:start,next,destination,point_list[],dis[][],choices[]。
2.2 核心算法描述
2.2.1 参数定义
有效路径次数限制(t_limit):使用随机搜索时,需要设置一个上限值来结束路径的查找,每当找到一条符合条件的路径时,有效路径次数(t)加1。次数上限值越高,计算的结果最优性也就越高,但相对的,时间与空间的消耗也就越大。
路径长度限制(L_limit):使用深度优先的随机算法寻找一条路径时,限制路径的长度(L)有助于结束对过长路径做无意义的搜索,可以节省每次路径搜索所耗费的时间和空间,但是相对的,如果受到限制后无法求得解,则需把该限制放宽。这个值不应该大于任意一条能遍历图上所有节点的路径长度的两倍,否则就失去效用。如图1 中的路径1→2→10→7→6→5→4→3→11→10→8→9→1 可以循环遍历所有节点,当起点要求为vs=10,终点要求为vd=1,要经过vp={2,7,6}时,按上文所述的这条路径则需要经过10→7→6→5→4→3→11→10→8→9→1→2→10→7→6→5→4→3→11→10→8→9→1。由此可以得到结论,最多循环走过该条路径两次可以保证该问题有解。
状态定义:在搜索时,每一个状态含有参数的定义:当前点(now),即当前点的序号;当前路径(way[]),即由多次循环当中的多个当前点形成;前点(pre),即当前路径中前一点的序号;当前距离(d),即当前路径总的距离长度。
变量定义总结成表格如表2所示。

表2 变量定义2Table 2 Variable definition in algorithm,part 2
2.2.2 伪代码描述
(1)最短路径求解函数
算法1 最短路径求解

(2)必经点路由判断函数
算法2 必经点路由判断


(3)硬约束条件状态判断函数
算法3 硬约束条件判断

其中变量point_constraint即为本问题中的额外硬约束条件参数,以节点7 为例,point_constraint[7]=[[8,7,10],[10,7,8]],经过判断即可得出该路径的可行性。
2.2.3 算法流程图描述
算法流程图如图3中所示,各步骤简述如下:

图3 核心算法流程图Fig.3 Flow chart of core algorithm
(1)初始化搜索状态,将变量L_limit归零,所有临时路径和节点清空。
(2)随机探索下一个非前点(pre),并更换搜索的状态。探索的方式是从当前点的相邻点列表中,排除前点后随机选择一个。
(3)判断是否到达终点。若否,重复步骤(2)。
(4)判断是否过所有必经点。若否,重复步骤(2)。对必经点集的各点进行逐个判断。
(5)判断是否满足额外硬约束。任意截取长度为3的子路径,判断是否为point_constraint列表中的元素:若是,则不满足额外硬约束;若否,重复步骤(2)。
(6)比较路径长度与已知最短长度,如果当前路径较短则替换为最短路径。
(7)判断是否超过次数限定,若否,重复步骤1。
(8)输出最短路径。
3 实验测试与结果分析
实验测试环境为:Windows 10操作系统,Intel 2.3 GHz i5-8300H CPU,8 GB 内存,编程语言为Python3.7,编程环境为PyCharm Community Edition 2020.2.3。使用第十五届全国大学生智能车竞赛室外光电组总决赛赛题[17]的赛道建模数据进行仿真测试,所获得的最短路径用于实车测试。
3.1 时间效率和最优率的影响因素——必经点集中节点个数
在程序当中设置计时器记录程序运行时间来粗略计算算法的时间效率。在其他点不变的情况下,增加必经点集中节点的个数,每次实验取100次最优输出进行结果平均。此次实验条件为:start=1,next=2,destination=6,t_limit=20,L_limit=20,同时实验结果还必须满足额外的硬约束,即不能转过小于90°的锐角弯赛道且不能倒车。取实验结果的平均值记录在表3。
由实验结果可见,在序号为1、2、3 和序号为4、5 的实验中得到的解算时间结果相差较大,数值不在一个数量级,但最优率都为100%,最优率的问题将留在后续的实验2进行讨论。针对时间结果,经过分析可知求解花费时间较大差异的原因:经过点v={3}的最短路径同时也经过vm={5,7},所以计算时通过随机搜索容易搜索到最优解,而因为vn={9,11}没有出现在此路径中,当需要经过它们的时候,需要更多的时间去搜索。其余实验条件不变的情况下,必经点集选为{3,9},重做实验6验证上述分析,表3中给出实验相关结果。比较实验1、2、3、6的结果,可发现该算法的效率更多地取决于中间节点集的选取,而不是由中间节点的数量决定。由于解算过程中使用随机搜索的算法,同一种实验条件下,不同次实验之间的时间可能会存在比较大的差异,但多次重复实验后得到的时间结果会稳定在一定均值附近范围内。

表3 必经节点集的影响Table 3 Impact of choosing necessary node set
3.2 时间效率和最优率的影响因素——t_limit参数
基于实验1,在仅仅选取3、9 两点时平均需要消耗6.710 s的时间,此时的实验条件中t_limit设为20。将该数值从小到大变化,进行100次实验取实验结果的平均值,将其变化对时间效率和最优率的影响记录在表4,其中最优率为所求路径结果中,最优路径(可能有多种)数量占所有路径结果数量的比率。由表4 中的实验结果可以看出,当t_limit设为较小的数时,计算时间较短,最优率低;当t_limit参数值增大时,运行时间变长,最优率增加;当设为10及以上数值时,最优率可增长到97%以上直至100%。
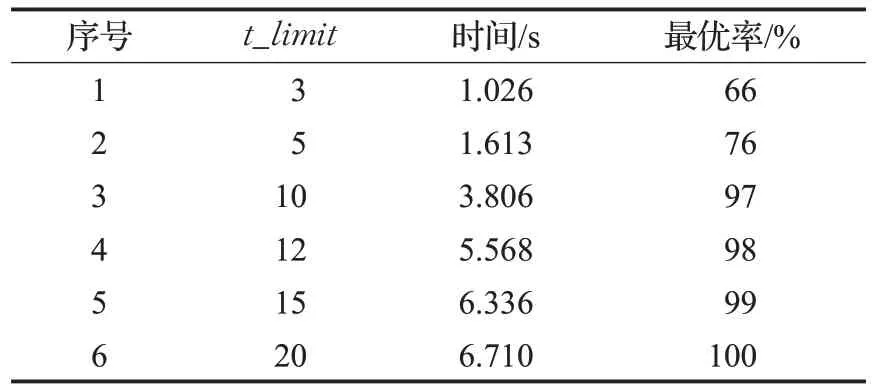
表4 参数t_limit 的影响Table 4 Impact of t_limit parameter
3.3 不同算法对TSP问题求解的效果
本文提出的过必经点集且具有额外硬约束的最短路径搜索算法也可以用以解决旅行商问题(traveling salesman problem,TSP),按如下参数进行初始设置:起点start=1,面朝点next=2,终点destination=1,必经点集point_list=[3,4,5,6,7,8,9,10,11]。和爬山法(hill climbing,HC)、模拟退火法(simulated annealing,SA)、遗传算法(genetic algorithm,GA)等算法[18]做对比实验,实验分别测试100次,取实验结果的平均值,列举如表5中所示。

表5 不同算法效果之间的比较Table 5 Comparison results of different algorithms
从实验结果可以看到,在多种算法之间,爬山法的计算速度最快,遗传算法的计算速度最慢。从理论上分析,这三种传统算法,会牺牲解的质量来提高计算的速度,具体表现为爬山法较其余算法更容易陷入局部最优解。但在本次实验中由于计算规模较小,解的质量差异不明显,在此仅讨论求解时间和最优结果。可以看到前三种传统算法给出的最优结果均是:[1,2,10,11,3,4,5,6,7,8,9],如图4 中虚线所示,很明显,所包含的中间路径[…,2,10,11,…]是不满足额外硬约束的,无人车无法转过此处的赛道转角。而本文提出的算法给出的最优结果是:[1,2,10,7,6,5,4,3,11,10,8,9],如图4中实线所示,其中没有包含违反额外硬约束条件的中间路径,无人车可以顺利完成任务。尽管本文算法在计算时间上不具有绝对的优势,但是可以有针对性地解决具有额外硬约束的过必经点集的最短路径问题。

图4 不同算法求解得到的最短路径示意图Fig.4 Schematic diagram of obtained shortest path
4 结束语
本文对“过必经点集且具有额外硬约束的最短路径问题”进行抽象处理,并提出基于深度优先搜索的随机搜索算法。实验测试表明,该算法具有可以添加额外的硬约束、解的最优性好的优势。由于该算法是采用随机搜索的算法,时间效率上受必经节点数目的影响较小,但受必经节点元素集的选取影响较大,难以得出统一的评判标准。通过TSP问题的求解对比实验,该算法相比于传统算法,尽管在计算时间上不具有绝对的优势,但是针对性地解决具有额外硬约束的过必经点集最短路径问题。该算法的优势在于代码量少、最优性好,可以解决额外硬约束问题,同时容易调整参数。
