结合柯西核的分类型数据密度峰值聚类算法
2022-09-21盛锦超杜明晶李宇蕊孙嘉睿
盛锦超,杜明晶,李宇蕊,孙嘉睿
江苏师范大学 计算机科学与技术学院,江苏 徐州221100
聚类[1]是一种利用数据自身属性进行归类的数据挖掘方法,可以有效处理大量无标注的数据集。聚类过程依赖数据间的距离度量,由于欧式空间的量化性质较好,因此数值型数据一般采用欧氏距离作为度量方法,但这对分类型数据并不适用。分类型数据作为一种常见的离散型数据,数值空间较为复杂。传统基于划分的聚类方法[2]在处理分类型数据过程中往往无法得到良好的划分效果,一方面考虑的距离度量相对简单,比如K-modes(KM)[3]算法所采用的汉明距离度量(Hamming distance measure,HDM)[4]只计算数据对应属性的差异程度,忽视了数据属性的相关性、权重等重要信息;另一方面,基于划分的聚类方法并不能有效捕捉复杂数据的数值分布,例如在属性加权K-modes(weightedK-modes,WKM)[5]、混合属性加权K-modes(mixed weightedKmodes,MWKM)[6]等算法上尽管采用了量化性质更好的距离度量方式,但其聚类效果依然有限。
目前分类型数据距离度量的方法中,一般使用条件概率分布计算数据属性间的关联信息,利用信息熵计算属性的权重,比如OF[7]、Goodall[8]等,但是当前研究很少考虑到分类型数据存在的一个重要特性——有序特性[9]。事实上,分类型数据的属性可以进一步划分为有序型属性和名义型属性,其中有序是指该属性的属性值之间存在顺序关系。例如图1所示,现实情况下讲师与副教授的差距应该小于讲师与教授之间的差距,假如对这个属性进行度量,那么其对应关系的信息也应该得到保留,相反,名义型属性并没有这种顺序关系。EBDM-KM[10]是一种使用信息熵对有序特性进行度量的分类型数据聚类算法,该算法从一定程度上提高了聚类效果。HDNDW[11]同样考虑了数据属性的有序特性,并且该算法将名义型属性转换为有序型属性,统一了分类型数据的内在特性,尽管该算法的聚类表现较好,但是其内部参数计算非常复杂且算法的收敛性较差,很难应用在实际社会生产中。UDMKM[12]进一步提出了利用熵整合属性关联、权重和有序的距离度量方法,但其聚类手段仍局限于传统划分方法,聚类性能提升有限。

图1 职称关系Fig.1 Title relationships
密度峰值聚类(density peaks clustering,DPC)[13]算法是一种有效应对复杂数据分布的密度聚类算法[14],已经广泛运用在工业领域。DPC 根据密度峰值点确定类中心,并将未分配数据分配给比其密度更高且距离其最近的数据所在类中,因而算法执行快速高效,但是其容易受到链式错误的影响且不能很好处理密度分布不均问题。共享最近邻密度峰值聚类算法(shared nearest neighbor density peaks clustering,SNNDPC)[15]通过共享最近邻和二次分配方式解决了数值型数据的链式错误和密度不均问题,王大刚等人[16]则利用二阶K近邻及多步骤的分配策略缓解了数据的不规则、密度不均匀问题,此外,丁世飞等人[17]基于度量优化,柏锷湘[18]使用自然最近邻,赵嘉等人[19]采用相互邻近度都从一定角度出发缓解甚至解决了上述问题,但是这些方法都只针对数值型数据,因而简单地将现有的分类型距离度量引入该算法中,依然无法很好地解决分类型数据的聚类问题。其中最主要的原因为在距离度量方面,现有的距离计算大多会产生“距离值的重叠问题”,例如图2(a)所示在拥有24 个数据的Lenses 数据集上使用HDM 计算数据之间的距离,结果产生了大量相同距离结果值,这往往不利于距离远近的比较。在密度计算方面,上述提出的重叠问题会进一步导致“密度值的聚集问题”,即较多数据有相同密度值的情况,例如图2(b)所示的数据在最终分配过程中其周围数据的密度值相同,最终结果很有可能将该数据分配给一个密度更高但实际距离较远的类中,导致最终的聚类结果变差。
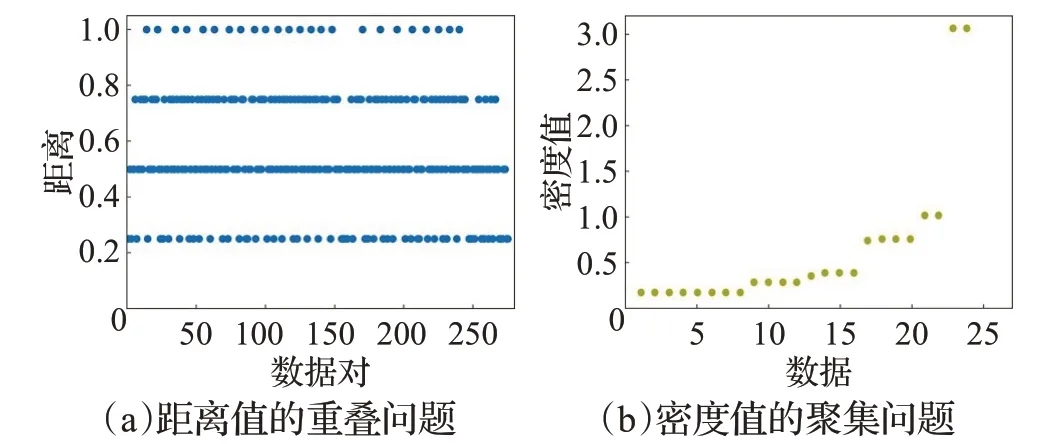
图2 分类型数据在DPC上存在的问题Fig.2 Problems of categorical data on DPC algorithm
考虑到这些问题,本文提出一种改进的结合柯西核的分类型数据密度峰值聚类算法(Cauchy kernel-based density peaks clustering algorithm for categorical data,CDPCD)。算法首先提出了一种新的基于概率分布的加权有序距离度量方法,该方法充分考虑了分类型数据的属性相关性、属性权重和有序特性,并将有序型属性和名义型属性进行了同质计算统一,从而保证了距离值的高区分度和高信息量。其次通过结合柯西核函数[20-21]重新评估密度值,改进了SNNDPC 算法中的数据密度计算和二次分配方式,使得算法不仅能够作用于分类型数据,还能有效缓解重叠和聚集问题,提高聚类性能。通过大量的对比实验和消融实验证明了CDPCD算法的有效性,CDPCD 也成为了当前鲜有的面向分类型数据的密度峰值聚类算法。
1 基于概率分布的加权有序距离度量
1.1 相关定义和特性统一
本节首先给出相关定义:设xij为数据集合X中数据点xi关于属性aj的属性值,其中1 ≤i≤n,1 ≤j≤m。设Ao为有序型属性集合,An为名义型属性集合,则Ao⋃An=A。为了方便后续公式说明,设O为数据的属性值集合,O={o1,o2,…,om},每个oj代表aj中数值的取值集合,oj={oj1,oj2,…,ojc(j)},其中C(j)表示该属性中可能取值个数,比如“性别”属性中共有“男”和“女”两个可能的属性取值,C(j)=2。
观察图3的分类型数据属性划分,从信息量层面可以认为有序型属性所提供的信息是同一内容的不同程度,而名义型属性则更侧重不同内容的信息,因此考虑属性的关联计算时难免会产生非同质的错误,为了避免这个问题,有必要将特性进行统一。有序型属性转变为名义型属性时会损失顺序信息,因此本文选择将名义型属性转换为有序型属性。转化方法的基本思想如图4所示,通过集合变换将名义型属性的每个可能取值转换为一个具有两个逻辑值的有序集合,两个逻辑值分别代表是否为当前可能取值的两种极端情况,例如“宠物”属性值中存在“猫”“狗”和“其他”三个取值,这三个取值被转换为三个“新”集合,“猫”“狗”“其他”,其中“猫”集合包含了两个极端值:是(用1 表示)、否(用0 表示),同理“狗”和“其他”也包含这两个极端值。通过集合变换,名义型属性所产生的属性集合可以被视为由多个有序型属性所组成,如上述“宠物”属性可视为由三个有序型属性组成的集合,于是可以将这个集合利用平均值等统计特征与原有的有序型属性进行计算。基于这种思想,有序型属性和名义型属性完成了同质计算统一,下节将利用这种方式辅助距离计算。

图3 分类型数据属性划分Fig.3 Categorical data attribute division

图4 名义特性变换Fig.4 Nominal feature transformation
1.2 距离度量方法
本节将提出一个全新且完整的分类型数据距离度量,包括属性关联、权重及有序特性所反映的顺序关系。其中属性关联利用条件概率分布[22]实现,属性加权使用信息熵[10,12],而顺序关系则考虑属性值之间转换的最小移动花费代价[23]。
在属性ar的属性值为orm条件下属性as的属性值为osp的条件概率如公式(1)所示:
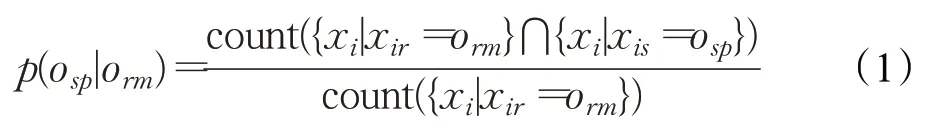
其中{xi|xir=orm}和{xi|xis=osp}分别代表了数据点xi的ar和as的属性值为orm和osp的数据集合,count()函数用于统计数据集合中数据的个数。通过公式(1),ar关于as所有属性值取值的条件概率分布可以用公式(2)所示的列表表示:

传统利用L1或L2范式的方法计算条件概率分布会容易损失顺序关系的信息,例如在计算U1=[1,0,0,0],U2=[0,1,0,0],U3=[0,0,0,1]三个分布的过程中,最终得到了‖U1-U2‖1=‖U1-U3‖1=‖U1-U2‖2=‖U1-U3‖2的结果,这与有序型属性的距离关系不符,显然第一与第二可能值之间应该比第一与第四可能值之间距离更近。本文使用了一种类似推土机算法[23]的计算方法保留了该关系,如公式(3)所示:


其中,在计算过程中使用均值完成特性的同质计算,与1.1 节对应,同时出于数据属性本身的特性要求,当ar∈Ao时再次考虑了顺序关系。
上述讨论假设数据属性的权重一致,但实际情况中由于不同属性值的分布不同,每个属性对距离的贡献是不同的,因此有必要对属性进行加权。信息熵是一种度量权重的方法,使用信息熵对属性进行加权能够很好地衡量随机变量的不确定度,尤其是离散型随机变量,因而适合分类型数据的离散分布特征[12]。信息熵的公式如式(6)、(7)所示:

容易验证公式(8)符合以下距离性质,是一种距离度量方法。

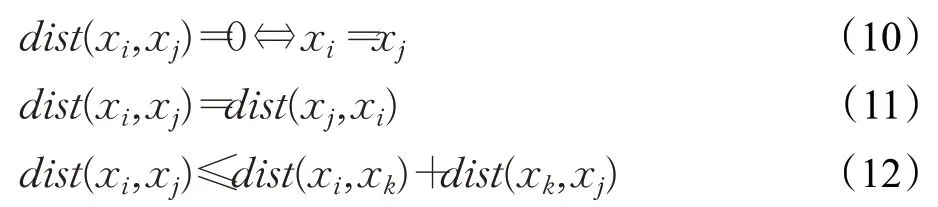
图5 展示了使用HDM、OF、Goodall 和本文提出的距离度量在Lenses数据集上的距离值集合,可以看到本文方法得到了更多的距离差异,保证了距离值的高区分度和高信息量,有效降低了重叠问题。
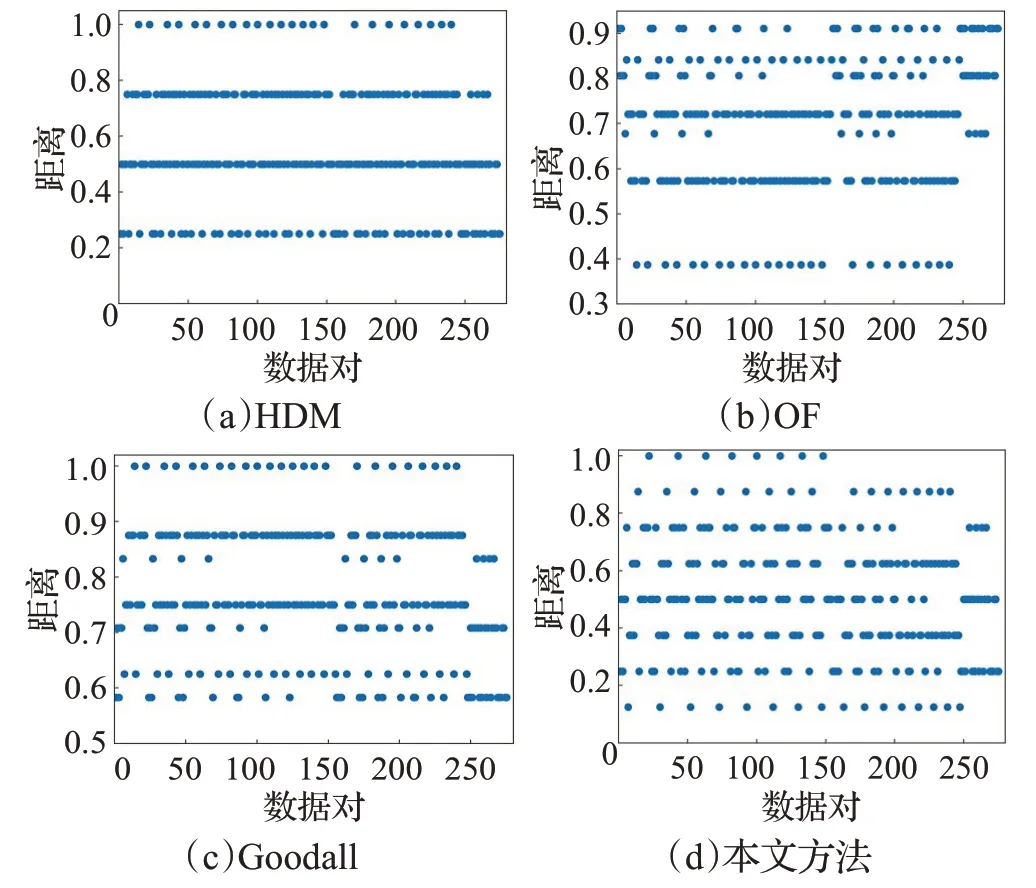
图5 距离度量结果Fig.5 Distance measurement results
2 结合柯西核函数的聚类算法
2.1 柯西核函数
尽管提出的距离度量增加了距离差异,但是分类型数据的密度计算仍然会产生聚集问题,需要一种考虑密度差异的评估方法。
核函数方法[21]能在密度计算的过程中考虑到更多数据对待评估数据的影响,比如常见的高斯核,但是高斯核的密度计算快速衰减特性使其容易忽视某些较远邻居的贡献。根据分类型数据相对分散的分布特点,这样的结果反而不利于区分密集区域的密度峰值点。相反如图6 所示,柯西核函数拥有更长的函数尾特征,因而空间中处于不同方向的密度峰值点会扩大考虑不同的较远数据的影响,从而更有利于数据密度计算结果的多样性。与此同时,柯西核函数的特性使其没有降低原先密集区域对密度计算的贡献,例如图7(a)、(b)所示经过排序后的Lenses数据集和Post数据集密度值图中,更平滑的蓝色点表示用柯西核计算出的密度值,而绿色点则使用了高斯核,可以看到绿色点区域中的密度值仍较为聚集,而蓝色点区分度较好,呈现出一个良好的上升趋势,有助于缓解聚集问题。

图6 高斯函数和柯西函数Fig.6 Gaussian function and Cauchy function
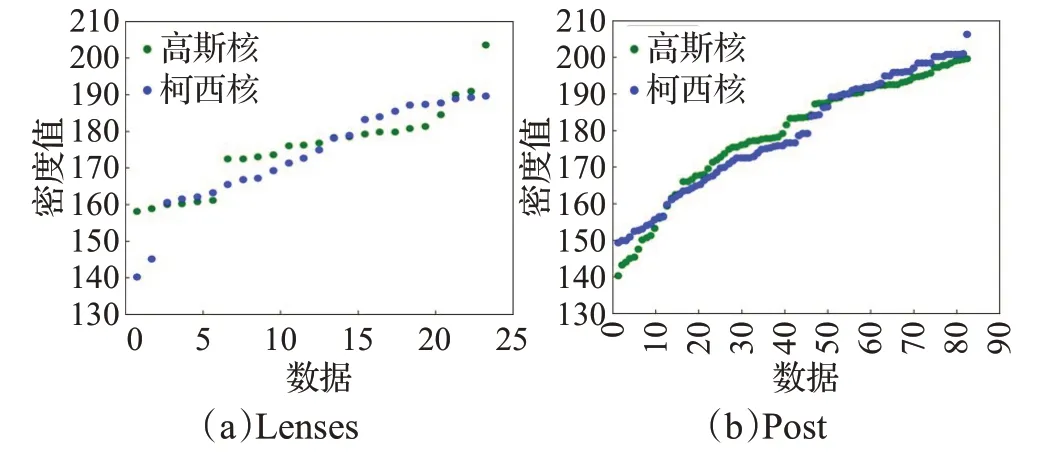
图7 数据集密度排序图Fig.7 Density sorting diagram of dataset
柯西核函数的另一个优势是运算方法简单,计算速度快。综上选择柯西核函数作为密度评估方法具有合理性和有效性。
两个数据结合柯西核函数的计算公式如式(13)所示,其中υi是关于n的超参数,本文使用xi与距离xi第K近的数据之间的距离作为υi。
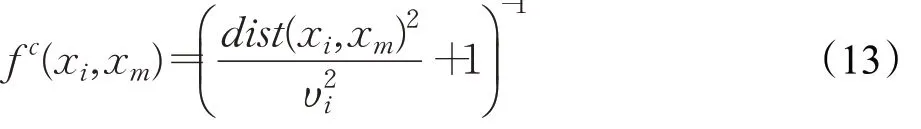
2.2 聚类算法
本节将介绍提出的CDPCD 算法,出于算法描述考虑,首先简要介绍原始算法(SNNDPC)的共享最近邻、相似度矩阵和二次分配方式[15]。
共享最近邻是指两个数据最近K个数据点中相同数据点的集合,记为SNN(xi,xj)=Γ(xi)⋂Γ(xj),其中Γ(xi)表示距离xi最近的K个数据点集合。
相似度矩阵是一个n维方阵,方阵中的值表示对应数据之间的局部相似度,计算过程如公式(14)所示:

二次分配方式将数据按照密度比例划分为不可避免从属点和可能从属点两类,并在划分过程中对数据进行相应的二轮分配,其中第一轮分配通过划分依据将不可避免从属点进行归类,第二轮分配则通过循环统计可能从属点最近邻中已分配数据的归属进行归类。
在密度计算上,CDPCD 定义的相似度矩阵在公式(14)的基础上结合了柯西核函数,基于的改进思想与2.1节对应,如公式(15)。同时关于计算数据xi密度峰值参数的和如公式(16)和公式(17)所示,其中在计算的过程中同样结合了柯西核函数。

在分配方式上,CDPCD 保留了从属点的命名及二次分配基本流程,但是划分依据和分配过程不同。其中划分依据方面,原始算法仅考虑数据之间共享一半数据点就划分为不可避免从属点,因此算法容易受到参数K的影响,过少或过多的K都会降低算法性能。此外分类型数据的数值分布在多数情况下会出现部分数据点集中但又与其他同类数据点分散的问题,如图8 所示,同一个类中出现了两个集中的数据组,甚至有些数据是重叠的(图中放大部分),因此重叠部分的数据点很可能由于共享最近邻重合导致无法被划分为不可避免从属点,最终产生两个后果,其一是在第二轮分配过程中被分配,从而产生一定的花费,其二是最终因为遗漏进而降低算法性能。CDPCD 考虑K与柯西核函数结合计算出的距离值并根据已分配数据点的最近邻平均距离值将数据进行划分,如定义1所示。这种划分依据会依靠数据本身最近邻点分布产生的均值作为阈值,这种阈值会保留相近点和重叠点,同时过滤远处的数据点,因而会尽可能将数据组合并,到达预期效果。与此同时CDPCD的划分依据会因为柯西核函数的加入而降低对K的敏感度,有利于算法的稳定。

图8 分类型数据存在的分布问题Fig.8 Distribution problems with categorical data

分配过程方面,原始算法在第二轮分配过程中会出现两个问题,即重复统计某一个已分配数据点和可能从属点出现多次统计最近邻数据点所属类却未被分配的情况,为了避免这两个问题,CDPCD在第二轮分配过程中通过考虑柯西核函数计算出的密度值影响,将可能从属点依照公式(13)计算出的距离值升序排序,并使用循环依次将可能从属点xi分配到Γ(xi)中距离最近的数据所在类中,在最近邻数据都未分配情况下将搜索空间变为整个数据集。这种分配过程使得每个可能从属点只计算一次就进行分配,从而能够有效解决重复统计却未被分配问题,加快第二轮的分配速度,同时基于出现就分配的原则,改进的分配方式也不会出现重复统计已分配数据点的情况。3.3.1 小节将通过实验证明分配过程在有效提速的同时并没有损失聚类效果的结论。
图9 给出了CDPCD 算法的流程示意图,其算法步骤如下所示:

图9 算法流程示意图Fig.9 Algorithm flow diagram
算法1 CDPCD
输入:数据集X,参数K。
输出:聚类结果R。
步骤1 根据公式(8)计算X中任意两个数据之间的距离。
步骤2 根据公式(16)与公式(17)计算数据的ρxi和δxi。
步骤3 通过决策图选取密度峰值点,对数据进行第一轮分配,根据定义1将不同密度峰值点的不可避免从属点归类。
步骤4 对标记的可能从属点进行第二轮分配,计算可能从属点结合柯西核函数的距离值,并升序排列;从队列中选取每个数据,按照最近邻原则分配,如果最近邻集合中数据均未分配,则分配到距离最近的当前已经分配的数据所在类中。
步骤5 记录数据分配结果,返回R。
算法1的时间复杂度主要在步骤1和步骤2上。步骤1中的距离度量主要取决C(j)的最大值,如果假设为q,则计算两个数据距离的时间复杂度为O(mq2),整个数据集的距离计算复杂度为O(mq2n2)。步骤2 中柯西核函数产生的计算为线性运算,故不存在多余运算代价,因此时间复杂度仅与K、m和n三个参数有关,为O((K+m)n2)。步骤3 和步骤4 的计算依赖步骤1 和步骤2,因此复杂度为O(1),故算法1 的总时间复杂度为O((mq2+K+m)n2)。与SNNDPC的O((K+m)n2)时间复杂度相比较,算法1中的mq2绝大部分情况下会远小于n2即属性值取值个数远小于数据量,因此算法1 和SNNDPC 的时间复杂度在数量级上是一致的,由于二次分配的优化,算法1在处理分类型数据集上会有额外增速优势。与K-modes 的O(E(kmn)) 时间复杂度和HDNDW 的O(E(kmqn+mn+mq2k))时间复杂度(注意这里的E为迭代次数,k为真实标签值)等划分聚类方法相比,算法1 不会受到随机结果影响,并且可以将距离计算和聚类过程分离,具有更好的灵活性。
3 实验部分
本文选用了表1 所示的15 组UCI 公开真实数据[11]作为进行各种实验的基本数据集,其中表1 的Attribute列定义为有序型属性列+名义型属性列。

表1 实验数据集Table 1 Experimental data sets
实验使用KM[3]、WKM[5]、MWKM[6]、EBDM-KM[10]、HDNDW[11]、UDMKM[12]与DPC[13]作为对比算法进行对比。按照文献及对比实验要求,KM、WKM、MWKM 和DPC使用HDM作为距离度量。此外,为了验证提出的距离度量以及柯西核函数方法在聚类上的有效性和重要性,在SNNDPC[15]和CDPCD 算法基础上增加了相应的消融实验。最后就CDPCD算法在划分依据和分配过程的时间提速方面进行了验证,并针对参数K对算法的影响和柯西函数相较于其他核函数的优势进行了实验。
本文参考的聚类评价指标[24-25]分别为标准化互信息NMI、调整兰德系数ARI 和福克斯马洛斯指数FMI,其中NMI 和FMI 的取值范围是[0,1],ARI 的取值范围是[-1,1],三个指标的数值越大,聚类的效果越好。
本文使用的编程环境为Matlab2021b 和Python3.6。算法的参数设置方面,KM、WKM、MWKM、EBDM-KM、UDMKM和HDNDW使用数据集的真实类别数目,由于这些方法具有随机性,因此会随机实验50 次取平均值作为最终结果;DPC算法的阈值参数设置为2%;其余算法存在最近邻参数K,本文选择重复实验并取NMI 最优结果值,K的最终设置范围在2~40。
3.1 对比实验
表2、表3和表4给出了各个算法在数据集上取得的聚类效果。

表2 NMI结果Table 2 NMI result

表3 ARI结果Table 3 ARI result

表4 FMI结果Table 4 FMI result
从表中可见在有序和名义特性都存在的数据集上(例如Lym、Flare等),进一步考虑有序特性的EBDM-KM、HDNDW 和UDMKM 算法比传统基于划分的MWKM、WKM 和KM 算法的聚类表现要好,这说明数据属性的进一步划分确实可以增加数据的信息量,提高聚类效果。CDPCD 算法不仅考虑了有序特性,而且统一了特性的同质计算,因此使其在Flare、Dermatology有序特征比例较高的数据集上比HDNDW、UDMKM等先进的分类型数据聚类算法更有竞争力。
在Soybean、Zoo等纯名义型属性的数据集上,CDPCD通过将名义特性转化为有序特性的手段,增加了距离信息量,缓解了距离度量的重叠问题,因而同样取得了较好的聚类结果。在纯有序型属性的数据集上,CDPCD通过密度值计算结果的多样性有效降低了聚集问题并减少了错误分配,从而更好地处理了基于划分算法不能有效捕捉复杂分布的问题,使得算法的性能更强。
与DPC 的对比结果中CDPCD 展示了其作为密度聚类算法却能够克服数据的距离值重叠问题和密度值聚集问题从而对分类型数据进行聚类的可能性和有效
性,CDPCD 通过新的距离度量和结合柯西核函数的方法让密度值的计算更符合分类型数据的需要,比如具有较高区分度的密度多样性等特征,这也为分类型数据的密度聚类方法提供了全新的解决思路。
3.2 消融实验
本节将通过消融实验进一步验证提出的基于概率分布的加权有序距离度量和结合柯西核函数方法计算密度值的重要性和有效性。实验使用SNNDPC和CDPCD作为两个基础算法,通过“控制变量”手段令SNNDPC 算法的距离度量使用本文提出的方法,并将方法记作CSNNDPC;CDPCD 算法的距离度量改为使用HDM、OF 和Goodall,分别记作CDPCD(HDM)、CDPCD(OF)和CDPCD(Goodall)。
表5给出了最终的聚类指标结果,其中每条数据集的指标结果的下一行Δ(%)表示CDPCD 与每个通过“控制变量”验证的算法在该数据集上对应指标的提高比,例如CDPCD 在Primary 数据集上相较于CSNNDPC的NMI 提高0.567 即56.7%。表5 的最后两行Avg 和AvgΔ(%)分别表示各个验证算法在所有数据集上的单一指标平均值和CDPCD相较于所有验证算法的单一指标在所有数据集上的平均提高比,例如CDPCD 在所有的数据集上相较于CSNNDPC的NMI平均提高0.642即64.2%。

表5 聚类结果Table 5 Clustering results
图10给出了三个聚类评价指标在各个验证算法和CDPCD算法上所有数据集上平均值的可视化结果。结果可见各个验证算法均没有达到CDPCD的平均聚类效果,CSNNDPC在缺少了柯西核函数增强密度多样性的效果后,其聚类效果明显降低。正如2.1节所述,柯西核函数提供的平滑、有差别的密度值计算结果能够很好地区分不同数据对所属类的贡献差别。此外这种密度多样性的特征不仅仅体现在解决密度计算聚集问题的柯西核函数上,由于密度计算依赖距离度量,三个控制距离度量方法的算法得到的聚类结果较差,说明了提出的距离度量方法在后续计算数据密度值和进行聚类的过程中起到了关键作用,尤其在纯有序型的数据集上NMI和ARI的结果平均下降非常大,证明缺少了有序特性的距离度量方法后,聚类算法会在运行过程中损失许多有用的顺序信息,导致性能变差。

图10 验证算法和CDPCD在数据集上的平均聚类效果Fig.10 Average clustering effect of validation algorithm and CDPCD on dataset
3.3 其他实验
3.3.1 时间对比实验
本小节将对2.2节中算法1的分配过程加速且不损失算法性能的结论进行实验验证,为了更好对比实验结果,选择Wisconsin、Tic、Lecturer、Social 和Car 五个较大的数据集进行实验,并将两个算法的参数K设置为相同值,最后统计聚类指标NMI和运行时间Time。表6给出了最终的结果,其中每个数据集分别对原始算法(Mode 列标为original)和改进的算法(Mode 列标为now)进行实验。从表中可见,相较于原始算法,CDPDC在基本不损失聚类性能的前提下均有一定的提速,说明该分配方式更加符合分类型数据的特点,能够提高运行速度,同时在大多数数据集上NMI 指标得到了提高也侧面说明了算法改进能够提高一定的聚类性能。

表6 运行时间实验结果Table 6 Running time experiment results
3.3.2 参数实验
CDPCD算法的执行需要参数K,本小节通过简要举例分析该参数对聚类结果的影响。
如图11,在Zoo 和Dermatology 数据集上设置参数K的范围为[5,40]并运行算法统计其NMI,可以发现指标随着K的增加而上升,并逐步达到最大值,随后下降。同时在最大值参数K附近的指标差值较小,说明该参数还具有一定的鲁棒性。
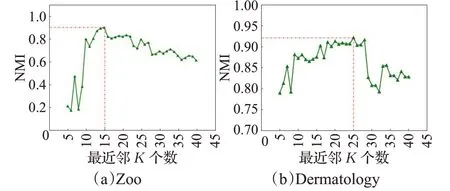
图11 参数K 对聚类结果NMI的影响Fig.11 Effect of parameter K on clustering result NMI
3.3.3 核函数实验
本小节对柯西核函数的有效性进行验证,实验选取有序型+名义型、纯有序型和纯名义型的若干数据集并使用目前常见考虑数据之间距离的高斯核(GK)、二次有理核(RQK)和幂指数核(EK)进行比较。表7给出了最终结果,其中表中的最后列为柯西核(CK),可以看到由于缺乏重尾核函数提供的平滑密度值过渡特性,这些对比核函数不能够为分类型数据提供符合其数值分布的良好空间特点,因此聚类性能较差。

表7 核函数对比实验结果Table 7 Kernel function comparison experimental results
4 结束语
本文提出了结合柯西核的分类型数据密度峰值聚类算法。算法首先针对密度聚类中距离计算产生的重叠问题,提出了一种全新的基于概率分布的加权有序距离度量来增强距离计算的高区分度和高信息量。然后针对密度计算产生的聚集问题,使用了一种结合柯西核函数的密度估计方法重新计算数据局部密度值,同时改进了SNNDPC 算法的划分依据和二次分配过程。实验证明本算法显著提高了分类型数据的聚类效果,但是本算法在处理高维分类型数据集下存在计算量较大的问题,如何有效降低计算消耗将是下一步研究的重点方向。
