面向整体区域的改进VIRE定位算法研究*

牛 琨，高仲合，张 凡

(曲阜师范大学网络空间安全学院,山东 曲阜 273165)

1 引言

伴随着普适计算(Ubiquitous Computing)的正式提出，人们可以通过各种信息传感设备实时采集、监督和管理目标的数据信息[1]。其中，位置信息服务的研究逐渐成为热点。在室外定位方面，基于卫星的定位系统凭借大范围、高精度等优势已广泛应用于军事侦察、气象监测和运输监管等领域[2]；在室内定位方面，研究机构根据复杂的信道环境及现有成熟的无线通信技术提出了多种定位系统[3-7]，无线射频识别RFID(Radio Frequency IDentification)凭借非接触、非视距、高精度和低成本等特点成为优选的室内定位技术之一[6]，已广泛应用于护理监测、车间管理等领域[8 - 10]。

近年来，基于接收信号强度指示RSSI(Received Signal Strength Indication)的测距定位机制成为了最常用的RFID定位机制[11]，该机制依靠路径损耗模型将接收到的信号强度值转化成距离信息后进一步求解。LANDMARC(LocAtioN iDentification based on dymaMic Active RFID Calibration)定位算法就是其中的典型应用。VIRE(VIrtural Reference Elimination)算法在LANDMARC算法的基础上引入虚拟参考标签，利用线性插值计算虚拟参考标签的RSSI值，通过邻近地图去除冗余位置信息。其优点是在不增加额外成本和信号干扰的同时，提高定位标签的定位精度。但是，VIRE算法的虚拟参考标签全部设置在中心区域的参考标签矩形阵列中，导致边缘区域定位精度低，并且虚拟参考标签RSSI值计算所采用的线性插值也不符合实际情况；其次，选取邻近参考标签时所采用的固定阈值可能出现邻近参考标签“唯一性”；同时，在实际情况中需要根据室内环境反复地手动调整阈值才能达到最佳效果；最后，由于多径效应引起的参考标签RSSI值与预期相差过大的情况偶有发生，这些都会影响到虚拟参考标签的RSSI值与定位标签的定位精度。

针对上述VIRE算法的不足，本文提出一种面向整体区域的VIRE定位算法。首先，增加虚拟参考标签数量，扩大虚拟参考标签分布，并且运用牛顿插值方法计算虚拟参考标签的RSSI值，提高整体定位区域定位标签的定位精度；其次，采用动态阈值的方式避免邻近参考标签的“唯一性”，提高定位系统对复杂环境的适应性；之后，通过计算所有邻近参考标签之间的距离来判断邻近参考标签是否出现RSSI值与预期相差过大所导致的不可信情况；最后，运用误差校正方法计算定位标签的最终位置坐标。

2 VIRE算法

为了解决LANDMARC算法定位精度与参考标签数量之间的冲突问题[12,13]，VIRE算法在参考标签的基础上引入了虚拟参考标签。算法将4个相邻的参考标签所围成的矩形区域称为物理网格单元，每个物理网格单元被划分为N*N个虚拟网格单元，虚拟网格单元的顶点位置插入虚拟参考标签，通过线性插值求得RSSI值。虚拟参考标签水平方向和垂直方向的RSSI值计算分别如式(1)和式(2)所示：

(1)

(2)

其中，Rl(Ti,j)表示第l(1≤l≤L)个读写器读取/计算得到的位于(i,j)坐标的参考标签/虚拟参考标签的RSSI值，L表示读写器的总数量，a=i/n，b=j/n,p=imodn(0≤p≤n-1),q=jmodn(0≤q≤n-1)。

将第l个读写器读取的定位标签RSSI值与虚拟参考标签RSSI值作差，若差值在固定阈值以下则标记为1，反之为0，由此得到第l个读写器对于定位标签的差值矩阵，称为“邻近地图”。所有读写器重复此操作得到邻近地图后，取所有邻近地图的交集(即只取相同位置元素值为1的参考标签)得到最终的邻近地图。选择邻近地图中元素值为1的参考标签作为该定位标签的邻近参考标签，代入如式(3)所示的权重因子计算公式可得最终位置坐标。

(3)

权重因子W1i中Rl(Ti)是第l个读写器接收到第i个邻近参考标签的RSSI值，Rl(θ)是第l个读写器接收到的定位标签的RSSI值。因此，权重因子W1i与邻近参考标签和定位标签之间的RSSI差值有关，W1i越小,表示邻近参考标签拥有越高的参考性。

将邻近地图中互相连接的邻近参考标签记为群，权重因子W2i的计算如式(4)所示：

(4)

其中，na表示群数，nci表示第i群中的邻近参考标签的数量。因此，权重因子W2i与邻近参考标签的群体密度有关，W2i越大，表示该群中的邻近参考标签拥有越高的参考性。

VIRE算法采用Wi=W1i*W2i作为综合权重因子计算定位标签的最终坐标位置，如式(5)所示：

(5)

3 改进VIRE定位算法

3.1 定位区域虚拟参考标签分布方案

假设实验场景如图1所示，在8 m*8 m的定位区域放置4台读写器，在中心区域规则地放置16个间隔为2 m的参考标签。VIRE算法在每4个相邻的参考标签所围成的区域内插入(N+1)2-4个虚拟参考标签(见图1中心区域)。通过分析可知，当定位标签落入中心区域时，定位标签与所选择的邻近参考标签之间坐标位置接近，且邻近参考标签具有较好的参考性；当定位标签落入边缘区域时，定位标签与所选择的邻近参考标签之间距离较远，甚至难以选择合适的邻近参考标签，此时邻近参考标签的参考性大大降低。为了解决定位区域参考标签分布不均衡，边缘区域的定位标签定位精度低的问题，本文在VIRE算法参考标签分布的基础上，在边缘区域中插入虚拟参考标签。

Figure 1 Reference label distribution map of the VIRE algorithm in overall region图1 VIRE算法整体区域参考标签分布图

VIRE算法的整体区域虚拟参考标签分布图如图1所示。在边缘区域的每个1 m*2 m的矩形中插入(N+1)2-2个虚拟参考标签，使定位区域的虚拟参考标签分布更加均衡，提高边缘区域定位标签的定位精度。4个角的1 m*1 m区域不设置虚拟参考标签的原因将在3.2节说明。

3.2 基于牛顿插值的标签RSSI值计算

由于信号的衰减程度是复杂的非线性关系，所以在VIRE算法中利用线性插值计算虚拟参考标签RSSI值容易带来额外的误差。文献[14]利用牛顿插值对虚拟参考标签的RSSI值进行了估算；文献[15]通过克里金插值计算虚拟参考标签的RSSI值。 本文在多种内插法中选择具备良好的扩展性和适应性的牛顿插值代替线性插值。牛顿插值法如下所示：

设多项式函数f(x)，(x0,f(x0)), (x1,f(x1)), (x2,f(x2)),…,(xn,f(xn))是n+1个相对于多项式f(x)的互不相等的点。式(6)表示f(x)关于点x0,x1,…,xn的n阶差商:

f[x0,x1,…,xn]=

(6)

将n阶差商代入插值多项式，最终得到式(7)所示的牛顿插值多项式：

f(x)=f(x0)+f[x0,x1](x-x0)+…+

f[x0,x1,…,xn](x-x0)(x-x1)…

(x-xn-1)+f[x0,x1,…,xn](x-x0)

(x-x1)…(x-xn-1)(x-xn)

(7)

因此，当出现增加节点的情况时，牛顿插值法能够在不改变多项式前项的前提下根据增加的节点数量扩充多项式后项，具有良好的扩展性和适应性。利用牛顿插值法计算虚拟参考标签的RSSI值的步骤如下所示：

(1)将参考标签按照与读写器的距离升序排列组成行向量，对行向量做“唯一”操作去除重复距离元素后得到向量D作为插值自变量，之后将向量D中的距离元素对应的RSSI值组成向量R作为插值因变量。

(2)为了避免高次牛顿插值多项式引起的龙格现象，将插值变量进行分段：设向量D的元素数量为m，按照(1,m/3),(m/3,2m/3),(2m/3,m)将向量D分成元素数量相同或相近的3组，将对应序号的距离元素分别代入向量D1,D2和D3，向量R中的对应元素也代入向量R1,R2和R3。

(3)将虚拟参考标签按照与读写器的距离依次代入对应分组的牛顿插值多项式计算RSSI值。

通过上述分段方法能够使各段插值多项式包含相同或相近的节点个数，以此平衡各段插值多项式的计算能力；同时，各段插值多项式的已知节点位于端点两侧，可以有效实现数值内插，提高牛顿插值法的准确性。由此可知，如果在定位区域4个角的1 m*1 m区域设置虚拟参考标签,则超出了分段牛顿内插法的范围，导致虚拟参考标签的RSSI值不准确，影响边角区域定位标签的定位精度，因此，定位范围4个角的1 m*1 m区域不设置虚拟参考标签。

3.3 动态阈值调整方案

阈值是VIRE算法选择邻近参考标签的重要参数，也是影响算法定位准确度的重要因素。VIRE算法采用固定阈值机制，虚拟参考标签的密度决定阈值的最佳选择：当虚拟参考标签密度较大时，距离定位标签较远的低参考性标签可能混入邻近参考标签，导致标签的定位误差增大；反之，当虚拟参考标签密度较小时，邻近参考标签数量少甚至无法选出邻近参考标签，则会导致边缘区域定位标签的定位误差大，甚至无法对定位标签进行定位；同时，在实际实验中，由于实验环境复杂多变，需要反复手动调整阈值，以达到最佳定位效果，这增加了实验难度。文献[15]采用自适应阈值调整策略，通过调整将邻近参考标签数量维持在0.3*Nmax～Nmax(Nmax=LV/M，L是读写器总数，V是虚拟参考标签总数，M是参考标签总数)，系统性能得到了有效提升。因此，本文将采用动态阈值机制解决上述问题，初始阈值TH设置为1，阈值调整值设置为0.05。

动态阈值机制具体流程如下所示：

(1)设置初始阈值TH=1，遍历全图参考标签，若参考标签的RSSI值与定位标签的RSSI值的差值在阈值以内，则标记为邻近参考标签。

(2)统计邻近参考标签数量Q，若Q小于邻近参考标签数量下限值Qmin，则增大阈值，重复选择过程，直至其数量在范围以内；若Q大于邻近参考标签数量上限值Qmax，则减小阈值重复操作(邻近参考标签上下限值Qmin和Qmax将在4.3节具体说明)。

(3)通过动态阈值机制得到所有定位标签的邻近参考标签后，接下来进入权值计算环节。

3.4 邻近参考标签可信度与误差校正方案

在实际测试中，由于室内环境复杂多变，参考标签距离过近等因素，容易引发多径效应，导致信号的衰落和相移，进而影响参考标签的RSSI值，使其与距离值不匹配[16]。这就是提出的邻近参考标签的可信问题。

邻近参考标签是满足阈值条件，且与定位标签的RSSI值最接近的参考标签，通过RSSI值与距离的转化计算，邻近参考标签也是距离定位标签最近的参考标签。但是，如果邻近参考标签中包含的RSSI值出现较大偏差的参考标签时，出现偏差的邻近参考标签距离其他邻近参考标签的距离过远，按照原方案代入权值计算位置坐标后，定位标签的定位效果会受到影响。因此，对于距离其他邻近参考标签过远的邻近参考标签来说，需要设置可信距离阈值来判断此邻近参考标签是否可信。邻近参考标签可信度检查过程如下：

首先，计算定位标签的所有邻近参考标签间的距离，并将其组成如式(8)所示的距离矩阵：

(8)

然后，每个定位标签根据邻近参考标签的数量组成对应维数的矩阵。其中，dij表示第i个邻近参考标签到第j个邻近参考标签之间的距离，对距离矩阵做行向量绝对值运算，求出每个邻近参考标签距离其他邻近参考标签的平均距离，如式(9)所示：

(9)

在VIRE算法中，中心区域的定位标签都位于虚拟网格单元内，若定位标签确定的邻近参考标签数量Q≤4，那么虚拟网格单元顶点的4个虚拟参考标签具有最高的参考性；若该定位标签确定的邻近参考标签数量Q≤16，那么虚拟网格单元外围的12个虚拟参考标签同样具有较高的参考性，以此类推。通过推理可得，可信距离阈值与虚拟参考标签的密度N和邻近参考标签数量Q有关，当虚拟参考标签密度越大时，所有邻近参考标签的坐标就越集中，可信距离阈值应当降低；当邻近参考标签数量越多时，邻近参考标签之间的距离就越远，可信距离阈值应当提高。本文以间隔为2 m的参考标签为基础，利用高参考性的邻近参考标签所围成的矩形区域边长作为可信距离阈值dmax，得出式(10)：

(10)

其中，Qoutput的取值与邻近参考标签数量Q的范围有关，如表1所示。

Table 1 Relation table of the number of adjacent reference label number Q and Qoutput

若邻近参考标签的平均距离全部位于可信距离阈值以下，则认为邻近参考标签全部可信；若有不超过对应Qoutput取值的邻近参考标签的平均距离大于可信距离阈值，则保留剩余可信邻近参考标签；若有超过对应Qoutput取值的邻近参考标签的平均距离大于可信距离阈值，证明当前实验环境不理想，需要重新布置实验环境后再次实验。

确定最终邻近参考标签后，采用邻近参考标签误差校正策略进一步减小定位误差[13]。具体流程如下：

(1)对于定位标签的Q个邻近参考标签，分别将其看作是“暂时定位标签”，其余的Q-1个邻近参考标签看作是参考标签，通过3.1～3.3的改进机制得到Q个暂时定位标签的邻近参考标签。

(2)利用式(3)～式(5)计算得出暂时定位标签的位置坐标(x′i,y′i) (i=1,2,…,Q)，将其与实际坐标(xi,yi)比较，得到暂时定位标签的位置误差，如式(11)所示：

(△xi,△yi)=(xi-x′i,,yi-y′i)

(11)

(3)整合所有暂时定位标签的位置误差得到该定位标签的校正值，如式(12)所示：

(12)

(4)利用校正值对该定位标签的估计坐标进行校正，得到最终定位坐标，如式(13)所示：

(x*,y*)=(x,y)+(△x,△y)

(13)

4 改进算法的仿真实验结果对比

本文通过Matlab进行仿真实验，采用对数路径损耗模型，取路径损耗指数nn=2[17]，虚拟参考标签密度N=10，动态阈值初始值TH=1。定位布局如图2所示，在定位区域的不同位置随机生成30个定位标签，包括：位于中心区域的1～10号标签，边缘区域的11～20号标签和边角区域的21～30号标签。本文将重复进行100次实验得出的待测标签的定位坐标平均值作为最终定位坐标。

4.1 不同虚拟参考标签分布实验

为测试3.1节提出的定位区域虚拟参考标签分布方案，本文设计不同虚拟参考标签分布的定位实验：将定位标签分别布署在VIRE算法的虚拟参考标签分布图与面向整体区域的虚拟参考标签分布图中，记录不同虚拟参考标签分布的定位误差，实验结果如图3所示。

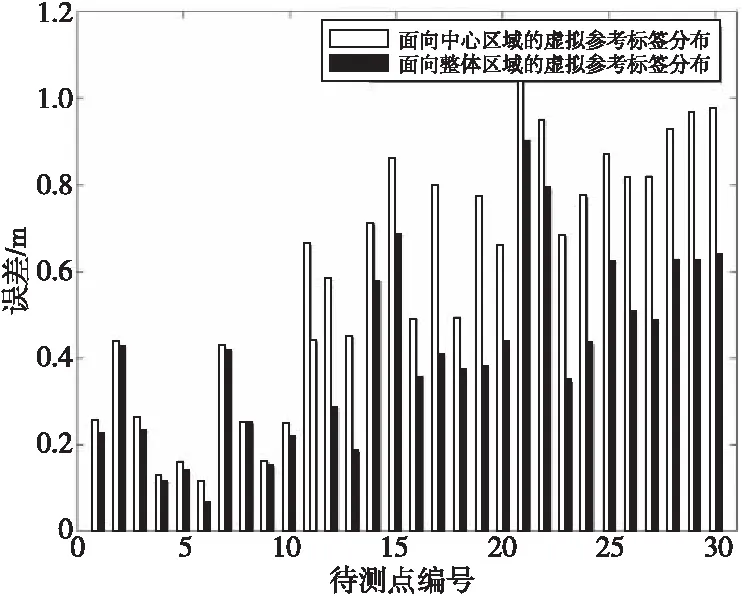
Figure 3 Experimental results on distribution of different virtual reference labels图3 不同虚拟参考标签分布实验结果

由图3可以看出，面向整体区域的虚拟参考标签分布中的定位误差更小，在边缘和边角区域尤其明显。其中，面向中心区域的虚拟参考标签分布中的平均误差为0.589 7 m,最大误差为1.047 0 m，最小误差为0.110 7 m；面向整体区域的虚拟参考标签分布中的平均误差为0.409 9 m，最大误差为0.902 2 m，最小误差为0.063 7 m。

4.2 不同插值方法的RSSI值计算实验

为测试3.2节提出的基于牛顿插值的虚拟参考标签RSSI值计算方法，本文在4.1节的基础上设计不同插值方法的定位算法实验：将定位标签分别输入基于线性插值的定位算法和基于分段牛顿插值的定位算法中，记录不同插值类型的定位误差，实验结果如图4所示。

Figure 4 Experimental results of positioning algorithms with different interpolation types图4 不同插值类型的定位算法实验结果

由图4可以看出，基于分段牛顿插值的定位算法相较于前者的定位误差有明显下降。基于分段牛顿插值的定位算法中的平均误差为0.278 2 m，最大误差为0.827 7 m，最小误差为0.024 5 m。

4.3 动态阈值调整方案实验

3.3节中提到，利用阈值的动态调整与邻近参考标签数量上、下限值Qmin、Qmax的限制，可以使邻近参考标签数量Q始终保持在最佳范围内。之后，通过4.2节的定位算法实验发现，所有定位标签的邻近参考标签数量在12～36，为了确定基于动态阈值的定位算法中邻近参考标签的最佳上、下限值，本文通过调整算法中邻近参考标签的下限值和上限值来进行邻近参考标签数量选择的实验，实验结果如图5所示。

Figure 5 Upper and lower limits on the number of adjacent reference labels图5 邻近参考标签数量上下限实验结果

从图5中可以看出，当邻近参考标签下限值在1～20增长时，定位算法的误差出现小幅下降，当下限值从20开始增长时，误差有明显的增大趋势；当邻近参考标签下限值确定时，上限值距离下限值过近或过远都会导致误差增大，所以，适中的上、下限值距离同样重要。其中，35～40有0.189 5 m的最大误差，10～25有0.126 2 m的最小误差，所以基于动态阈值的定位算法中取10为下限，25为上限。

为测试3.3节提出的动态阈值调整方案，在4.2节的基础上，设计不同阈值类型的定位算法实验：将定位标签分别输入基于固定阈值的定位算法和基于动态阈值的定位算法中，记录不同阈值类型的定位误差，实验结果如图6所示。

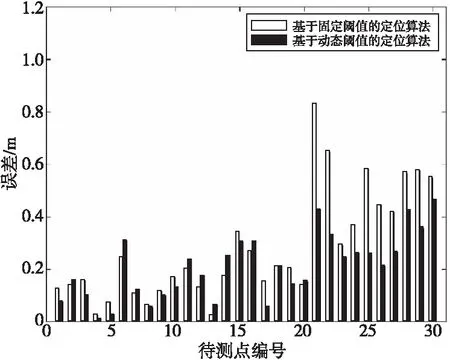
Figure 6 Experimental results of location algorithm with different threshold types图6 不同阈值类型的定位算法实验结果

从图6可以看出，在中心和边缘区域，基于动态阈值的定位算法相较于前者的定位误差存在持平或小幅降低；在边角区域，基于动态阈值的定位算法的定位误差则显著降低。基于动态阈值的定位算法中的平均误差为0.207 9 m，最大误差为0.466 0 m，最小误差为0.007 5 m。

4.4 邻近参考标签误差校正方案实验

为了测试3.4节提出的邻近参考标签误差校正方案，本文设计运用邻近参考标签误差校正方案的定位实验。在定位区域内，由于边角区域附近的虚拟参考标签所处的位置属于牛顿外部插值范围，RSSI值有所偏差，为了防止边角区域的定位标签误差增大，位于边角区域的定位标签不采用邻近参考标签偏差校正策略。之后，将定位标签分别输入不采用邻近参考标签误差校正的定位算法和采用邻近参考标签误差校正的定位算法中，记录对应的定位误差，实验结果如图7所示。

Figure 7 Experimental results of with/without adjacent reference labels error correction location algorithm图7 采用/不采用邻近参考标签误差校正的定位算法实验结果

从图7中可以得出，在采用邻近参考标签误差校正策略的中心和边缘区域中，大多数标签的定位误差都有不同程度的降低。该定位算法中定位标签的平均误差为0.153 2 m，最大误差为0.466 0 m，最小误差为0.005 8 m。

4.5 改进算法性能实验

以VIRE算法为基础，上述实验中采用的定位区域虚拟参考标签分布方案、分段牛顿插值方案、动态阈值调整方案和邻近参考标签误差校正方案的定位误差统计结果如表2所示。

Table 2 Location error for various strategies

通过表2可知，采用的4种方案均能提升算法的定位精度。整合以上4种方案组成面向整体区域的改进VIRE定位算法。VIRE算法与改进VIRE算法的定位误差对比如图8所示。

Figure 8 Comparison of location error between VIRE algorithm and the improved VIRE algorithm图8 VIRE算法与改进VIRE算法的定位误差对比

从图8中可以看出，改进VIRE算法定位误差大幅降低，VIRE算法的中心区域、边缘区域和边角区域的平均误差分别为0.242 3 m,0.646 2 m和0.880 6 m，改进VIRE算法的中心区域、边缘区域和边角区域的平均误差分别为0.044 4 m,0.089 9 m和0.325 3 m。因此，改进VIRE算法呈现出了较好的定位性能。

为了进一步研究不同定位区域的定位精度，下面以点(4,4)为圆心、4为半径的圆内区域设为中央区域，在定位区域内投入5 000个定位标签，其中中央区域内的定位标签占比为0.8，对比VIRE算法与面向整体区域的改进VIRE算法的累积分布函数CDF(Cumulative Distribution Function)曲线,如图9所示。

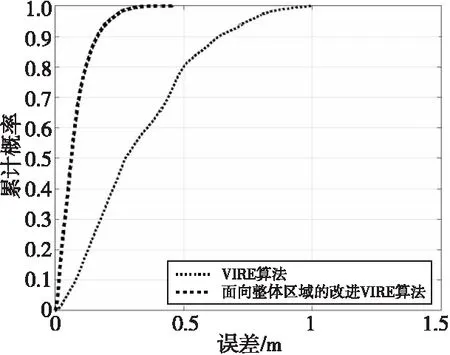
Figure 9 CDF curve comparison of VIRE algorithm and thd improved VIRE algorithm图9 VIRE算法与改进VIRE算法的CDF曲线对比图

由图9可知，VIRE算法的定位误差以50%的概率低于0.284 8 m，以80%的概率低于0.496 0 m，最大误差为0.992 8 m；面向整体区域的改进VIRE算法的定位误差以50%的概率低于0.065 6 m，以80%的概率低于0.122 8 m，最大误差为0.391 5 m。因此，面向整体区域的改进VIRE算法具有更好的定位效果。

5 结束语

本文针对VIRE算法环境适应能力有限、边缘区域定位精度低等问题，提出了面向整体区域的改进VIRE定位算法。通过Matlab仿真实验验证了改进算法采用整体区域虚拟参考标签分布方案、分段牛顿插值方案、动态阈值调整方案、邻近参考标签可信度与误差校正方案后，算法的中心区域、边缘区域和边角区域的平均误差分别为0.044 4 m,0.089 9 m和0.325 3 m，在整体定位区域内体现出较好的定位精度与较强的环境适应能力。该算法可以有效应用于RFID室内定位领域，例如物流管理、生产制造等，因此具有较高的应用价值。