基于压缩感知和DNA编码的图像加密算法*

邓文博,刘 帅,刘福才,黄茹楠

(燕山大学工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)

1 引言

随着互联网的普及，人们会通过网络传输各种数据，信息泄露的风险也随之增大。图像加密是为多媒体数据提供安全保障的技术之一。由于混沌系统对初值敏感[1]，而且混沌序列是伪随机的，非常适合用于图像加密。Cavusoglu等[2]提出了基于混沌S盒的图像加密方案;Slimane等[3]将Logistic映射和Chua电路相结合定义复杂映射，生成用于加密的混沌序列;张海英等[4]采用分数阶混沌进行图像加密。这些加密方案只是从信息安全的角度设计的，没有考虑图像本身的特性。

图像的高冗余度和相邻像素的强相关性，导致其传输效率不高。合理压缩加密图像，既能提高传输速度又不影响图像质量，因此对图像压缩加密的研究具有重要意义。王厚林等[5]提出压缩感知CS(Compressed Sensing)与混沌系统比特级的加密算法。该算法不仅加密效果优良，而且还可以抵抗由统计攻击和差分攻击组成的穷举攻击等多种破坏行为，但在抵抗噪声攻击方面并不理想。Chai等[6]提出了一种基于四维混沌系统和元胞自动机的压缩感知图像加密算法。Ponuma等[7]将一种新的一维混沌映射用于压缩感知图像加密，该算法尽管加密效果良好，但其使用的是低维混沌系统，存在安全性不足的问题，且抗噪声、抗裁剪能力弱。

由于DNA高度并行，越来越多基于DNA编码的图像加密方案应运而生。谭琳等[8]提出了基于DNA序列和混沌的图像加密算法。涂正武等[9]提出了基于DNA序列的彩色图像加密算法。然而，基于DNA和混沌系统的加密算法不能抵抗选择明文攻击。

传统单一的图像加密算法在安全方面仍有很大的改进空间。为了克服以上方案存在的不足，本文提出一种将压缩感知与DNA编码相结合的图像加密算法。首先，在图像加密前通过CS对图像进行预处理且CS的测量矩阵由克罗内克积KP(Kronecker Product)构造；然后，通过对压缩图像进行DNA编码加密，降低了图像相邻像素的相关性，提升了加密图像抗噪声、抗裁剪性能。超混沌序列动态控制DNA编码,增加了加密过程的复杂度。使用原始图像的256位哈希值生成混沌系统的初始值，能够抵抗选择明文攻击。仿真实验结果表明,本文算法加密效果良好、传输效率快、抗攻击能力强。

2 算法基础

本节主要介绍混沌系统、DNA编码技术、克罗内克积和压缩感知技术。

2.1 混沌系统

混沌系统主要由Logistic混沌和超混沌Bao系统组成。

(1) Logistic混沌。

Logistic混沌是一种经典的一维混沌映射，起源于虫口模型。具体数学表达如式(1)所示：

wn=uwn-1(1-wn-1)

(1)

其中,u为分支参数，{wn}为得到的混沌序列。当u∈(3.5699,4],wn∈[0,1]时，系统处于混沌状态。

(2)超混沌Bao系统。

通过对三维混沌Bao系统进行改进，构建四维超混沌Bao系统[10]，其数学模型如式(2)所示：

(2)

其中，e是控制参数;x,y,z,h是状态变量;a,b,c是常数。当a=20,b=4,c=32,e≥0时，称系统为超混沌Bao系统。

2.2 压缩感知技术

压缩感知，是一种信号采样技术，可在采样过程中同时完成数据压缩。

图像本身是一种二维或三维信号，本文算法处理的是二维灰度图像。假设原始图像I的大小为N×N，若I可以被稀疏表示,则：

CS_I=Φ1IΦ2T

(3)

其中,Φ1和Φ2为测量矩阵，大小为M×N，对应亚采样过程，测量矩阵将高维信号I投影到低维空间；CS_I为测量值图像，大小为M×N，也就是亚采样后的结果。本文算法中测量矩阵由随机高斯矩阵构成。

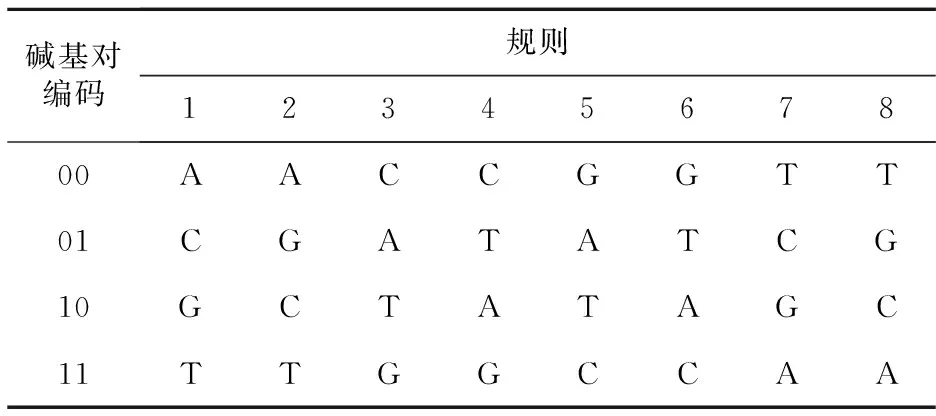
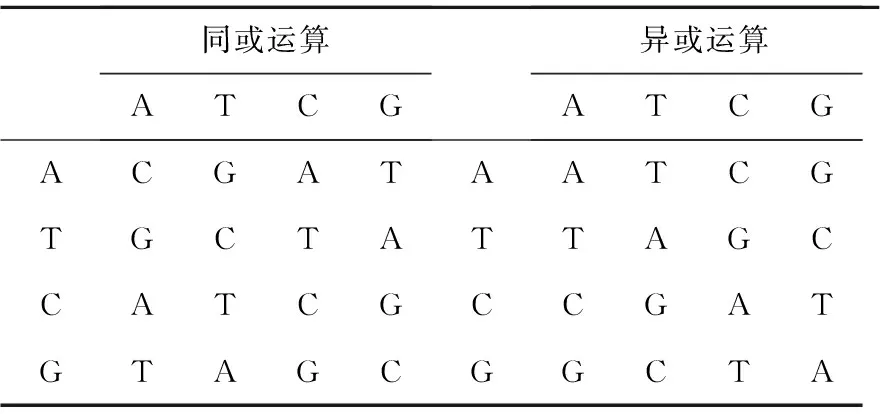
式(3)中，由于M

(1)原始图像I是稀疏的。在某种稀疏基上对原始图像I进行稀疏表示。常用于稀疏分解的基有傅里叶变换基、小波变换基和离散余弦变换基等。本文采用小波变换基对图像信号进行稀疏表示，如式(4)所示：

S=ΨIΨT

(4)

其中,Ψ为稀疏基矩阵，大小为N×N;S为稀疏系数矩阵，大小为N×N。

(2)Φ1和Φ2需满足有限等距性质RIP(Restricted Isometry Property)，但判断测量矩阵是否具有RIP性质是非常困难的。相关研究表明，RIP的等价条件是测量矩阵Φ1、Φ2与稀疏基Ψ不相关，因此可将稀疏图像S转化为最小化问题进行求解，如式(5)所示：

min‖S‖0subject toCS_I=Φ1SΦ2T

(5)

其中,‖S‖0为稀疏系数矩阵S中非零向量的个数。

信号的重构就是采用某些算法，利用低维测量信号恢复出高维原始信号的过程。选择的测量矩阵和重构算法将直接影响重构信号的质量。本文采用的测量矩阵为随机高斯矩阵，重构算法为正交匹配追踪OMP(Orthogonal Matching Pursuit)算法。

2.3 克罗内克积

克罗内克积是张量积的一种特殊形式，它表示任意2个大小的矩阵之间的运算关系。若A为m×n的矩阵，B为p×q的矩阵，则A⊗B是一个mp×nq的分块矩阵,如式(6)所示:

(6)

若A和B是线性无关的正交矩阵，根据KP的性质，可通过低维的线性无关正交矩阵得到高维的线性无关正交矩阵。本文利用该方法构造CS测量矩阵。

2.4 DNA编码技术

在生物基因学中，每一条DNA包含4种碱基对，分别为A、T、C和G。其中，A与T互补配对，C与G互补配对。若用二进制表示4种碱基对，则满足互补配对原则的规则共有8种，如表1所示。

Table 1 Rules of DNA encoding and decoding

根据表1的规则,假设像素值为114，二进制表示为01110010，将其按规则2进行DNA编码得到GTAC，再按规则6解码得到二进制数00011011，转换为十进制即为27。通过一次简单的DNA编码和解码，即可使一个像素值发生极大改变,这是基于DNA编码加密图像的基本原理。在此基础上再进行DNA序列之间的运算，则可得到更好的图像加密效果。本文采用的加、减法运算规则如表2所示，异或、同或运算规则如表3所示。

Table 2 DNA addition and subtraction operations

Table 3 DNA XOR and XNOR operations

3 加密和解密流程

图像压缩加密解密算法过程如图1和图2所示。

Figure 1 Process of encryption图1 加密过程

Figure 2 Process of decryption图2 解密过程

假设原始图像I的大小为N×N，图像压缩率为f，测量矩阵降维倍数为t。压缩加密过程如下所示:

(1)产生混沌序列。

为了抵抗明文攻击，将原始图像作为SHA-256哈希函数的参数，得到256位哈希值D,将D转化为32个十进制数，表示为di,如式(7)所示：

D={di},i=1,2,…,32

(7)

通过式(8)计算过渡参数X,Y,Z,H,W:

(8)

其中，sum(·)表示求和。

通过式(9)计算超混沌Bao系统初始值x0,y0,z0,h0,w0:

(9)

其中,floor(·)表示取整，对于不同的原始图像，混沌系统的初始值完全不同，可以达到一图一密的效果。

将x0,y0,z0,h0设置为超混沌Bao系统初值，w0设置为Logistic混沌初值产生混沌序列。为了获得更好的随机性，丢弃超混沌序列前1 500个元素，取剩下的元素组成4个超混沌序列{Xi},{Yi},{Zi}和{Hi}。利用式(10)将这4个超混沌序列转化成整数序列:

(10)

其中,{Xi}和{Yi}决定DNA编码方式，有8种，分别为X1～X8,Y1～Y8;{Zi}决定运算方式，有4种,分别为Z1～Z4;{Hi}表示DNA解码方式，有8种,分别为H1～H8。

将Logistic混沌序列{Wi}转化成0～255的整数序列，再将其转换为M×N的随机矩阵,记为R,如式(11)所示：

R=mod(floor(W*103),256)

(11)

(2)构造测量矩阵。

根据式(4)利用小波变换对原始图像进行稀疏分解，并在频域中表示。对稀疏化后的图像进行Arnold变换。Arnold变换表示如式(12)所示:

(12)

其中,L为稀疏化图像的高，(V,K)为稀疏化图像的像素点的位置坐标，(v,k)为变换后稀疏化图像的像素点的位置坐标。

本文利用克罗内克积性质构造测量矩阵，提出的压缩感知框架表示如式(13)所示：

(13)

其中，I_A为稀疏化后的Arnold变换图像；P为t×t的随机高斯矩阵;t为降维倍数，如式(14)所示：

(14)

通过随机高斯矩阵P，可把低维的测量矩阵Φ1和Φ2扩展为高维测量矩阵。根据式(6)可得到式(15)：

(15)

因此,Φ1⊗P的大小为(m×t)×(n×t),也就是M×N。假设原始图像大小为256×256，图像压缩率f=M/N=m/n=0.75，则传统的压缩感知测量矩阵维度为192×256。本文对测量矩阵进行降维处理，设降维倍数t=4，则测量矩阵维度为48×64,极大减小了测量矩阵所需的存储空间，提高了传输效率。

(3)获得压缩图像。

根据式(13)得到一个压缩后的M×N测量值图像，记为CS_I。

(4)DNA编码。

把矩阵R和矩阵CS_I分成个数相同、大小相等的若干子块。利用整数序列{Xi}和{Yi}分别对矩阵R和矩阵CS_I的子块进行DNA编码，整数序列{Zi}决定子块之间的DNA运算方式。

对运算完成后的子块进行DNA解码，整数序列{Hi}决定子块的DNA解码方式。

(5)获得加密图像。

合并所有子块得到大小为M×N的加密图像，记为E。

解密过程如下所示：

(1)输入密钥。

输入超混沌Bao系统初始值x0,y0,z0,h0和Logistic混沌系统参数u和初值w0。

(2)产生混沌序列。

通过输入的密钥产生混沌序列{Yi},{Zi},{Hi}和{Wi},将其转化为混沌整数序列并得到二维随机矩阵R。

(3)DNA逆编码。

将加密图像E和矩阵R分块,与加密时产生的子块大小相同。对加密图像E和矩阵R的子块进行DNA逆运算，运算法则由整数序列{Zi}决定。合并所有子块，得到解密后的测量值图像CS_I,将CS_I的稀疏度记为ks。

(4)获得重构图像。

将矩阵CS_I测量矩阵Φ1、Φ2和稀疏度ks作为输入调用OMP重构算法，得到测量前稀疏信号的估计值。最后对该估计值进行小波逆变换和Arnold反变换得到原始图像的重构图像I′，其大小为N×N。

4 仿真实验与结果分析

4.1 仿真实验

本文选择“Lena”“Couple”和“Watch”3幅256×256的灰度图像作为测试图像，仿真软件为Matlab2016b，设置超混沌Bao系统参数a=20，b=4,c=32,d=4。Logistic混沌系统参数为u=3.9999，压缩率为0.85。仿真结果如图3所示，其中图3a,图3d和图3g为原始图像，图3b,图3e和图3h为压缩加密图像，图3c,图3f和图3i为重构图像。

Figure 3 Simulation results图3 仿真结果

从图3可以看出，压缩加密图像的大小不等于原始图像的大小，且重构图像与原始图像在视觉上并没有明显区别，表明该压缩加密算法效果良好。

4.2 直方图分析

直方图用于描述灰度级对应的像素数和每个灰度级出现的频率，显示图像像素的分布规律，是衡量图像加密算法性能的重要指标之一。图4a～图4f为3幅测试图像加密前后的直方图。

从图4可以看出，原始图像的直方图均起伏不定，而加密图像3个通道的直方图均分布平坦，具有伪随机性，可隐藏原始图像的统计特性，从而可以有效抵御大规模针对图像的基于直方图的统计攻击。

4.3 相邻位置像素值关联性分析

图像抵御攻击的能力与其相邻位置像素值的关联性呈反比关系。为了测试图像的抗攻击能力，本文分别随机选取不同图像水平、垂直和对角线方向相邻的5 000对像素点进行分析。相关性系数的计算如式(16)所示：

(16)

其中，xi和yi为位置相邻的像素值，j为所取像素点对数5 000。表4给出了不同明文图像和密文图像的水平、垂直和对角线相邻像素的相关系数。可以看出，原始图像的水平、垂直和对角线方向的相关性系数均接近1，说明其相邻位置像素值关联性很大。而加密图像的相关性系数均接近0，说明加密图像的水平、垂直和对角线方向的相邻位置像素值基本无关联性。

表5是本文算法与其他加密算法的相关系数对比结果。实验结果表明，本文算法可以大大降低相邻像素的相关性，加密后图像的混乱程度更高一些。本文算法优于所比较的其他加密算法。

Table 4 Correlation coefficients of adjacent pixels of different images

Figure 4 Histograms of test iamges before and after encryption图4 测试图像加密前后直方图

Table 5 Comparison of correlation coefficients of adjacent pixels

4.4 压缩性能分析

峰值信噪比PSNR(Peak Signal to Noise Ratio)和均方误差MSE(Mean Square Error)是评价图像质量的客观标准。本文使用PSNR来衡量原始图像与重构图像之间的差异。PSNR和MSE的计算公式分别如式(17)和式(18)所示:

(17)

(18)

其中,M×N表示图像的大小，R(i,j)和F(i,j)分别表示原始图像和重构图像在(i,j)处的像素值。

表6为不同压缩率下的PSNR值。从表6中可以看出,PSNR值越小，图像失真越大。当压缩比为85%或75%时，恢复图像与原始图像基本相同。当压缩比为50%时，PSNR值较小，重构后的图像质量在一定程度上可以接受。因此，本文算法具有良好的压缩性能，可以减少在网络中传输的图像负载。

Table 6 PSNR values with different compression ratios

4.5 信息熵分析

本文利用信息熵评价图像像素值的混乱程度。像素分布越均匀，信息熵越大,且越接近理想值8。本文根据式(19)计算加密图像的信息熵值:

(19)

其中，xi表示像素值，p(xi)表示像素值xi出现的概率。

根据式(19)计算得到的3幅加密图像的信息熵值如表7所示。由表7可知，加密图像的像素分布更具随机性,且与理论信息熵最大值8非常接近,能有效抵抗信息熵攻击。

Table 7 Information entropy of different images表7 不同图像的信息熵

4.6 密钥空间分析

本文使用了超混沌Bao系统参数初始值x0，y0，z0，h0及Logistic参数u和初始值w0作为密钥，共6个密钥。考虑到计算精度为1015,则密钥容量为(1015)6=1090≈2276。这是一个巨大的密钥容量，足以抵抗基于穷举密钥的方式来破解图像。表8给出了本文算法与其他算法的密钥空间对比。

Table 8 Comparison of key spaces

4.7 抗噪声能力分析

图像在传输过程中易受到噪声的干扰和破坏。为了评估所提出的压缩加密算法的抗噪能力，本文在加密图像中加入不同程度的高斯噪声和椒盐噪声，重构得到的图像，如图5和图6所示。

Figure 5 Reconstructed images by adding different degrees of Gaussian noise图5 加入不同程度的高斯噪声得到的重构图像

Figure 6 Reconstructed images by adding different degrees of salt pepper noise图6 加入不同程度的椒盐噪声得到的重构图像

由图5和图6可知，随着加入噪声的强度增大，图像越来越模糊，但从直观视觉上仍然能够分辨出原始图像的主要信息，说明此压缩加密算法抗噪声能力较强。

4.8 抗裁剪能力分析

加密图像受到裁剪攻击时，需要最大程度地保留其细节信息，将裁剪对图像整体的影响降到最低。图7a为加密图像受到裁剪攻击后，数据丢失了一部分。图7b为其对应的重构图像。可以看出，加密图像被部分裁剪破坏了，重构图像在一定程度上发生了变形，但此算法最大程度上降低了裁剪对局部的影响，可以恢复大部分原始信息。这表明本文算法抗裁剪攻击性能较强，适用于包含细节信息图像的加密。

Figure 7 Anti cutting test图7 抗裁剪测试

4.9 运行效率分析

本文算法先对原始图像进行压缩，再进行加密，缩小了待加密图像大小，提高了加密效率。进一步地，与传统压缩感知加密算法不同的是构造测量矩阵的方式。传统的压缩感知加密算法生成的测量矩阵维数高，在传输时会占用更多的带宽和空间。本文算法通过KP将低维矩阵扩展为高维矩阵，提高了传输效率并缩小了存储空间。

为了更直观地描述所提出的图像加密算法的速度,通过Matlab2016软件记录加密和解密时间。使用的电脑配置为：Intel Core i5-4460 CPU，8 GB内存，操作系统为Windows 7。表9是压缩率为0.5的情况下，加密和解密不同尺寸的图像所花费的时间。从表9可以看出,图像尺寸越大，加密和解密花费的时间越长。

Table 9 Encryption time and decryption time of different images

表10为在加密解密大小为256×256图像上与传统压缩加密算法的时间对比。通过对比可知，本文算法加密解密时间短，效率高，可实时地实现图像加密和解密。

Table 10 Comparison of encryption time and decryption time

4.10 抗差分攻击能力分析

安全的加密算法对明文图像的任何变化都十分敏感，研究人员通常用像素改变率NPCR(Number of Pixels Change Rate)和统一变化强度UACI(Unified Average Changing Intensity)测试加密算法的抗差分攻击性能。其计算如式(20)和式(21)所示：

(20)

(21)

其中，M和N为图像的高和宽,C′和C为2幅对应明文图像只有1个像素不同的压缩加密图像。若C′(i,j)=C(i,j)，则D(i,j)=0，否则D(i,j)=1。对于8位灰度图像，NPCR和UACI的理想值分别为99.609 4%和33.463 5%。不同图像的测试结果如表11所示。

Table 11 NPCR and UACI of different images

由表11可知，本文算法对图像微小变化很敏感，且3幅图像的NPCR和UACI的平均值分别为99.600 1%和33.462 4%，十分接近期望值。

表12为本文算法和其他文献算法在对相同Lena图像进行加密时NPCR和UACI的对比。由表12可得，本文算法具有良好的抗差分能力。

Table 12 Comparison of NPCR and UACI of different algorithms

5 结束语

针对传统单一图像加密算法安全性能差和传输效率低等问题，本文提出了一种基于压缩感知和DNA编码的图像加密算法。首先，高维超混沌系统保证了高复杂性和高随机性的优点。其次，采用原始图像作为SHA-256哈希函数参数，生成混沌系统初始值以抵抗明文攻击。接着，采用DNA编码技术保证了图像加密算法的安全性。最后，通过KP构造测量矩阵，将低维矩阵扩展为高维矩阵，减小了观测矩阵所需的存储空间，提升了算法的传输效率。仿真实验与结果分析表明，本文算法压缩性能良好,运行效率高，重构图像能够保留原始图像的大部分有效信息且能够抵抗噪声攻击、裁剪攻击和差分攻击，保证了图像传输时的安全性和快速性。