求解时变非线性方程的Adams-Bashforth离散时间算法

孙 敏，葛 静

(枣庄学院 数学与统计学院，山东 枣庄 277160)

0 引言

方程的概念与方法已经应用到自然科学与社会科学的各个领域，在生产生活中有着广泛的应用，可以描述经济、管理、物理、工程与社会科学等领域中的许多问题。比如，在管理领域中的互补问题及变分不等式问题，通过投影算子可以转化成一个非线性方程[1]；在物理领域中的Poisson问题，通过区域离散化及导数的差商近似可以转化成一个线性方程[2]。寻找非线性方程的解析解与数值解已经成为数学与物理的一个重要研究课题[3]，相应的研究成果浩如烟海，比较经典的有求解线性代数方程的Gauss消去法、直接三角分解法、Jacobi迭代法、超松弛迭代法与共轭梯度法，以及求解非线性方程的不动点迭代法、Aitken加速法、Newton迭代法与割线法等[3-4]。

目前，学术界主要研究时不变非线性方程，由于时不变线性方程没有考虑时间参数，因此其不能细致地描述时变问题[5]。相比于时不变问题，时变问题是自然科学领域里更常见的一类问题。比如，对于冗余机械臂路径规划的实时控制问题，在每个时刻点，末端执行器的位置是不同的，设计者需要根据末端执行器的位置实时确定连杆的角度，因而该问题是一类时变问题。为了更稳健地完成路径规划，Zhang等[6-8]进行了系统的研究，建立了该问题的时变非线性方程模型、时变二次规划模型等，并提出了一系列求解算法，包括梯度神经网络、零化神经网络、递归神经网络、原始-对偶神经网络、零化-梯度神经网络等，并对这些神经网络的离散格式进行了系统研究。另外，Sun等首先对离散化后的零化神经网络的步长有效区间进行了研究。在文献[9]中，Sun等给出了零化神经网络的五步离散格式，并借助Jury稳定判据研究了该离散格式步长的有效区间。

文献[5-9]所提出的零化神经网络的离散格式都属于线性多步法，这些方法只使用了当前迭代点处函数的信息，没有使用前几步迭代点处函数的信息，但是信息利用得越充分越能够提升算法的效率与精度。本文将继续对零化神经网络的离散格式进行研究，提出了一类求解时变非线性方程的六步Adams-Bashforth离散算法，该算法充分利用了前面六步函数的信息。利用Jury稳定判据，研究了Adams-Bashforth离散算法步长的有效区间。最后，将所提出的算法应用到机械臂路径规划问题，得到了较好的数值效果。

1 预备知识

本文研究如下时变非线性方程问题(TVNE)：求x(t)∈Rn满足

F(x，t)=0，t∈[0，tf]

(1)

式中：F：Rn+1→R关于变量x，t可导，tf>0表示所研究对象的最终时间节点。对问题TVNE做如下假设。

假设1 问题TVNE是可解的。

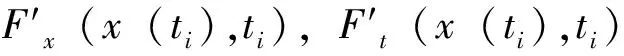
Jury稳定判据可以用来判断一个线性离散时间系统的稳定性。对于一个线性离散系统来说，如果其特征方程是

Q(z)=anzn+an-1zn-1+…+a1z+a0

(2)

式中an>0，那么相应的Jury稳定判据见表1。

表1 Jury稳定判据

表1的第1、2行是Q(z)的系数，从第3行开始按下面的公式计算

定理1[10]特征多项式(2)所对应的线性离散系统是稳定的，也就是Q(z)的零点全都落到单位圆中，当且仅当下面的条件成立：

Q(1)>0，(-1)nQ(-1)>0，b0>0，c0>0，d0>0，…，l0>0，r0>0，t0>0.

2 Adams-Bashforth离散时间算法

定义向量值误差映射ε(t)=F(x(t)，t)

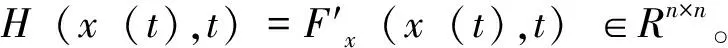
(3)

这是一个一阶常微分方程，可以使用常微分方程的数值方法求解，比如欧拉方法、龙格-库塔方法等。将问题(3)的右端记为f(x，t)，则问题(3)可以改写成

(4)

线性多步法是求解问题(4)的一类有效方法，其一般形式是

式中：αj，βj是常数，αk=1，|α0|+|β0|≠0。对于任意给定的整数k>0，常数αj、βj可以通过求解下列的线性方程组得到

(5)

下面推导一个具体的六步Adams-Bashforth格式。令k=6，以及α0=α1=α2=α4=α5=β6=0，α6=1。

由(5)式得

(6)

线性方程组(6)有7个未知数，指定β0=-51/160，于是由(6)式可求得

将这些参数代入C6得

C6=(36α3+66)/6!-(β1+25β2+35β3+45β4+55β5)/5!=0

于是得到一个六步Adams-Bashforth格式

(7)

其截断误差是

定理2 六步Adams-Bashforth格式(7)的绝对稳定区域是：

R≈(0，0.0921)

根据六步Adams-Bashforth格式(7)得到求解问题(4)的六步Adams-Bashforth格式

(8)

式中：h=τγ是步长因子。于是根据定理2得到h的有效区间是R≈(0，0.0921)。

3 应用

在位置层面上，二连杆平面机械臂的离散时间运动方程是

F(θ)=ra

式中：F(·)是结构已知的运动映射，其定义为

式中：li是第i个连杆的长度，c1=cos(θ1)，s1=sin(θ1)，c2=cos(θ1+θ2)以及s2=sin(θ1+θ2)。另外θ=[θ1，θ2]T∈R2表示两个连杆关节角度构成的2维列向量，ra∈R2是末端执行器的实际坐标。

根据上面的描述可以得到路径规划问题的时变非线性方程

ra=rd

(9)

式中：rd∈R2是末端执行器的期望轨迹坐标。在本试验中，取li=2，i=1，2，规划的路径是Lissajous曲线，即

利用离散时间算法(8)来求解时变非线性方程(9)。由于(8)是六步方法，前五步采用两步法来计算前面的迭代点。初始化的角度θ0=[0，π/3]T，执行周期tf=10秒，采样周期τ=0.005，步长h=0.05。计算结果见图1与图2，其中e1=|ra(1)-rd(1)|，e2=|ra(2)-rd(2)|。

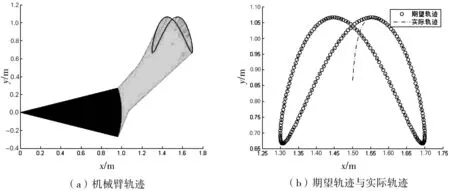
图1 平面轨迹

图2 水平与垂直方向轨迹误差

由图1与图2可以看出，离散时间算法(8)很好地完成了本次路径规划任务，在水平与垂直方向轨迹误差很快达到了10-14m。

4 结论

本文对时变非线性方程进行了研究，设计了一类六步Adams-Bashforth离散时间算法。基于Jury稳定判据，对该算法的步长进行了理论分析。最后将该算法应用到解决路径规划问题中，得到了高精度的路径规划方案。