蚁群算法在通勤班车路径优化中的应用

□文/薛雨石

（北京科技大学 北京）

［提要］结合北京市优质教育资源向雄安布局发展背景，本文提出如何规划通勤班车的最优路径，使得既方便教职员工往返于新校区与宿舍之间，又能为学校节约运行成本，把现实中的班车路径优化问题巧妙地转化为求解容量受限的车辆路径问题。最后，利用蚁群算法的优点，通过蚂蚁个体间的信息交流与传递找到最优解，并用MATLAB程序实现如下算例：新校区周围有20个停靠车站，350位职工具有通勤接送需求，班车运行线路以新校区作为线路的起点和终点，每个车站只能被访问一次。每辆班车的载荷上限为60人，各车站的人数和地理位置分布以数据的形式被程序调用。模型支持根据需求变化动态调整各参数，为管理者提供可靠的决策依据。

党中央提出京津冀协同发展、有序疏解北京非首都功能背景下，北京市一批优质的教育资源正在通过整体搬迁、办分校、联合办学等多种方式向雄安新区布局发展。研究如何打造一个宜业宜居的新城市、新校区，吸引人才向新区集聚，为人才提供完善的生活配套措施和便利的公共交通条件，打造快捷、便利、绿色、安全的出行环境十分具有理论价值和实际意义。本文通过蚁群算法这一智能算法优化，以通勤班车的路径优化与停靠车站的定位布局为研究对象，求解出多目标非线性整数规划模型的最优解，为智慧宜居提供可靠的决策依据。

一、容量受限的车辆路径问题描述

经典车辆路径问题（VRP）最早是由Dantzig和Ramser于1959年提出，它是指有若干辆车，对若干个具有货物需求的顾客进行配送，车辆必须从配送中心出发，完成配送任务后再回到配送中心，并且所有顾客只能被访问一次，不能重复，求实现上述问题的最短路径配送方案。容量受限的车辆路径问题比经典VRP的多一个约束条件：每条配送路线上顾客需求总量不能超过车辆的载荷上限。

假设vi（i=1，2，…，n）表示顾客所在地，v0表示配送中心，dij表示vi到vj的距离，每个地点的配送需求量为qi，共有K辆车执行配送任务，每辆车的载重量为Qk（k=1，2，…，K）。

用nk代表第k辆车配送第n个顾客所在地，nk=0表示该点未使用第k辆车。

CVRP可建立如下模型：

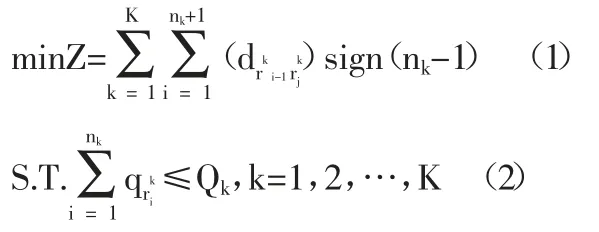
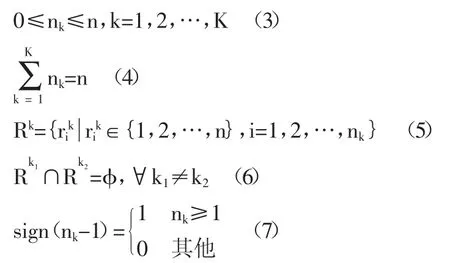
式（1）为目标函数，求各条配送路径距离之和的最小值；式（2）为约束函数，每条配送路径上顾客需求总量不超过车辆的载荷上限；式（3）为约束函数，每条配送路径上顾客点数不超过总站点数；式（4）保证每个顾客点都得到配送服务；式（5）表示每条配送路径上顾客点的组合及排序；式（6）保证每个顾客点仅能被一个车辆完成配送；式（7）表示被访问的顾客点值取1，未被访问的点值取0。

二、蚁群算法介绍

蚁群算法是意大利学者M.Dorigo受到自然界中真实蚂蚁集体觅食行为的启发，于1991年首次提出的一种基于蚂蚁种群的智能优化算法。蚂蚁个体之间是通过一种叫信息素的物质进行信息传递和交流的，每只蚂蚁在移动过程中都能释放信息素，并且感知到其他蚂蚁留下的信息素，以此指导自己的运动方向。某一路径上走过的蚂蚁越多，后面的蚂蚁选择该路径的概率就越大，通过这种信息的正反馈，能够选择最优的路径实现搜索食物的目的。由于蚁群算法在解决组合优化问题中取得了满意的实验结果，因此逐渐被应用到实际工程问题中，通过模仿生物的特性，更好地为人类服务。

（一）蚁群算法优点。（1）蚁群算法通过多个个体间的合作，信息不断地传递与交流，可很快收敛于解空间的某一子集，有利于发现较好解。（2）蚁群算法采用了正反馈原理，不易陷入局部最优解。（3）蚁群算法易于与其他启发式算法结合，以改善算法的性能。

（二）人工蚂蚁与真实蚂蚁的相同点。通过对真实蚂蚁行为的观察，将蚁群觅食行为中最关键的部分赋予人工蚂蚁：真实蚂蚁可以在没有任何提示的情况下找到从食物源到巢穴的最短路径，并且能在原有路径上出现障碍物后，自动搜索新的最佳路径。

1、人工蚂蚁和真实蚂蚁都可以改变当前的环境：真实蚂蚁在经过的路径上留下信息素，人工蚂蚁则会改变所经路径上存储的数字信息。这一机制就是控制论中正反馈概念的应用，即以现在的行为去强化未来的行为。通过这种正反馈，蚂蚁个体可以通过相互协作在全局范围内找出最优解决方案。虽然每只蚂蚁都能够建立一个解决方案，但是高质量的解决方案是整个蚁群合作的结果。

2、人工蚂蚁和真实蚂蚁有着共同的任务：寻找起点（蚁穴）至终点（食物源）的最短路径（最小代价）。真实蚂蚁和人工蚂蚁都不具有跳跃性，它们只能沿着相邻节点一步步地移动，直至遍历完所有节点。

3、人工蚂蚁与真实蚂蚁从一个节点移动到下一节点都是通过对信息素浓度的判断而选择策略，信息素浓度越高，选择的概率越高，反之亦然。

（三）人工蚂蚁与真实蚂蚁的不同点。为了更有效地解决实际问题，人工蚂蚁具有真实蚂蚁所不具备的本领：（1）人工蚂蚁的选择策略与时间无关。（2）人工蚂蚁的每次移动会改变路径记录表，以记录当前的移动坐标。（3）人工蚂蚁不是完全盲从的，每次迭代会产生一只最优蚂蚁，对信息素浓度矩阵进行加强，以便下一次迭代解的优化。

三、蚁群算法求解步骤

（一）确定蚂蚁的下一个访问点。为了把求解步骤描述清楚，先给出一个简化的算例：假设有三个停靠车站，每个车站预计分别会有10位、20位、30位乘客上车，每辆车最多可以承载30人，从新校区0点发车，接完全部乘客后再回到0点。新校区与三个车站的坐标如表1，位置图如图1所示。（表1、图1）

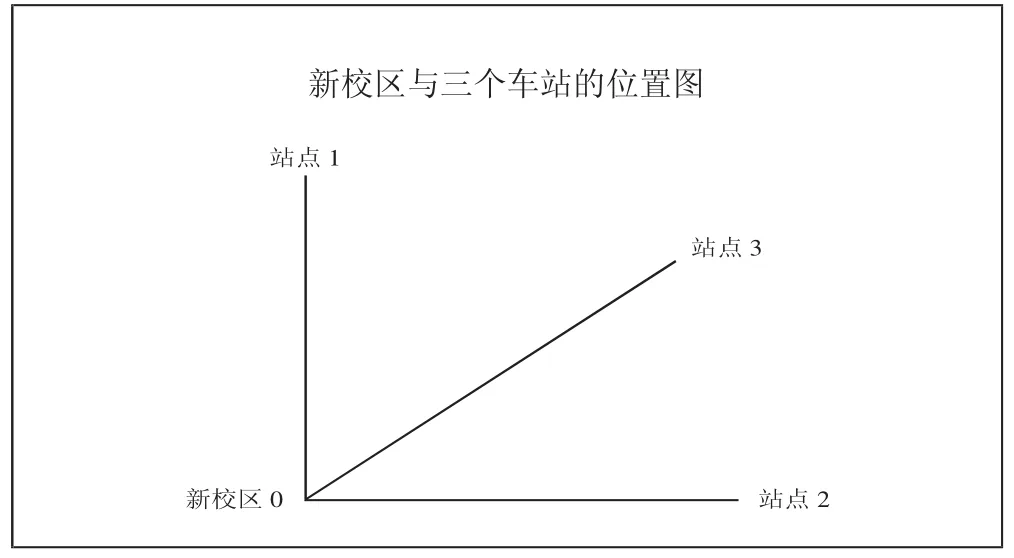
图1 新校区与三个车站的位置图

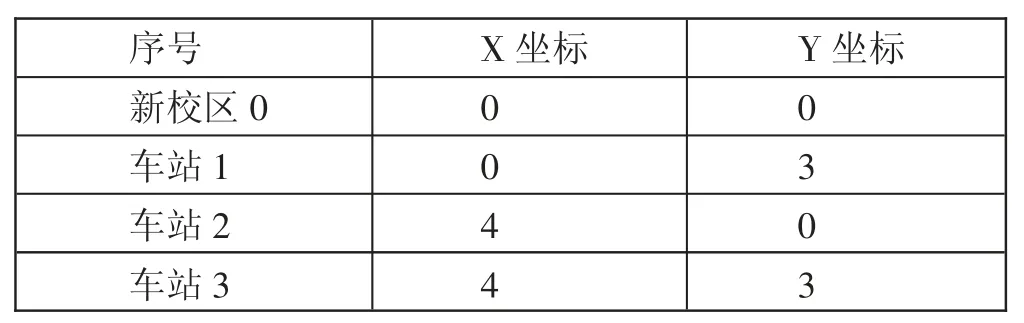
表1 新校区与三个车站的坐标一览表

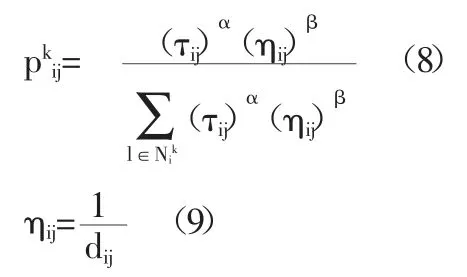
根据式（7）、式（8）得出，蚂蚁1从新校区到车站1、2、3的概率分别为：

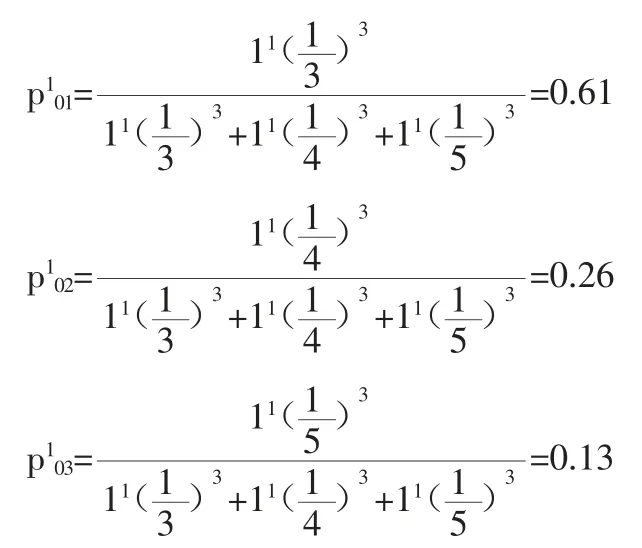
（二）构建蚂蚁行走路线。根据公式计算出的概率构建轮盘赌转盘，概率越大面积越大，被选中的可能性越高。假设蚂蚁1从新校区出发，初次选中车站2，按照规则车站2的20位乘客全部上车，把车站2添加进路径集合的表达式为［0，2］。接下来蚂蚁1从车站2选择下一个车站，需要考虑每辆车有30人的最大承载量，车站3因有30位乘客而不满足约束条件，蚂蚁1只能选择路径至车站1，车站1的10位乘客全部上车，符合约束条件，最后返回新校区，此时蚂蚁1的第一条行走路线上的路径集合点表达式为［0，2，1，0］。

蚂蚁1在返回新校区后还有车站3未访问，任务并未完成，因此蚂蚁1还需要构建第二条行走路线，路径集合点表达式为［0，3，0］，蚂蚁1的任务执行完毕。

蚂蚁1构建完成了一个完整的路径方案，里面包括若干条行走路线内所有的车站都已完成一次遍历，有几条行走路线就代表要派出几辆车完成通勤任务。上述完整路径方案为［2，1，3］，根据该方案更新信息素浓度矩阵。

（三）更新信息素浓度矩阵。假设最大迭代次数设置为100次，每次迭代有50只蚂蚁构建路径方案。当50只蚂蚁遍历完所有的城市，就完成了一次循环。为了避免残留的信息素过多，淹没了启发信息，降低了启发函数的作用，因此规定实现完整路径距离TD最短的蚂蚁为本次迭代下的最优蚂蚁，它将在其经过的每条路径上留下信息素。最优蚂蚁会对信息素浓度矩阵进行修改，公式如下：

其中，ρ为信息素的挥发因子，1-ρ就表示信息素挥发后的残留系数。为了避免找到一个局部最优解而不再向全局最优的方向做进一步搜索，因此有必要在蚁群算法中设计一种挥发机制，类似于真实信息素的挥发。这种机制可以使蚂蚁逐渐忘记过去，不会受到以前经验的过分约束，从而指引蚂蚁向着新方向进行搜索，避免过早收敛。Q为蚂蚁构建一次完整路径所释放的信息素总量，Q值越大，算法的收敛速度越快。TD为计算值，代表蚂蚁构建一次完整路径所行驶的总距离。

本文初始假设ρ=0.2，Q=5，第一次迭代的最优蚂蚁TD=12+10＝22。

因为有起始点新校区0和3个遍历点车站，信息素浓度矩阵是一个4×4的矩阵，且矩阵上的初始值τij均为1。根据式（10）、式（11）、完整路径方案［2，1，3］，需要修改信息素浓度的点分别为 τ02、τ21、τ13、τ30，得出信息素浓度矩阵为：

蚁群算法求解CVRP问题的流程如图2所示。（图2）

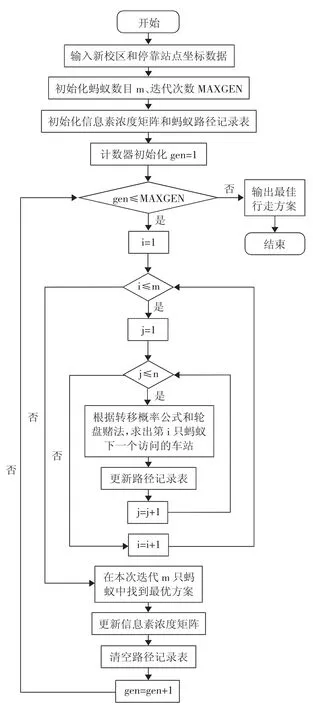
图2 蚁群算法求解CVRP问题流程图

四、实证分析

为了更好地接近现实中的通勤班车路径优化问题，本文在新校区半径15公里的通勤圈内随机选取了20个停靠车站，每辆车都要从新校区出发，最后带着乘客返回新校区，最优路径要求每个车站只能被1辆车访问。为了满足每车载荷上限60人的约束条件，需要事先统计好各站点拟上车的人数，具体如表2所示。算法在MATLAB 2014B上编译执行，初始设置50只蚂蚁和50次迭代计算。（表2）

表2 发车起始点、车站坐标位置与各站点拟上车人数一览表

如果没有计算机辅助执行智能优化算法，完成50只蚂蚁、50次迭代的信息素浓度矩阵更新、转移概率等计算，仅依靠人工几乎不可能实现，通过计算机执行结果如图3所示。（图3）

图3 蚁群算法求解班车最优路径线路图

在可接受的计算时间内，用6辆班车完成了350人次的接送任务，行驶最短总距离215.20公里，并完美地给出了最优路径规划方案。行驶路线如下：

行驶路线1：0→13→17→19→0

行驶路线2：0→15→18→0

行驶路线3：0→16→14→12→0

行驶路线4：0→5→1→2→4→0

行驶路线5：0→3→7→6→9→0

行驶路线6：0→8→11→10→20→0

综上，蚁群算法是一项具有通用性广、理论依据可靠、推导过程严谨等优点的智能优化算法，对每一次迭代的最好解都在不断地加强进化。通过实证分析，本文构建的模型可以有效地帮助管理者科学决策，规避人类所无法避免的非理性判断。同时，模型还支持动态调整停靠车站的位置坐标，既实现了对空间格局、功能布局的刚性约束，又实现了为需求变化提供弹性的可塑空间；既节约了班车运行成本，又最大限度地减少了职工长距离通勤，实现了打造新城市新校区宜业宜居的目标。