基于正交试验的静压径向气体轴承数值分析*
2022-09-21邱春雷田洪雨张开鑫
邱春雷 段 翔 田洪雨 张开鑫 尹 洋
(西华大学机械工程学院 四川成都 610039)
高速旋杯式静电喷涂是汽车车身的重要涂装方式,气动涡轮作为驱动装置广泛应用于高速旋杯静电喷涂系统[1]。气动涡轮的核心部件为静压气体轴承。静压气体轴承具有精度高、速度高、寿命长和摩擦功耗小4大优点,在精密工程领域中有着十分广阔的应用[2]。文献[3]利用FLUENT仿真软件研究了节流孔直径和气腔尺寸对轴承力学性能的影响,但并未探讨影响的主次因素。文献[4]采用有限差分法计算轴承的气膜压力分布,分析承载力、刚度、质量流量随轴颈转速的变化规律,但未对节流器参数进行全面分析,且没有深入研究更高转速下的动态性能。文献[5]研究了不同偏心率和供气条件下,节流孔附近的气膜流场特性及承载力变化,并通过优化节流孔出口锥角,提高了承载性能,但未提到刚度及质量流量的变化。文献[6]运用仿真实验研究了小孔节流器导向锥角对轴承性能的影响,研究表明,锥角大小对承载力、刚度等均有影响,但影响程度较小。文献[7]研究了单个节流器中微孔个数与尺寸对轴承微振动特性的影响,研究表明,采用多个微孔可显著减小微振动。但该文献没有深入分析不同微孔个数与尺寸下轴承的承载性能。文献[8-9]利用数值计算方法和仿真研究了轴承参数及外部参数对承载力的影响。文献[10]采用遗传算法的多目标优化对多孔矩形静压气体轴承的节流器参数进行了优化,以提高轴承力学性能,其独到之处在于节流孔数量和位置完全自由,可根据需求进行选择。文献[11]研究指出在节流孔间设置沟槽,可以显著减小气体的周向流动,提高轴承的承载性能。
从以往的文献看,对静压气体轴承的研究主要集中在不同参数对轴承承载力的影响规律上,对承载力、刚度、质量流量的综合性能的比较研究较少,各个参数的影响程度往往被忽略。本文作者利用工程数值计算方法求解静压径向气体轴承性能,运用正交试验法分析轴承综合性能以及各参数对承载特性的敏感性,以优化轴承性能。
1 静压径向气体轴承的工程计算法
1.1 轴承模型
静压径向气体轴承以空气作为润滑介质,从外部输入供气压力,通过节流孔使轴承间隙充满气体,形成具有一定压力的气膜。由于转轴的自重及所承受的载荷,使轴承与转轴轴线不重合,有偏心距e,在载荷方向上造成气膜厚度不同,就会存在压力差,这种压力差使气膜具有一定承载力和刚度,达到支撑效果,如图1所示。
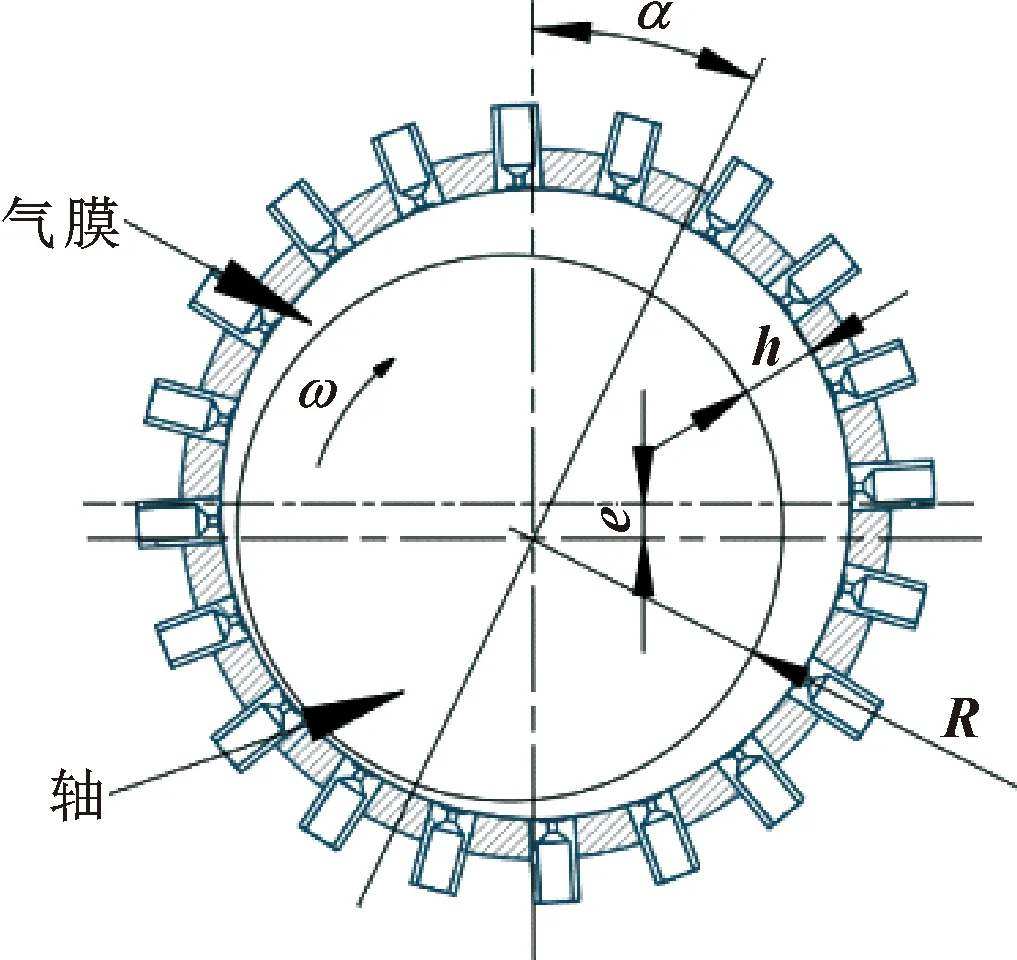
图1 静压径向气体轴承模型
1.2 气体轴承的数值计算
由于气膜厚度远小于轴承半径,因此忽略轴承内表面曲率的影响,将轴承气膜展开成平面,如图2所示。
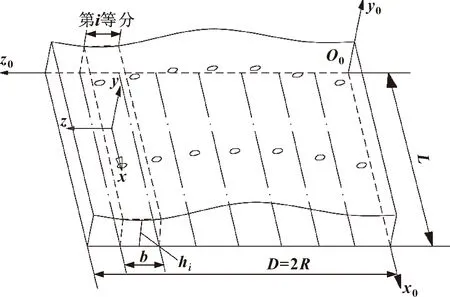
图2 小孔节流气膜展开平面
轴承内各点的压力p符合雷诺方程[12]:
(1)
式中:h为气膜厚度。
式(1)为气膜压力随几何位置变化的表达式,难以求出解析解,可作简化处理得到数值解。将展开的气膜平面按单排节流孔个数在圆周方向上分为n等分,假设每等分的气膜厚度为常数,大小等于节流孔处的气膜厚度hi(i=1,2,…,n)。
对任意等分i进一步假设:
(1)线性气源假设,节流孔间无气体流动,气体在每等分内呈一维流动;
(2)每等分节流孔间压力相等,值为该等分节流孔流出压力pdi;
(3)气体无周向流动,只沿轴向(x方向)流向端面,压力从pdi降至环境压力pa;
(4)气体在气膜内为等温层流流动:
(2)
(5)气体流动为无惯性稳态流动,黏度系数η为常数。
气体运动方程[10]可简化为
(3)
(4)
(5)
式中:u为x方向的气体速度。
质量连续方程为
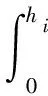
(6)
式中:Mi为第i等分气体质量流量;b为每等分宽度,b=2πR/n。
单个节流孔质量流量为
(7)
(8)
βi=pdi/ps
(9)
式中:θ为流量系数,一般取0.8;ps为供气压力;A为单个孔节流面积;βi为节流压力比;对空气而言βk=0.528,k=1.4。
联立式(2)—(9),通过积分与代入边界条件可得式(10)。
(10)
令:
(11)
ω=f1f2f3
(12)
(13)
hi=h0(1-εcosαi)
(14)
式中:l为节流孔到轴承端面距离;σ=pa/ps;f1为气流通道系数;f2为工作介质系数,常温和一个大气压下的空气f2=2.68×10-4mm;f3为轴承结构系数,f3=l/R;h0为平均气膜厚度;ε为偏心率;αi为过等分中点的半径与基准线的夹角。
第i等分气体的总合力可写成:
(15)
轴承的总承载力为
(16)
联立式(10)与式(12),可得:
(17)
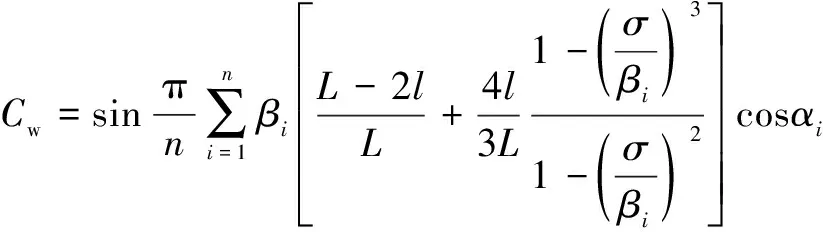
(18)
式中:Cw为无修正承载能力系数。
修正系数:
(19)
修正后得到的气膜的总承载力为
W=CwfwLDps
(20)
气膜刚度为
K=ΔW/Δe
(21)
式中:e为偏心距。
节流孔质量流量为
(22)
1.3 方法验证
为验证所用工程计算方法的有效性,将部分运算结果与文献[13]的计算结果对比。轴承结构参数采用文献中的数值,文献所列结果如图3(a)所示,文中计算结果如图3(b)所示。显然,在3种偏心率下,承载力随平均气膜厚度的变化,文献与文中的计算结果有很好的一致性,只存在微小的差异,说明文中运用的数值方法是可信的。
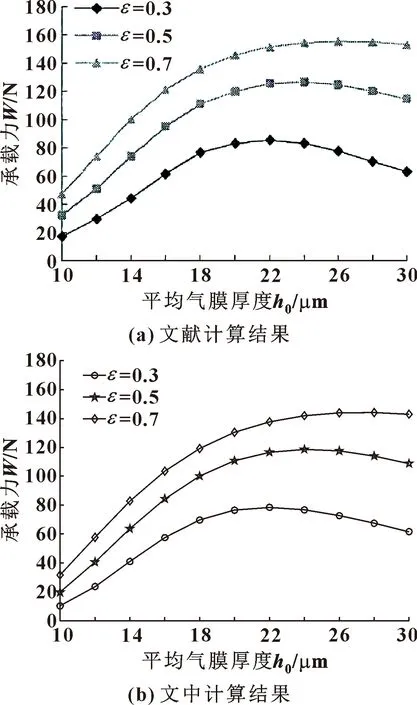
图3 不同偏心率下承载力随平均气膜厚度变化
1.4 轴承性能计算
文中研究的是支承气动涡轮空心转子的静压径向气体轴承。空心转子由一对小孔节流式径向轴承支承,两轴承间间隙s=10 mm,保证轴承两端空气顺利流出外部环境,结构模型如图4所示,静压气体径向轴承结构参数见表1。
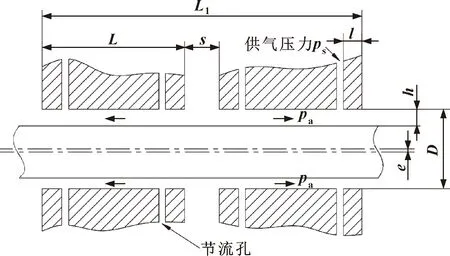
图4 轴承结构
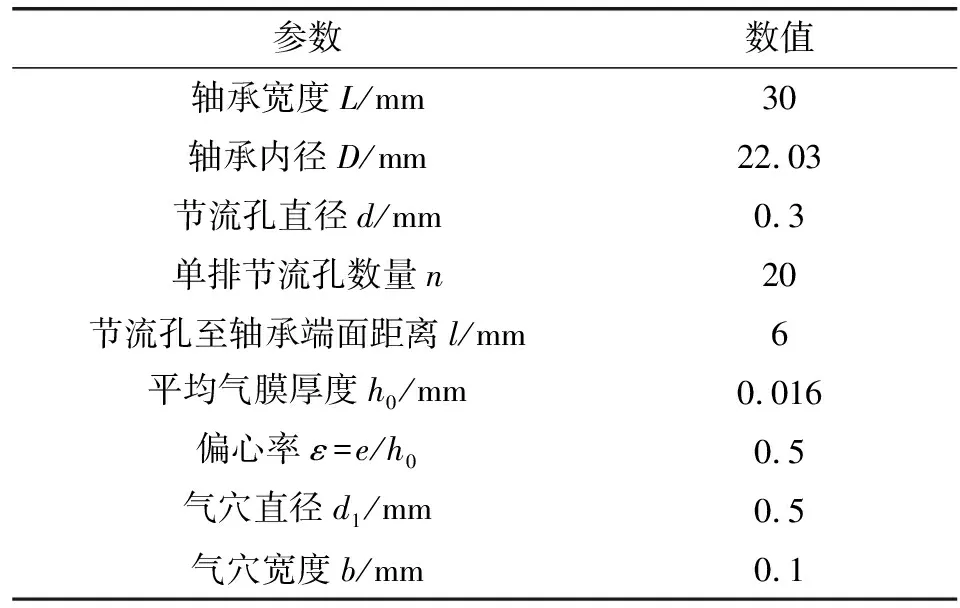
表1 轴承结构参数
设供气压力ps=0.5 MPa,环境压力pa=101 325 Pa。将表1中参数代入式(20)—(22),得到轴承性能,见表2。

表2 轴承性能计算结果
2 正交试验设计
影响轴承性能的参数有轴承几何参数和供气参数,而供气参数与轴承性能呈正相关[14],节流器是轴承的核心结构,节流器结构影响着轴承性能。
2.1 正交试验
正交试验是一种分析多因素多水平的方法,效率高、速度快、试验点代表性强,能够直观看出各因素对目标函数的敏感性[15]。利用正交试验方法,分析节流器结构参数对轴承性能的影响。选择的目标参数有节流孔直径d、节流孔数量n、节流孔至轴承端面距离l、平均气膜厚度h0和偏心率ε。以承载力、刚度、质量流量为目标函数,采用5因素5水平的正交设计,因素变量和正交试验结果见表3、4。
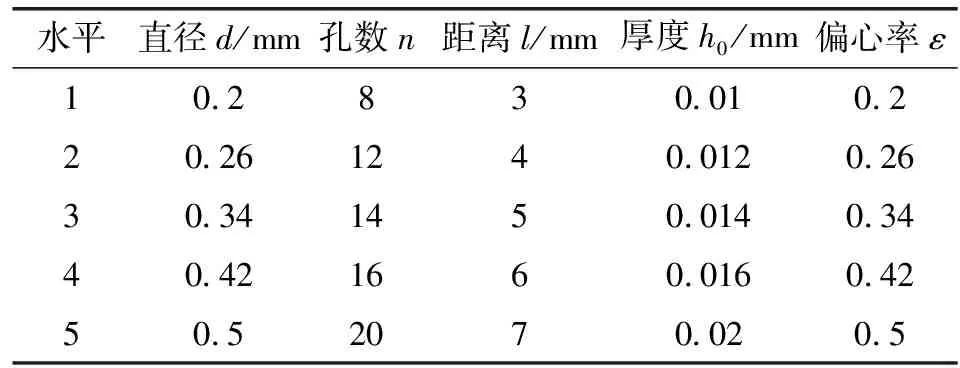
表3 正交试验因素和水平
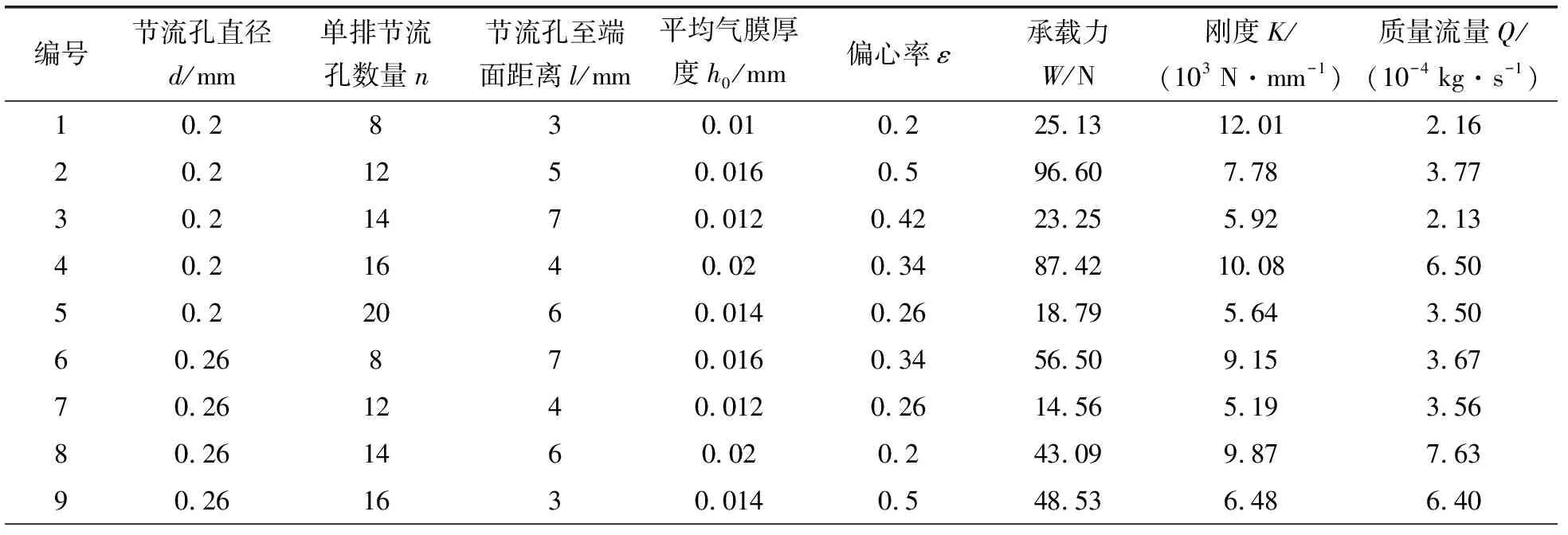
表4 正交试验结果
2.2 结果分析
用T表示某因素某水平试验结果之和:
(23)
式中:i为因素;j为水平;S为试验值;n为水平数量;m为因素数量。
Ta表示某因素某水平试验结果和的均值:
Ta=Tij/n
(24)
如图5所示为各因素的承载力、刚度、质量流量在不同水平下的均值。
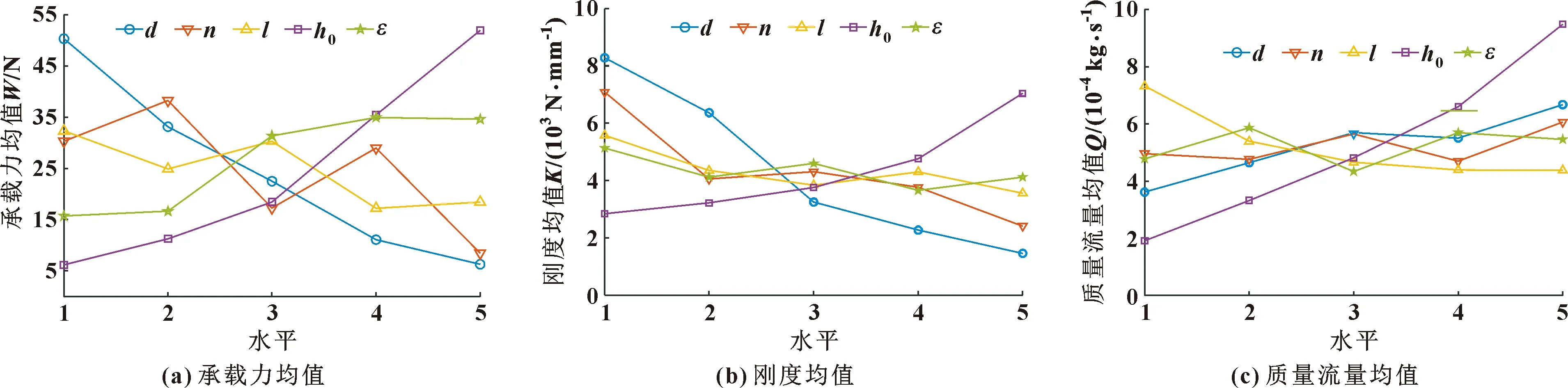
图5 不同水平下各因素均值
从图5(a)中可以看出,承载力均值随平均气膜厚度增大而增大,随节流孔直径增大而减小;平均气膜厚度和节流孔直径变化引起的承载力均值变化幅度明显高于其余参数,说明平均气膜厚度与节流孔直径是影响轴承承载力的主要因素。从图5(b)可看出,刚度随平均气膜厚度增大而增大,随节流孔直径增大而减小,与承载力变化是一致的,其中节流孔直径变化引起的刚度均值变化幅度最高,说明节流孔直径对刚度的影响最显著。从图5(c)可看出,质量流量随平均气膜厚度增大而增大,随节流孔直径增大而小幅增大,其中平均气膜厚度变化引起的均值变化幅度最大,说明平均气膜厚度对气体质量流量的影响最大。
综合图5可知,增大平均气膜厚度,承载性能增大,但同时气体质量流量增大;节流孔直径越小,轴承承载性能越好;其余参数随不同水平呈非单调的变化。
极差表示某因素均值的最大偏差,极差越大,敏感性越大。通过极差分析主次因素,可得到优化的试验方案。极差分析结果见表5。
从表5的极差值可知,不同的目标函数有不同的主次因素,具体为
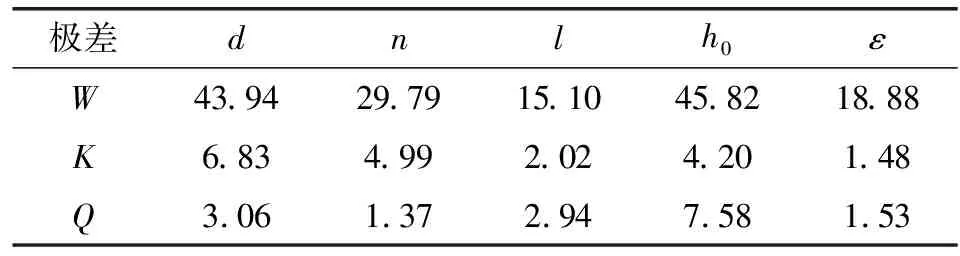
表5 极差分析结果
承载力的敏感性:h0>d>n>ε>l
刚度的敏感性:d>n>h0>l>ε
质量流量的敏感性:h0>d>l>ε>n
根据图5和表5分别以承载力最高、刚度最大和质量流量最小为最优条件,选择某因素最优均值的水平,得到3组最佳组合方案,方案和结果见表6。

表6 优化方案与优化结果
从表6可以看出,与原始方案相比,以不同目标函数为最优得到的结果差异较大。在以承载力、刚度为最优的优化方案中,承载力和刚度均有较大的提升,质量流量均有减少,而以质量流量为最优的方案中承载力太小,不符合设计要求。承载力最优与刚度最优2种方案相比,承载力、刚度和质量流量相差169%、28%和26%,承载力得到了大幅度提高,原因是偏心率越大,气膜厚度差越大,形成的压力差就越大。而2种方案的参数中,只有节流孔数量和偏心率有所不同,而这2种参数都不是影响刚度和质量流量的第一因素,因此2种方案的刚度和质量流量差距较小。综上所述,承载力最优方案综合了承载力和刚度性能,得到的轴承综合性能较好。
为确保轴承静态稳定,即不出现气锤振动现象,气室总容积Vp与气膜体积Vf之间应满足一定关系[16]:
(25)
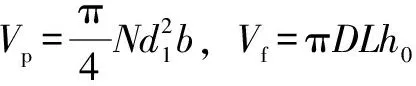
式中:N为节流孔数量,N=24。
将轴承参数代入式(25),得到:
满足静态稳定性要求。
3 结论
(1)分别以承载力最高、刚度最大和质量流量最小为最优条件,对静压径向气体轴承结构参数进行正交试验分析,结果表明,不同的最优条件得到的节流器参数敏感性不同,得到的轴承性能也各不相同。其中,以质量流量为优化目标得到的方案承载性能很差,不符合设计要求;以承载力最优得到的轴承综合性能最好。
(2)平均气膜厚度、节流孔直径和个数是影响轴承承载力和刚度的主要因素。影响气体质量流量的主要因素是平均气膜厚度、节流孔直径和节流孔至轴承端面距离。
(3)研究的节流器参数的最佳组合为节流孔直径d=0.2 mm、单排节流孔数量n=12、节流孔至轴承端面距离l=3 mm、平均气膜厚度h0=0.02 mm、偏心率ε=0.5,该组合参数下轴承性能得到大幅度提升。
