多种面波层析成像方法及其在青藏高原的应用与对比
2022-09-21付媛媛方洪健
李 伦,蔡 晨,付媛媛,方洪健
1 中山大学地球科学与工程学院,广州 510275
2 南方海洋科学与工程广东省实验室(珠海),珠海 519000
3 广东省地球动力作用与地质灾害重点实验室,广州 510275
4 中国地震局地震预测研究所,北京 100036
0 引 言
地震层析成像(seismic tomography)是基于地震仪所记录的地震波各种震相走时、振幅、相位与波形等信息,通过反演计算来获取地球介质的二维或三维速度、各向异性和衰减等物理参数的一种地球物理方法(Aki and Lee, 1976).早在1976年,Aki和Lee(1976)开创性地基于近震初至P波的走时信息,利用最小二乘反演方法构建了美国加利福尼亚地区的三维地壳速度结构,并同时定位了震源的位置.1977年,Aki等(1977)基于挪威地震台网记录的远震信号反演了该区域的岩石圈三维速度结构;同年,Dziewonski等(1977)利用国际地震中心(ISC)记录的全球地震到时信息构建了全球尺度的上地幔三维速度模型.虽然这些工作获取的速度模型分辨率较低,但其开创了三维地震层析成像研究的先河,为后续利用地震层析成像方法构建地球内部速度结构等研究奠定了重要的理论基础与范例.之后的几十年,随着先进地震仪器的研制、地震台网的加密、地震层析成像方法的不断发展与计算能力的提高,地震层析成像在理解地球壳幔结构、深部动力学过程与地震孕震构造等方面发挥了至关重要的作用.
按照所利用的地震震相类型,地震层析成像可分为体波层析成像与面波层析成像.地震面波具有波形振幅较强和易于识别的特点,并且具有频散现象(即对于不同周期的面波,其相速度或群速度的传播速度是不同的,能反映地球内部不同深度的速度结构).从1950年代起,面波就被广泛应用于获取地球介质(尤其是地壳与上地幔)的物理参数信息(如, Anderson, 1987; Ewing and Press, 1954; Forsyth and Li, 2005; Li and Li, 2015;Lin et al., 2009; Montagner, 1985; Nakanishi and Anderson, 1982; Press et al., 1956; Woodhouse and Dziewonski, 1984; Yao et al., 2006).面波可分为瑞利波和勒夫波.瑞利波是P波与SV波干涉所形成,其质点偏振轨迹呈椭圆型,并与水平面垂直;而勒夫波是SH波在层状介质中干涉所形成,其质点偏振方向与地震波传播方向垂直,并只发生在水平方向上.与体波层析成像相比,面波层析成像可同时获取地震波速度的扰动值与绝对值,并且由于其频散特征,不同周期的面波相速度/群速度对地球内部不同深度的速度结构有较好的约束,因此对垂向深部结构具有较高的分辨率.另外,瑞利波与勒夫波数据联合可同时获取剪切波(S波)速度与各向异性信息.但需要指出的是,由于现有的大多数宽频带地震仪能记录的地震信号最长周期为~200 s,使得基于面波数据构建的速度与各向异性模型仅局限于地壳与上地幔深度(400 km以上).另外,由于其水平分辨率很大程度取决于面波的波长与台站的间距,因此其水平分辨率通常比体波层析成像的要低.
面波层析成像方法的发展得益于Press-Ewing地震仪的研制、标准化生产与广泛应用.该类型地震仪器运用了Glitzin的电磁感应器与La Coste的零长度弹簧,对低频的地面运动较为敏感,能够记录长周期的面波信号(Ewing and Press, 1954; Jordan, 2020).1951年,该仪器被安装在美国拉蒙特,并在1952年11月4日记录到了Kamchatka半岛9级地震所产生的异常面波信号(最长周期可达480 s)(Ewing and Press, 1954).仪器的研制者Frank Press和Maurice Ewing基于这些面波信号获取了频散曲线,开创性地揭示了地球地幔的弹性结构(Ewing and Press, 1954).随后的 1950、1960年代,研究者们在美洲、非洲与太平洋等全球不同的区域开展了一系列的研究,通过提取的面波频散曲线认识到上地幔的不均匀性结构(如, Dorman et al., 1960; Ewing and Press, 1954; Kuo et al., 1962;McEvilly, 1964; Oliver and Ewing, 1957; Press et al.,1956; Takeuchi et al., 1959).如,Dorman 等(1960)基于中长周期瑞利波的频散曲线特征发现了大陆与大洋的上地幔均存在着一层低速层,这一研究成果是刚性板块位于低速层(软流圈)之上运动的重要地震学证据,支持了板块构造理论的发展.但是需要指出的是,早期的研究获取的是地震台站与地震事件间的平均频散,揭示的是台站与事件间面波传播路径的一维上地幔结构,并没有系统地开展三维层析成像研究.紧跟着Aki和Lee(1976)开创性的体波层析成像工作以及地震台网的加密,1980年代,面波层析成像方法也迅速发展.在这一时期,研究者们基于地震台网记录的面波频散信息开展了反演研究,构建了台网覆盖区域尺度与全球尺度上地幔的三维地震波速度(如, Anderson, 1987; Montagner, 1985; Nakanishi and Anderson, 1982, 1983,1984; Woodhouse and Dziewonski, 1984)、方位各向异性(如,Tanimoto and Anderson, 1984, 1985)与径向各向异性结构(如, Nataf et al., 1984,1986).虽然这些大尺度模型的构建是基于稀疏的宽频带地震仪,分辨率较低,但是其在认识板块尺度的上地幔横向不均匀性与不同构造背景的地球动力学过程等方面发挥了很重要的作用.
最近30年,面波层析成像方法已成为一种构建壳幔速度与各向异性结构的常规方法.另外,随着地震台网的加密(如,美国USArray计划与中国的喜马拉雅计划ChinArray等)和地震仪器的改进与创新,研究者们发展和完善了多种层析成像方法(如,双台法、双平面波法、程函方程法、Helmholtz方程法、背景噪声成像法等)来获取瑞利波与勒夫波的相速度和/或群速度(如, Forsyth and Li, 2005; Jin, 2015; Li and Li, 2015; Lin et al.,2008; Shapiro et al., 2005; Yao et al., 2005, 2006),构建了全球尺度、区域尺度与局部地区的壳幔速度与各向异性结构模型,提升了人类对于地球内部结构、动力学过程、地震灾害与矿产资源勘探等方面的深化认识.需要提到的是,这些方法都存在着一定的假设条件;另外,不同方法对地震事件分布与地震台网布设等有不同的要求.详细对比不同方法获取的相/群速度结果对融合各种方法开展S波速度与各向异性反演,进而分析壳幔介质的物理参数具有重要意义.虽然部分研究对比了背景噪声成像法与双平面波法(如, Li and Fu, 2020; Liu et al.,2021)、背景噪声成像法与双台法(如, Yao et al.,2006)等,然而现有研究对于多种不同方法获取的瑞利波与勒夫波相速度和/或群速度的可对比性尚未有一个系统的认识,为多种层析成像方法融合反演壳幔结构引入不确定性.
本文重点综述了多种常用的面波层析成像方法(双台法、双平面波法、程函方程法、Helmholtz方程法、背景噪声成像方法与直接面波层析成像法)的原理及其优缺点,并以青藏高原中部与北部、东北缘与东南缘为切入区域,基于这些区域已有的多种面波成像方法研究结果,详细对比了多种方法获取的瑞利波和/或勒夫波相速度.该研究能为不同面波层析成像方法获取的面波相速度和/或群速度融合以构建壳幔地震波速度与各向异性结构提供基础.本文侧重常规的面波层析成像方法的介绍及其在青藏高原的应用结果的对比,读者如想了解更多关于地震层析成像的历史及相关内容,可参考Nolet(2008)的专著、Rawlinson和 Sambrdge( 2003)、 Romanowicz( 2003)、 Rawlinson等(2010)及Liu和Gu(2012)等综述性文章.
1 面波层析成像方法
1.1 双台法
早在1960年代,研究者们开始利用单台法求得地震台站与震源间的平均面波频散曲线(如,Brune et al., 1960; Kuo et al., 1962),但是由于当时地震台站分布较为稀疏,这些研究仅能揭示大尺度的上地幔平均速度结构.另外,单台法往往会受到震源效应与地震波散射等因素的影响,其获取的群速度误差较大.为了消除震源带来的误差(如,震源位置的不准确性、发震时刻的不确定性与断层破裂过程等),双台法被提出来(McEvilly, 1964;Nafe and Brune, 1960; Satô, 1958)以获取面波的群速度和/或相速度.该方法要求震源与两个台站近似地位于同一个大圆弧路径上(图1a),基于窄带滤波获取不同频率的面波波形,对比两个台站的波形获取两个台站间的频散曲线(相速度/群速度).该方法可被延伸至使用多个地震台站,称为多台法(如, Knopoff et al., 1966).对于台站覆盖程度较低、但是震级大于5.5的地震较为频繁的区域,该方法可使用两个地震事件在单个台站的波形记录来获取该区域的频散信息,称为双地震事件方法(如,Romanowicz, 1982).
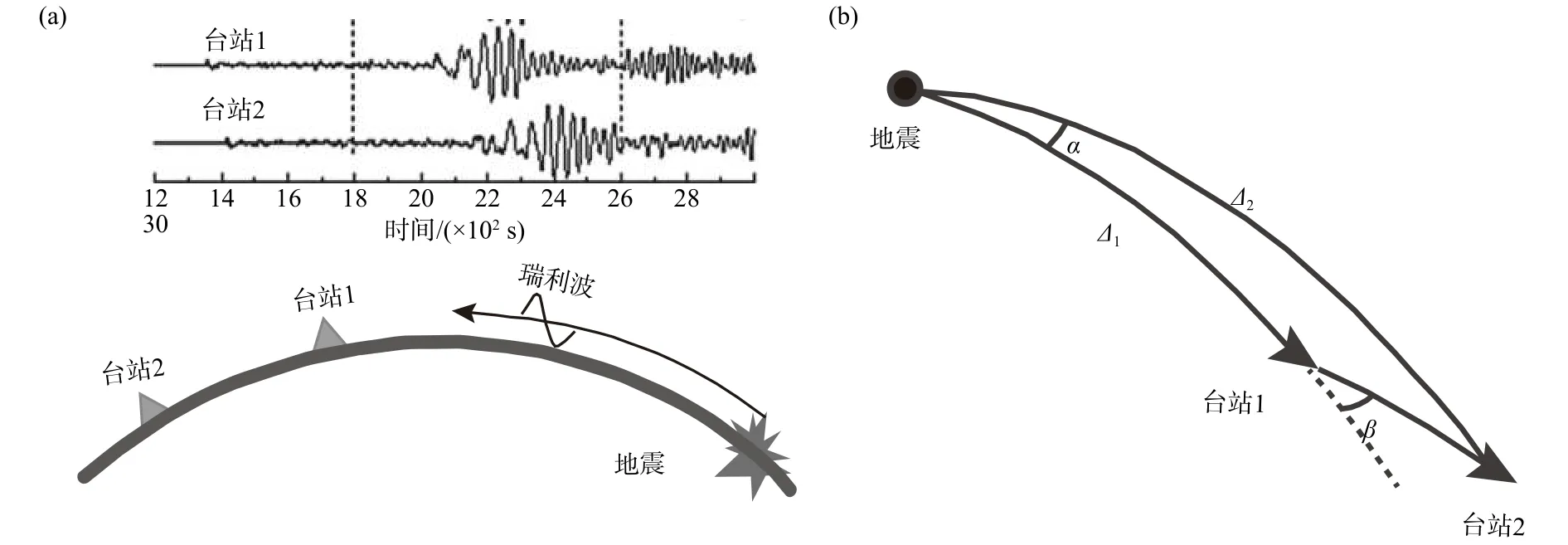
图1 (a)双台法的示意图,该方法假设震源与两个台站近似地位于同一个大圆弧路径上,两个台站的面波记录来源于Li和Li(2015);(b)双台法要求地震事件到近台的方位角与近台到远台的方位角之差β 小于3°(修改自Yao et al.,2006)Fig.1 (a) Schematic diagram for two-station method.This method assumes that the earthquake and two seismic stations are at same great circle.The two stations' surface waveforms are from Li and Li (2015).(b) The two-station method requires the difference of azimuthal angle β between the earthquake and two seismic stations is less than 3° (modified from Yao et al., 2006)
自Satô(1955, 1958)提出双台法以来,该方法被广泛应用于提取面波的群速度和/或相速度(Bourjot and Romanowicz, 1992; Brandon and Romanowicz, 1986; Curtis and Woodhouse, 1997;Knopoff, 1972; Kovach, 1978; McEvilly, 1964; Meier et al., 2004; Romanowicz, 1982; Wu et al., 2009; Yao et al., 2005, 2006).在最近20多年,研究者们针对双台法的方法改进、可视化以及面波层析成像反演方法改进等方面开展了广泛的研究.如,Meier等(2004)对两个台站记录的面波波形求互相关函数,并通过频率域的高斯滤波剔除噪声与高阶面波对频散的影响,提高了获取的基阶面波频散曲线的准确性;Yao等(2005, 2006)将双台法的数据处理与相速度提取流程进一步的融合与可视化.Wu等(2009)通过频率域小波变换频时分析,可同时获取单台群速度(基于多重滤波技术)与双台相速度.这些改进使得双台法更容易被研究者们所使用.另外,随着地震台站分布越来越密集,双台法已成为一种很常用的获取地震台阵覆盖区不同周期群速度和/或相速度图的面波层析成像方法.
双台法的基本步骤是首先基于窄带滤波获取不同频率的面波波形,然后基于这些波形进行互相关计算,进而对比两个地震台站的相位(时间域或频率域),获取台站间的频散.随后,以台站间的频散曲线作为输入,将台站覆盖区域参数化,开展层析成像反演计算,获取台站覆盖区不同周期的相速度分布图.
当运用双台法提取相速度和/或群速度频散曲线时,地震事件需满足如下的条件(Yao et al.,2005, 2006):(1)远震震中距需大于20°以避免近源效应的影响,需小于120°以避免高阶面波的干扰,地震震级最好大于5.5级以保证能获取信噪比较高的面波记录;(2)两个台站与地震震中大致在同一条大圆弧上,地震事件到近台的方位角与近台到远台的方位角之差β
需小于 3° (图1b)(Yao et al., 2006);(3)两个台站间的距离需大于80 km以保证获取的短周期面波信号可靠性.一般而言,对于某些台站数量较少的流动地震台网,满足上述条件的地震事件较少,使得射线密度较小,造成双台法获取的相速度图水平分辨率较低.1.2 双平面波层析成像法
地震面波在传播过程中当遇到地球的不均质异常时会偏离大圆弧路径,从而导致面波的多路径传播与散射(可称为非平面波能量)(如,Evernden,1953; Laske, 1995),进而影响面波波形的振幅和相位(Friederich and Wielandt, 1995).传统的地震台阵分析方法(如,双台法)会假设入射波场为平面波,忽略了非平面波能量(对于周期小于50 s的面波,其能量尤其大),从而引起相速度测量的系统偏差(Forsyth and Li, 2005).Forsyth等(1998)首次提出双平面波干涉面波层析成像方法(本文简称双平面波法),可用两个平面波干涉所形成的波场来代表入射波场(其中一个平面波可代表为非平面波能量),从而能较好克服由非平面波场能量对频散结果带来的影响(Forsyth and Li, 2005; Li and Li, 2015)(图2a).该方法首次被应用于东太平洋洋中脊区域,其获取的瑞利波相速度揭示了东太平洋洋中脊下方部分熔融体的分布范围较大(Forsyth et al., 1998).Forsyth和Li(2005)详细阐明了双平面波法的原理与数学推导,并指出该方法可同时获取瑞利波的相速度与方位各向异性.Yang和Forsyth(2006)将有限频理论(Zhou et al., 2004,2006)融合到双平面波法中,更好地校正了因散射导致的面波振幅与相位变化,进一步提高了面波相速度测量的可靠性,这对于长周期面波的改进尤为明显(Li, 2011).Li和Li(2015)进一步将该方法扩展至勒夫波,指出瑞利波与勒夫波结合可同时反演地震波速度与径向各向异性,对理解岩石圈的变形与地幔物质流动具有重要意义.

图2 (a)双平面波法示意图;(b)双平面波法的坐标系统设置(Forsyth and Li, 2005),三角形代表参考台站,而圆形代表任意台站;(c)局部笛卡尔坐标系统设置,零点(0, 0)为参考台站位置(修改自Li and Li, 2015)Fig.2 (a) Schematic diagram for two-plane-wave surface wave tomography.(b) The coordinate system setting used in two-planewave method (Forsyth and Li, 2005).The triangle denotes the seismic stations and circles represents the grid nodes;(c) Localized Cartesian coordinate system setting.Point (0, 0) is assigned as reference seismic station position (modified from Li and Li, 2015)
最近20年,双平面波法被广泛应用于获取地壳与上地幔的S波速度与各向异性结构(如, Cai et al., 2018; Chen and Li, 2012; Dave and Li, 2016; Forsyth et al., 1998; Fu et al., 2010, 2016, 2019; Li and Detrick, 2003; Li et al., 2003, 2005; Li, 2011; Li L et al.,2013, 2016, 2020; Li Y et al., 2013; Li and Li, 2015;Li and Fu, 2020; Liang et al., 2020; Liu et al., 2021;Miller et al., 2009; Rau and Forsyth, 2011; Schutt et al., 2008; Weeraratne et al., 2003, 2007; Yang and Forsyth, 2006; Yang et al., 2008; Zhang et al., 2011),揭示了全球不同区域(如,全球克拉通地区、大洋俯冲带地区、洋中脊、大陆造山带与大火成岩省等)的岩石圈结构、变形及相关动力学过程.
双平面波法假设入射波场由两个不同角度入射水平传播的平面波叠加形成(Forsyth and Li,2005).对于任一地震事件,在频率ω
下,瑞利波波场垂向上的位移可表达为:
k
与k
分别是两个平面波水平波数,x
是位置矢量.该方法针对每个地震事件依据震中与参考台站的位置设定局部的笛卡尔坐标体系;其中参考台站为坐标的原点,+x
坐标轴设定为震中与参考台站间的大圆弧方向,+y
坐标轴设定为x
方向顺时针旋转90.某点的x
坐标定义为震中到参考台站与震中到该点的距离差;某点的y
坐标定义为该点到+x
坐标抽的垂直距离(如图2b)(Forsyth and Li, 2005).地震台网记录的面波振幅最大的台站设为参考台站.笛卡尔坐标体系可变换至以参考台站为中心的极坐标体系 (r
,ψ).在极坐标体系 (r
,ψ)下,给定某个地震事件i
,在频率 ω下第k
个台站记录的总位移U
可描述为: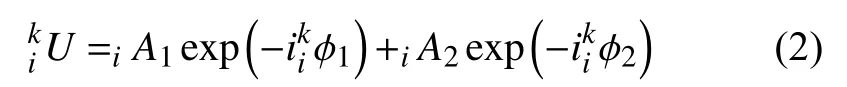

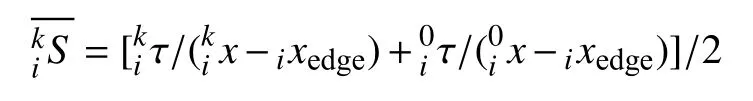


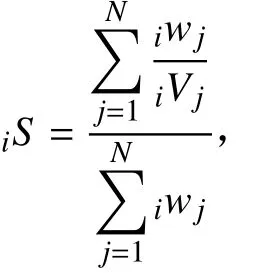
从以上的双平面波的正演数学推导可知,只用六个参数(两个平面波的振幅、参考相位、双平面波偏离大圆路径的角度)就可描述每个频率的地震波入射波场.在反演过程中,这些参数先用模拟退火方法估计,随后利用广义非线性反演算法同时求解更新这六个参数与网格点的相速度(Forsyth and Li, 2005).
Li和Li(2015)进一步将双平面波法扩展至勒夫波中.对于瑞利波,反演过程中只用到地震仪的垂直分量,两个平面波的振幅可以直接相加.而勒夫波的质点运动只发生在地震仪的切向分量,并且垂直于大圆弧方向,在参考台站与其他台站会稍有不同.所以,勒夫波质点位移需分解为x
与y
两个分量(如图2c).地震台站记录的勒夫波x
和y
分量的振幅可近似表示为Ax = A
sin(dϕ
) 和Ay =A
cos(dϕ
),其中A
为台站切向分量的勒夫波波形的振幅,dϕ
为给定台站和参考台站之间的方位角差;双平面波的勒夫波振幅可分解为x
和y
分量的振幅,表达为:
A
和A
分别代表每个平面波的振幅;θ
和θ
分别代表每个平面波的射线到x
坐标轴以及大圆弧到参考台站间的夹角.Ay
始终为正,而Ax
可为正或负;Ay
远大于Ax
的绝对值.勒夫波在ω
频率的入射波场可用x
和y
分量上的两个平面波来表示.相位、走时和慢度的计算以及反演问题的设置与瑞利波的相同.勒夫波双平面波法只是在观测和预测数据中添加了一个分量,最终的位移是x
与y
分量的总和.双平面波法对地震事件分布的要求较为简单,地震事件需满足震级大于5.5级,震中距位于25与120之间以消除近源效应与高阶面波的干扰.因此,双平面波法对于台站覆盖较差的区域(对于每个地震事件地震台站数仅需大于6个)也可以反演相速度图像.另外,与双台法相比,其射线密度较高,获取的相速度图像水平分辨率较高.
1.3 基于程函方程与Helmholtz方程的面波层析成像方法
如1.2节所述,地球的不均质性会造成地震波传播过程中偏离大圆弧路径,除了双平面波法外,基于程函方程的面波层析成像方法(本文称程函方程法)也能够部分减少非平面波场能量对相速度的影响.Lin等(2009)提出了一种高频近似条件下基于程函方程的面波层析成像方法,该方法假设波形的振幅是逐渐变化的,基于程函方程可计算面波的相位走时场梯度,进而可估算某一频率下局部区域的相速度的大小与方向(Lin et al., 2009).Lin等(2009)基于背景噪声互相关数据,将该方法应用至美国西部地区,获取了水平分辨率较高的相速度分布图.
假设忽略高阶面波与散射的影响,面波的到时可用以下的公式计算:

r
和r
是震源与台站的位置,r
是研究区中的任意点,m
=1或者2(分别代表线积分与面积分).对于射线理论,取m
=1,并且A
(r
,r
,r
)只在地震波传播(或者几何射线)的射线上有值,即假设地震射线是高频近似.而m
=2时,假设地震射线为有限频率.由上式可知,地震波的走时受局部介质相速度的影响.如果已知任意点r
相对于震源位置r
的走时场信息,我们则可以获取局部介质的相速度,即可用程函方程表达为: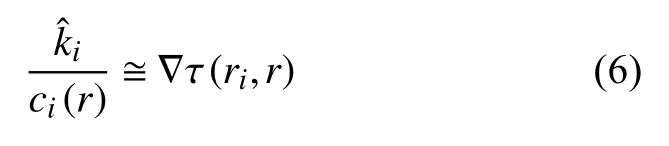

由上述的公式推导可知基于程函方程法大致可为两个步骤:(1)波场面追踪,即以某个台站(或地震事件)为中心,计算台站间的相延迟(到时);(2)基于程函方程利用插值方法计算研究区每个网格点的相同到时面的梯度;其中,梯度的大小代表局部慢度(即相速度)大小,而梯度的方向为几何射线的传播方向,进而构建整个区域的相速度分布(Lin et al., 2009).
需要提到的是,程函方程法忽略了振幅的信息,在速度异常体小于波长与多路径传播现象出现的情况下,可能会引起相速度测量系统的误差.Lin和Ritzwoller(2011)基于Helmholtz方程进一步地校正了振幅对相速度与方位各向异性的影响,通过应用于地震面波,该工作发现基于Helmholtz方程的层析成像方法(本文称Helmholtz方程法)获取的地震面波相速度与方位各向异性信息(尤其是对于周期大于50 s的面波)比基于程函方程的方法要可靠.Jin(2015)发展了一个多通道互相关的面波相速度自动测量系统(ASWMS),分别基于程函方程和Helmholtz方程面波层析成像法获取了美国大陆周期为20~100 s瑞利波的相速度图.通过对比程函方程法和Helmholtz方程法获取的结果,认为Helmholtz方程法获取的相速度图像更为可靠.
另外,基于程函方程和Helmholtz方程的面波层析成像方法可直接从地震记录计算同时获取面波相速度与方位各向异性,不需要经过正演与反演的过程,可以避免在反演过程中模型平滑与阻尼等参数设置所引起的不确定性.而且,该方法易于估算相速度的误差与水平分辨率(主要与台站间距相关),并且计算较为方便,快速.但是,该方法要求台站分布规则并且密度较高,不太适用于台站间距较大与台站较为稀疏的研究区域.
1.4 背景噪声面波层析成像法
上述三种方法被广泛应用于天然地震所产生的面波信号,天然地震事件产生的面波周期较长(通常大于15 s),能够很好地揭示地球上地幔的深部结构,但是对于浅部地壳的约束较弱.Lobkis和Weaver(2001)提出对两个地震台站的背景噪声进行互相关计算,对互相关信号求时间的导数可提取出包含有面波信息的台站间经验格林函数,而两个台站中的任一台站可以看作为一个虚震源.Shapiro等(2005)首次将方法(背景噪声层析成像法,简称背景噪声法)应用于获取美国加州地区的地壳速度结构,其对比了背景噪声互相关计算获取的面波信号与地震面波信号,两者存在着高度的一致性,佐证了背景噪声互相关提取面波格林函数的可靠性.通常来说,背景噪声法能够获取周期较短的面波的信号(4~40 s),能够很好地约束地壳内部的结构.最近20年,背景噪声层析成像已经被广泛应用于全球各个区域,现在已成为获取地壳内部结构的一种常用的方法.另外,研究者们还利用背景噪声互相关的方法提取体波信号(如, Poli et al., 2012,2015; Riahi et al., 2021; Shirzad and Shomali, 2016)与长周期面波信号(50~250 s, Xie et al., 2016),应用于探测深部地幔与地核的结构,该文重点关注短周期面波信号,对该方面内容不做展开.
背景噪声层析成像方法的基本步骤是:(1)通过对两个台站记录的长时间序列的连续波形进行互相关,得到台站对之间的经验格林函数:(2)对经验格林函数(面波信号)作频率—波数分析即可获取面波的频散曲线,随后通过层析成像反演计算可构建研究区域的二维群速度/相速度结构;或者对经验格林函数直接开展基于程函方程的层析成像研究,可直接获取研究区的二维群速度/相速度结构.
与地震面波层析成像方法相比,背景噪声层析成像方法主要的优点是无需震源就可获取高分辨率地壳尺度的成像结果(Shapiro et al., 2005).因为其不依赖于地震的震源,所以该方法能够有效地消除因震源参数(地震定位、发震时刻等)不确定性带来的误差.另外,背景噪声层析成像方法的水平分辨率主要取决于台站的间距与面波的波长,并不依赖于台站和地震之间射线分布情况,因而在有足够多地震台站的研究区域,能够获取水平分辨率较高的速度图像.需要指出的是,背景噪声层析成像通常需通过较长的观测时间来确保获取的面波信号有足够高的信噪比,要求台站的布设时间足够长.另外,针对区域地震台网基于背景噪声提取的频散最长周期一般为40 s,只能较好地约束地球浅部结构(通常为地壳部分),通常需要结合远震面波层析成像方法获取的长周期面波频散数据才可通过S波速度反演约束地球的壳幔结构.对于地震仪记录的信号在水平分量较垂直分量而言,更易受局部性干扰源的影响,其信噪比要低,使得背景噪声层析成像通常仅能获取瑞利波的频散信息,利用勒夫波进行噪声层析成像的研究较少.对于背景噪声层析成像,前人作了详细的综述,本文对其详细原理与发展历程,不作总结阐述,关于背景噪声数据处理、具体原理与发展历史等相关内容读者可参考Shapiro和 Campillo(2004)、Shapiro等(2005)、Larose等 ( 2006)、 Bensen等 ( 2007)、 Gouedard等(2008)、Ritzwoller等(2011)以及徐义贤和罗银河(2015)等文章.
1.5 直接面波层析成像法
上文介绍的双台法、双平面波法、程函方程法、Helmholtz方程法和背景噪声成像法几种常用面波层析成像方法可用于构建研究区的相速度(或群速度)分布图,随后还需要开展最小二乘法反演(如, Li et al., 2005)、近邻算法(如, Yao et al.,2008)或蒙特卡洛反演方法(如, Shen et al., 2016)获取S波速度和方位各向异性结构.这种传统的两步法通常是针对研究区的单个网格点开展反演,随后通过汇集所有网格点构建研究区的三维结构.Fang等(2015)提出一种直接反演三维S波速度结构的方法(本文称直接面波层析成像方法),该方法考虑了地震面波在复杂介质中非大圆弧路径传播的影响,利用快速行进算法对每个周期面波的二维相速度图进行射线追踪(Rawlinson and Sambridge, 2003),整合每个频率面波的深度敏感核函数,通过最小二乘法迭代更新三维速度模型,直接将台站间的频散数据反演获取三维S波速度结构.与传统的两步法相比,减少了中间反演二维相速度/群速度图像的步骤,且能充分利用所有周期的相速度和/或群速度信息(Fang et al., 2015).该方法考虑了短周期面波的非大圆弧路径传播的影响,对于短周期面波获得的S波速度结构更为可靠.然而,由于该方法属于线性化的反演,需要设置合理的初始模型,以避免陷入局部极值.
基于初始三维P波与S波速度、密度模型,可正演获取台站间不同频率的面波理论走时,在频率ω的路径i
的观测和理论走时残差可表示为:
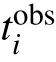
C
(ω)可通过对三个参数的偏导数积分获得:
该方法使用一种简单的差分方法来计算在给定深度下相/群速度相对于每个参数(即 α、 β、 ρ)的灵敏度(Fang et al., 2015).由于面波对S波速度最为敏感,计算P波速度与密度时可使用经验关系将S波速度与密度和纵波速度联系起来(Brocher,2005).联立(7)与(8)可得:
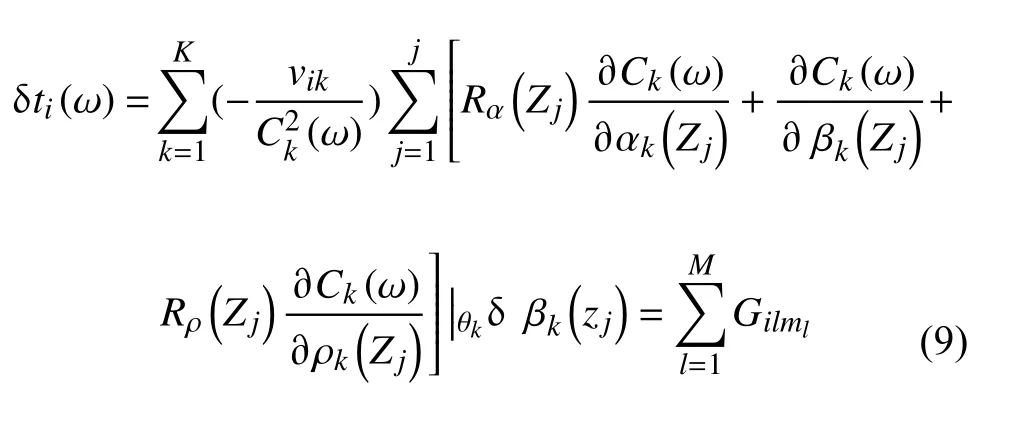
K
、J
分别为参数化模型的水平、垂直格点个数.因此,M
=KJ
为三维模型的总网格节点.可以将上述公式转化为矩阵形式:
d
是所有路径与频率的到时残差矩阵,G
是数据敏感核矩阵,m
是模型.G
可由初始模型计算获取,并在每次迭代过程中更新.随后,通过最小二乘法获取研究区的三维S波速度模型.可参考Fang等(2015)获取详细的反演流程,本文不作论述.Liu等(2019)将此方法继续拓展,可同时获取S波速度与方位各向异性.该拓展方法的优点是直接考虑了S波速度结构的三维不均匀性与各向异性的权衡(trade-off),改善了传统两步法因各向异性假设所引入的误差.此外,Zhang等(2018)进一步发展了基于蒙特卡洛的面波直接反演方法,可去除对初始模型的依赖以及获得模型的不确定度,但由于计算量还相对较大,非线性面波直接反演方法目前只被应用在少数区域.关于直接面波层析成像的具体原理等相关内容,读者可参考Fang等(2015)与Liu等(2019).
2 青藏高原的面波层析成像研究及不同面波层析成像方法的应用与对比
2.1 青藏高原面波层析成像研究的简要历史与现状
1980年代前,布设在青藏高原的宽频带地震台站十分稀疏,基于面波层析成像揭示青藏高原造山带深部结构的研究较为稀少.1980年代与1990年代初期,基于全球标准地震台网(WWSSN)与中法合作布设的零星宽频带地震台站等所记录的地震面波数据,研究者们开展了大尺度低分辨率的面波层析成像研究(如, Bourjot and Romanowics,1992; Brandon and Romanowics, 1986; Chen et al.,1993; Feng and Teng, 1983; Jobert et al., 1985;Romanowicz, 1982; Wu and Levshin, 1994),如,Romanowicz(1982)基于双台法的双地震事件方法初步获取了青藏高原地区的30~90 s瑞利波与勒夫波相速度频散,发现了青藏高原的上地幔100~150 km深度存在一个低速区.
1990年代至今,在国际合作、地区合作与中国国家地震台网等计划的驱动下,在青藏高原地区布设了大量的宽频带流动与固定地震台站(滕吉文等,2019),如,中美合作计划(1991—1992)、历时 20多年的 INDEPTH计划(1992—2016)、HIMNT(2001—2002)、Hi-CLIMB(2002—2005)、Namcha Barwa(2003—2004)、MIT-China(2003—2004)、NETS(2008—2010)、SinoProbe(2008—2014)、喜马拉雅计划(ChinaArray, 2010—2015)、羚羊计划(ANTILOPE,2003至今,Zhao et al.,2021)、SANDWICH(2012—2016, Liang et al.,2016)以及其它流动台网等.图3展示了青藏高原区域中部与东部现有的部分宽频带地震台站分布(图3).研究者们基于这些流动地震台站所记录的地震面波与背景信号,针对青藏高原造山带的深部结构开展了广泛的双台法、双平面波法、程函方程法、Helmholtz方程、背景噪声法与直接面波层析成像法等研究(如, Agius and Lebedev, 2013; Bao et al., 2015, 2020; Ceylan et al., 2012; Chen et al.,2010; Deng et al., 2015; 范莉苹等, 2015; Feng et al.,2020; Fu et al., 2010, 2016, 2019; 付媛媛和肖卓,2020; Guo and Chen, 2017; 黄忠贤等, 2014; Jiang et al., 2011; Jiang et al., 2014; Legendr et al., 2015; Li H et al., 2009, 2010, 2014; Li J et al., 2017; Li L et al.,2013, 2016, 2020; Li M et al., 2016; Li X et al., 2014;Li Y et al., 2008, 2013, 2017; Li and Fu, 2020; Lü and Lei, 2018; Liang et al., 2020; Liu et al., 2014; Liu et al., 2019; 鲁来玉等, 2014; Nunn et al., 2014; 潘佳铁等, 2015; Pandey et al., 2015; Shen et al., 2016; 苏伟等, 2008; Sun et al., 2010; Wang and Gao, 2014; 王琼等, 2015; 王琼和高原, 2018; 王怀富等, 2020; Wang et al., 2020; Wei et al., 2017; Wu et al., 2016; Xie et al., 2013; Yang et al., 2010; Yao et al., 2005, 2006,2010; Zhang et al., 2011; 钟世军等, 2017; 朱子杰等,2021),如,Yao等(2006)结合背景噪声与双台法获取了青藏高原东南缘壳幔速度结构,约束了该地区的岩石圈变形特征;Yang等(2010, 2012)基于瑞利波背景噪声层析成像首次获取了青藏高原地壳尺度的水平分辨率较高的S波速度结构,揭示了高原地壳流的空间分布;Li和Fu(2020)基于双平面波层析成像方法构建了青藏高原中部与东部的瑞利波与勒夫波的长周期相速度图,并结合背景噪声获取的短周期面波相速度频散,进一步的获取了壳幔S波速度与径向各向异性结构(Li et al.,2021),很好地约束了这些区域的地壳的流变强度与印度岩石圈地幔的俯冲前沿.基于背景噪声成像,Bao等(2020)构建了青藏高原东部壳幔S速度与方位各向异性模型,并提出高原两阶段生长变形模式,即早期高原隆升受控于地壳不均匀增厚,而后期中下地壳物质发生不规则小尺度塑性流动,形成现在平坦的高原地貌.随着喜马拉雅计划一期和二期密集地震台站的布设,基于程函方程与Helmholtz方程的面波层析成像也被应用于获取青藏高原东北缘与东南缘的岩石圈S波速度与方位各向异性结构(如,王怀富等,2020;钟世军等,2017).这些面波层析成像研究的结果对于揭示青藏高原岩石圈的不均匀分布与地壳物质的强度,进而认识青藏高原的深部动力学与变形机制等问题提供了关键的约束.
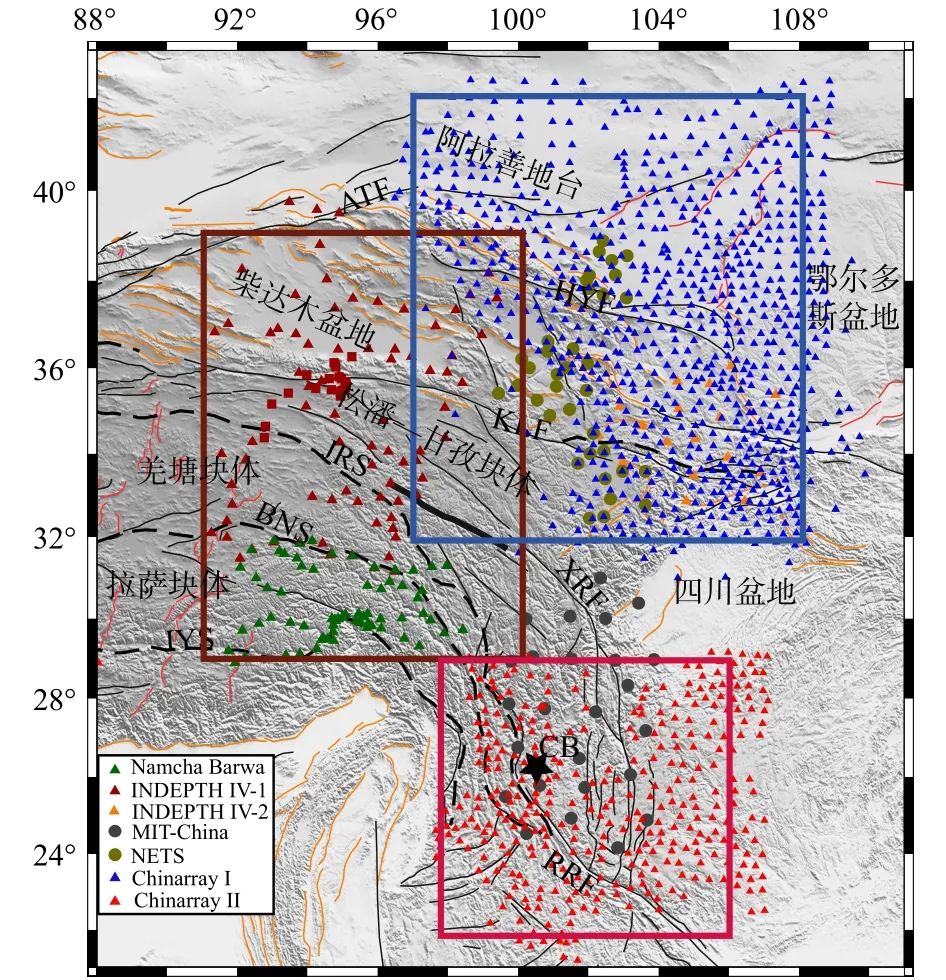
图3 青藏高原中部与东部的构造、地形与地震台站分布图.棕色方框代表青藏高原中北部(面波相速度对比范围);蓝色方框代表青藏高原东北缘(面波相速度对比范围);红色方框代表青藏高原东南缘(面波相速度对比范围);黑色五角星代表形成峨眉山大火成岩省的峨眉山地幔柱的中心位置.CB:川滇块体;IYS:印支— 雅鲁藏布缝合带;BNS:班公—怒江缝合带;JRS:金沙江缝合带;KLF:昆仑断裂;HYF:海原断裂;ATF:阿尔金断裂;XRF:鲜水河断裂Fig.3 The tectonic and topographic map of the central-eastern Tibetan Plateau with seismic stations distribution.Brown box represents the region of central-northern Tibet for the comparison of phase velocity maps; The blue and red boxes denote the northeastern and southeastern Tibet, respectively; The black star denotes the center of the Emeishan mantle plume that was suggest to produce the Emeishan large igneous province.CB: the Chuandian Block; IYS: Indus-Yarlung suture zone;BNS: Bangong-Nujiang suture zone; JRS: Jinsha River suture zone; KLF: Kunlun fault; HYF: Haiyuan Fault;ATF: Altyn Tagh Fault.XRF: Xianshui River Fault
2.2 各种地震面波层析成像方法在青藏高原的应用及对比
不同的面波层析成像方法各有优缺点,加强不同方法的对比研究有助于确定青藏高原壳幔速度结构与各向异性结构的主要可靠特征;而不同方法的对比最好是基于同一数据集.基于这一原则,我们基于INDEPHTH IV、NETS和MIT-China与喜马拉雅计划(一期和二期)等台网的流动地震台站记录的地震面波与背景噪声数据,在青藏高原中部与北部地区对比了背景噪声与双平面法,在青藏高原东北缘地区对比了双台法、程函方程法与背景噪声法,在青藏高原东南缘地区对比了双台法、双平面法、程函方程法、背景噪声法与直接面波层析成像法.
2.2.1 背景噪声与双平面法在青藏高原中部与北部的对比
Xie等(2013)基于 INDEPHTH IV、NETS和MIT-China等地震台网记录的数据利用背景噪声层析成像方法获取了青藏高原中部与东部的瑞利波与勒夫波的相速度图(周期为5~40 s);Li和Fu(2020)基于相似的地震台网利用双平面波层析成像方法构建了青藏高原中部与东部的瑞利波与勒夫波的长周期相速度图(周期范围为20~143 s).需要指出的,目前在青藏高原中部主要为流动宽频带地震台网,台站间距较大,难以在该地区开展基于程函方程与程函方程的面波层析成像方法研究,因此在青藏高原中部与北部,我们只对比了背景噪声成像法与双平面波法获取的瑞利波与勒夫波相速度图.
从图4与图5可看出,双平面波法与背景噪声成像法获取的相速度图的空间展布高度吻合,主要表现为:在短中周期的瑞利波(20 s、30 s、40 s与50 s)与勒夫波(20 s、30 s与40 s)相速度图中(对地壳有很好的约束),羌塘块体与松潘—甘孜块体的东北部都表现为低速度特征,而羌塘块体的速度尤为低.而柴达木盆地区域表现为相对高速.这些速度特征反映了羌塘块体与松潘—甘孜块体东北部区域的地壳物质强度较柴达木盆地要强,更易于变形.需要注意的是,双平面波法获取的勒夫波相速度图展示出较强的不均匀性,尤其是在20 s周期(图5),这可能是因为地震所产生的勒夫波易受高阶面波与其他震相干扰,造成双平面波法获取的勒夫波相速度存在系统偏差.总体而言,两种方法获取的相速度绝对值之差大部分都在0.1 km/s之内,这印证了两种方法的可靠性,两者融合可构建壳幔速度结构.特别需要提到的是,双平面波除了获取短中周期的相速度图以外,还能获取长周期的相速度图(67 s、90 s、100 s与125 s,图6),融合背景噪声成像法获取的更短周期(6~20 s)相速度图,可同时构建壳幔速度与各向异性结构(Li et al., 2021),对揭示岩石圈的结构(甚至软流圈)与变形,从而认识大陆动力学过程具有重要作用.

图4 青藏高原中部与北部双平面法和背景噪声成像获取的瑞利波相速度图像对比.(a-d)双平面波法获取的相速度图像(20 s、30 s、40 s和50 s周期)(数据来自于Li and Fu, 2020);(e-h)背景噪声成像获取的相速度图像(20 s、30 s、40 s和50 s周期)(数据来自于Xie et al., 2013);(i-l)两种方法在相对应的周期获取的相速度图像之差值.TPW代表双平面波法.ANT代表背景噪声层析成像.左下方的数据代表相速度图像的周期与用于计算速度扰动的平均值Fig.4 The comparisons of Rayleigh-wave phase velocity maps obtained from two-plane-wave method and ambient noise tomography in the central-northern Tibetan Plateau.(a-d) Phase velocity maps at periods of 20 s, 30 s, 40 s and 50 s obtained from twoplane-wave method (data from Li and Fu, 2020); (e-h) Phase velocity maps at periods of 20 s, 30 s, 40 s and 50 s obtained from ambient noise tomography (data from Xie et al, 2013).(i-l) The differences of phase velocities obtained from two methods.TPW represents the two-plane-wave method.ANT denotes ambient noise tomography.The number in the left corner denotes the average phase velocity value used to calculate the velocity perturbations

图5 青藏高原中部与北部双平面法和背景噪声成像获取的勒夫波相速度图像对比.(a-c)双平面波法获取的相速度图像(20 s、30 s和40 s周期)(数据来自于Li and Fu, 2020);(d-f)背景噪声成像获取的相速度图像(20 s、30 s和40 s周期)(数据来自于Xie et al., 2013);(g-i)两种方法在相对应的周期获取的相速度图像之差值Fig.5 The comparisons of Love-wave phase velocity maps obtained from two-plane-wave method and ambient noise tomography in the central-northern Tibetan Plateau.(a-c) Phase velocity maps at periods of 20 s, 30 s and 40 s obtained from two-plane-wave method (data from Li and Fu, 2020); (d-f) Phase velocity maps at periods of 20 s, 30 s and 40 s obtained from ambient noise tomography (data from Xie et al, 2013).(g-i) The differences of phase velocities obtained from two methods

图6 青藏高原中部与北部双平面法获取的瑞利波与勒夫波长周期(67 s、90 s、100 s和125s)相速度图像(数据来自于Li and Fu, 2020)Fig.6 Rayleigh-wave and Love-wave phase velocity maps at periods of 67 s, 90 s, 100 s and 125 s obtained from two-plane-wave method in the central-northern Tibet (data from Li and Fu, 2020)
在昆仑断裂以北的柴达木盆地,双平面波法与背景噪声成像法获取的相速度图都表现为相对高速特征,但是双平面波法获取的高速体强度比背景噪声成像法要大,这可能是反演过程中两种方法射线覆盖率与反演参数(如,平滑参数)等有所差异所造成.
2.2.2 双台法、程函方程法与背景噪声成像法在青藏高原东北缘的对比
喜马拉雅计划二期在青藏高原东北缘布设了670套宽频带流动地震台站,平均台站间距为35 km.Li J等(2017)利用双台法构建了该区域周期为20~150 s的瑞利波相速度图.钟世军等(2017)基于这些台网记录的面波记录,开展了基于程函方程的面波层析成像研究,获取了青藏高原东北缘周期为12~60 s的瑞利波相速度图.因此,在青藏高原东北缘,我们详细对比了双台法与基于程函方程法获取的瑞利波相速度.另外,Shen等(2016)基于喜马拉雅二期以外的其他宽频带地震台站获取了整个青藏高原区域的相速度,因为该背景噪声成像法研究获取了20~40 s周期的相速度,所以对比背景噪声方法时选用了该研究的相速度图结果.
从图7可看出,背景噪声成像、双台法与程函方程法在同一周期(20 s、32 s和40 s)获取的相速度图的主要相对速度特征高度相似,并且获取的绝对值速度也较为接近,主要表现为:在青藏高原的松潘—甘孜块体与祁连山区域表现为低速度特征,这反映了这两个区域中下地壳物质较为软弱、都易于变形;进一步结合该区域的较高的莫霍温度(Li et al., 2021),可能指示了祁连山与青藏高原东北缘中下地壳的物质发生了部分熔融,这可能暗示该区域存在局部上地幔热物质上涌(Deng et al., 2018;Fu et al., 2019; Li L et al., 2013, 2016; Li Y et al.,2017).另外,阿拉善地块与鄂尔多斯盆地的西部大体表现为相对的高速.在20 s与32 s的相速度图中(大致反映10~35 km深度的S波速度结构),鄂尔多斯盆地西北部的贺兰山—银川地堑表现为相对低速度特征.

图7 青藏高原东北缘双台法、程函方程法与背景噪声成像法获取的中短周期(20 s、32 s和40 s)瑞利波相速度图像对比.(a-c)背景噪声成像获取的相速度图像(20s、32 s和40 s)(数据来自于Shen et al., 2016);(d-f)双台法波获取的相速度图像(20 s、32 s和40 s)(数据来自于Li Y et al., 2017);(g-i)程函方程法获取的相速度图像(20 s、32 s和40 s)(修改自钟世军等,2017).蓝色虚线圈代表三种方法观测到青藏高原松潘—甘孜块体与祁连山地区的低速区的一致性特征.ANT代表背景噪声层析成像; TS:双台法;EE:基于程函方程法.在图7a中,GAP: 阿拉善地块; TP:青藏高原;QL:祁连山;H-Y:贺兰山—银川地堑Fig.7 The comparisons of Rayleigh-wave phase velocity maps at periods of 20 s, 32 s and 40 s obtained from two-station, Eikonal equation, and ambient noise tomography in the central-northern Tibetan Plateau.(a-c) Phase velocity maps at periods of 20 s,32 s and 40 s obtained from ambient noise tomography (data from Shen et al., 2016); (d-f) Phase velocity maps at periods of 20 s, 32 s and 40 s obtained from two-station (data from Li Y et al, 2017).(g-i) Phase velocity maps at periods of 20 s, 32 s and 40 s obtained from Eikonal equation method (modified from Zhong et al., 2017).Two blue dash circles denote the low velocity zone in the Songpan-Ganzi Terrane, and Qilian Orogenic belt that are consistent in the phase velocity maps three methods.ANT: Ambient noise tomography; TS: Two-station method; EE: Eikonal equation method.In Figure 7a, GAP: Gobi-Alashan Platform; TP: Tibetan Plateau; QL: Qilian Orogenic belt; H-Y: Helanshan-Yinchuan Graben
2.2.3 背景噪声法、双台法、双平面法、程函方程法与直接面波层析成像法在青藏高原东南缘的对比
喜马拉雅计划一期在青藏高原东南缘布设了320多套宽频带流动地震台站,平均台站间距为35 km.基于喜马拉雅一期台网与其他地方台网记录的地震与背景噪声数据,前人在青藏高原东南缘开展了大量的面波层析成像研究工作(如, Fu et al.,2016; Liu et al., 2014; Liu et al., 2019; Liu et al., 2021;王怀富等, 2020; Yao et al., 2006, 2010; Zhao et al.,2021; 朱子杰等, 2021).如,王怀富等(2020)基于这些台网记录的面波记录,基于程函方程的面波层析成像法获取青藏高原东南缘周期为14~80 s的瑞利相速度图及对应的方位各向异性图像.潘佳铁等(2015)基于连续小波变换的时频分析双台法获取了该区域10~60 s的相速度图.Fu等(2017)基于双平面波法获取了20~100 s的瑞利面波相速度图.Liu等(2019)基于直接面波层析成像法获取该区域的S波速度与方位各向异性结构.这些面波层析成像的研究为认识青藏高原东南缘的中下地壳物质流动的空间分布与地幔物质流动等特征,进而揭示该区域的地球动力学过程提供了重要的约束.在青藏高原东南缘,我们详细对比了双台法、双平面波法与程函方程法获取的短中周期(20 s与40 s)瑞利波相速度图.另外,我们还与背景噪声成像法获取的相速度图(Shen et al., 2016)作了对比.
四种方法(背景噪声法、双台法、双平面法与程函方程法)在相同或者相近周期的相速度图像(20 s与40 s周期附近,主要反映15~50 km深度范围的地壳S波速度结构)呈现出比较相似的特征(图8),主要表现为:在青藏高原以低速度特征为主,往南低速体似乎分为两个分支,一个低速区位于红河断裂附近,另外一个低速区位于鲜水河断裂附近.川滇块体(峨眉山大火成岩省的内带)主要以相对高速为主.这些相速度图变化特征与直接面波层析成像获取的不同深部S波速度结构高度吻合(图9,Liu et al., 2019).低速度特征反映了青藏高原中下地壳物质向南流动的方向与几何形态.受峨眉山地幔柱的影响,固结的岩浆分布在川滇块体的地壳,强化了该区域的物质强度,从而阻挡青藏高原地壳流的大规模向南扩展,使得地壳流局限于沿着地壳薄弱区(即红河断裂带与鲜水河断裂带)向南逃逸(Li et al., 2021; Liu et al., 2014; Liu et al.,2019; Liu et al., 2021).需要指出的是,王怀富等(2020)同时反演瑞利相速度与方位各向异性图像,其获取的瑞利相速度相对单一相速度反演较为平滑.

图8 青藏高原东南缘背景噪声成像法、双平面波法、双台法与程函方程法获取的短中周期(20 s和40 s)瑞利波相速度图像对比.(a-b)背景噪声成像获取的相速度图像(20 s和40 s)(数据来自于Shen et al., 2016);其中,黑色虚线代表峨眉山大火成岩省的内带和中带;(c-d)双平面波法波获取的相速度图像(20 s和40 s)(数据来自于Fu et al.,2017);(e-f)双台法波获取的相速度图像(20 s和40 s)(修改自潘佳铁等,2015);(g-h)程函方程法获取的相速度图像(20 s和36 s)(修改自王怀富等,2020).白色虚线圈代表两种方法观测到的一致性特征.ANT:背景噪声层析成像;TPW:双平面波法;TS:双台法;EE:程函方程法Fig.8 The comparisons of Rayleigh-wave phase velocity maps at periods of 20 s and 40 s obtained from ambient noise tomography,two-plane-wave method, two-station method, and Eikonal equation method in the southeastern Tibetan Plateau.(a-b) Phase velocity maps at periods of 20 s and 40 s obtained from ambient noise tomography (data from Shen et al., 2016); Black dashed line denoted the inner and intermediate zones of Emeishan large igneous province; (c-d) Phase velocity maps at periods of 20 s and 40 s obtained from two-plane-wave method (data from Fu et al., 2017).(e-f) Phase velocity maps at periods of 20 s and 40 s obtained from two-station method (modified from Pan et al., 2015).(g-h) Phase velocity maps at periods of 20 s and 36 s obtained from Eikonal equation method (modified from Wang et al., 2020).White dashed circle denotes the consistent features from multiple methods.ANT: Ambient noise tomography; TPW: Two-plane-wave method; TS: Two-station method; EE:Eikonal equation method

图9 直接面波层析成像法获取的地壳与上地幔顶部三维S波速度模型及方位各向异性(修改自Liu et al., 2019)Fig.9 Three-dimensional S wave velocity model and corresponding azimuthal anisotropy in the crust and uppermost mantle obtained from direct surface wave tomography (modified from Liu et al., 2019)
3 结论与展望
本文综述了面波层析成像的几种常见方法(双台法、双平面波法、程函方程法、Helmholtz方程法、背景噪声成像法与直接面波层析成像法)的基本原理及其优缺点,并对比了这几种方法在青藏高原中部与北部、东北缘与东南缘三个地区的应用,能为不同面波层析成像方法获取的速度联合解释,以构建壳幔地震波速度与各向异性结构提供基础.我们得到以下主要结论:
(1)多种面波层析成像方法获取的同一周期相速度图像相对速度特征高度吻合,受不同方法所采用的反演参数与射线覆盖程度差异等因素的影响,使得不同方法获取的绝对速度值有些小差别,但是在误差范围之内,这表明几种方法获取的相速度图像都较为可靠,具有可对比性,可融合几种方法获取的相速度频散开展S波速度与各向异性反演研究.
(2)多种面波层析成像方法获取的相速度图像都观测到较为相似的速度特征,主要表现为:在短中周期(20~40 s)青藏高原内部(尤以羌塘地体、松潘—甘孜块体东北部为明显)表现为低速度特征,在青藏高原东南缘低速体分为两个分支,沿着红河断裂与鲜水河断裂附近分布,这些低速度特征表明青藏高原内部的中下地壳的物质较为软弱,局部地区可能存在部分熔融体,在印度板块向北俯冲的作用下,高原内部的中下地壳物质沿断裂带附近发生流动;在青藏高原东南缘,受峨眉山大火成岩凝固岩浆所造成的强度较强的川滇块体的阻挡下,中下地壳流主要沿着薄弱带附近(即红河断裂带与鲜水河断裂带)向南逃逸.祁连山表现为低速度特征,可能反映该区域的地壳易于变形,结合该地区的较高的莫霍温度,推测低速可能与上地幔物质上涌相关.
新近发展起来的多阶面波成像法能很好地将高阶面波的信息加入到S波速度的反演中,进一步提高S波速度结构的垂直分辨率,并减少了反演的非唯一性(Wang et al., 2019).该方法通过频率—矢量波数域变换法(F-J方法)从两个地震台站的互相关信号中提取中高阶面波,基阶面波与高阶面波的频散结合能够精确地共同约束上地幔深部S波速度结构.此外,基于短周期密集地震台阵记录的噪声数据,通过背景噪声层析成像方法可获取高频面波频散信号,可构建浅地表高分辨率的速度结构,适用于探测浅地壳的断层(如, Zhang et al., 2020)、金属矿床区(如, Zheng et al., 2022)、人工诱发地震活动区(如, Dong et al., 2022)、强震震源区与火山口活动区的精细速度结构(如,张明辉等,2020).
除了通过背景噪声互相关计算可提取高阶面波频散,地震也会产生高阶面波信号,且该信号的周期较长(Xu and Beghein, 2019).加强远震高阶面波的研究,与基阶面波结合,可望能够更为准确的约束岩石圈地幔速度结构与上地幔深部的速度结构,为认识上地幔的转换带(410 km和660 km界面)以及相关的动力学过程提供另外重要的手段.由于勒夫波波形在短周期易受高阶面波的干扰(Li and Li, 2015),对于海洋环境下海底地震仪(OBS)记录的勒夫波,其高阶的振幅甚至比基阶要高(Jin, 2015),因此加强高阶面波的研究还能为开展更为准确的高阶与基阶勒夫波融合反演地球内部结构打下重要的基础.此外,近年来发展的伴随成像法(一种全波形成像方法)利用波形的走时与振幅信息,可通过拟合面波与体波的波形,获取更为准确的三维速度模型(Tromp et al., 2008),目前已被运用到青藏高原地区(Chen et al., 2017; Xiao et al., 2020).
通过面波层析成像方法获取的相速度频散曲线,可反演获取岩石圈的S波速度结构.面波的相速度频散不仅与不同深度S波速度结构相关,还受不同深度的P波速度与密度结构的影响.因此,结合其他不同类型的地球物理数据(如体波、瑞利波椭圆率,即ZH比值、重力数据等)开展联合反演,不同数据类型优势互补,不仅可以有效降低单一数据反演S波速度结果的非唯一性,还可有效地约束P波速度、密度或界面信息.如,通过开展面波频散与体波接收函数联合反演可同时约束岩石圈的S波速度与界面结构(Julia et al., 2000).瑞利波频散与ZH比值联合反演可获取准确较高的上地壳(尤其是沉积盆地区域)的S波、P波与密度结构(Lin et al., 2012).在地球物理观测资料不断丰富的今天,开展多种面波层析成像方法研究与多种地球物理数据的联合反演,能有效地获取更为可靠的高分辨率壳幔速度、密度与界面结构.
致谢
感谢编委、责任编委和四名匿名审稿人的建议.感谢李永华研究员提供青藏高原东北缘双台法获取的相速度数据.本文图3—8是使用GMT软件(Wessel et al., 2013)绘制的.
