热流固耦合下微观织构配流副摩擦特性的研究
2022-09-21王宇帆王兆强张娇
王宇帆,王兆强,张娇
(上海工程技术大学机械与汽车工程学院,上海 201620)
0 前言
配流副是轴向柱塞泵的关键摩擦副之一,但是在轴向柱塞泵的运行过程中,配流盘的功率损失高达8%。功率损失的主要来源是润滑界面的摩擦损失和泄漏损失,尤其在低速情况下,由于压力较低,泄漏量较小,摩擦损失占功率损失的绝大部分。摩擦损失一方面取决于润滑油的黏度,另一方面也与配流副摩擦表面形貌和材料有关。随着对柱塞泵性能要求的提高,业内普遍认为表面织构技术在提高柱塞泵效率和承载能力方面起到积极作用。
HAMILTON等利用实验的方法验证了材料表面的微凸起织构能改善润滑性能,他推测微凹坑织构也能产生同样的效果。清华大学汪家道等研究了面接触下不同尺寸的规则凹坑织构对表面摩擦性能的影响,对比了4种不同形貌织构的面接触摩擦润滑实验结果,认为微凹坑的面积率是影响摩擦性能的主要因素。王霄等人利用多重网格法求解了带有微观织构表面的润滑模型,研究发现球冠型织构产生的润滑油膜压力大于圆柱形和圆锥形织构。马晨波研究发现微观织构的深径比在0.005~0.01时具有更好的润滑性能。同年,中科院兰州化学物理研究所胡天昌等对表面织构化的45号钢进行摩擦实验,结果发现:与未进行织构化的材料相比,带有微观织构表面的材料能有效减小摩擦因数,且磨损率也有一定的降低。2013年,中国矿业大学朱华等人在研究微凹坑对摩擦副摩擦性能的影响时发现:当微凹坑织构的面积率在5%时能产生最大的流体动压承载力。韩国学者SEGU D Z及其团队将不同形状的微观织构(圆形、正方形、三角形、椭圆形)混合排列加工到试件表面,并进行不同的排列组合,进行摩擦学实验,结果发现:带有微观织构的试件均能不同程度地降低摩擦因数、减少磨损。近年来,随着对微观织构配流副的理论研究越来越深入,人们发现热流固耦合条件下,微观织构能显著改变配流副油膜压力和温度的分布。
本文作者基于Reynolds方程建立带有方形微观织构配流副的润滑模型,运用有限差分法进行求解,得到离散的压力值、弹性变形和温度值,通过迭代耦合得到误差允许范围内的近似解,并将求得的解导入到MATLAB绘制分布云图,最后改变织构参数分别进行求解,分析了织构参数对润滑性能的影响。
1 建立微观织构配流副润滑模型
在构建带有微观织构配流盘的配流副时,忽略配流盘表面的粗糙度而假定除织构区域外的配流盘表面为绝对光滑。柱塞泵在工作状态下,由于缸体相对于配流盘转动,缸体受到偏载力矩的作用,会向一侧倾斜一定角度。如图1所示,缸体倾斜角度为,配流盘与缸体之间的初始距离为;缸体绕轴逆时针绕转,转速为;矩形织构均匀分布在配流盘表面,深度为,边长为。

图1 微观织构配流副结构模型 图2 微观织构引起的流体动压效应
矩形织构参数是通过润滑油膜厚度引入的。在织构的计算区域内,不同的织构参数对应油膜厚度不同,由于流体的动压效应,导致压力分布不均匀,进而影响油膜的摩擦特性,如图2所示。
2 理论模型的计算
2.1 油厚方程
由图1所示的配流副模型可知缸体相对于配流盘旋转,并发生一定角度的倾斜,此时油膜呈楔形圆环状。为方便计算,将后续求解运算过程均转化为圆柱极坐标系,油厚方程可表达为
=+·sin·tan
(1)
2.2 Reynolds方程
由于此研究中的Reynolds方程是由不可压缩流的Navier-Stokes方程推导而来,所以在求解之前,需要对配流副中的油膜进行必要的假设:(1)忽略油膜惯性力和体积力;(2)流体与固体间无相对滑移;(3)由于油膜厚度极小,忽略油膜厚度方向上的压力变化,由此引申为忽略油膜厚度方向上的温度、黏度变化;(4)润滑油为牛顿流体;(5)忽略由于压力、温度引起的润滑油密度的变化。
此时极坐标下的Reynolds方程为

(2)
式中:为油膜压力;为润滑油黏度;为网格节点处的半径值;为油膜厚度;为网格节点处的角度值。
离散化后运用有限差分法得到解为

(3)
其中:

(4)
边界条件为油膜边界压力值为大气压。
2.3 能量方程
二维能量方程可写成下面形式:


(5)
式中:为热功当量;为润滑油密度;为比热容;为油膜温度;为两摩擦表面平均速度;、分别为、方向上的体积流量。
离散化后运用有限差分法得到解为
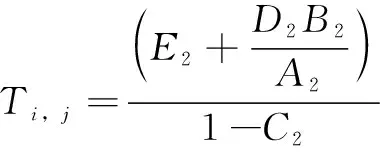
(6)
其中:

(7)
边界条件为油膜边界隔热且初始温度为环境温度。
2.4 弹性变形方程
配流盘是一个圆环形的厚板结构,由于受到表面油膜的压力,配流盘的表面将产生垂直变形,其变形量可以从弹性变形理论得到解释,得到弹性变形方程写作如下形式:

(8)
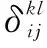
压力分布对弹性变形的影响如图3所示。

图3 压力分布对弹性变形的影响
但是式(8)在点=且=时存在奇异点。为避免奇异点,用奇异点附近的一点(=,=-1)代替奇异点,即:

(9)
离散化后得到总位移变形,为

(10)
其中:

(11)
2.5 黏温-黏压方程
在计算热流固耦合的润滑模型时,需要考虑到温度和压力对润滑油黏度的影响。描述黏度和压力、温度变化规律的方程主要有3种:Barus公式、Roelands公式和Cameron公式。其中Roelands公式公认精确度最高,且数值计算稳定性强,其表达式为


(12)
3 油膜润滑特性
为了计算配流副油膜的润滑特性,给定初始工作条件如下:缸体转速=3 500 r/min;初始油膜厚度=0.032 5×10m;缸体倾斜角度=0.004°;润滑油黏度=0.036 5 Pa·s;环境温度=303 K;微观矩形织构边长=200 μm;深度=5 μm;织构沿圆周方向均匀排布120个,沿半径方向均匀排布10个,共计120×10个。
将计算结果导入到MATLAB,绘制出油膜压力分布云图如图4所示,弹性变形分布云图如图5所示,油膜温度分布云图如图6所示。

图4 油膜压力分布 图5 弹性变形分布 图6 油膜温度分布
4 织构参数对润滑特性的影响
在理想的平行光滑平面的摩擦副中,两平面间的润滑油膜由于没有收敛间隙,无法产生流体动压承载力,但是微观织构的存在使得微观织构边界处客观上存在一个类似的收敛间隙,为流体动压承载力的存在提供了基础。但是不同的织构参数会怎么影响润滑特性?作者将织构边长划分为50、100、150、200、250、300、350 μm,织构深度划分为5、10、20、50、80、100、120、150、200 μm,并逐一进行仿真,来探究不同的织构参数对油膜的润滑特性产生什么样的影响。
图7显示的是矩形织构参数对油膜承载力的影响。在不同织构边长的情况下,随着织构深度的增加,油膜的承载力先增加后减小,最大承载力在织构深度20~50 μm之间,且织构边长越大,承载力越大。但是可以注意到,织构边长越大,其最大承载力对应的织构深度越小,呈现向左移动的现象。

图7 织构对油膜承载力的影响 图8 织构对摩擦力的影响 图9 织构对摩擦因数的影响
图8显示的是矩形织构参数对摩擦力的影响。在不同织构边长的情况下,随着织构深度的增加,摩擦力整体呈现减小的趋势,且织构边长越大,摩擦力会越小。
图9显示的是矩形织构参数对摩擦因数的影响。在不同织构边长的情况下,随着织构深度的增加,摩擦因数整体呈现先减小后增大的趋势,最小摩擦因数在织构深度20~50 μm之间,且织构边长越大,摩擦因数越小。
5 结论
(1)从压力分布图(图4)中可以看出:由于缸体倾斜,润滑油在一侧形成楔形间隙,出现了流体动压效应,使得压力呈单峰形态集中在一侧。同时注意到:在矩形微观织构的边缘,由于油膜厚度的急剧减小,使得油膜出现类似楔形的状态,为动压效应的出现提供了条件。而结果也确实如理论预测的一样,在润滑油表面出现规则排布的压力峰值。
(2)从图7—图9发现:织构边长越大,油膜的润滑特性越好。但是应当注意的是,不同边长的织构对应的最佳织构深度并不相同,随着边长的增大,其最佳深度在减小,最佳深度范围在20~50 μm之间。整体而言,织构越大,摩擦力越小,摩擦因数越小。
(3)本文作者仅从织构的大小、深度方面来考虑其对配流副油膜润滑特性的影响,可以预料的是织构的形状、个数、排列方式等也会对润滑特性产生影响,需要更多的计算结果去支持这一猜想。
