季节性对一类食饵-捕食者模型动力学稳定性的影响

徐王军

（安庆师范大学 数理学院，安徽 安庆 246133）

捕食与被捕食是生态系统中非常重要和常见的种群关系。为了模拟其复杂多样的相互作用，人们提出了多种功能性反应函数，如Holling 型[1-3]、Beddington-DeAngelis 型[4-5]，以及Crowley-Martin 型[6-9]等。因Crowley-Martin型功能性反应函数既依赖于被捕食者种群的密度，又依赖于捕食者种群的密度，所以它更能表现出捕食与被捕食之间复杂多变的种群关系，其表达式为F(x,y)=αx[ (1+hx)(1+fy) ]，其中α、h和f分别表示捕食者的捕获率、处理时间和捕食者之间干扰程度的大小。若h=0 且f=0，则F(x,y)变为Holling-I型；若h＞0且f=0，则F(x,y)变为Holling-II型。

在通常的模型中，种群的增长率和捕食率往往被看作常数。种群的动态行为往往受到季节性变化的影响，尤其是增长率和捕食率。Baek将食饵的增长率乘以季节性正弦周期函数，发现系统存在全局渐近稳定的两食饵灭绝周期解，并研究了季节性对食饵-捕食者系统动力学行为的影响[10]。Yu等在两食饵的增长率中引入季节性正弦周期函数，发现季节性影响使得系统产生了奇异吸引子，展示了季节性对生态系统动力学行为的影响[11]。Alebraheem等对捕食率引入正弦函数，即αs=α(1+εsin(ωt))，其中ε表示季节性程度，是季节性波动的角频率，模拟发现季节性诱导两种群食饵-捕食者模型复杂动力学行为[12]。然而，实际生物链是复杂多种群相互作用。因此，我们在两种群食饵-捕食者系统中引入新的捕食者种群，新捕食种群与原系统捕食者相互竞争，并建立了自治的三种群食饵-捕食者系统，同时，对捕食者的捕获率应用正弦函数，给出了非自治的三种群动力学模型，分析了自治模型正解的有界性、平衡点的存在性以及局部稳定性。此外，数值模拟验证了以上动力学的正确性，并发现季节性对食饵种群和捕食者种群的生存和灭绝具有非常重要的意义。

1 模型建立

通过在两种群食饵-捕食者模型中引入一个新的捕食者种群Z，该捕食者种群捕获原模型中的食饵种群X，并与原模型中捕食者种群Y互相竞争。利用食饵种群遵循Logistic 增长规律和Crowley-Martin型功能性反应函数，建立如下动力学方程组模型：

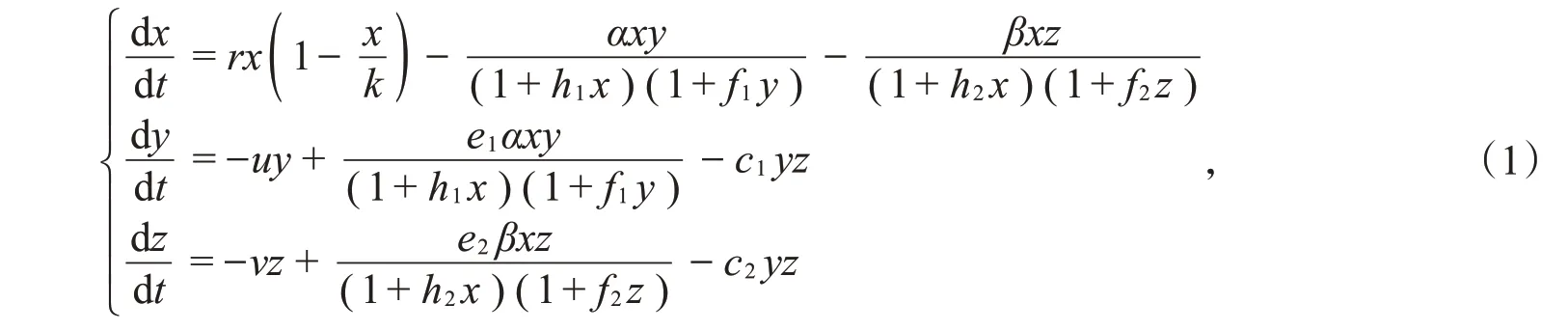
其中x、y和z分别表示食饵种群X、捕食者种群Y和Z的密度，r表示食饵种群X的内禀自然增长率，u和v分别表示捕食者种群Y和Z的死亡率，k表示食饵种群X的环境容纳量，c1和c2表示捕食者种群Y和Z之间相互竞争的大小，α和β分别表示捕食者种群Y和Z的捕获率，h1和h2分别表示捕食者种群Y和Z捕获食饵的处理时间，f1和f2分别表示捕食者种群Y和Z之间干扰程度的大小，e1和e2分别表示捕食者种群Y和Z单位时间内消化食饵的转化率。

为了简便起见，对模型（1）引入无量纲变换：

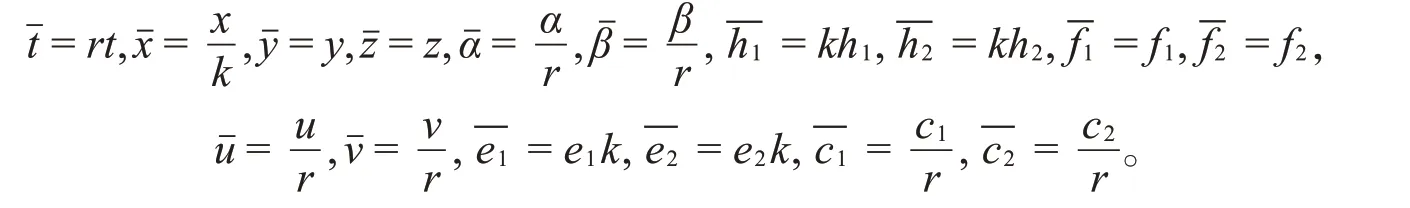
于是，去掉“短横”，得到如下模型：

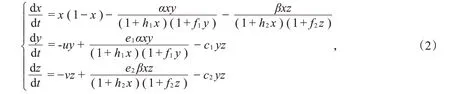
接着，用αs和βs分别代替模型（2）中的α和β，其中αs=α(1+εsin(ωt))，βs=β(1+εsin(ωt))。于是，得到如下非自治微分方程模型：

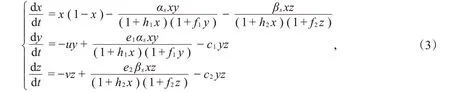
系统（3）的可行域D={ (x,y,z)|x≥0,y≥0,z≥0}，考虑生物学实际意义，只研究解(x(t),y(t),z(t))具有正初始值的情况，即x(0)=x0＞0，y(0)=y0＞0，z(0)=z0＞0，系统中所有的参数都是正常数。

2 自治系统解的有界性

定理1D是系统（3）的正不变集。

证明由系统（3）有

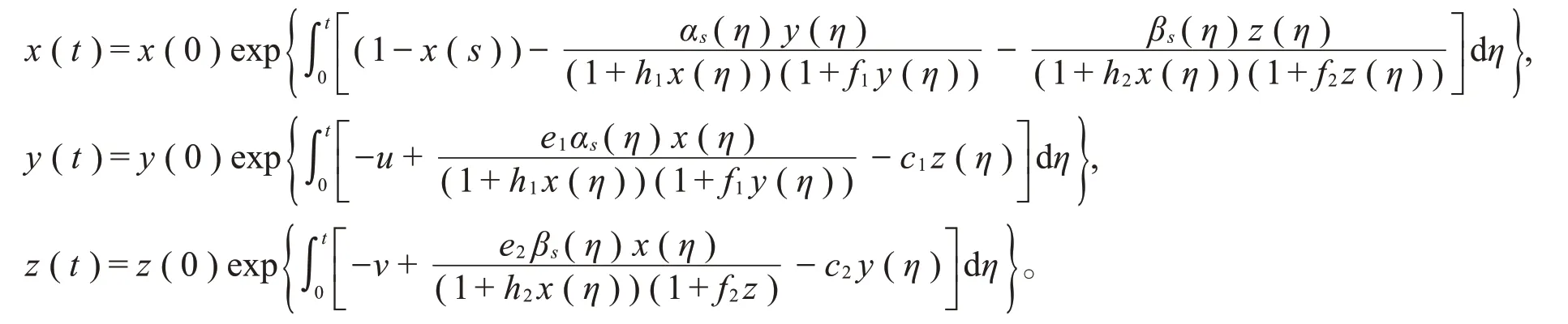
当x(0)＞0，y(0)＞0且z(0)＞0时，必有x(t)＞0，y(t)＞0，z(t)＞0。因此，系统（3）满足正初始值的解可以保持恒正，从而集合D是系统（3）的正不变集。对于系统（2）而言，自治系统（2）的解也都保持恒正，故得到如下自治系统解的有界性定理2。

定理2系统（2）的全部正解在D={ |

(x,y,z)x≥0,y≥0,z≥0}上都是有界的。

证明由系统（2）的第一个方程可知，dxdt≤x(1-x)，解得0 ＜x(t)≤1。

定义一个关于解的和函数L(t)=x(t)+y(t)1+z(t)2，且ρ=min{u,v}，有

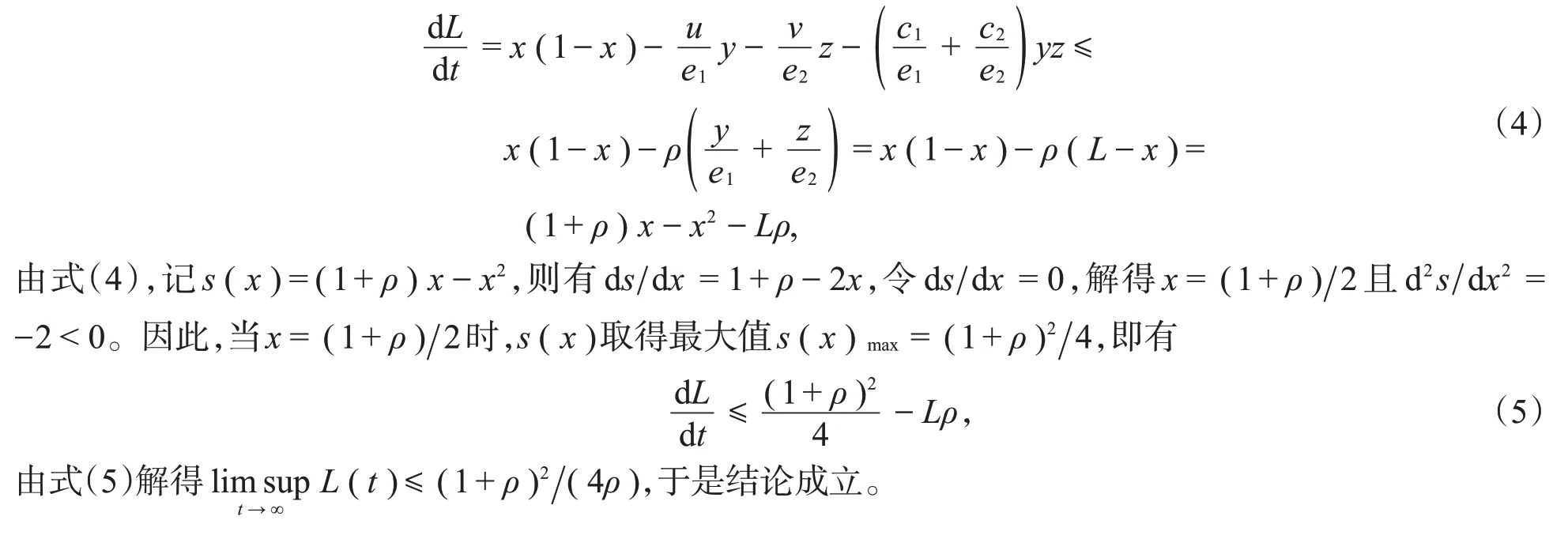
3 平衡点分析

3.1 平衡点的存在性

由方程组（8）可得到P4，因方程组（8）较为复杂，所以通过数值方法验证正平衡点的存在性。

3.2 稳定性分析

分析系统（2）所有非负平衡点的局部稳定性。通过计算每个非负平衡点的雅可比矩阵，利用Lyapunov方法和Routh-Hurwitz判据确定平衡点局部渐近稳定的存在条件。

（I）系统（2）在灭绝平衡点P0处的雅可比矩阵为

于是，P0所对应的特征方程为

解方程（9）得特征值λ1=1，λ2=-u，λ3=-v。显然，λ1＞0，λ2＜0且λ3＜0。因此，灭绝平衡点P0是不稳定的，此时称P0为鞍点。

（II）系统（2）在轴向平衡点P1处的雅可比矩阵为

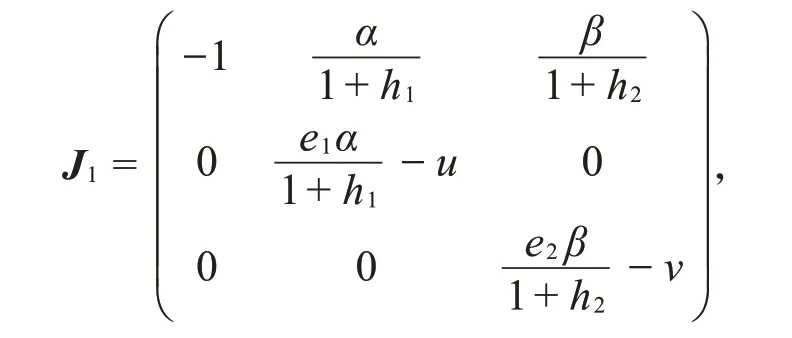
于是，P1所对应的特征方程为

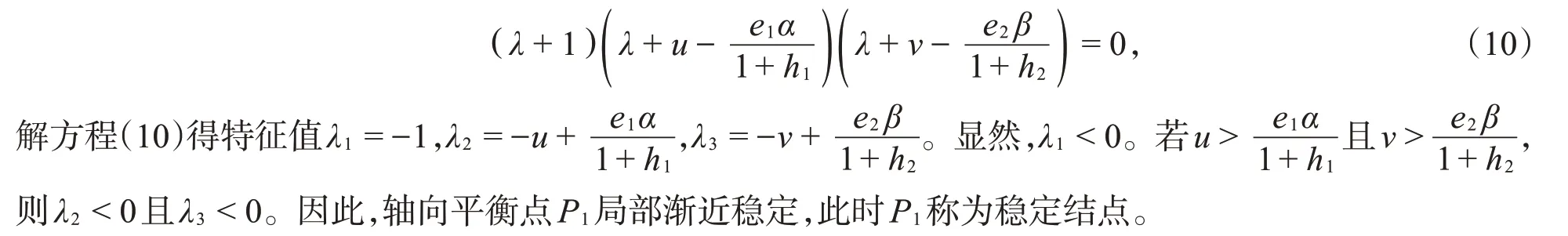
（III）系统（2）在边界平衡点P2处的雅可比矩阵为

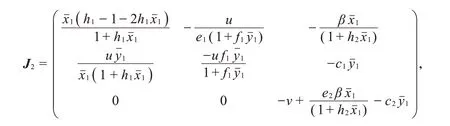
于是，P2所对应的特征方程为

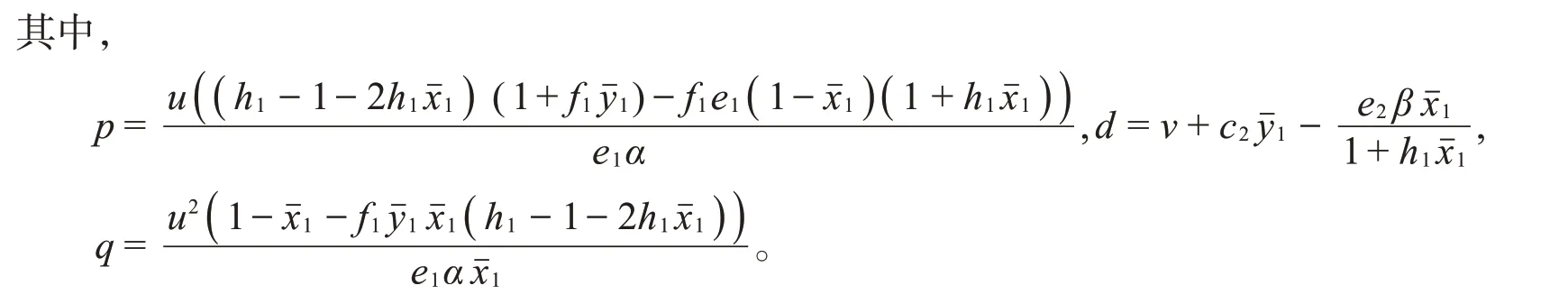
设P2对应的特征值为λi(i=1,2,3)，若

则有λ1+λ2＜0，λ1λ2＞0且λ3＜0，从而它的特征值Re(λi)＜0(i=1,2,3)，于是可得P2局部渐近稳定，此时P2称为稳定结点。

（IV）系统（2）在边界平衡点P3处的雅可比矩阵为

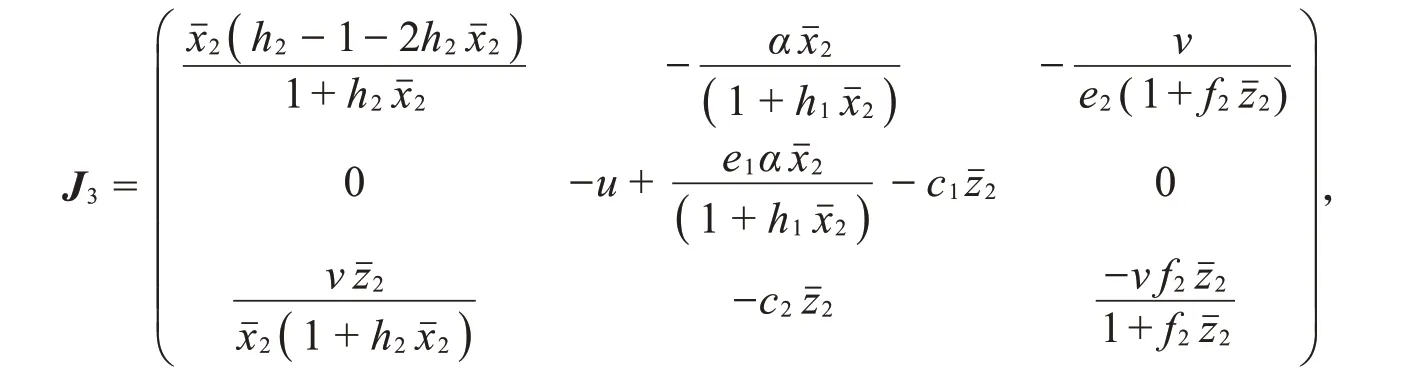
根据在（III）中讨论的边界平衡点P2局部稳定性可知，若P3对应的特征方程是

其中，Aj(j=1,2,3)为实数。同理，设P3对应的特征值为λi(i=1,2,3)，若

则有λ1+λ3＜0，λ1λ3＞0且λ2＜0，从而它的特征值Re(λi)＜0(i=1,2,3)，于是可得P3局部渐近稳定，此时P3称为稳定结点。

（V）系统（2）在正平衡点P4处的雅可比矩阵是

根据罗斯-霍维兹判据准则，如果满足下列条件：

由条件（15），解得

若条件（16）成立，即P4对应的所有特征值都有负的实部，则正平衡点P4是局部渐近稳定的。

4 数值模拟

下面，通过数值模拟来验证平衡点的稳定性，并用时间序列图、相图以及分岔图展示季节性对食饵-捕食者系统动力学行为的影响。图1中，固定参数α=0.9，u=0.2，e1=1.6，h1=2，f1=0.3，ω=0.1。当系统无季节性强度(ε=0)时，食饵种群X与捕食者种群Y的相图曲线趋于一个稳定点（SP）P2(0.386,1.897,0)（图1（a））；当系统存在季节性强度(ε=0.05)时，食饵种群X与捕食者种群Y的相图曲线趋于一个稳定的极限环（LC）（图1（b））。因此，季节性强度对生态系统的稳定性具有重要的作用。

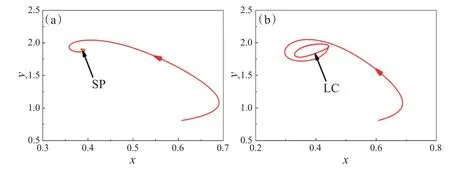
图1 系统（3）关于两种群食饵X和捕食者Y的相图。（a）ε=0；（b）ε=0.05

图2 中，固定参数ω=0.1，e1=0.8，e2=0.85，c1=0.06，c2=0.05，u=0.42，v=0.5，f1=0.5，f2=0.45，h1=2，h2=2.5，α=4.3，β=5。当系统无季节性强度(ε=0)时，随着时间的不断演化，捕食者种群Y、Z和食饵种群X的密度渐渐表现出周期性振荡的现象（图2（a））；当系统存在季节性强度(ε=0.25)时，随着时间的不断演化，捕食者种群Y、Z和食饵种群X的密度表现出概周期振荡的现象（图2（b））。因此，季节性强度对维护生态系统的稳定性具有重要的影响。

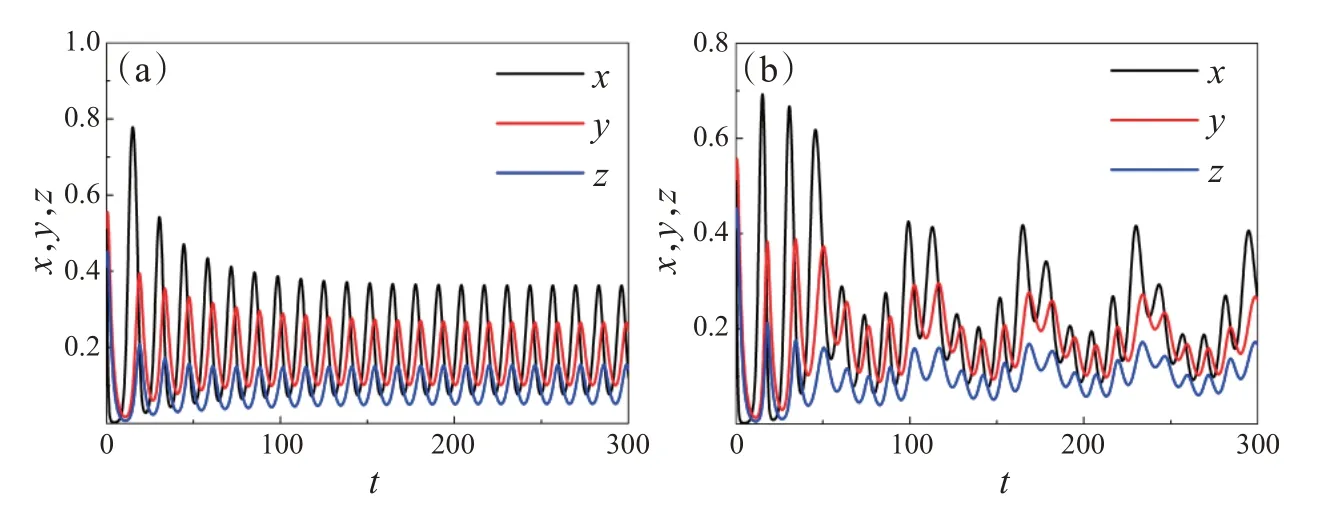
图2 系统（3）关于三种群的动力学行为时间序列图。（a）ε=0；（b）ε=0.25

图3 中，固定参数ω=0.1，e1=0.8，e2=0.85，c1=0.06，c2=0.05，u=0.42，v=0.5，f1=0.5，f2=0.45，h1=2，h2=2.5，α=4.3，β=5。当系统无季节性强度(ε=0)时，食饵种群X与捕食者种群Y、Z的相图曲线趋于一个稳定的极限环（图3（a））；当系统存在季节性强度(ε=0.25)时，食饵种群X与捕食者种群Y、Z的相图曲线呈现出混沌现象（图3（b））。

图3 系统（3）中三种群共存时的三维相图。（a）ε=0；（b）ε=0.25

图4 中，固定参数ω=0.18，e1=0.8，e2=0.83，c1=0.06，c2=0.05，u=0.57，v=0.6，f1=0.38，f2=0.35，h1=2.2，h2=2，α=4.3，β=4.2。当系统无季节性强度(ε=0)时，随着时间的不断演化，捕食者种群Y、Z和食饵种群X的密度曲线渐渐趋于一个定值，即P4(0.289,0.131,0.151)（图4（a））；当系统存在季节性强度(ε=0.15)时，随着时间的不断演化，捕食者种群Y、Z和食饵种群X的密度曲线表现出周期振荡的现象（图4（b））。因此，季节性强度对维护生态系统的稳定性具有关键性作用。

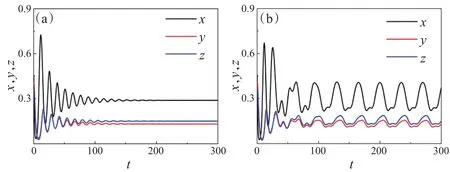
图4 系统（3）关于三种群的动力学行为时间序列图。（a）ε=0；（b）ε=0.15

图5 中，固定参数ω=0.18，e1=0.8，e2=0.83，c1=0.06，c2=0.05，u=0.57，v=0.6，f1=0.38，f2=0.35，h1=2.2，h2=2，α=4.3，β=4.2。当系统无季节性强度(ε=0)时，食饵种群X与捕食者种群Y、Z的相图曲线趋于一个稳定点P4(0.289,0.131,0.151)（图5（a））；当系统存在季节性强度(ε=0.15)时，食饵种群X与捕食者种群Y、Z的相图曲线趋于一个稳定的极限环（图5（b））。

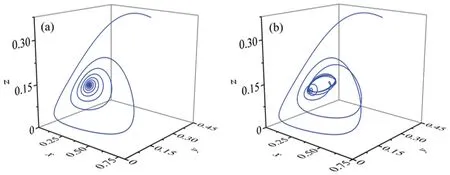
图5 系统（3）中三种群共存时的三维相图。（a）ε=0；（b）ε=0.15

图6 中，固定参数ω=0.18，e1=0.8，e2=0.83，c1=0.06，c2=0.05，u=0.57，v=0.6，f2=0.35，h1=2.2，h2=2，α=4.3，β=4.2。当系统无季节性强度(ε=0)时，随着f1的增大，系统经历从振荡状态跨过临界值达到稳定状态，其中临界值f1c=0.15，当f1∈(0.15,0.4)时，系统（3）中P4是局部渐近稳定的（图6（a））；当系统存在季节性强度(ε=0.15)时，随着f1的增大，系统经历从振荡状态跨过临界值达到稳定状态（图6（b）），其中临界值f1c=0.45，与图6（a）相比，当系统受到季节性影响时，临界值越大，则不利于生态系统稳定。

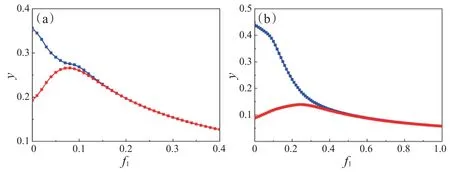
图6 系统（3）中参数为f1的捕食者Y分岔图。（a）ε=0；（b）ε=0.15

图7 中，固定参数ω=0.18，e1=0.8，e2=0.83，c1=0.06，c2=0.05，u=0.57，v=0.6，f1=0.38，f2=0.35，h1=2.2，h2=2，α=4.3，β=4.2。当系统（3）中只有食饵种群X和捕食者种群Y共存，而捕食者种群Z灭绝时，随着ε的减小，系统经历从振荡状态跨过临界值达到稳定状态，其中临界值εc=0.1。当ε∈(0,0.1)时，食饵种群X和捕食者种群Y两种群系统是稳定的（图7（a））；当系统（3）中食饵X、捕食者Y和Z三种群都共存时，随着ε的减小，系统经历从振荡状态跨过临界值达到稳定状态（图7（b）），其中临界值εc=0.2。与图7（a）相比，当系统为三种群相互作用时，临界值越大，并且多种群相互作用有利于系统的稳定。

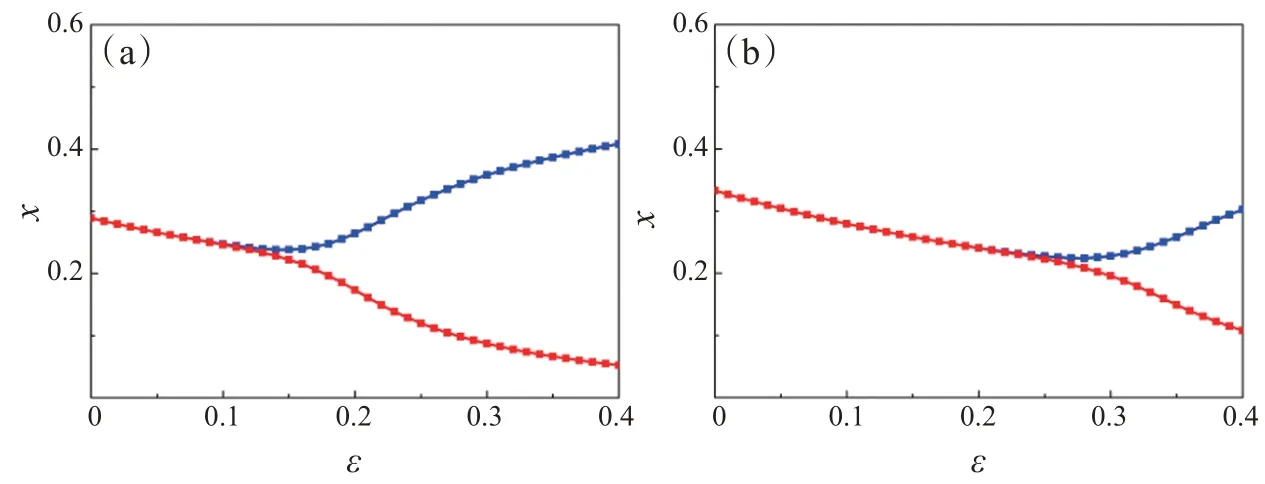
图7 系统（3）中参数为ε的捕食者Y分岔图。（a）ε=0.1；（b）ε=0.2

5 结论

本文根据食饵种群遵循Logistic 增长和选取Crowley-Martin 型功能性反应函数建立了自治的三种群动力学模型，并对捕获率引入季节性变化的正弦周期函数，从而给出非自治的三种群动力学模型。数值模拟结果和分析表明，在季节性强度作用下，通过在两种群食饵-捕食者系统中引入新的捕食者种群，多种群相互作用能够增大季节性强度临界值，使得三种群的食饵-捕食者系统稳定变强；季节性强度也能诱导系统产生稳定的极限环和混沌等现象。季节性强度过大会增加捕食者灭绝的可能性，所以我们要控制季节性强度对捕食者捕获食饵的影响。研究结果显示：春夏季节，捕食者捕获食饵的效率会更高，那么三种群之间互相共存的可能性就比较大；而在秋冬季节，捕食者捕获食饵的效率会低一些，从而物种之间互相共存的可能性就比较低。因此，季节性因素对种群持久性和灭绝性具有非常重要的意义。