二维活塞泵空间凸轮的建模与实验

2022-09-20丰章俊

液压与气动 2022年9期

丰章俊，陈勇，阮健

(1.浙江同济科技职业学院机电工程学院，浙江杭州 311231；2.浙江工业大学机械工程学院，浙江杭州 310023)

引言

相较于其他传动方式，液压传动在功率密度方面有无以伦比的优势[1]。随着电气化时代的到来，液压传动技术中的电静液作动器(Electro-hydrostatic Actuator，EHA)[2-3]成为研究热点。一般来说，EHA是集成了无刷直流电机(BLDCM)、双向电动泵、蓄能器、单项阀、安全阀、液压缸的独立液压系统，如图1所示。它可以完全省去复杂的液压油管，比传统的分布式液压系统具有更高的集成程度；可以通过控制电动泵排出的流量来控制液压缸活塞的动作，不仅节省了伺服阀昂贵的成本，也避免了阀配流带来的节流损耗问题，大大提高了液压系统的效率[4]。

图1 EHA原理图Fig.1 Principle diagram of EHA

早在上世纪末，美国军方联合航空指挥部组织多兵种专家启动多电飞机计划。美国洛克希德马丁摒弃了传统液压系统，为F/A-18、F-16战机安装上新型的EHA[5-6]。实验证明用EHA作为舵机可以提高有效性、可靠性、易维护性，且有效降低了起飞重量，节省了燃油消耗，减少了易受轻武器攻击的面积。此外，EHA在车辆[7]、工程机械、潜水设备[8]、机器人[9]等领域也具有广阔的发展前景。

未来液压泵的发展需要更多地考虑EHA的工况特点，如为了达到更高的功率密度，需要高速化、高压化；为了节能和减少发热[10]，泵要有更高的效率；为了适应急停急起的工况，摩擦副需要有更长的可靠性和寿命。由此来看，浙江工业大学阮健教授团队[11]设计的二维活塞泵利用空间凸轮和滚子机构使活塞具有往复运动和旋转运动2个自由度，往复运动用于吸排油，旋转运动用于配流。这种设计结构简单、紧凑，摩擦副可靠性较高，十分适合作为EHA的液压动力源。

空间凸轮是二维活塞泵的关键零件，在很大程度上影响着泵的振动、噪声、寿命、可靠性等性能。金丁灿等[12]分析了圆锥滚子与空间凸轮的空间接触关系，建立了接触曲面的模型；张振炎等[13]分析了空间凸轮的工艺需求，设计了可行的加工工艺，得到了可靠的凸轮零件。为了设计和制造出性能更好的泵，完善凸轮的设计理论相当重要。

1 二维活塞泵原理

二维活塞泵的结构如图2所示，为了显示内部结构，缸体已被剖开。泵工作时，电机通过传动轴带动活塞轴作旋转运动。滚子与活塞轴固连，在空间凸轮的支撑下，在旋转的同时带动活塞轴一起作轴向往复运动。活塞轴与缸体之间配合，形成2个密封容腔，其体积周期性变化，完成吸排油。配流是通过活塞轴上的配流槽与缸体上的配流窗口配合完成的，活塞轴的旋转运动使两者的重合面积不断变化，在容腔被压缩时，配流槽与排油窗口连通；在容腔被扩张时，配流槽与吸口窗口连通。这样的设计使活塞的双自由度运动被充分利用。

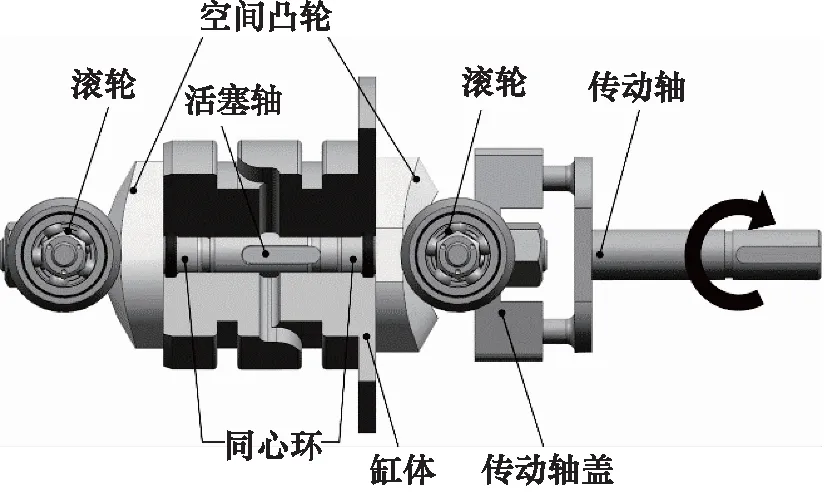
图2 二维活塞泵结构图Fig.2 Structure of two-dimensional piston pump

2 空间凸轮建模

平面凸轮的建模过程是先求得滚子中心相对于凸轮的运动轨迹，称为理论轮廓曲线，然后以此曲线上的点为圆心，作一系列滚子圆，滚子圆的内包络线即为实际轮廓曲线。这种方法对平面凸轮来说是准确的，但是在设计空间凸轮时会产生一些误差。金丁灿等[12]在提出凸轮的数学模型时，假设了圆锥滚子和空间凸轮的接触线为直线，然而事实是除了最低点和最高点外，在滚子上下坡时接触线都不是直线，于是有很小的误差。为了更精确地计算空间凸轮廓面，需要使用TSAY等[14]提出的数值方法。

2.1 三维空间包络理论

首先在任意一个三维笛卡尔坐标系中，用u1，u2表示曲面族上特定曲面的参数，以ζ表示曲面运动轨迹的参数，则运动轨迹上的无数个曲面所形成的曲面族可表示为：

r=r(u1,u2,ζ)

(1)

空间凸轮的廓面是曲面族中无数条特殊曲线组成的，根据包络理论[12]，这些曲线应满足以下方程：

(2)

理论上可以通过式(2)消除3个参数u1，u2，ζ中的一个，再代入式(1)，并检查是否存在奇异点，即可获得包络面的方程。

实际计算空间凸轮廓面时，因为参数ζ描述了滚子的位置，所以把每一个ζ的值代入到式(2)，求解后就能获得该位置的滚子与空间凸轮接触线，排除奇异点后，所有的接触线就组成了一个完整的包络面。因此，推导的步骤为：

(1) 建立滚子坐标系和固定坐标系，推导运动一个周期后，圆锥滚子回转面形成的曲面族；

(2) 根据包络理论计算滚子上的接触线；

(3) 将接触线在滚子坐标系中的位置代入固定坐标系中的曲面族方程，得到最终的廓面。

2.2 曲面族方程

曲面族是由圆锥滚子在旋转和往复的复合运动产生的，圆锥滚子的尺寸参数含义如图3a所示；图3b表示了滚子与空间凸轮廓面的空间关系。

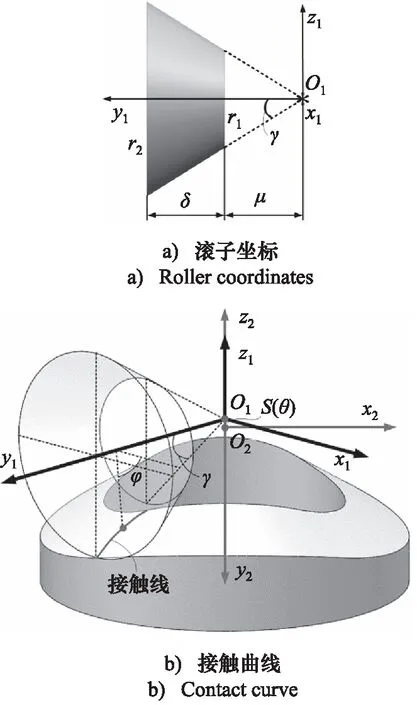
图3 空间凸轮廓面形成原理Fig.3 Principle of spatial cam contour formation

在滚子坐标系中，圆锥回转面的向量形式表达为：

r1=r1(δ,φ)=x1i1+y1j1+z1k1

(3)

其中，x1=r2cosφ；y1=l；z1=-r2sinφ。

式中，i1，j1，k1—— 滚子坐标系中沿O1x1，O1y1，O1z1方向的单位向量

r1—— 滚子小端半径

δ—— 滚子高度

γ—— 滚子半锥角

l—— 大端与顶点距离

μ—— 小端与顶点距离

φ—— 接触点与x1轴的夹角

θ—— 滚子绕z2轴的旋转角度

根据二维泵的设计理论[11]，滚子绕空间凸轮的z2轴旋转并且作轴向往复运动。转角为θ时，圆锥回转面经过坐标变换后产生了曲面族，根据坐标旋转变换和平移变换的原理，曲面族方程可以表示为：

[0 0S(θ)]

(4)

其中， 0≤φ≤π。

式中，r2—— 滚子大端半径

S(θ) —— 滚子轴向位移与绕z2轴旋转角度的函数

经过坐标变换后得到的曲面族方程也可以在固定坐标系中表达为：

r2=(x2,y2,z2)=x2i2+y2j2+z2k2

(5)

其中，x2=r2cosφcosθ+lsinθ；y2=-r2cosφsinθ+lcosθ；z2=-r2sinφ+S(θ)。

式中，i2，j2，k2—— 滚子坐标系中沿O2x2，O2y2，O2z2方向的单位向量

2.3 滚子上的接触位置

根据包络条件可以计算出滚子上接触的位置。包络条件表示为：

(6)

记：

(7)

其中，xφ=-r2cosθsinφ；yφ=r2sinθsinφ；

zφ=-r2cosφ。

又记：

(8)

其中，xδ=tanγcosθcosφ+sinθ；

yδ=-tanγsinθcosφ+cosθ；zδ=-tanγsinφ。

通过计算和化简，得到：

(9)

其中，xn=-r2tanγsinθ+r2cosθcosφ；

yn=-r2tanγcosθ-r2sinθcosφ；zn=-r2sinφ。

由于在式(9)中r2>0，故曲线族中不存在奇异点。根据式(9)继续计算可以得出滚子上的接触角φ。

(10)

其中，xθ=-r2sinθcosφ+lcosθ；yθ=-r2cosθcosφ-lsinθ；zθ=S′(θ)；S′(θ)=dS(θ)/dθ。

通过计算和化简，得到方程：

(11)

其中，H=-S′(θ)cosγ；I=r2tanγ+l。

方程式的解为：

(12)

滚子的运动轨迹为等加速等减速运动，在一个周期内旋转的轴向位移和导函数与转角的关系分别表达为：

(13)

(14)

式中，h为空间凸轮的行程。

设置参数如表1所示，在MATLAB中编写程序，计算出的滚子上的接触角度如图4所示，凸轮廓面如图5所示。

图4 滚子上的接触角度φFig.4 Contact angle φ on roller

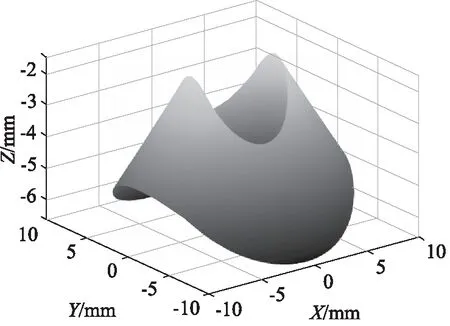
图5 空间凸轮廓面Fig.5 Profile of spatial contour

表1 空间凸轮建模参数Tab.1 Modeling parameters of spatial cam

2.4 空间凸轮的压力角

压力角的定义为圆锥滚子受力方向与轴向运动方向的夹角，根据定义有：

α=arccos(n1·m1)

(15)

式中，m1—— 轴向方向单位向量，m1=(0,0,1)

n1—— 空间凸轮廓面法向方向单位向量，

通过计算得到的压力角α如图6所示，在最高点和最低点处的压力角最小，为30°；在中间位置时压力角最大，此压力角最大为38.57°。

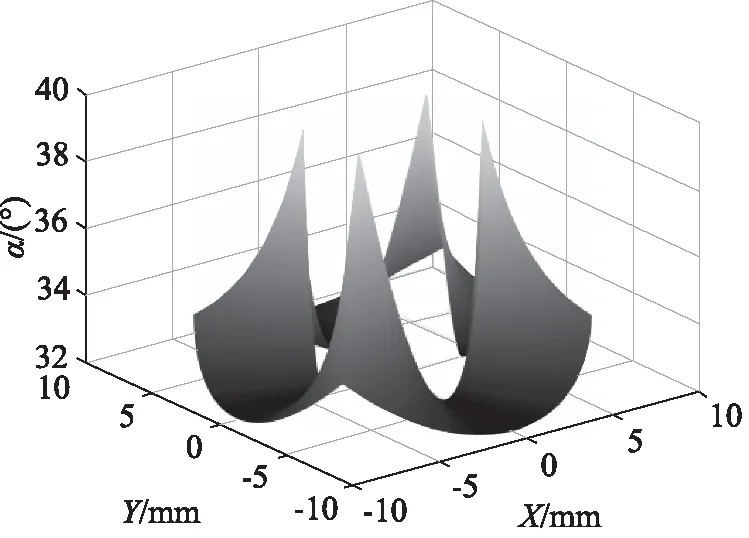
图6 压力角αFig.6 Pressure angle α

2.5 空间凸轮的曲率半径

曲率是描述空间凸轮弯曲程度的重要概念，与其相关的曲率半径影响着凸轮的加工难度、精度和成本[15]。上文中通过MATLAB计算得到的数据都是离散值，因此无法得到曲率半径的解析解。根据KROON D J[16]提出的三角网格曲面上离散曲率算法，先用最小二乘法拟合得到顶点领域内的曲面方程：

f(x,y)=ax2+by2+cxy+dx+ey+f

(16)

式中，a，b，c，d，e，f为拟合曲面的常数项。

然后利用特征向量和特征值计算主曲率、平均曲率和高斯曲率，得到平均曲率Km如图7所示。在中间位置得到最小的平均曲率为-8.75×10-3m-1。

图7 平均曲率KmFig.7 Mean curvature Km

3 仿真与实验

3.1 仿真

从图4中看出在空间凸轮的最高点和最低点的中间位置时接触角度φ最大。在UG中建立空间凸轮模型和滚子模型，并把滚子装配到空间导轨的中间位置，如图8a所示，再将滚子向轴向方向下移0.0001 mm，使滚子与凸轮干涉。通过提升提和布尔运算求出干涉部分体积，如图8b所示。

图8 建模结果对比Fig.8 Comparison of modeling results

得到文献[12]建模方法的干涉部分体积为0.000275 mm3，用空间包络法得到的干涉部分体积为0.000013 mm3。用文献[12]方法建模得到的干涉部分的形状如图8c所示，为一个内圈较宽，外圈较窄的楔形；用三维空间包络法建模得到的干涉部分的形状如图8d所示，为一个宽度均匀的条形，且宽度很小。仿真说明三维空间包络法具有更好的精度。

3.2 实验

空间凸轮的加工使用了VMC850三轴立式加工中心。通过UG建立如图9a中的空间凸轮三维模型，导入到Cimatron软件后，选择4 mm球头铣刀，再选择从内到外的螺旋线走刀路径，软件会根据球头直径和刀具路径自动补偿。空间凸轮使用了40Cr材料，调制后硬度可达HB220～HB250。加工时先用6 mm平头铣刀粗加工两次，留余量0.1 mm，再真空淬火，使硬度达到HRC55～HRC58，然后用4 mm球头铣刀精加工两次。加工出的空间凸轮实物如图9b所示，经过三坐标检测仪测量，发现最大偏差为0.019 mm，平均偏差为0.003 mm，最小偏差为-0.016 mm，三坐标检测结果如图9c所示。