气液联合式碎石器建模与仿真分析
2022-09-20赵彦军毛文亮
赵彦军, 毛文亮
(甘肃机电职业技术学院 机械工程学院, 甘肃天水 741001)
引言
气穴是流体机械中常见的一种有害现象。气穴的发生不仅影响了流体传动的连续性,同时受挤压气泡在溃灭过程中产生强烈的振动和噪声,导致系统内局部区域出现高压、高温,更严重的是会在零件表面形成气蚀[1-3]。
作为一种冲击振动机械,气液联合式碎石器具有能量密度高、稳定性好、结构紧凑、适应性强等特点,经常与液压挖掘机等工程机械结合[4-5]。
冲击能体现着气液联合式碎石器的工作能力。黄雪琴等[6]建立了阀芯和冲击活塞的动力学模型,同时基于MATLAB平台开发了冲击性能优化设计代码。丁问司等[7-8]基于弹性体一维振动瞬态应力波传播理论,建立了活塞与钎杆冲击过程的双柔性杆共轴纵向碰撞计算模型,同时分析了冲击过程中钎杆和活塞的应力波传播规律及各截面的冲击动力特性。张立强等[9]分析了氮气腔及蓄能器中压力与容积等工作参数对冲击性能的影响,同时采用正交试验优化相应的参数。刘忠等[10-11]创建了碎石器和岩石力学特性的数学模型,并运用MATLAB和AMESim软件进行了联合仿真,同时获得了氮气室反馈压力、工作流量及岩石特性对其工作性能的影响。
以上为碎石器冲击性能方面的研究。然而,迄今为止,几乎没有公开出版的有关气液联合式碎石器气穴特性的相关研究。仅有的文献是邓龙等在阐述碎石器工作过程的基础上,采用联合仿真模型分析了碎石器工作过程中不同时刻对应的内部流场,确定了其中出现气蚀的原因,同时将计算结果与实际工程中出现的气蚀真相进行了对比[12]。可是,该研究仅仅针对现有参数进行分析,并未讨论结构参数、工作参数及油液基本属性参数变化时对气穴强度的影响。鉴于此,本研究在介绍气液联合式碎石器工作原理的基础上创建了主运动件及内部流道结构的数学模型,同时搭建了包含动力系统及控制系统的整机AMESim仿真模型。之后根据工况条件类型及对应取值范围设计了正交试验方案,在此基础上详细分析了不同试验条件对应活塞后腔最低压力及冲程最大速度曲线的变化规律,获得了主要影响因子及增加后腔最低压力同时提高打击速度的条件,从而为提升整体性能提供了坚实理论基础。
1 主运动件数学模型
1.1 数学模型的假设条件
气液联合式碎石器内部油道结构复杂,表征流动特性的相关物理量变化剧烈。这样,即使艰难地创建出相关数学模型,也会因为刚性问题影响求解精度,甚至出现无法求解的情形。因此,基于研究的主要目标进行必要的假设,从而实现既能够准确反映实际的物理过程,也能够达到快速计算的目的。具体假设条件如下:
(1) 不考虑液压油的黏温及黏压特性;
(2) 采用定量泵对碎石器进行供液;
(3) 根据研究目标,可忽略油液中瞬时压力波的传递时间;
(4) 碎石器内部与油液相互作用的零件视为不变形的绝对刚体,其余系统的部件按实设置;
(5) 忽略温度变化对氮气腔中氮气实际状态方程的影响;
(6) 蓄能器隔膜的质量及变形视为理想状态。
1.2 活塞的数学模型
运动活塞是碎石器中能量转换的执行部件,将液压能及氮气提供的弹性势能转化为机械能冲击钎杆对外做功。根据实际工作中所受作用力,可得活塞所有状态受力平衡总方程:
(1)
式中,Fi(KL,dxp/dt) —— 液动力
Ff(dxp/dt,Δp) —— 黏性摩擦力
Fr(pl,p1,p2) —— 液压卡紧力
mpgcosβ—— 重力分量
mpd2xp/dt2—— 惯性力
PNAN0—— 后端面受所受氮气作用力
Fp(p1,p2) —— 轴向液压力
活塞轴向液压力方程为:
Fp(p1,p2)=p1A1-p2A2
(2)
式中,p1—— 活塞前腔压力
A1—— 活塞前腔作用面积
p2—— 活塞后腔压力
A2—— 活塞后腔作用面积
液压卡紧力及黏性摩擦力方程分别为:
Fr=αldΔp
(3)
(4)
式中,α—— 阻力系数,α=0.02~0.025
l—— 环缝的密封长度
d—— 起密封作用的内圆柱面直径
Δp—— 压差
ε—— 环缝偏心率
h—— 同心环缝的径向厚度
μ—— 动力黏度
u—— 活塞速度
式中的“+”、“-”号确定原则:活塞运动方向与压差方向一致时,式(4)取“-”,否则取“+”。
液动力方程为:
(5)
式中,Cd—— 阀口流量系数
dxp/dt—— 活塞移动速度
ρ—— 油液密度
1.3 阀芯的数学模型
阀芯是碎石器中的关键部件,其运动形式为间歇性,即当信号孔中压力发生变化时,阀芯才会动作,其余时间都处于静止状态。根据所受作用力,可得阀芯所有状态受力平衡总方程:
(6)
式中,Ff(dxv/dt,Δp) —— 黏性摩擦力
Fr(p) —— 液压卡紧力
mvg—— 重力
mvd2xv/dt2—— 惯性力
Fv(p1,p3) —— 轴向液压力
需要说明的是,由于速度较低同时阀芯上设计了保压结构,因此可忽略液动力的影响。结合阀芯结构参数,可得轴向液压力方程:
Fv(p1,p3)=p3A1v-p3A2v+p3A3v
(7)
式中,p3—— 回油压力
A1v—— 阀芯下端作用面积
A2v—— 阀芯上端作用面积
A3v—— 阀芯信号端作用面积
阀芯所受液压卡紧力及黏性摩擦力同活塞,此处不再赘述。
1.4 蓄能结构的数学模型
传统蓄能机构包括高低压蓄能器。对于碎石器来说,也可将氮气腔归入蓄能结构中。
蓄能器的气体状态方程:
(8)
式中,p0—— 初始压力
V0—— 初始容积
pa0—— 工作压力
Va0—— 工作容积
C0—— 初始状态常数
k—— 气体绝热指数,常取k=1.3~1.5
获取氮气变化过程中最大容积变化量方程:
ΔV=Vnmax-Vnmin=An0s
(9)
式中, ΔV—— 最大变化容积
Vnmax—— 最大容积,即初始容积
Vnmin—— 最小容积
An0—— 活塞端部面积
s—— 活塞行程
由此可得氮气腔工作容积比方程:
(10)
在活塞运动过程中,假设某一点的位移为x,对应氮气压力为pn,则氮气腔体积为:
Vn=Vnmin+An0x
(11)
在碎石器工作过程中,由于冲击频率较高,氮气腔内的热量来不及与外界交换,故按绝热变化可得氮气腔中的压力:
(12)
式中,pnmax—— 最大压力
pnmin—— 最小压力,即初始压力
在单个冲程运动中,氮气腔对活塞所做的功为:
(13)
式中,Φ—— 氮气与液压力做功比
K—— 考虑冲程运动阻力引入的修正系数
E—— 单次冲击功
整合上述方程可得氮气腔的初始容积、初始压力及最大压力,见以下方程:
(14)
(15)
(16)
1.5 内部流道的数学模型
碎石器内部流道由很多形状各异的孔槽组成,是一个多容腔互联系统。容腔内部与容腔之间的物理参数变化很大,同时参数之间的耦合性很强。因此,在建模过程中必须重视这种剧烈变化,否则会导致结果严重失真。
基于连续性方程可得碎石器的流量平衡基本微分方程。其中,高压油流量平衡总方程为:
(17)
式中,Qi—— 液压泵输出流量
Qha(dVh/dt) —— 高压蓄能器排液流量
Ql(dxp/dt,Δp) —— 内部总泄漏流量
Qp(dxp/dt) —— 活塞运动所需流量
Qv(dxv/dt) —— 阀芯运动所需流量
Qc(dp/dt) —— 油液压缩流量
低压油液流量平衡总方程为:
(18)
式中,Qpvo(dxp/dt,dxv/dt) —— 经活塞及阀芯流入回油通道的流量
Qo(dxo/dt)—— 回油通道的总流量
2 AMESim仿真模型及正交试验方案
2.1 主运动件仿真模型
1) 活塞运动分析及仿真建模
从运动过程可知活塞一直处于回程与冲程的连续往复动作状态中(忽略活塞打击后停顿的时间)。其动力来源于高压油和氮气压力,即高压油通过油道进入缸体全圆周开口环缝中进一步作用于活塞凸肩,氮气直接作用于活塞后端面。首先获取活塞结构原理图,见图1。
由图1可知,活塞结构为一系列具有台阶面的圆柱体,其上凸肩与缸体内部孔道共同配合组成的阀口形式为滑阀。因此,将缸体通油结构并入活塞仿真模型之中。对应结构包括活塞前部与中部的液压密封,后部气压密封;前端常高压油道、中部信号通道与回油通道以及这些通道对应液压容腔。根据轴肩与对应缸体油道构成的阀口形式建立活塞仿真模型,见图2。

图1 活塞结构示意图Fig.1 Schematic diagram of piston structure
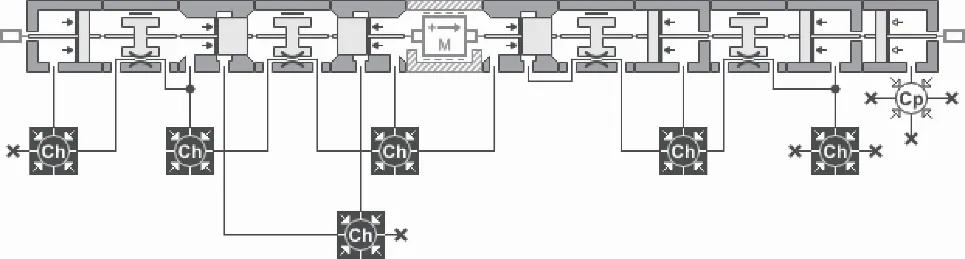
图2 活塞仿真模型Fig.2 Piston simulation model
2) 阀芯运动分析与仿真建模
从运动过程可知阀芯是间歇性动作的,即在活塞回程末段阀芯缓慢开启;在活塞冲程到低压腔与信号腔沟通时缓慢关闭,其余时间均处于静止状态。阀芯开启过程中,信号腔中高压油作用于环缝端面上,从而克服重力及两端压差打开阀芯;在关闭过程中,在端面压差及自重的共同作用下关闭阀芯。首先获取阀芯结构原理图,见图3。

图3 阀芯结构示意图Fig.3 Schematic diagram of spool valve structure
由图3可知,阀芯结构同样是一系列具有台阶面的圆柱体,其上凸肩与阀套内部孔道共同配合组成的阀口形式也为滑阀。因此,将阀套通油结构并入阀芯仿真模型之中。对应结构包括高低压容腔的间隙密封,回油通道孔径,各种油道及对应容积。根据阀芯轴肩与对应阀套油道构成的阀口形式建立阀芯仿真模型,见图4。

图4 阀芯仿真模型Fig.4 Spool simulation model
3) 蓄能机构仿真建模
在仿真建模时高压蓄能器直接调用液压库中标准模型同时考虑进口阻尼。对于氮气腔,则选择气压库中带壁面的可变容腔即可。
2.2 内部油道模型分析
为模拟碎石器内部流道的沿程及局部阻尼损失,就需要利用管道子模型及液压阻尼元件。为了选择符合实际的管道子模型,结合碎石器的结构特点,可参考以下3个重要物理量来进行。
1) 长度/直径(L/D)
当比值小于6时,可忽略流体质点间及流体与管壁间的摩擦力,此时可选择不考虑压降的管道子模型,即没有阻性的管道。
2) 耗散数Dn
当该值小于1时,意味着管道中流体质点的波动效应非常明显;当该值介于0.001~1之间,则需要考虑与频率相关的摩擦模型。其方程为:
(19)
式中,ν—— 运动黏度
c—— 流体中的声速
R—— 管道半径
L—— 管道长度
3) 管道中压力波的传输时间方程为:
(20)
在管道中若波动效应起主导作用,就必须考虑惯性,同时时间步长要小于压力波传输时间。
2.3 整机仿真模型
根据主运动件及内部油道的建模分析可得气液联合式碎石器的AMESim模型。作为执行元件,需要动力系统供能后才能正常工作。因此,获取碎石器所在液压系统,其原理见图5。

1.油箱 2.吸油过滤器 3.溢流阀 4.动力源 5.单向阀6.气液联合式碎石器图5 气液联合式碎石器系统原理图Fig.5 Schematic diagram of gas-liquid combined lithotripter system
结合图5同时参考主机液压系统管路布置,选择液压库中的对应元件从而搭建包含动力及控制系统的整机AMESim仿真模型,见图6。
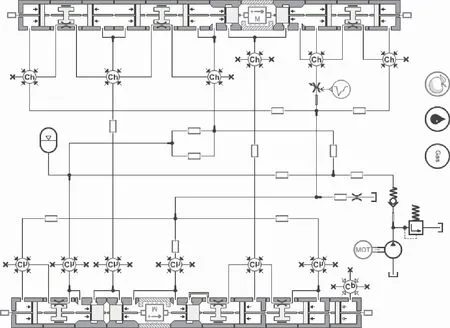
图6 整机AMESim仿真模型Fig.6 AMESim simulation model of whole machine
需要说明的是:图6中下部为活塞AMESim模型,上部为阀芯AMESim模型,其余为内部油道及供液系统对应的模型;内部流道中容积变化较大的容腔全部采用可变容积元件来表征;为了模拟回油背压,在换向阀回油侧及系统回油通道分别添加了可变及固定阻尼孔。
根据以上分析,结合碎石器结构参数及工作参数,列出整机仿真模型的主要参数,见表1。
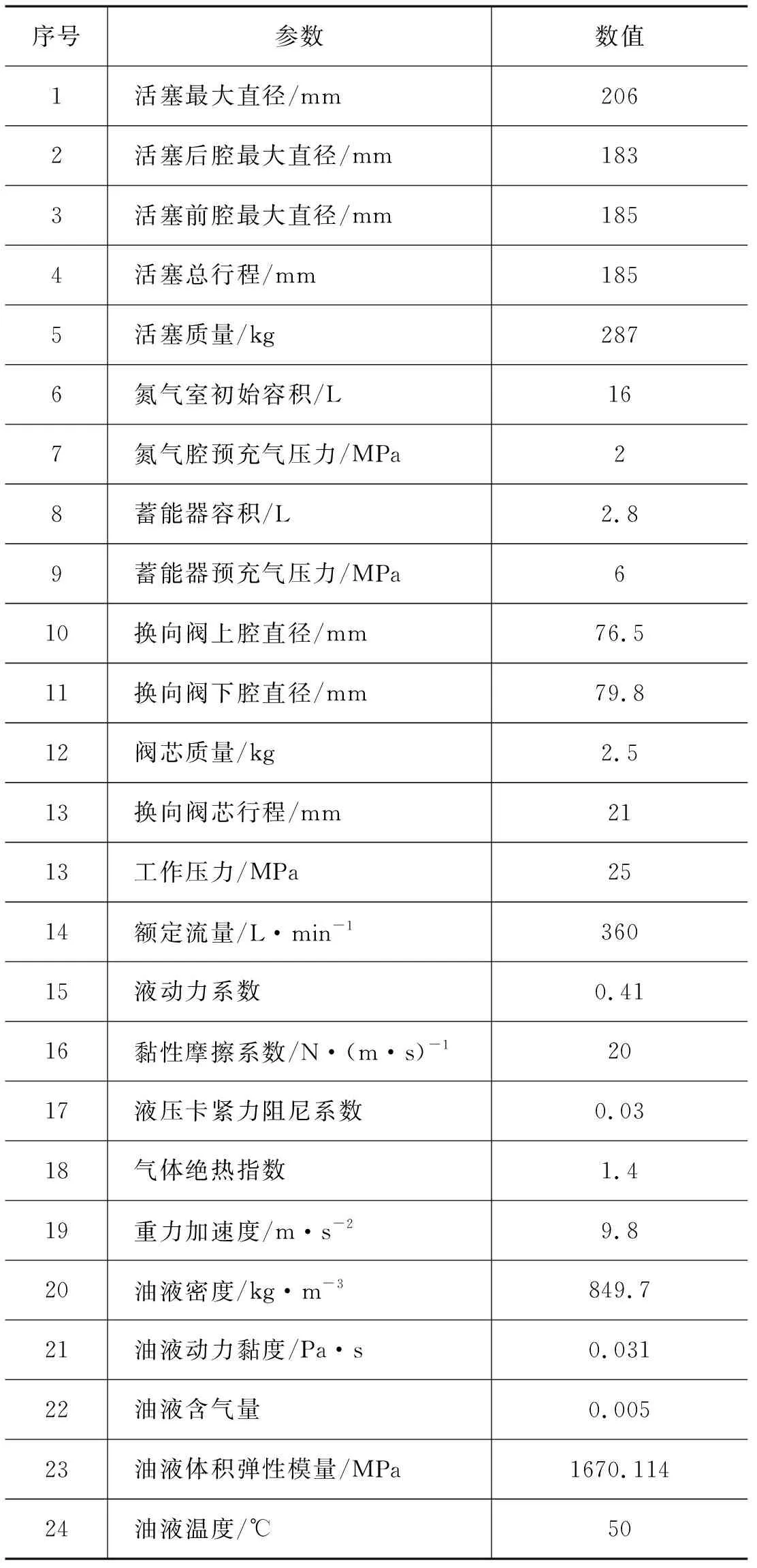
表1 整机仿真模型主要参数Tab.1 Main parameters of whole machine simulation model
2.4 正交试验设计
正交试验方法是利用正交表科学地安排与分析多因素的研究手段。该方法主要包括试验目标选择、因子-水平表确定、正交试验方案设计以及试验结果统计分析等步骤。
1) 因子-水平表
影响碎石器内部气穴现象的因素有工况参数及结构参数等,其为多因子、多水平的实际条件。因此确定可变的因子为:工作压力A、蓄能器压力B、氮气室初始容积C及活塞质量D等4个,同时假定A的水平取值分别为:25,27,29 MPa;B的水平取值分别为:5.0,6.5,8.0 MPa;C的水平取值分别为:13,16,19 L;D的水平取值分别为:280,290,300 kg。这样,将所考察的因子和水平列成如表2所示的形式。
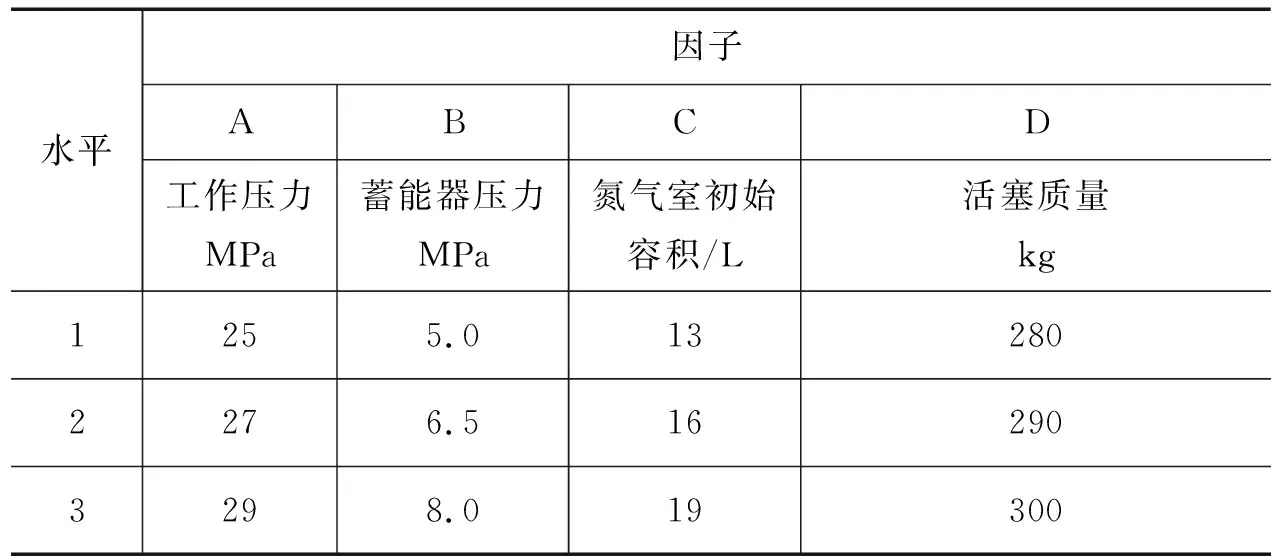
表2 正交试验因子水平表Tab.2 Orthogonal test factor level table
2) 正交试验方案
由表2可知,需要设计一个4因子、3水平的等水平正交表L9(34)。这样,可得9个具体的试验条件,对应的试验方案见表3。

表3 L9(34)正交试验方案Tab.3 L9(34) Orthogonal test scheme
3 计算结果与分析
3.1 活塞后腔瞬时压力分析
由文献[12]可知,碎石器冲程打击钎杆时由于补液不足造成活塞后腔出现气穴现象。根据前文正交试验方案,在AMESim平台中设定相应变量,同时设置仿真时间(10 s)与步长(0.0001 s),最后运行仿真。待计算完成后获取4.0~4.5 s之间不同试验对应活塞后腔瞬时压力psh,见图7。
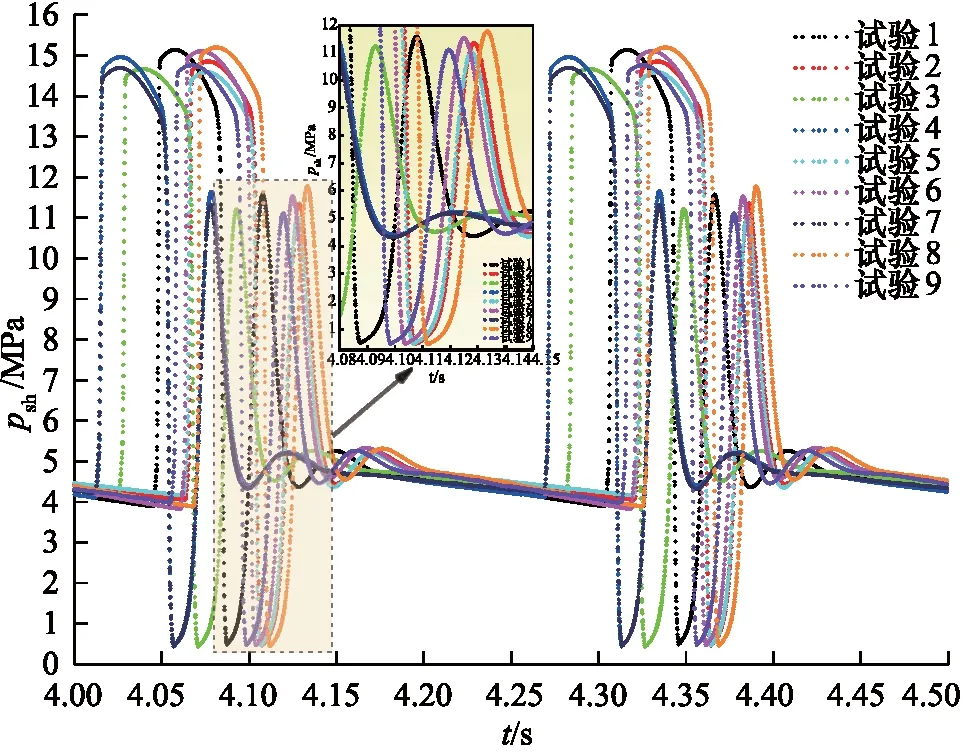
图7 不同试验条件下活塞后腔瞬时压力曲线对比Fig.7 Comparison of instantaneous pressure curves of piston rear cavity under different test conditions
由图7可知,不同试验对应瞬时压力曲线呈连续周期性变化,变化周期非常接近,大约为0.25 s。活塞运动至下死点时后腔压力最小,之后在回弹力的作用下活塞加速回程,后腔油液快速积累,出现了压力脉冲。随后在液压力与气压力的共同作用下活塞缓慢减速回程,对应的后腔压力浮动很小,此过程一直持续到后腔与常高压腔沟通。此后,由于高压油急速进入后腔,使得活塞瞬间降速,很快达到上死点,同时后腔压力迅速升高。
活塞冲程开始后,随着运动速度的不断加快,后腔压力快速递减,此过程一直持续到活塞到达下死点时,压力降至最低。此后一直循环这样的过程。
为进一步分析因子对活塞后腔最低压力影响程度,同时根据平均压力高低确定最优水平组合,获取不同试验对应最低压力正交试验分析表,见表4。
由极差法可知,表4中影响最低压力的各因子主次关系为:D>C>B>A,即活塞质量是主要因子,其次为氮气室初始容积,蓄能器压力与工作压力对最低压力的影响可忽略。随着活塞质量及氮气室初始容积地增加,后腔最低压力都不断降低。究其原因是活塞质量越低,相同工作条件下的运动速度越快,与阀芯速度的匹配程度越高;氮气室初始容积越小,其中氮气压力变化越大,对活塞的做功越多。
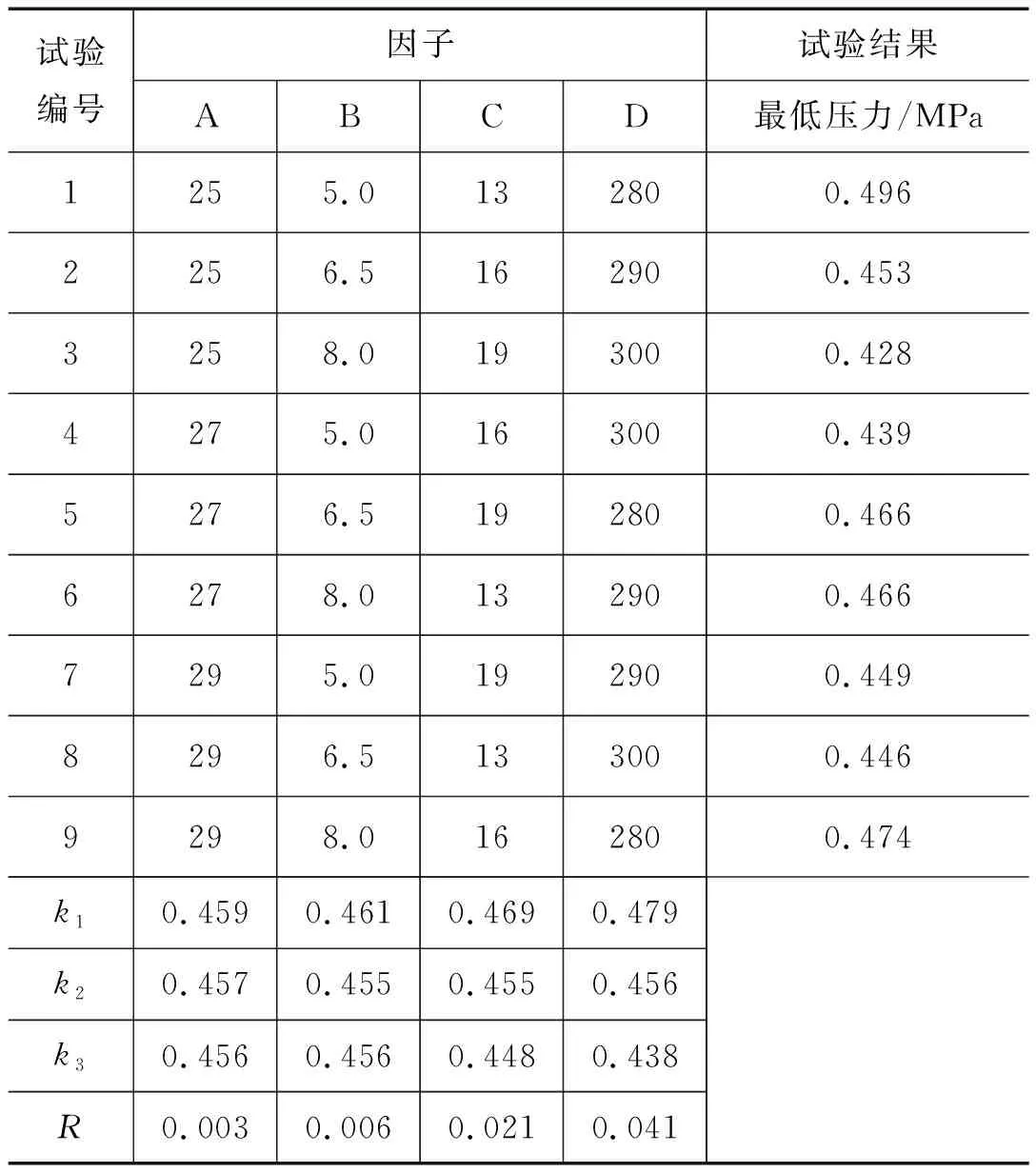
表4 活塞后腔最低压力正交试验分析表Tab.4 Orthogonal test analysis table of minimum pressure in the piston rear cavity
3.2 活塞打击速度分析
活塞打击速度直接影响着碎石器的工作能力,提高打击速度对于增加冲击能意义重大。因此,在AMESim仿真结果中获取4.0~4.5 s之间不同试验对应活塞速度Vp,见图8。
由图8可知,与瞬时压力曲线一致,不同试验对应速度曲线也呈连续周期性变化。活塞以最大速度打击钎杆后速度瞬间减为零,随后立即反向加速运动。由于此时活塞后腔压力很低,回程速度很快达到了最大值。然而,由于回油阻尼作用,结合图7可知,活塞后腔压力迅速升高,活塞很快减速,之后以幅值很小的波动速度回程,此过程一直持续到速度减为0。此后,在后腔高压油及氮气压力的共同作用下加速冲程,一直加速到以最大速度打击钎杆,之后一直重复这样的过程。
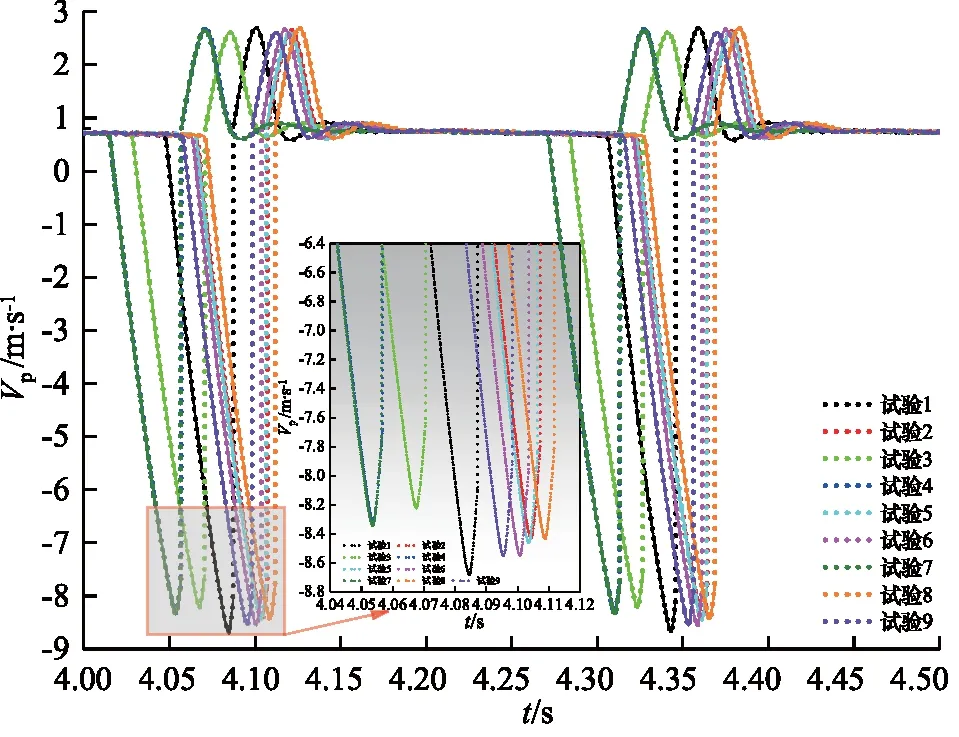
图8 不同试验条件下活塞速度曲线对比Fig.8 Comparison of piston speed curves under different test conditions
为进一步分析因子对活塞冲程最大速度的影响程度,同时根据平均最大速度的高低确定最优水平组合,获取不同试验对应冲程最大速度正交试验分析表,见表5。

表5 活塞冲程最大速度正交试验分析表Tab.5 Orthogonal test analysis table of maximum speed of piston stroke
由极差法可知,表5中影响冲程最大速度的各因子主次关系为:D>C>B>A,即活塞质量是主要因子,其次为氮气室初始容积,蓄能器压力与工作压力对最大速度的影响可忽略。随着活塞质量及氮气室初始容积地增加,冲程最大速度都不断减小,其原因与影响后腔最低压力类似。
4 结论
(1) 因子及对应水平组合对活塞运动周期的基本无影响,不同试验对应的周期都为0.25 s左右;
(2) 活塞质量与氮气室初始容积是影响活塞后腔最低压力与冲程最大速度的主要因子。为了增加后腔最低压力同时提高打击速度,必须采用质量更小的活塞及容积更小的氮气腔;
(3) 以最大速度打击钎杆后由于回弹力作用,活塞并未经历停顿,而是立刻加速回程,直至活塞后腔出现压力脉冲后才开始以幅值很小的波动速度减速回程。
