基于NSGA-Ⅱ光热光伏耦合冷热电联供系统优化

赵丹丹， 江代君， 徐今朝， 王登文， 王 军

(1. 东南大学 能源与环境学院， 南京 210096； 2. 中国电建集团华东勘测设计研究院有限公司，杭州 311122； 3. 南京帕偌特太阳能有限公司， 南京 211106)

由于传统化石能源的不可再生性和环境污染性，为有效解决能源供需不平衡和环境保护等问题，需要更高的能源利用率和更大的可再生能源占比。以近用户侧及能源梯级利用为特点的分布式能源系统，可以同时满足用户的冷、热、电等多种需求，实现对一次能源的高效利用，减少环境污染物的排放，因此受到了世界各国广泛的重视并得到了发展[1-2]。近年来，有专家学者提出将太阳能[3]、风能[4]、地热能[5]等清洁能源与分布式能源系统进行耦合，通过在一次侧引入可再生能源，减少化石燃料的使用和环境污染物的排放。

异质能源的大规模耦合，将会导致系统往往无法同时兼顾经济性和能源性(耦合系统相比于传统能源系统，在一次能源消耗方面具有的优势)，因此优化耦合系统的容量配置和运行策略成为在进行多能互补分布式能源系统设计时的另一个重要课题[1]。在这个过程中，各类智能优化算法为该问题提供了有效的解决方案。在各类智能优化算法中，遗传算法由于在冷热电联供系统优化中具有优异的全局搜索性被广泛采用，大多数研究直接采用遗传算法或以遗传算法为基础通过耦合其他方法构建系统求解模型[6]，并取得了优异的成果。

基于目前分布式可再生能源系统结合太阳能发展的现状，笔者提出了一种光热光伏耦合冷热电联供系统，并利用带精英保留策略的快速非支配排序遗传算法(NSGA-Ⅱ)，以费用年值节约率、一次能源节约率和二氧化碳减排率为优化目标对耦合系统进行优化。

1 系统建模

1.1 系统组成及运行策略

光热光伏耦合冷热电联供系统可划分为光伏子系统、槽式集热储热子系统和末端用能设备3个部分。图1为该系统的能量流动示意图。

图1 光热光伏耦合冷热电联供系统的能量流动示意图

1.2 各子模块建模

1.2.1 光伏发电模型

光伏电池输出功率的计算公式[7]为：

(1)

式中：EPV为光伏电池输出功率；Estc为光伏电池在标准测试工况下的输出功率；S、Sstc分别为实际工况和标准测试工况下的太阳辐照度；t、tstc分别为实际工况和标准测试工况下的环境温度；ε为光伏电池的温度衰减系数。

1.2.2 槽式集热储热模型

(1) 集热模型。

基于聚光器和集热管的能量平衡搭建集热管稳态传热模型，即建立聚光器接收的有效太阳辐射量与聚光器和集热管的光学损失、集热管的热损失及管内传热工质的热增量之间的能量守恒模型[8-9]。具体计算公式为：

Qloss=Qgo_a,conv+Qgo_a,rad

(2)

Qenv+Qgi_go,cond=Qgo_a,conv+Qgo_a,rad

(3)

Qgi_go,cond=Qao_gi,conv+Qao_gi,rad

(4)

Qabs=Qao_gi,conv+Qao_gi,rad+Qao_ai,cond

(5)

Qao_ai,cond=Qai_f,conv

(6)

式中：Qloss为集热管热损失；Qenv为玻璃套管吸收的太阳辐射传热量；Qabs为吸热管吸收的太阳辐射传热量；Qgo_a,conv为玻璃套管外表面与环境的对流传热量；Qgo_a,rad为玻璃套管外表面与环境的辐射传热量；Qgi_go,cond为玻璃套管内外壁面的导热传热量；Qao_gi,conv为吸热管外壁面与玻璃套管内壁面的对流传热量；Qao_gi,rad为吸热管外壁面与玻璃套管内壁面的辐射传热量；Qao_ai,cond为吸热管内外壁面的导热传热量；Qai_f,conv为吸热管内壁面与传热流体之间的对流传热量。

忽略管道热损失，则槽式集热系统输出热量为：

QPTC=Qai_f,conv

(7)

式中：QPTC为槽式集热系统输出热量。

集热器热效率[10]为：

(8)

式中：ηth为集热器热效率；Aa为集热器开口面积；θ为太阳入射角。

(2) 储热模型。

采用双罐显热蓄热，为简化模型计算，假设罐内温度保持一致并忽略储热系统热损失。储热系统各时刻可提供的热量为：

Qstorage=Mcp,oil(Toil,hot-Toil,cold)

(9)

式中：Qstorage为储热系统各时刻可提供的热量；M为储热油的质量；cp,oil为储热油的比定压热容；Toil,hot为热罐储热油的温度；Toil,cold为冷罐储热油的温度。

1.3 耦合系统建模

在上文各子模块建模的基础上，基于能量守恒搭建了耦合系统仿真模型。

电平衡公式为：

Ehybrid,e+EPV=Qe+Ehybrid,c+Ehybrid,h

(10)

式中：Ehybrid,e为电网购电量；Ehybrid,c为冷水机组耗电量；Ehybrid,h为电锅炉用电量；Qe为末端用户电负荷。

热平衡公式为：

QPTC+Qstorage+QPV+Qboiler=

(Qh+Qabsorb)/ηex

(11)

Qboiler=Ehybrid,hηb

(12)

式中：Qboiler为电锅炉输出热量；QPV为光伏多余电能经电转热装置转换得到的热量；Qh为末端用户热负荷；Qabsorb为溴化锂机组耗热量；ηex为换热器效率；ηb为电锅炉效率。

冷平衡公式为：

Qabsorb,out+Qchiller,out=Qc

(13)

Qabsorb,out=Qabsorbξabs

(14)

Qchiller,out=Ehybrid,cξc

(15)

式中：Qc为末端用户冷负荷；Qabsorb,out为溴化锂机组供冷量；Qchiller,out为冷水机组供冷量；ξabs为溴化锂机组能效；ξc为冷水机组能效。

耦合系统购电量为：

Ehybrid=Ehybrid,e+Ehybrid,c+Ehybrid,h

(16)

式中：Ehybrid为耦合系统购电量。

耦合系统的一次能源消耗量及二氧化碳排放量为：

Fhybrid=ξcoal,gridEhybrid

(17)

eCO2,hybrid=λCO2,gridEhybrid

(18)

式中：Fhybrid为耦合系统一次能源消耗量；eCO2,hybrid为耦合系统二氧化碳排放质量；ξcoal,grid为电网购电的折算标准煤系数；λCO2,grid为电网购电的二氧化碳排放系数。

1.4 模型验证

在太阳能驱动的冷热电联供系统中，光热及光伏组件模型的准确性对系统的研究具有非常重要的意义。在本文中，光伏组件的发电模型主要采用经验公式[7]，为验证光热组件模型的准确性，从集热器的集热性能及聚光效率进行验证。

在辐照度、环境温度等初始条件相同的情况下，将仿真结果与文献[11]中的实验结果进行对比，结果见表1，其中：ta为环境温度；va为环境风速；tf为传热流体进口温度；qV,f为传热流体体积流量。由表1可得：传热流体出口温度的计算值和实验值的相对误差在2%以内，满足模型准确性的要求。

表1 LS-2槽式集热器仿真结果与实验结果的对比

图2为LS-3槽式集热器全年聚光效率仿真结果与文献结果[12]的对比。

图2 LS-3槽式集热器全年聚光效率仿真结果与文献结果的对比

由图2可得：所搭建模型的仿真结果与文献结果的趋势基本一致，两者聚光效率的相对误差小于3%。通过仿真所得到的集热器最大光学效率为74.84%，与文献[13]中的77%相比，相差2.16百分点。这主要是因为本文中集热器的截获因子为0.884 4，而文献中集热器的截获因子为0.930 0，集热器全年聚光效率的仿真结果在误差允许范围内，验证了所搭建模型的准确性。

2 多目标优化

2.1 NSGA-Ⅱ构建

NSGA-Ⅱ是基于非支配排序遗传算法(NSGA)的改进算法[14]，通过引入快速非支配排序和精英保留策略，在保障种群多样性的同时迅速提高了种群个体的适应度水平，提升了算法的优化效率。NSGA-Ⅱ基本参数的取值见表2。

表2 NSGA-Ⅱ基本参数的取值

2.1.1 决策变量

将光伏组件数目NPV、槽式集热器数目NPTC和储热罐体积Vstorage(单位为m3)作为多目标优化的决策变量。各决策变量的搜索范围为：

(19)

2.1.2 目标函数

从经济、能源、环境方面评估联供系统性能，所采用的目标函数分别为费用年值节约率、一次能源节约率和二氧化碳减排率，其计算公式分别为：

(20)

(21)

(22)

式中：RAC为费用年值节约率；RPE为一次能源节约率；RCDE为二氧化碳减排率；C为系统年度总投资；F为系统一次能源消耗量，在本文中主要是指电网端一次侧化石能源消耗量，而太阳能作为一种可再生能源，不计入该项；eCO2为系统二氧化碳排放量；N为系统总运行时间，取8 760 h；j为系统各运行时间节点；下标ref、hybrid分别表示参照系统、耦合系统。

在参照系统中，用户的冷热电负荷分别由冷水机组、电锅炉和电网提供，相应的购电量、一次侧能源消耗量和二氧化碳排放量的计算公式分别为：

Eref=Eref,e+Eref,c+Eref,h

(23)

Eref,c=Qc/ξc

(24)

Eref,h=Qh/ηb

(25)

Fref=ξcoal,gridEref

(26)

eCO2,ref=λCO2,gridEref

(27)

式中：E为购电量；下标c、h、e分别代表冷、热、电。

经济性参数取值见表3[15-18]。

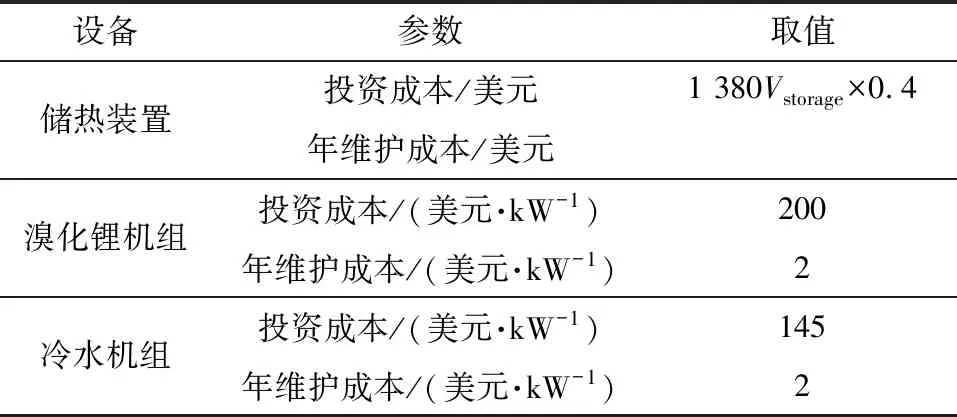
表3(续)

2.1.3 约束条件

耦合系统及参照系统的约束条件主要包括：(1)设备单元最大装机容量约束；(2)系统能量守恒及质量守恒约束；(3)运行策略约束；(4)设备输入输出特性约束。

2.2 场景选取

以上海某办公楼作为研究对象，将当地逐时气象数据和冷热电负荷数据载入耦合系统及参照系统，利用NSGA-Ⅱ进行多目标优化。所用的气象数据及负荷数据均由DeST软件导出。

2.3 结果分析

2.3.1 优化结果

图3为耦合系统多目标优化结果。图3中的曲线是由一系列满足目标条件的不差解(Pareto 最优解)组成的Pareto前沿曲线，曲线上的各点均为可以实现更好的耦合系统性能的可行方案。耦合系统的经济性与能源和环境效益之间存在相互冲突的现象，系统经济性能的提升伴随着能源和环境效益的下降。当系统的一次能源节约率从8.84%变化至35.81%时，费用年值节约率从9.37%变化至-59.77%，系统经济性大幅下降。由于耦合系统仅以电网电能作为辅助能源，并且未将太阳能计入一次能源消耗，因此在优化结果中耦合系统的一次能源节约率和二氧化碳减排率呈线性相关。

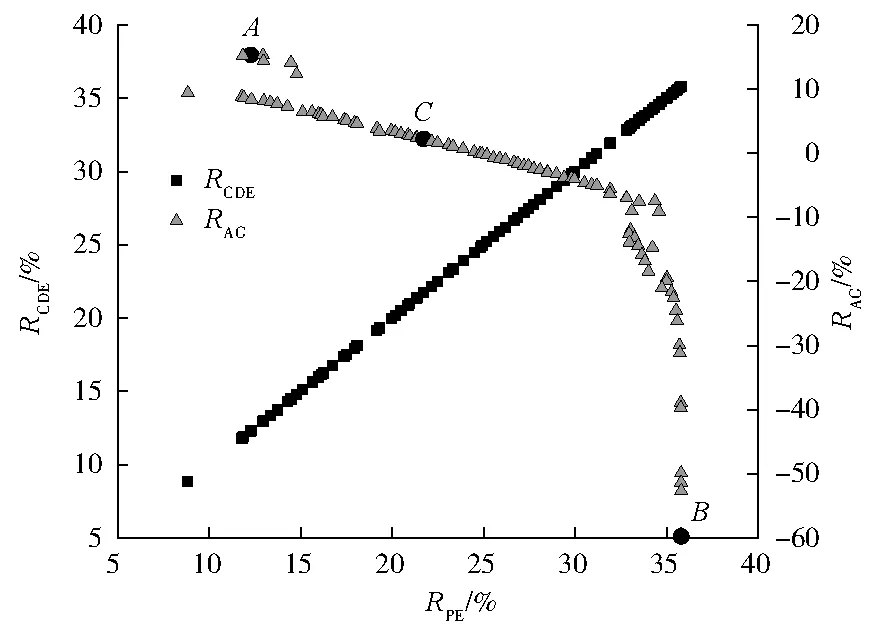
图3 耦合系统多目标优化结果

图3中A、B、C点分别代表最佳经济性能点、最佳能源性能点(主要是指耦合系统的一次能源节约率)和在具有一定经济性优势时所能得到的最优能源性能点。A、B、C点对应的耦合系统优化结果见表4。影响系统经济性能的最主要因素为设备初投资，当槽式集热储热系统及光伏系统的装机容量较小时，系统的经济性能较好，但同时为满足末端负荷需求，电网端的购电量较高，系统的能源和环境效益较差；当仅考虑系统一次能源节约率和环境性能时，如在B点，系统配备了最大的槽式集热储热系统及光伏系统的装机容量，以使系统能在最大程度上减少电网端的购电量。将以C点作为案例分析点，对耦合系统的系统性能和运行情况进行分析。

表4 A、B、C点对应的耦合系统优化结果

表5为耦合系统C点与参照系统的性能对比。由表5可得：耦合系统C点与参照系统的初投资相差不大，耦合系统的初投资比参照系统高约3.98%，其年运维成本却是参照系统的6倍左右。这主要是因为槽式系统的维护成本较高，约占整个系统年运维成本的83%。由于引入太阳能作为系统的一次侧能源输入，耦合系统的运行成本大大减少，这部分节约的费用弥补了耦合系统和参照系统在系统初投资和年运维成本上的差距，使耦合系统在保证能源性能的同时实现较好的经济效益。

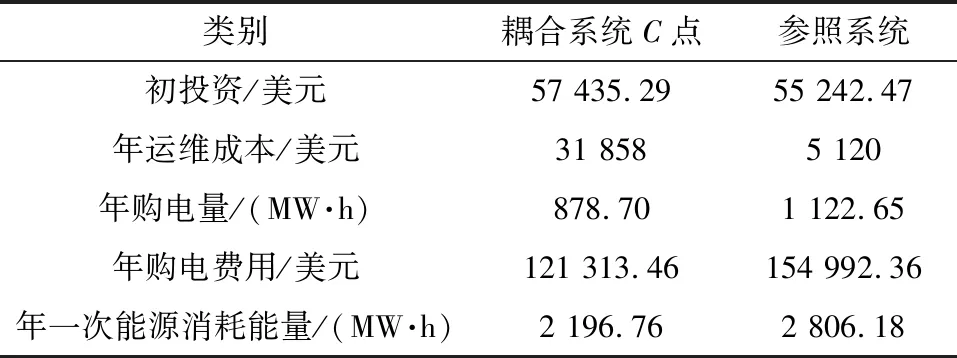
表5 耦合系统C点与参照系统的性能对比

2.3.2 敏感性分析

由于太阳能的间歇性，在太阳能不能满足用户侧需求时，耦合系统需要从电网购电，因此电网电价将直接影响系统的经济性。以C点为案例分析点，研究电价波动对耦合系统经济性能的影响，电价变化率选取-50%～+50%。图4为电价波动对耦合系统经济性的影响。由图4可得：电价波动时耦合系统的经济性变化较大，当电价变化率从-50%上升至+50%时，耦合系统的费用年值节约率由-8.78%上升至7.37%，即电价变化率平均每增加10百分点，费用年值节约率上升1.61百分点。

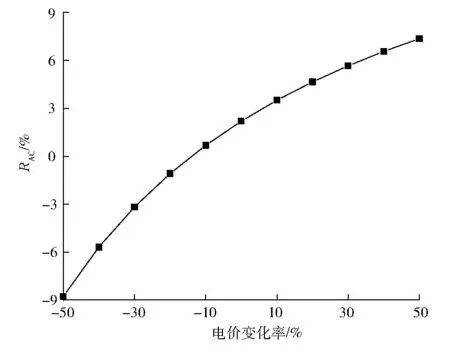
图4 电价波动对耦合系统经济性能的影响

3 结语

基于分布式可再生能源系统和太阳能发展的现状，提出了一种光热光伏耦合冷热电联供系统。以上海某办公楼的全年逐时冷热电负荷分析为案例，利用NSGA-Ⅱ，以系统费用年值节约率、一次能源节约率和二氧化碳减排率为优化目标，对耦合系统进行配置优化，得出的主要结论为：

(1) 对比参照系统，所提出的耦合系统具有更好的能源和环境效益，通过在一次侧引入太阳能，大大减少了化石能源的消耗，优化后的耦合系统一次能源节约率最低为8.84%、最高为35.81%。

(2) 由于槽式集热器和光伏电池等装置的使用，耦合系统的初投资及维护成本要远远高于参照系统，但是相应的电网购电量大幅减少，系统运行成本较低，耦合系统的经济性优势也得到体现。

(3) 对耦合系统进行敏感性分析，电价波动会对系统的经济性产生较大影响，电价变化率平均每增加10百分点，费用年值节约率上升1.61百分点。

组件配置优化对于耦合系统设计来说至关重要，通过对耦合系统中各组件配置进行优化，可以使其在保证较高能源和环境效益的同时实现一定的经济效益，对今后可再生能源的发展具有重要意义。