拉瓦尔式气态燃料调节阀控制系统仿真及阀门流动分析
2022-09-20刘婷婷张一岑余海彬戴义平
刘婷婷, 张一岑, 余海彬, 戴义平
(西安交通大学 能源与动力工程学院,西安 710049)
目前,常用的燃气流量控制策略为泵控和阀控2种方式。泵控系统结构复杂、成本高、动态响应较差,而阀控系统结构简单、成本低、动态响应速度快,因此在燃气轮机燃料阀组的控制方案中采用阀控方式比较合理[1]。
液压伺服阀采用液体压差驱动主控制元件,具有控制精度高、能够实现闭环控制等特点,在仪器仪表中得到了广泛的应用。ZHENG F X等[2]提出了一种基于力矩马达的插装式2D电液伺服阀,并探索了该阀的动态特性,开环模型的仿真结果表明:支撑压力对2D电液伺服阀动态特性影响不大,该模型具有良好的动态特性。陈祖希[3]针对动压反馈时间常数的传统求解方法进行了误差分析,给出了动压反馈时间常数的数值求解方法;提出了实现同步测试时间常数和反馈流量增益的新方案。肖占林[4]通过3D实体建模和动力学仿真,得到了执行机构不同弹簧刚度、活塞面积和力臂对输出特性的影响,并对弹簧和液压缸进行了设计优化,提高了执行机构的工作稳定性,延长了执行机构的工作寿命。KIM H G等[5]提出了一种力导数补偿和自然速度反馈的力控制方法,提出了将其应用于实际系统的思路。YANG H等[6]对连续微型射流对挡板-喷嘴先导阀的操纵装置进行了数值研究,结果表明:连续微型射流的作用大大削弱了挡板-喷嘴的空化现象。AUNG N Z等[7-8]提出一种简单有效的挡板形状, 利用菱形喷嘴代替传统的圆形喷嘴,从而减少喷嘴-挡板空化对阀门稳定性的影响。王书铭等[9]探究了结构参数对射流偏转板电液伺服阀动态作用的机理。
李洪洲等[10-12]采用有限元分析方法,分析了气态燃料的速度和压力分布,结果表明:在不改变阀芯位移和进口压力的条件下,流经阀口的燃料流量保持不变,并且与出口压力无关。张亮[13]在阀芯位移闭环控制条件下对主阀阀口开闭特性、正弦响应特性,以及控制压力对控制特性的影响进行了分析,得出阀芯位移闭环的控制特性。孟爱红[14]对汽车电子稳定控制(ESC)系统液压执行机构进行了系统研究,提出了拓宽高速开关线性控制范围的方法,实现了对轮缸压力的精确控制。
拉瓦尔式调节阀是基于拉瓦尔管气体动力学原理设计,具有精确流量调节作用的一种新型阀门,采用液压伺服阀控制拉瓦尔式阀门的开度。为了确定拉瓦尔式调节阀的响应特性,建立了拉瓦尔式调节阀及其液压控制系统的仿真模型,在MATLAB仿真环境下对其动态响应特性进行了仿真分析,利用FLUENT软件对拉瓦尔式调节阀流动特性进行了数字模拟,以期为液压伺服阀控制拉瓦尔式阀门的设计提供理论基础。
1 液压伺服控制系统组成
液压伺服控制系统由伺服放大器、伺服阀、液压缸、主阀和位移传感器组成(见图1)。
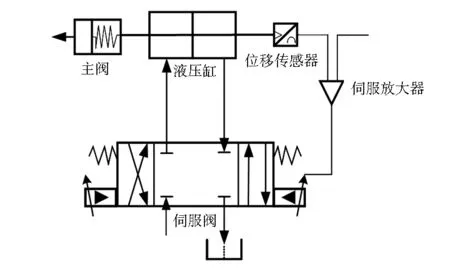
图1 液压伺服控制系统
控制液压缸的活塞位移可以控制主阀阀芯位移。位移传感器将活塞位移转换为电压信号,电压信号与输入电压信号比较,得到偏差电压。偏差电压经伺服放大器放大后成为电流信号,电流信号驱动电液伺服阀将液压油输出到液压缸,使得液压缸2个腔室产生压差,推动活塞运动,进而带动主阀阀芯运动。随着液压缸活塞的运动,腔室两侧压差逐渐减小;当液压缸腔室两侧油压相等时,活塞停止运动,主阀开度达到指定位置后停止运动。
2 液压伺服控制系统模型
2.1 伺服放大器模型
将伺服放大器与力矩马达线圈的传递函数看作惯性环节,其表达式为:
(1)
式中:Ka为伺服放大器与线圈电路增益,A/V;ωa为线圈转折频率,rad/s;I为伺服阀输入电流,A;Ue为偏差电压,V;s为传递函数的变量。
2.2 伺服阀模型
当伺服阀的固有频率为100 Hz以上时,将其考虑为惯性环节,传递函数为:
(2)
式中:Gsv(s)为伺服阀的传递函数;Ksv为伺服阀以电流为输入、空载流量为输出时的流量增益,m2/s;Tsv为惯性环节的时间常数。
2.3 液压缸模型
采用双向液压缸,液压缸输出位移相对阀输入位移的传递函数为:
(3)
式中:Gp(s)为液压缸的传递函数;ωh为液压缸固有频率,rad/s;Kqx为液压缸流量增益,m2/s;Ap为液压缸活塞面积,m2;ξh为液压缸阻尼比,一般为0.1~0.2。
2.4 主阀模型
主阀采用拉瓦尔式调节阀,其结构见图2[12]。

图2 主阀结构
主阀阀口为拉瓦尔管结构形式;拉瓦尔管的结构主要包括进口、稳定段、收缩段、喉部和扩张段;进气口设置在靠近出口端的位置。
稳定段为拉瓦尔管前端,长度为L0,它的主要作用是降低紊流度,使进入拉瓦尔管的气流更加稳定和均匀。
收缩段通过加速气流,使得出口气流平直且稳定均匀。收缩段宜选择较短的长度,但不能太短,太短会对喉部及收缩段进口气流产生扰动,增大总压损失。尤其是进口处的气流会产生大的逆压梯度,导致附面层分离,无法得到稳定的气流。
喉部为亚声速到超声速变化的阶段。
扩张段的扩张角太大容易引起射流扩散太快,出口处产生的激波比较严重,对阀的稳定工作产生一定影响;扩张角太小引起的压力损失大,因为此时气体超声速段变长,并且扩张段太长会导致结构尺寸太长,从而浪费材料。
拉瓦尔管临界状态下的气体质量流量为:
(4)

当气体流速达到声速时,热流系数为:
(5)
式中:γ为比热容比,空气约为1.4;R为气体常数,空气约为287 J/(kg·K)。
喉部临界面积为:
At=πx(dt-xsinα·cosα)sinα
(6)
式中:dt为主阀阀口喉部直径,m;α为半锥角角度,(°);x为阀芯位移,m。
主阀阀芯在运动时所受的力分为周缘力、侧向力和轴向力。在实际加工中,阀芯台肩上设计周向均压槽,槽内液体压力处处相等,起径向平衡作用,基本可以消除周缘力和侧向力,因此阀设计中不计算液压周缘力和侧向力。阀芯在轴向受到的力主要有惯性力、弹性力、驱动力、黏性阻力、液动力。液动力又分为稳态液动力和瞬态液动力:稳态液动力是指在阀口开度一定的情况下,液流对阀芯的反作用力;瞬态液动力是指在阀芯运动过程中,阀口开度变化使通过阀口的流量发生变化,引起阀腔内液流速度随时间变化,其动量变化对阀芯产生的反作用力。
惯性力是阀芯在运动时,因速度变化而产生的阻碍阀芯运动的力。在分析阀芯静态特性时不考虑惯性力,动态分析时再考虑。
与弹簧相接触的阀芯所受到的弹性力FT为:
FT=k(x0±x)
(7)
式中:k为弹簧刚度,N/m;x0为弹簧预压缩量,m。
阀芯受到的稳态液动力F为:
F=ρqV(v1-v2cosβ)+p1A1+F1sinθ-
(8)
式中:ρ为气体密度,kg/m3;qV为气体体积流量,m3/s;v1为主阀出口气流速度,m/s;v2为主阀进口气流速度,m/s;β为气流入射角,(°);A1为主阀出口过流截面积,m2;p1为出口压力,Pa;F1为阀座对气体燃料的力,N;θ为阀座锥面半锥角,(°);L为阀芯圆锥母线,m;ds为阀芯圆锥底面直径,m;p2为阀腔内压力,Pa。
阀芯受到的瞬态液动力Ft为:
(9)
式中:t为时间,s。
3 液压伺服控制系统仿真
设计液压缸内径为80 mm,液压活塞杆的最大行程为75 mm,液压油的体积弹性模量为700 MPa,液压阻尼比取0.15。
图3为液压伺服控制系统的仿真结果。输入幅值为5的正弦位置信号,负载干扰力为1 500 N,幅值为600 N,频率为1.5 Hz。

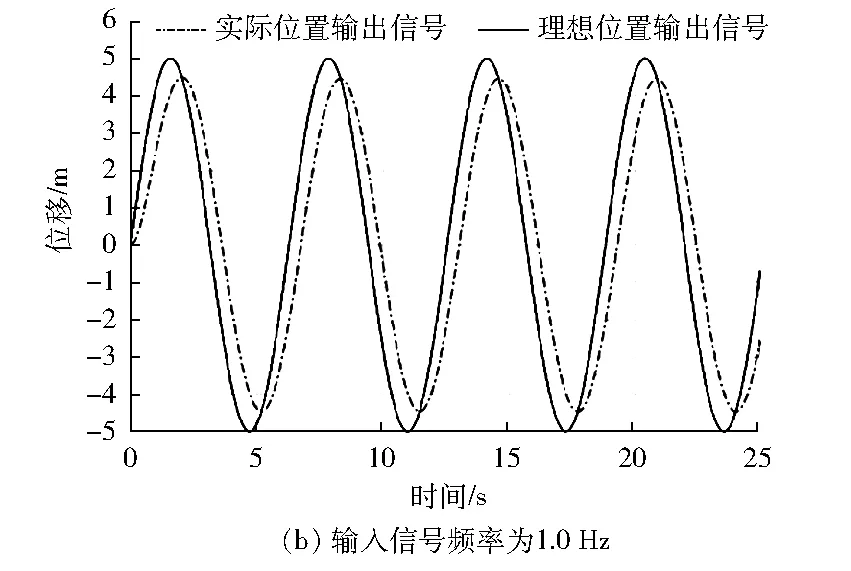
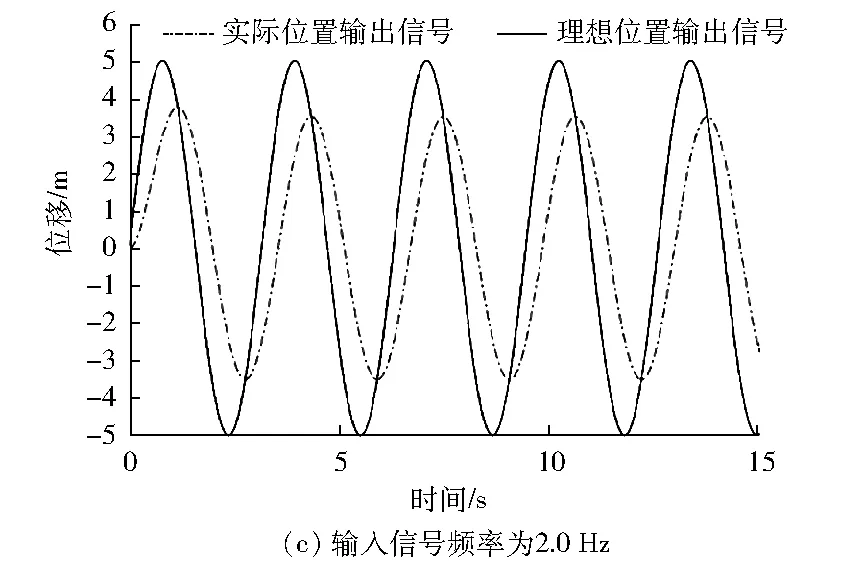
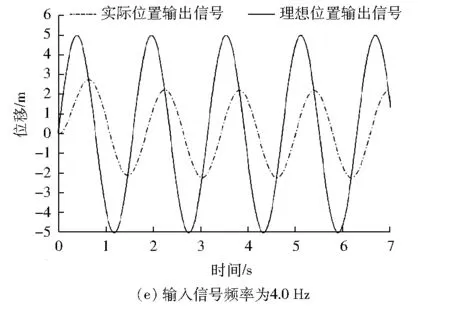
从图3可以看出:随着位置输入信号频率的增大,实际输出信号的幅值衰减增大,相位滞后增加。频率为1 Hz以下时,系统动态品质良好,响应速度很快,衰减幅值较小,相位滞后小,系统能够很好地跟随输入信号的变化。
4 拉瓦尔式调节阀阀口流场分析
采用ANSYS网格划分工具划分网格,边界条件及计算分析在FLUENT软件中进行,求解器采用隐式、分离、稳态格式;压力速度耦合使用SIMPKEC算法;动量压力设定为高阶迎风格式。湍动能及湍耗散采用收敛的k-ε模型,中心面SYMMRITRT设置,进口条件如下:阀口进口总压为4 MPa,进口静压为3.99 MPa,出口静压为0.1~3.9 MPa,进口湍流强度为6%,进口湍流直径为7 mm,出口回流流强度为5%,出口回流湍流直径为6 mm。拉瓦尔式调节阀网格划分结果见图4。
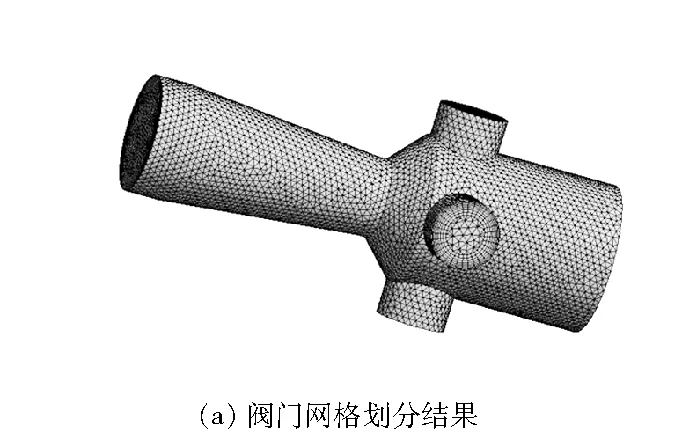
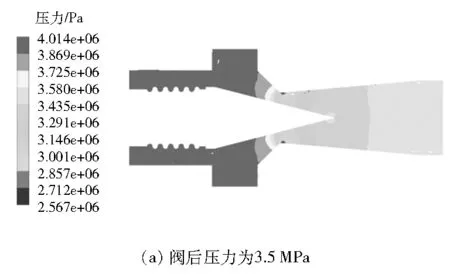
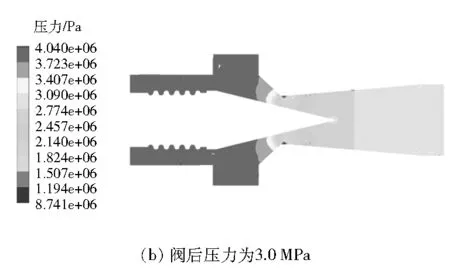
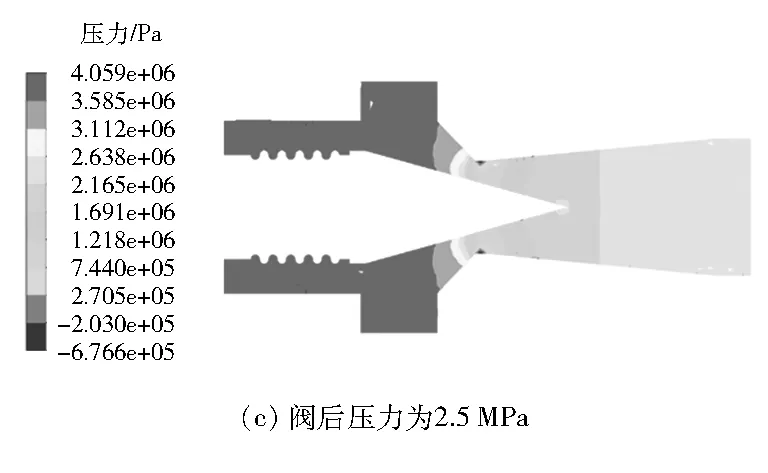
图5为不同阀后压力下阀口的压力分布图。由于拉瓦尔式调节阀的特殊结构,阀口的压力先变小后变大,在喉部达到最小压力;阀后压力小于3 MPa时,喉部射流出现了负压,在扩张段压力恢复到一定水平。由于在阀内消耗了一部分动能,气态燃料压力在出口处未能恢复到进口压力。
图6为不同阀后压力下的流线分布图。


从图6可以看出:气态燃料进入调节阀时,流速增大,由于阀芯喉部面积小于进口节流口面积,所以流过喉部时流速进一步增大,并且在喉部最窄处流速达到最大,燃气从该处射流后容易冲击壁面,动能转化为内能,使得高速气态燃料的流速下降。在波纹管的弯曲结构处容易形成漩涡,但是由于此处燃料流速很小,能量损失很小。
5 结语
通过对燃料阀组液压控制系统进行仿真,得出了该控制系统的动态特性,并利用FLUENT软件对拉瓦尔式调节阀流动特性进行仿真分析,得出如下结论:
(1) 从液压伺服控制系统的仿真结果可以看出,随着位置输入信号频率的增大,实际输出信号的幅值衰减增大,相位滞后增加。该液压伺服控制系统在输入信号频率低于1 Hz时具有良好的动态响应特性。
(2) 从拉瓦尔式调节阀阀口的压力分布图可以看出:阀口的压力先变小后变大,在喉部达到最小;阀后压力小于3 MPa时,喉部射流出现了负压,然后在扩张段压力恢复到一定水平。
(3) 从拉瓦尔式调节阀阀口的流线分布图可以看出,气态燃料进入调节阀时,流速增大,由于阀芯喉部面积小于进口节流口面积,所以流过喉部时流速进一步增大,并且在喉部最窄处达到最大,随后逐渐恢复,但未能达到进口速度。
