基于 ADAMS 液压重载机械臂定位偏差的修正方法

郝兵，申浩翰，杨柳松，王富勇，胡同海，黄涛

1中信重工机械股份有限公司 河南洛阳 471039

2洛阳矿山机械工程设计研究院有限责任公司 河南洛阳 471039

3矿山重型装备国家重点实验室 河南洛阳 471039

随着现代工业的快速发展，矿山设备逐渐趋于大型化，对大型设备的维护保养及辅助生产提出了更高的要求[1-2]。重载机械臂因有助于提高大负载作业工作效率，降低作业难度和人工成本[3]，在矿山领域得到了广泛的应用。国内外学者对重载机械臂定位精度进行了大量的研究工作，取得了较大的进展。文献 [4-8] 通过对机械臂各系统进行研究，为机械臂的设计提供了参考。文献 [9-11] 通过对机械臂的工作过程进行动力学和运动学分析，优化了机械臂的机电液控制策略。文献 [12-16] 通过逆运动学求解，给出了多关节机械臂和其他机械结构的最优运动参数。

以上研究为重载机械臂的设计、控制和运动参数等方面提供了大量参考。但是逆运动学求解方法在提高机械臂定位精度方面的应用仍缺乏研究。因此，笔者以液压重载机械臂的配合间隙为研究对象，通过逆运动求解的方法，对减小或消除机械臂定位偏差展开了研究。

1 配合间隙对定位偏差的影响

在利用逆运动学求解方法对机械臂末端定位偏差进行修正前，需要对配合间隙引起的定位偏差进行了解。

1.1 液压重载机械臂虚拟样机

ADAMS 具有强大的运动学和动力学仿真能力，但是其对模型的处理能力较差。因此，需要将机械臂模型处理后，以Parasolid 格式导入 ADAMS 中建立虚拟样机。导入后的液压重载机械臂虚拟样机如图 1所示。其中一、二、三段机械臂的颜色由浅到深，将其分别称为内臂、中臂和外臂，最大有效工作半径为 2.5 m。底座和地面之间、液压构件和其他零件之间均为转动副，液压缸和液压杆之间为圆柱副，各臂节之间则通过双边接触函数来约束其自由度。载荷为30 kN，位置在机械臂内臂最前端，方向为y轴负方向。

图1 液压重载机械臂虚拟样机Fig.1 Virtual prototype of hydraulic heavy-load robotic arm

1.2 双边接触函数的确定

根据图 1 中各臂节间的几何关系，即可确定关键点的位置。结合双边接触函数建立方法[17]，将关键点和各点编号进行匹配，如表 1 所列。

表1 机械臂上关键点的编号位置Tab.1 Number and location of key points on robotic arm

确定了各关键点的编号信息，即可确定各关键点的双边接触函数。由于各臂节间与液压缸为转动副连接，因此各臂节间在y方向无转动自由度，在z方向无平移自由度，故此处仅确定y方向的双边接触函数即可。

内臂关键点B1在y方向的双边接触函数为

BISTOP(DY(85，87，87)，VY(85，87，87，87)，-1，1，1e8，1.5，1e3，1e-10)；

内臂关键点C1在y方向的双边接触函数为

BISTOP(DY(84，96，96)，VY(84，96，96，96)，-1-(2/DX(96，85，85))*DX (84，96，96)，1 +(2/DX(96，85，85))*DX (84，96，96)，1e8，1.5，1e3，1e-10)；

中臂关键点B2在y方向的双边接触函数为

BISTOP(DY (87，89，89)，VY(87，89，89，89)，-1，1，1e8，1.5，1e3，1e-10)；

中臂关键点C2在y方向的双边接触函数为

BISTOP(DY(86，88，88)，VY(86，88，88，88)，-1-(2/DX (88，87，87))*DX(86，88，88)，1 +(2/DX (88，87，87))*DX(86，88，88)，1e8，1.5，1e3，1e-10)。

1.3 机械臂末端的定位偏差

载荷和约束添加完毕后，就需要对机械臂的运动过程进行设定：首先将连接内臂、中臂和外臂的 2 个液压缸分别伸出 900 mm，外臂和底座间的液压缸收缩 50 mm，来模拟机械臂的抓取过程；然后将外臂和底座间的液压缸伸出 250 mm，在底座绕y轴正方向转动 30°后收缩 250 mm，来模拟放置物体的过程；最后将内臂、中臂和外臂间的液压缸复位，外臂和底座间的液压缸复位，底座绕y轴转动复位至初始状态。各运动过程的宏观表现及所对应的系统时间如表2 所列。

表2 机械臂运动设定Tab.2 Motion setting of robotic arm

取械臂末端编号为 105 的关键点A1作为计算定位偏差的基准点，将关键点A1在含配合间隙和理想样机中的x、y、z方向运动轨迹对比，可得定位偏差如图 2 所示。

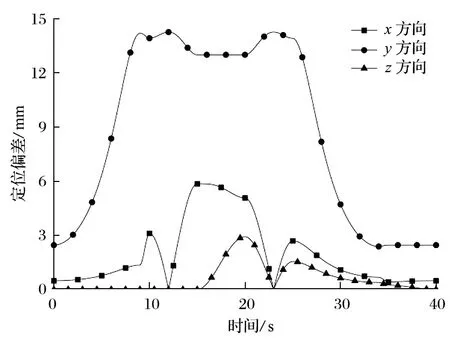
图2 含配合间隙的机械臂定位偏差Fig.2 Positioning deviation of robotic arm with fitting clearance

由图 2 可以看出，随着机械臂的伸出、俯仰和转动，x、y、z方向上定位偏差的变化趋势并无固定规律，其中y方向即载荷方向的偏差量远高于其他 2 个方向，最大值为 14.28 mm，因此可以认为由配合间隙引起的机械臂末端定位偏差较大，且很难找到固定的变化规律。

2 ADAMS 逆运动学求解

在ADAMS 中，可以通过一般点驱动 (General Point Motion) 约束定位基准点的运动形式，再对其他自由构件添加必要的约束和载荷，来反算机械臂各关节和液压缸的工作参数。

2.1 机械臂末端的运动轨迹

在约束定位基准点的运动轨迹之前，需要先确定该基准点理想状况下的运动轨迹。将理想样机中关键点A1在x、y、z方向上的运动轨迹分别导出，如图 3所示。

图3 定位基准点的理想运动轨迹Fig.3 Ideal motion trajectory of positioning reference point

2.2 仿真参数设定

获取了定位基准点的运动轨迹后，就是对原有的载荷和约束进行调整。

首先建立基准点的运动轨迹约束。将基准点x、y、z方向的运动轨迹以样条曲线的形式导入ADAMS，x方向运动轨迹如图 4 所示，通过 Cubic Fitting Method (CUBSPL) 三次样条插值函数对各方向上运动轨迹的样条曲线进行插值，再与关键点A1处添加的一般点驱动的x、y、z方向平移约束建立关联，如图 5 所示。

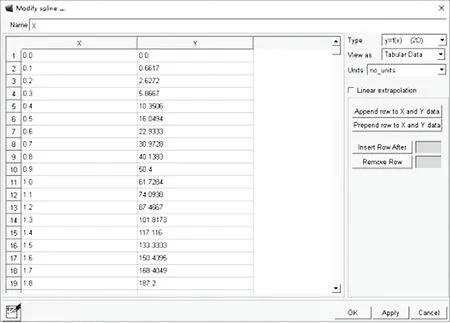
图4 定位基准点 x 方向运动轨迹Fig.4 Motion trajectory of positioning reference point along direction x

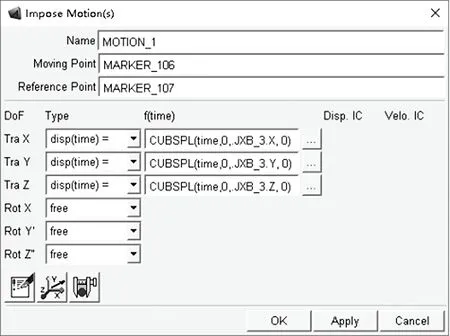
图5 关键点 A1 的一般点驱动Fig.5 General point motion of key point A1

其次是对于载荷的调整。由于原载荷位置已添加一般点驱动作为支承，使该载荷相较于正运动学计算时无法产生对应的力矩，进而无法对机械臂各臂节间的几何关系产生影响。故将机械臂末端 30 kN 的载荷由力矩替代，施加于关键点A1，以确保各臂节间的几何关系符合间隙配合的理论。

最后是对于约束的调整，由于原约束中臂节间液压缸的伸缩量并无直接关系，但原驱动中定义了液压缸有着相同的伸缩量。如果在逆运动学求解的过程中不对其伸缩量添加关联，则机械臂在伸出和收缩的过程中，中臂会出现较为明显的轴向震动。因此，对臂节间的两液压缸伸缩量进行等量约束。

2.3 液压缸的行程修正

进行逆运动学仿真计算后，即可导出各液压缸进行修正后的运行参数。修正后的运行参数与原运行参数进行对比，变幅液压缸和臂节间液压缸的行程修正量如图 6 所示。由图 6 可以看出，变幅杆液压缸和臂节液压缸较初始的行程参数均做出了伸出补偿，机械臂整体呈上扬的拱形状态来修正载荷方向的定位偏差。其中变幅杆液压缸修正量的最大值为 1.63 mm，远大于臂节液压缸修正量的最大值 0.11 mm，且两者的变化趋势均与正运算时y轴偏差量的变化趋势相近。由于机械臂不存在z方向摆动的可能，因此底座的运行参数无需修正。

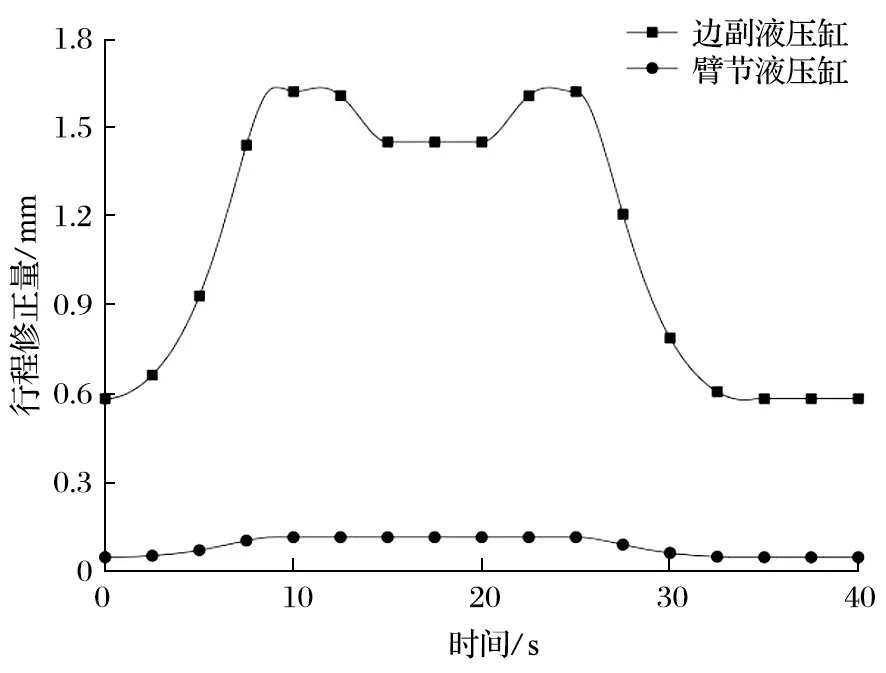
图6 液压缸的行程修正Fig.6 Stroke correction of hydraulic cylinder

3 定位偏差的修正效果

将各液压缸修正前的运行参数替换为修正后的运行参数，导入含配合间隙的液压重载机械臂虚拟样机中，重新计算机械臂末端定位偏差，即可检验ADAMS 的逆运动学求解在消除机械臂定位偏差方面的有效性。

3.1 修正后的液压缸行程参数导入

将各液压缸修正后的运行参数以样条曲线的方式导入 ADAMS，以变幅杆液压缸为例，如图 7 所示。再通过三次样条插值函数对样条曲线进行插值，最后将其与各液压缸的驱动参数相关联，以变幅杆液压缸为例，如图 8 所示。

图7 变幅液压缸行程参数Fig.7 Stroke parameter of variable-amplitude hydraulic cylinder

图8 变幅液压缸驱动Fig.8 Drive with variable-amplitude hydraulic cylinder

3.2 修正后机械臂末端的定位偏差

以修正后的运行参数作为驱动，代入含配合间隙的机械臂虚拟样机中，记录其定位基准点x、y、z方向的运动轨迹。再将该运动轨迹与理想样机中定位基准点运动轨迹进行对比，其偏差如图 9 所示。由图 9可以看出，通过逆运动学求解来消除机械臂末端定位偏差的效果非常明显，原定位偏差中，x、y、z方向的最大值分别为 5.86、14.28、2.93 mm，修正后的定位偏差最大值仅为 0.010 4 mm，可以认为在虚拟样机中，由配合间隙引起的机械臂末端定位偏差已经基本消除。

图9 逆运动学修正后机械臂的定位偏差Fig.9 Positioning deviation of robotic arm after inverse kinematic correction

4 结论

利用 ADAMS 提供的逆运动学求解方法，对含配合间隙的伸缩式液压重载机械臂进行正运动学和逆运动学求解，开展减小机械臂末端定位偏差的方法研究，结论如下。

(1) 对于最大有效工作半径为 2.5 m 的液压重载机械臂而言，当机械臂臂展达到最大值时，臂节间 2 mm 的配合间隙会引起机械臂末端在载荷方向上最大14.28 mm 的定位偏差。

(2) 通过 ADAMS 的逆运动学求解，可以得出各驱动修正后的运行参数，与原样机中驱动的运行参数相比，变幅杆补偿最大值为 1.63 mm，臂节液压缸补偿最大值为 0.11 mm。

(3) 将各驱动修正后的运行参数导入含配合间隙的机械臂虚拟样机中进行运动学求解，与理想样机中机械臂末端定位基准点运动轨迹进行对比，定位偏差最大值仅为 0.010 4 mm。可以认为逆运动学求解方法对于减少或消除配合间隙在机械臂上引起的末端定位偏差效果显著。