悬臂式掘进机截割部系统建模及仿真研究

彭天好，何兴川，储安圆

(安徽理工大学机械工程学院，安徽淮南 232001)

0 前言

悬臂式掘进机作为煤矿井下综掘面的主要设备，其自动截割技术的发展是提高煤矿巷道断面成型质量，实现煤矿巷道快速掘进的基础。而掘进机截割头位置控制的重点在于截割部回转与升降角度的控制。悬臂式掘进机截割部的回转与升降均是以单个电液比例阀控制两个液压缸的方式驱动。目前针对阀控液压缸系统的理论建模方法主要有两种：一种是通过建立传递函数的方法进行建模；另一种是采用建立非线性模型的方法，但都是以阀控单液压缸系统作为研究对象，这与悬臂式掘进机的实际液压系统和机械系统情况并不一致。本文作者分析了截割部回转与升降部分阀控双缸液压系统的压力、流量特性，结合对截割部机械系统的运动学和动力学分析，建立了截割部系统非线性数学模型。并在MATLAB/Simulink环境构建了截割部系统仿真模型，对掘进机典型截割工况下的截割部回转及升降角度进行了闭环控制仿真分析。

1 掘进机截割部工作原理

图1为掘进机截割部结构示意。回转液压缸一侧伸出、另一侧缩回驱动回转台，带动悬臂水平摆动，构成回转系统；升降液压缸同步动作，驱动悬臂垂直升降，构成升降系统；两者共同控制悬臂运动，由截割头对巷道截面进行截割。截割头的精确定位取决于回转与升降角度，它们之间的运动学关系可通过建立D-H坐标系完成求解，限于篇幅，这部分内容文中不予讨论。

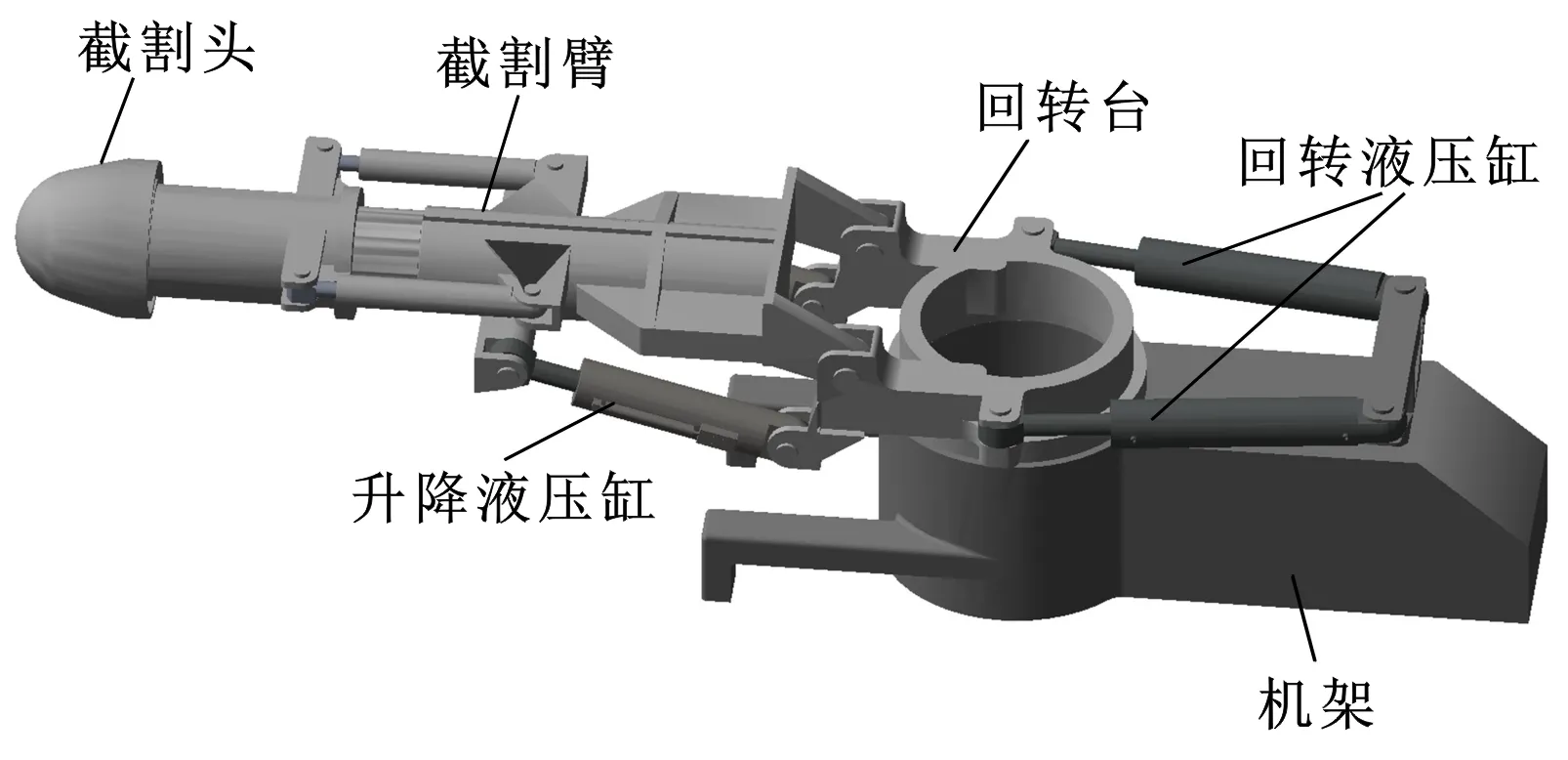
图1 悬臂式掘进机截割部结构示意

悬臂式掘进机截割部液压系统原理如图2所示，由负载敏感泵提供系统动力，可匹配系统工作压力和流量需求进行输出，采用电液比例阀控制液压缸动作。

图2 截割部液压系统原理

2 掘进机回转系统数学模型

2.1 电液比例阀传递函数

电液比例阀传递函数为

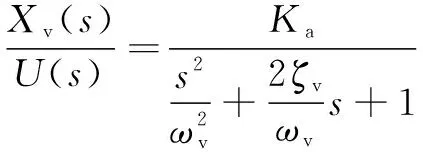
(1)

式中：()为阀芯位移；()为输入电压；为电液比例阀增益系数；为固有频率；为阻尼比。

2.2 回转机构液压系统数学模型

悬臂式掘进机截割部回转液压系统原理如图3所示，回转液压缸的缸体分别与机架铰接，活塞杆末端分别与回转台铰接，驱动回转台绕点转动。为便于数学建模，假设管道无流量、压力损失；比例阀为零开口四通对称滑阀；两液压缸结构相同，无油液外泄漏；油液温度和体积弹性模量为常数。

图3 回转机构液压系统原理

以图3所示运动方向为例，回转电液比例阀的流量方程为

(2)

式中：为阀口流量系数；为阀口面积梯度；为油液密度。

右回转液压缸两腔的流量连续性方程：

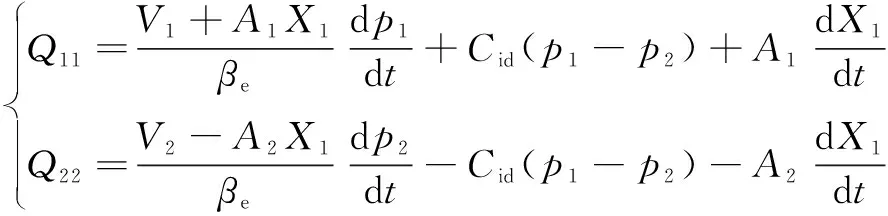
(3)

式中：为液压缸内泄漏系数；为体积弹性模量。

左回转液压缸的两腔流量连续性方程：

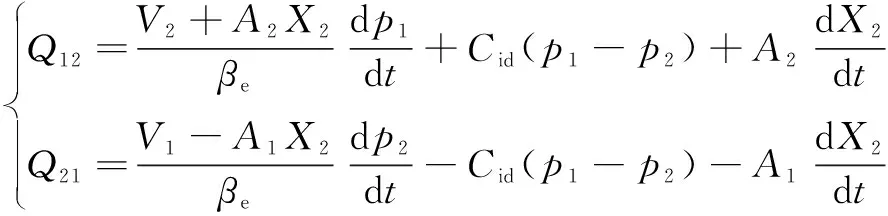
(4)

根据流量关系=+，=+，将式(3)、式(4)整理简化后可得：

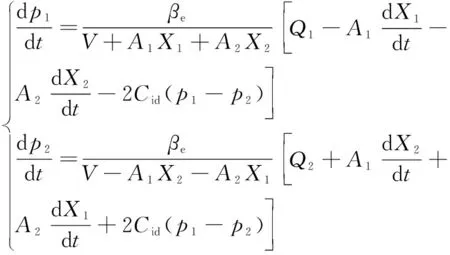
(5)

式中：为回转液压缸初始等效容积，=+。

对左右回转液压缸进行受力分析，可得回转液压缸的动力学方程：

(6)

式中：为回转液压缸活塞杆质量；为等效黏性阻尼系数；为弹簧刚度系数；和分别为右侧和左侧回转液压缸外负载。

2.3 回转机构数学模型

回转机构简化模型如图4所示。其中，点为回转台回转中心，、为液压缸与回转台铰接点，、为液压缸与掘进机机身铰接点，为中点。记：==，==′=′=，==，∠=∠=。设回转台向左转动角度为，则右侧液压缸活塞杆伸出位移为，左侧液压缸活塞杆缩回位移为。

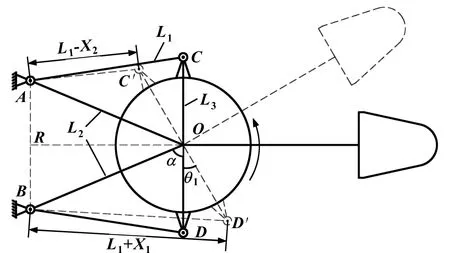
图4 回转机构简化模型

由余弦定理可得两侧回转液压缸活塞杆位移与回转台水平转动角度之间的关系：

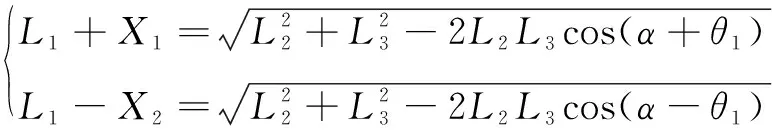
(7)

对上式两边取微分，可得回转液压缸位移速度和回转台水平转动角速度之间的关系：

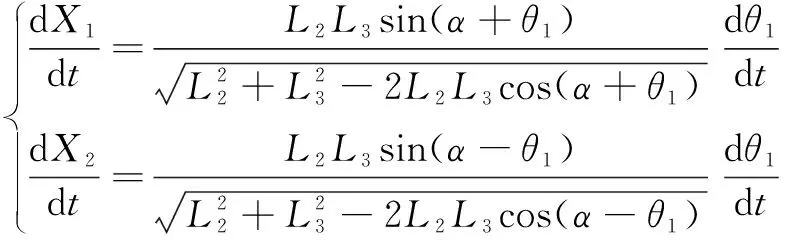
(8)

根据刚体定轴转动定律，可得回转机构的力矩平衡方程：

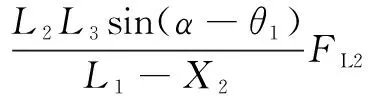
(9)

式中：为回转机构转动惯量；为回转负载转矩；为回转摩擦转矩。

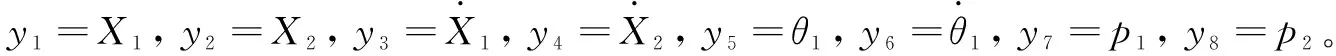
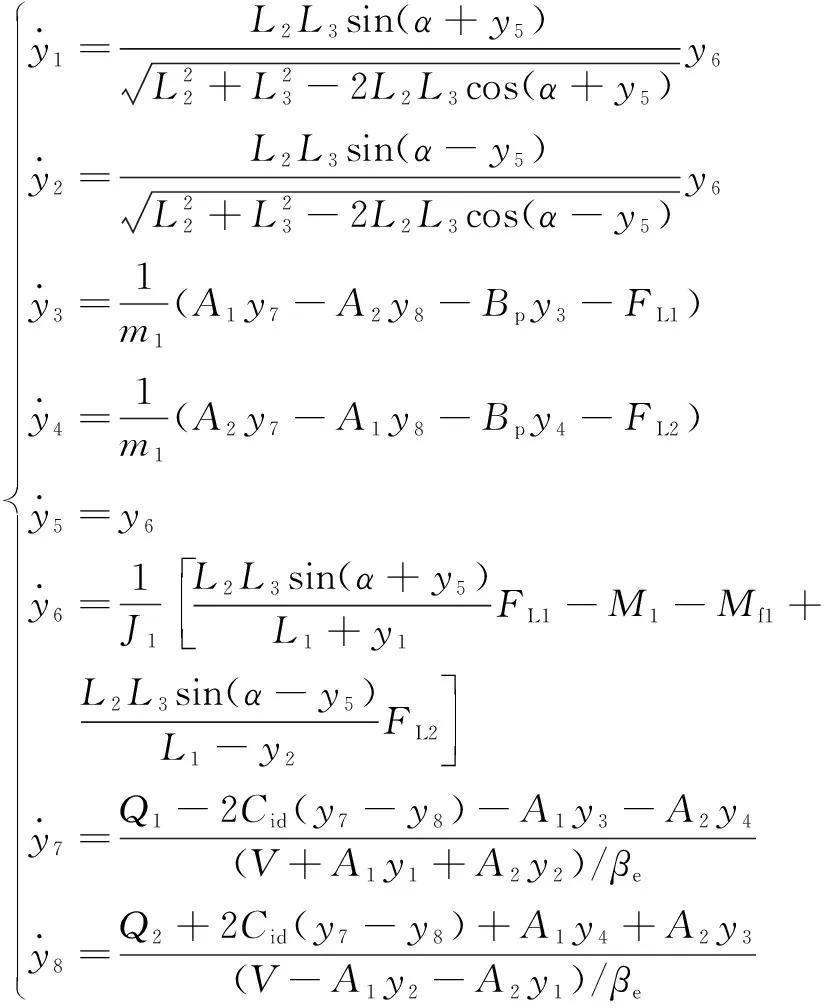
(10)

3 掘进机升降系统数学模型

3.1 升降液压系统数学模型

掘进机截割部升降机构液压系统原理如图5所示，左右两侧升降液压缸结构相同，且同步动作。

图5 升降机构液压系统原理

类似于回转机构液压系统分析过程，可得到升降电液比例阀的压力流量方程式(11)、升降液压缸的流量连续方程式(12)和动力学方程式(13)。

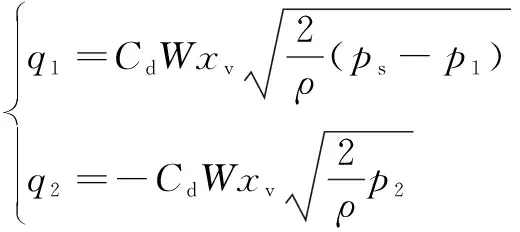
(11)

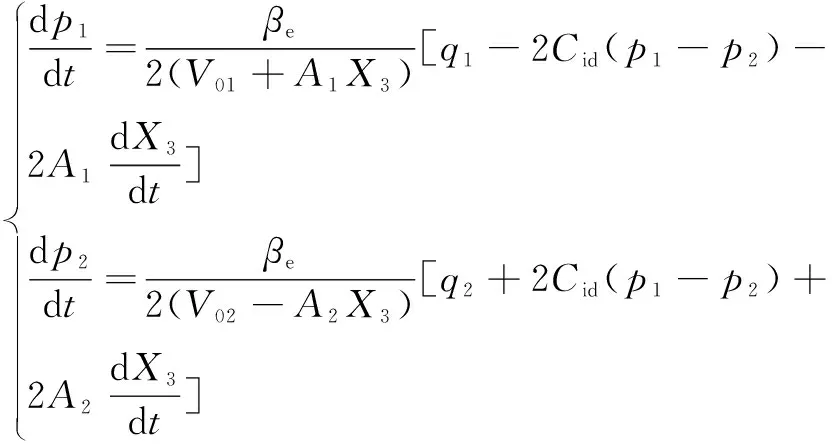
(12)

(13)

式中：为升降液压缸活塞杆质量；为升降液压缸外负载。

3.2 升降机构的数学模型

升降机构简化模型如图6所示。其中：为悬臂与回转台铰接点，为升降液压缸与回转台铰接点，为悬臂重心，为升降液压缸与悬臂铰接点。记：=，=，=，∠=，设悬臂上升角度为，升降液压缸活塞杆位移为。

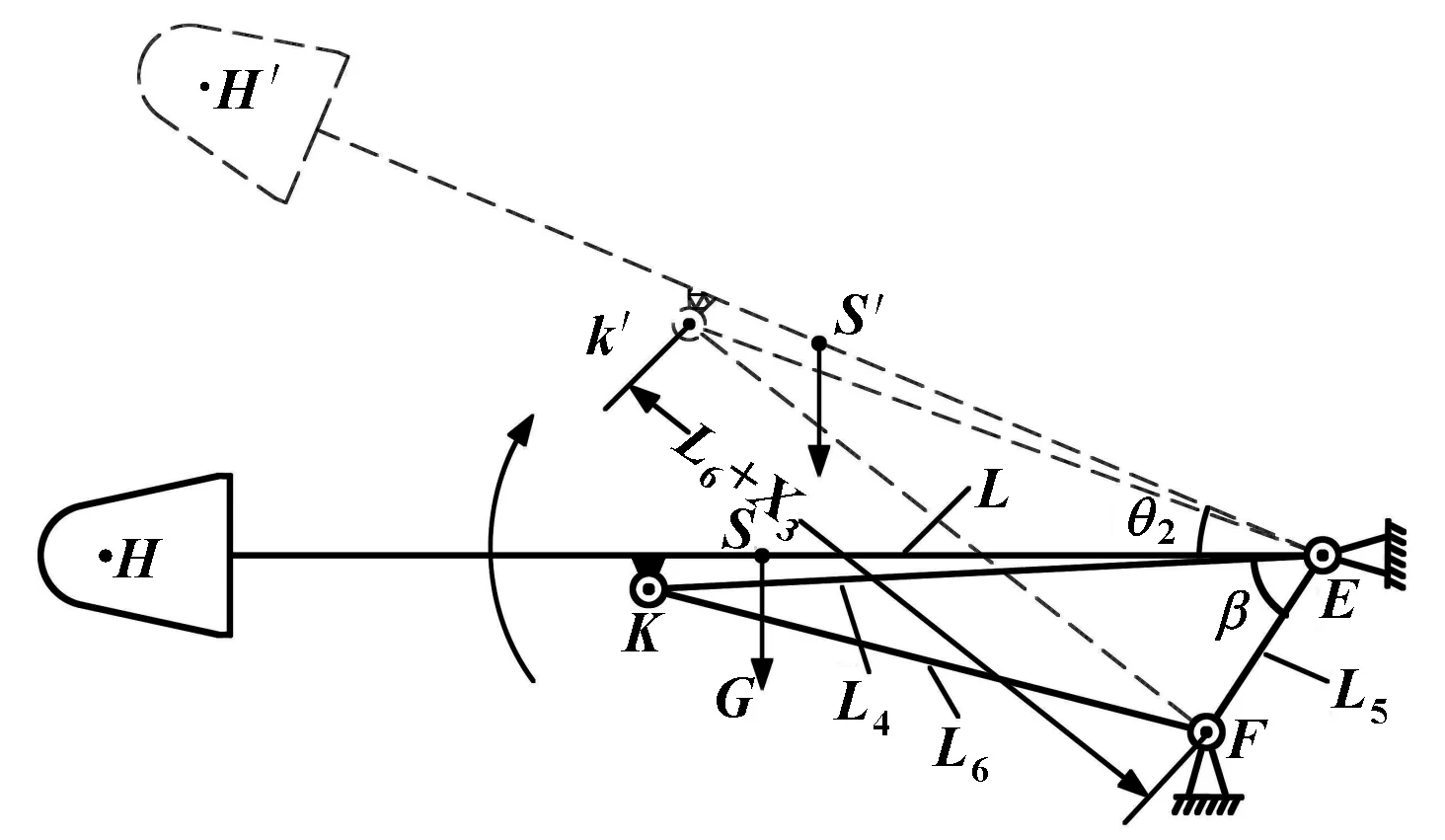
图6 升降机构简化模型

由余弦定理可得升降活塞杆位移速度和悬臂升降角速度之间的关系：

(14)

升降机构受重力产生的重力矩为=cos，则升降机构的力矩平衡方程：

(15)

式中：为升降机构转动惯量；为升降负载转矩；为升降摩擦转矩。

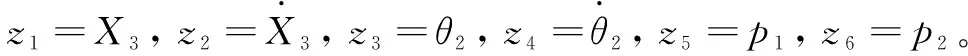
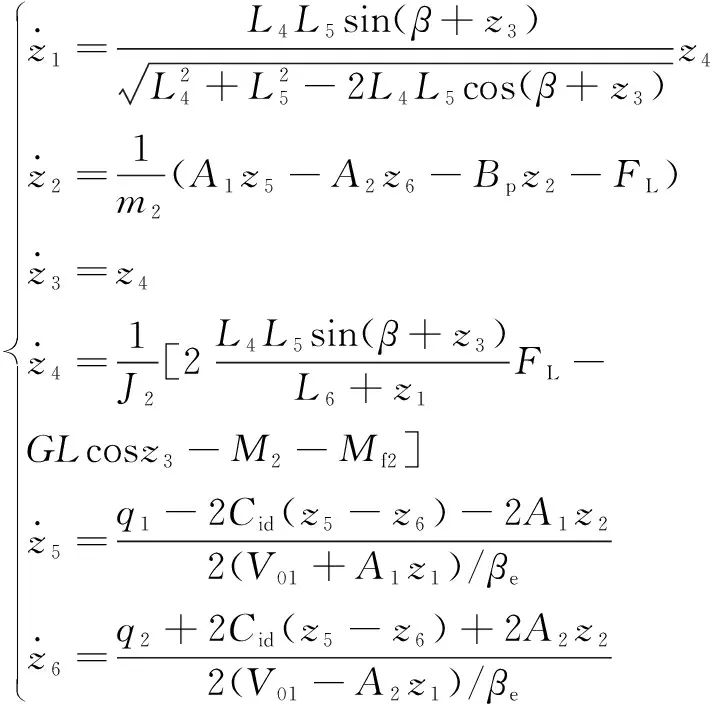
(16)

4 掘进机截割部系统模型与仿真分析

4.1 截割部系统仿真模型

由截割部回转与升降系统的非线性数学模型，在MATLAB/Simulink环境构建悬臂式掘进机截割部系统的仿真模型，如图7所示。

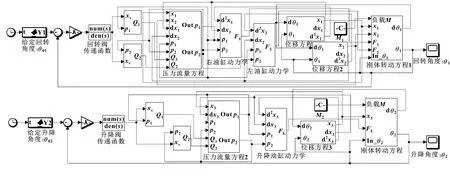
图7 掘进机截割部系统仿真模型

图7中，给定悬臂回转和上升的目标角度分别为和，与运行时反馈信号、作差值运算得到角度误差信号，经系数转换为电液比例阀的控制信号，再经电液比例阀的传递函数得到阀口位移信号。图中、为外负载转矩。掘进机参数设置如表1所示。

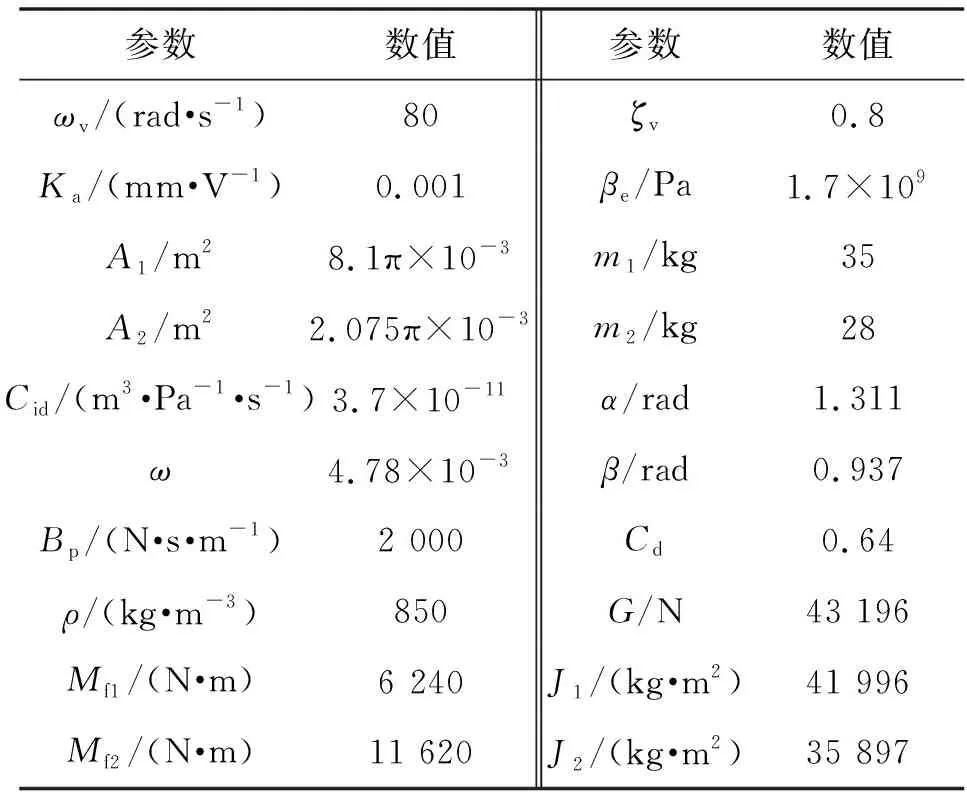
表1 悬臂式掘进机截割部系统参数

4.2 仿真结果与分析

按掘进机工况，对掘进机悬臂上升、左摆及右摆动作进行仿真。给定截割工况为：0～1 s内悬臂由0 rad上升到0.036 rad，1～4 s内悬臂由0 rad左转到0.15 rad，4～5 s内由0.036 rad上升到0.072 rad，5～8 s内由0.15 rad右转回到0 rad；0～1 s和4～5 s上升时负载转矩为137 460 N·m，1～4 s和5～8 s回转时负载转矩为253 780 N·m。

图8、图9分别是悬臂升降和回转的角度仿真曲线。可知：悬臂上升和回转时能很好地跟踪给定的目标角度，但由于系统的惯性，系统存在一定的滞后，悬臂上升时最大跟踪误差为0.004 3 rad，回转时为0.005 2 rad。

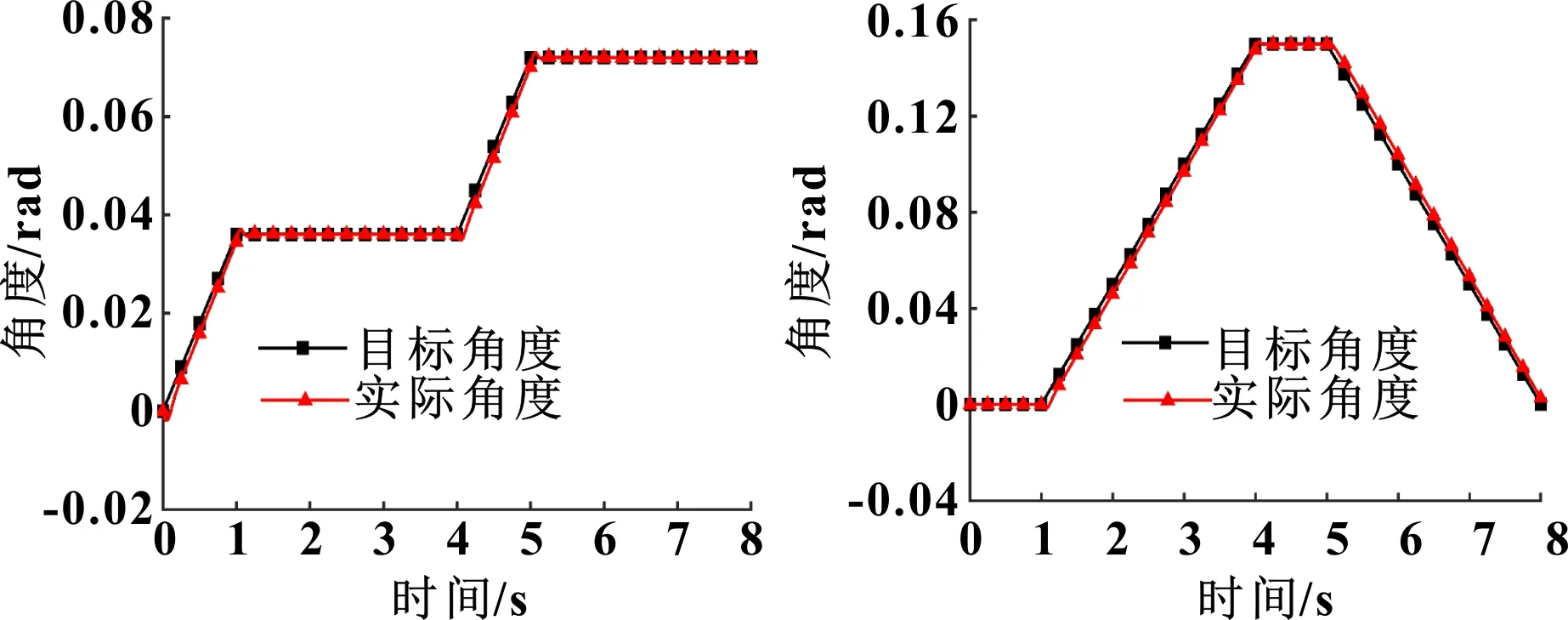
图8 悬臂升降角度曲线 图9 悬臂回转角度曲线

图10、图11分别是悬臂升降和回转角速度仿真曲线。由图10知:在0～1 s和4～5 s上升阶段，悬臂上升角速度为0.036 1 rad/s。由图11知:在1～4 s左摆和5～8 s右摆阶段，回转角速度大小为0.050 1 rad/s。但在各阶段变化处，角速度有一定的瞬时尖峰，有一定的超调。

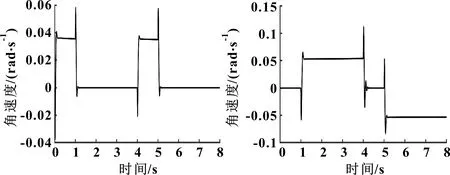
图10 悬臂升降角速度 图11 悬臂回转角速度

图12是升降液压缸压力仿真曲线。0～1 s内悬臂上升，无杆腔为进油腔，压力稳定后由13.52 MPa下降为13.34 MPa，这主要是随着悬臂的上升角度增大，活塞杆推力力臂增大所致(参见图6)；有杆腔为回油腔，回油压力为0.34 MPa。1～4 s内回转液压缸左摆，升降液压缸不动，无杆腔压力大于有杆腔压力，两腔压力差为1.718 MPa，此压力差产生的活塞杆推力与悬臂重力相平衡。4～5 s和5～8 s阶段与0～1 s和1～4 s情况类似。

图12 升降液压缸压力 图13 右回转液压缸压力

图13为右回转液压缸压力仿真曲线。0～1 s内液压缸两腔无压力；1～4 s内无杆腔为进油腔，稳态压力为12.2 MPa；4～5 s内有杆腔与无杆腔处于保压状态，两腔稳态压力为6.62 MPa；5～8 s内有杆腔为进油腔，稳态压力为12.16 MPa。

5 总结

通过对悬臂式掘进机截割部回转电液比例阀控双缸液压系统和升降电液比例阀控双缸同步液压系统的分析，结合回转和升降机械系统的结构特点，建立了悬臂式掘进机截割部系统的非线性数学模型。在MATLAB/Simulink环境构建了截割部系统闭环控制仿真模型，并对掘进机截割部典型工况进行了仿真。仿真结果表明：悬臂的升降与回转角度能够很好地跟踪目标角度，且模型能反映截割部系统各参数的相应变化情况，为后续掘进机截割头的精确定位及掘进机的自动截割提供了理论基础。