基于ROS与融合算法的AGV路径规划研究

冯浩然,吴瑞明,傅阳,陈凯旋,程强,李阳

(浙江科技学院机械与能源工程学院，浙江杭州 310023)

0 前言

随着人工智能的应用和发展，传统生产运输方式将逐步被淘汰，自动引导车(Automated Guided Vehicle，AGV)的应用与开发得到了越来越多的关注，并应用于各个领域。AGV在智能制造业中占有极其重要的地位，是现代智能仓储和物流系统的关键组成部分。AGV具有自动化程度高、柔性化程度高以及可靠性强等优点，作为一种用于物流运输的移动机器人，它已广泛应用于物流仓储及烟草等行业，而其路径规划问题也已成为当下研究的热点。

AGV已广泛应用于各种工程、运输和物流等领域，而路径规划在AGV的运动控制中极为关键，且路径规划算法的效率直接影响移动机器人的寻路效率。路径规划可以分为全局和局部规划，取决于环境和目标的性质。针对静态环境，目前已经有许多算法能够解决全局路径规划问题，如动态窗口算法、A算法、D算法、蚁群算法、遗传算法等。遗传算法在寻找全局最优解的过程中，是一个随机搜索的过程，当节点增多时，搜索时间会变得较长。而A算法是一种启发式搜索算法，也是目前应用最广泛的算法之一，实现容易，搜索效率高，具有一定方向性。传统的A算法也存在转折点过多、节点冗余、避障安全性考虑不充分等问题。传统A算法倾向于关注最短路径，通常产生一条接近障碍物的路径。 而在实际应用中，AGV可能会偏离计划轨迹，这是由传感器测量误差和车轮的滑移引起的。选用动态窗口法进行路径规划虽然可以使AGV具有优良的避障安全性，路径平滑，但很容易陷入局部最优，无法以最短距离到达目标点。针对上述问题，对传统A算法和动态窗口法进行改进并融合。利用A算法进行全局路径搜索后，去除多余节点和改进安全避障距离；结合改进动态窗口法完成局部路径规划，为AGV规划出一条避障安全性好、平滑度高、具有实时性的最优路径。

1 改进A*算法

1.1 传统A*算法

A算法因简单高效而被广泛应用。它是一种典型的启发式搜索算法，也是一种图形搜索算法，通过评价函数来确定搜索方向，并将启发式信息用于评价函数。这不仅利于找到最优路径，而且可减少搜索时间。该算法从起始节点开始构建路径，不断将当前节点的周围栅格中心点加入OpenList，且不断选取OpenList列表中值最小的点作为当前节点，直到当前节点的周围节点出现目标节点或者OpenList为空时停止。该算法公式为

(,)=(,)+(,)

(1)

距离函数(,)一般取欧氏距离或曼哈顿距离，为提高算法准确率，文中采用欧氏距离：

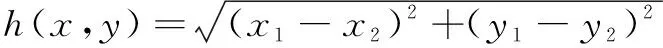
(2)

其中：、分别为起点的坐标与坐标；、分别为目标点的坐标与坐标。

1.2 设置OpenList访问时间阈值

在传统A算法中，当当前节点扩展子节点时，每次都会扩展所有候选节点。这种方式在复杂的环境中可能会存在无效搜索，影响算法运行效率。因此，在传统A算法基础上加以改进，避免陷入局部最优解，以真正规划全局路径，并提高搜索能力。具体改进方法：每次检测OpenList中的第一个插入节点，判断它是否在经过一定时间阈值后被扩展，如果没有，则该节点将被视为最高优先级扩展。

1.3 Floyd算法优化

Floyd算法指采用动态规划的思想来搜索最短路径，用于求解两点之间的最优距离问题。采用Floyd算法和A算法相结合的改进策略，可以减小路径长度，满足应用需求。Floyd算法原理如图1所示。

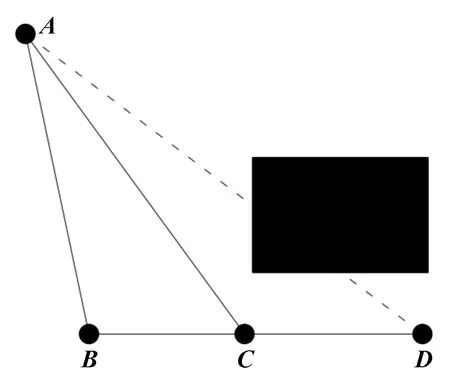
图1 Floyd算法原理示意

设(,)为点与点之间的距离，(,)为点到点的路线，而在图1中，如果与之间存在障碍，则设(,)=∞，与之间无法直接连接通行。

设点是点与点之间的计划节点，如果:

(,)+(,)=(,)

(3)

则：

(,)=(,)+(,)

(4)

(,)=→→

(5)

设点是点与点之间的计划节点，如果：

(,)+(,)<(,)+(,)

(6)

则：

(,)=(,)+(,)

(7)

(,)=→→

(8)

删除点，优化路径为从点到点再到点。采用Floyd算法优化A算法规划的路径，可以去除冗余点，进一步优化路径。

1.4 安全避障路径的改进

AGV运动过程中可能会与障碍物发生碰撞，对此进行算法优化。若相邻节点和当前节点的父节点关于当前节点的方向相同，则减小(,)值，反之则增加(,)值。在扩展子节点的过程中，优先扩展水平方向上的节点，随后判断水平方向上是否存在障碍物，如果存在，则不扩展与障碍物相邻的对角线节点；如果不存在，则扩展对角线方向节点。安全避障路径生成策略的流程如图2所示。

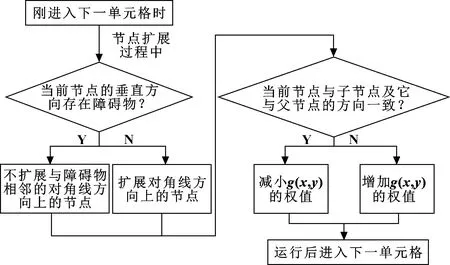
图2 避障优化流程

2 动态窗口法

在仓储物流环境中，室内大多数物体按照一定设计放置，其位置已知，但存在一些移动物体如工人，因此很难获取完整环境信息。为避免撞伤人，保证AGV的安全性，在全局路径规划的基础上，采用动态窗口法进行局部路径规划。

由于动态窗口法具有符合AGV的运动特征、灵活性强等优点，动态窗口法成为动态环境下局部避障的主要算法。在AGV运动过程中，动态窗口算法实时预测AGV的速度与状态空间，获取其多组预测时间内的可行运动轨迹，再根据设计的评价函数选取最优运动轨迹的线速度与角速度，完成路径规划，从而获得一条更安全且平滑的最优局部路径。

2.1 AGV运动模型

动态窗口算法将AGV的位置控制转换为速度控制。在利用速度模式对AGV运动轨迹进行预测时，首先需要对机器人的运动模型进行分析，通过对AGV的速度进行空间采样，模拟出其运动轨迹。AGV的线速度和角速度的变化能够反映出AGV的运动状态，(,)代表AGV在世界坐标系下的平移速度与角速度，表征其轨迹。通过评价函数在所有可行轨迹里选取最佳轨迹，在采样周期Δ内，假设AGV作匀速直线运动，则其运动模型为

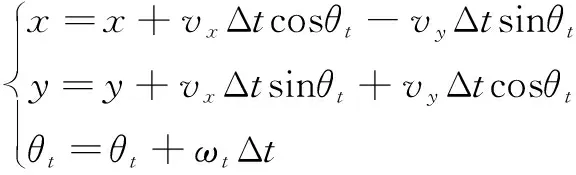
(9)

2.2 AGV速度采样

在速度搜索空间中,根据AGV及其环境所得到的一定范围内的无穷多组(,)对采样速度范围进行约束，其限制因素可分为3种：AGV本体速度约束、加速度约束以及障碍物约束。

AGV速度约束:

={(,)|∈[,],∈[,]}

(10)

AGV加减速度约束。动态窗口下的采样周期内，由于AGV加速度受电机力矩限制，AGV受到该限制所带来的最大、最小速度限制：

={(,)|∈[-Δ,+Δ],∈[-Δ,+Δ]}

(11)

其中：和分别为当前时刻的线速度和角速度；和分别为当前时刻的最大速度和最大加速度；和分别为当前时刻的最小速度和最大减速度。

AGV制动约束。考虑到AGV安全性，需要保证AGV不与障碍物发生碰撞，则在局部路径规划时的最大减速度条件下，其速度约束为

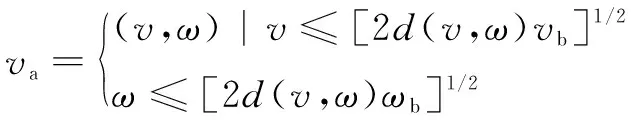
(12)

式中：(,)是(,)对应轨迹中离障碍物的最近距离。

2.3 AGV评价函数

对于速度空间内若干组可行的采样速度，设计使AGV尽可能规避障碍物及最短时间内到达指定点的评

价函数，以选取最优路径轨迹。设计的评价函数为

(,)=(,)+(,)+(,)

(13)

其中：(,)为当前速度方向与目标位置之间的偏差角的评价函数；(,)为速度轨迹中与障碍物之间的最短距离；(,)为当前轨迹速度大小的评价函数;、、分别为各项的加权系数。

3 融合算法

利用传统动态窗口算法进行规划时，如果没有预先进行全局路径规划而只有指定位置方向的指引，则在障碍物较多情况下，运动过程中容易陷入局部最优，导致规划轨迹无法达到全局最优。而A算法可以得到全局最优解，故将两者融合进行路径规划，充分发挥两算法的优点，实现路径长度、平滑度和安全性的全方面优化，提升动态规划路径的全局最优性。

3.1 环境模型描述

环境建模采用栅格法，如图3所示，利用单位栅格对地图进行划分，形成正方形栅格地图，并根据实际环境将AGV可自由移动区域定为白色栅格，障碍区域定为黑色栅格，如图3所示。

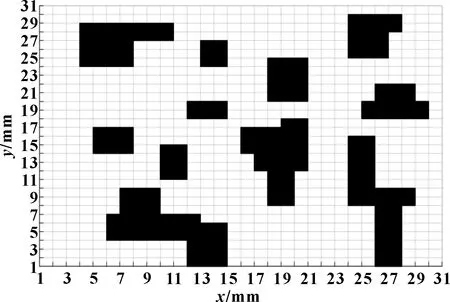
图3 环境建模栅格图

3.2 仿真实验

为验证所提出的融合算法在复杂环境中进行路径规划的有效性，进行仿真对比验证。为充分体现对比效果，设AGV的最大线速度为1 m/s，最大角速度为20.0 rad/s，最大线加速度为0.2 m/s，最大角加速度为50.0 rad/s，线速度为0.01 m/s，角速度为1 rad/s，周期为3.5 s，各算法中设定的AGV运行参数相同。实验环境为运行内存为16 GB的64位WIN10操作系统，实验平台为MATLAB2019a。

在建立的栅格模型中，假设AGV路径规划中的起点坐标为(30,30) mm、终点坐标为(8,2) mm。在静态环境中运行传统A算法，结果如图4所示。在静态环境中运行改进A算法，如图5所示，成功地完成了静态全局路径规划。为验证动态环境中的路径规划，在静态环境运行结束的基础上，设置黄色栅格的临时动态障碍物。图6所示为AGV局部动态环境下运行后的路径规划运行过程，图7所示为AGV局部动态环境下运行后的结果。表1所示为3种算法性能指标对比。利用传统A算法得到的路径总长度为44.384 3 mm,用时0.535 31 s，而改进后的A算法路径总长度为41.218 9 mm，用时0.290 545 s，相比传统A算法，改进A算法转折点和冗余路段更少，路径更短，平滑性更好且经过障碍物时可保持一定距离，安全性更好。利用动态窗口算法可实现路径的实时规划，弥补A算法时效性差的缺点，可以实现规避已规划路径上动态障碍物的功能，得到一条平滑、安全的最优路径。

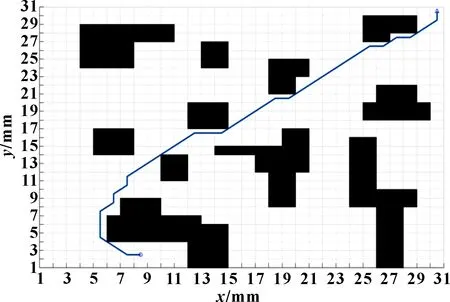
图4 传统A*算法路径规划结果

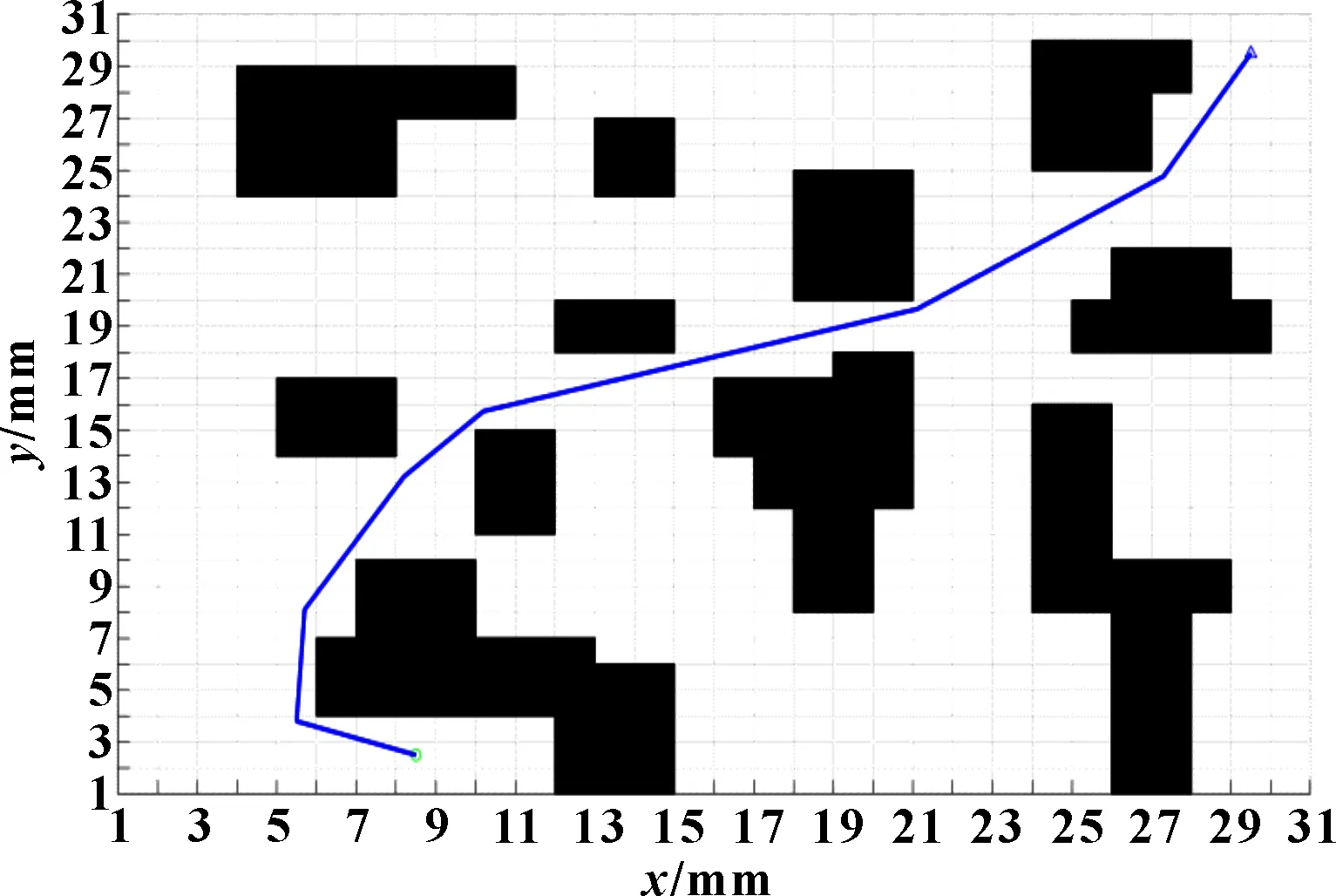
图5 静态环境路径规划结果

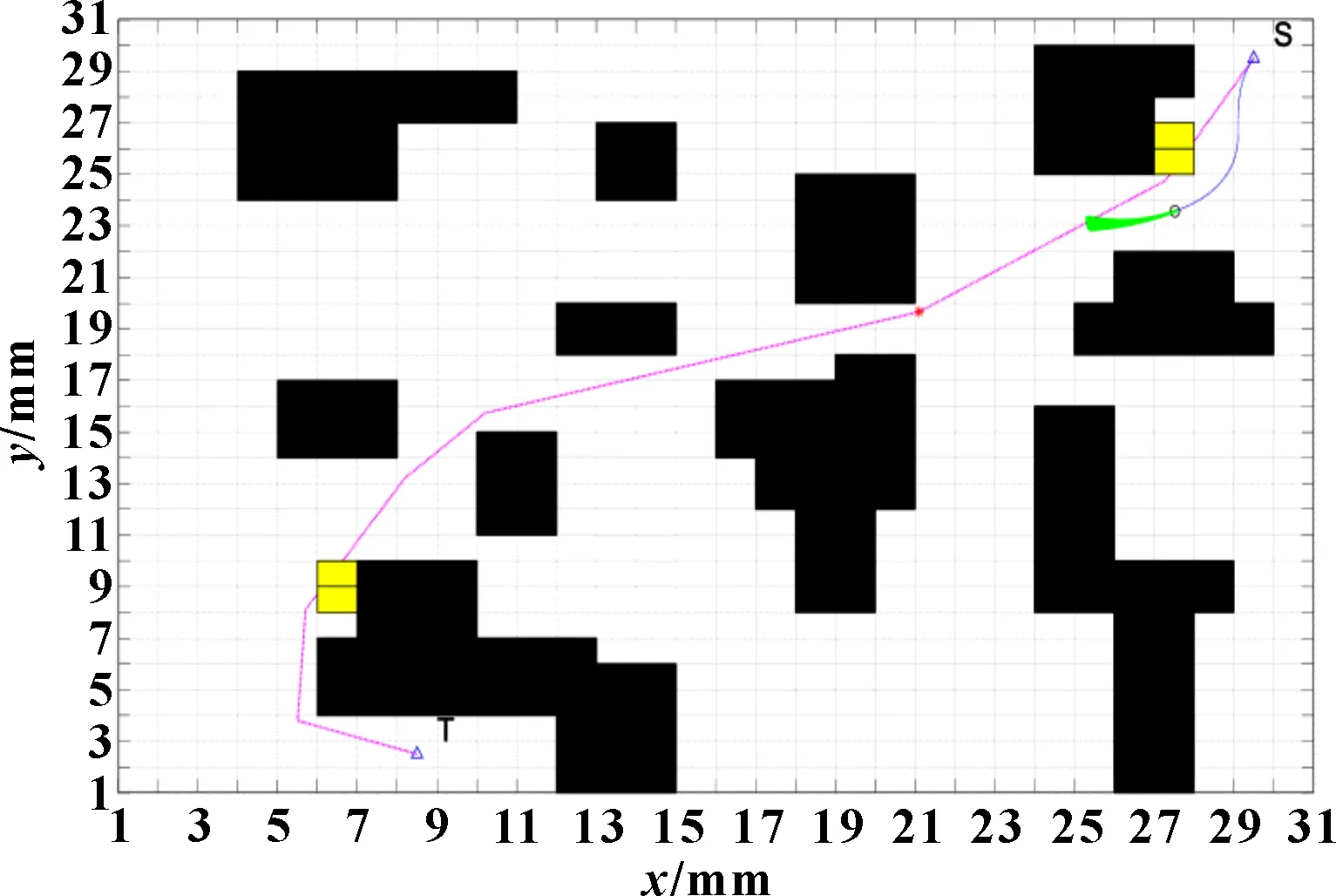
图6 动态避障路径规划过程

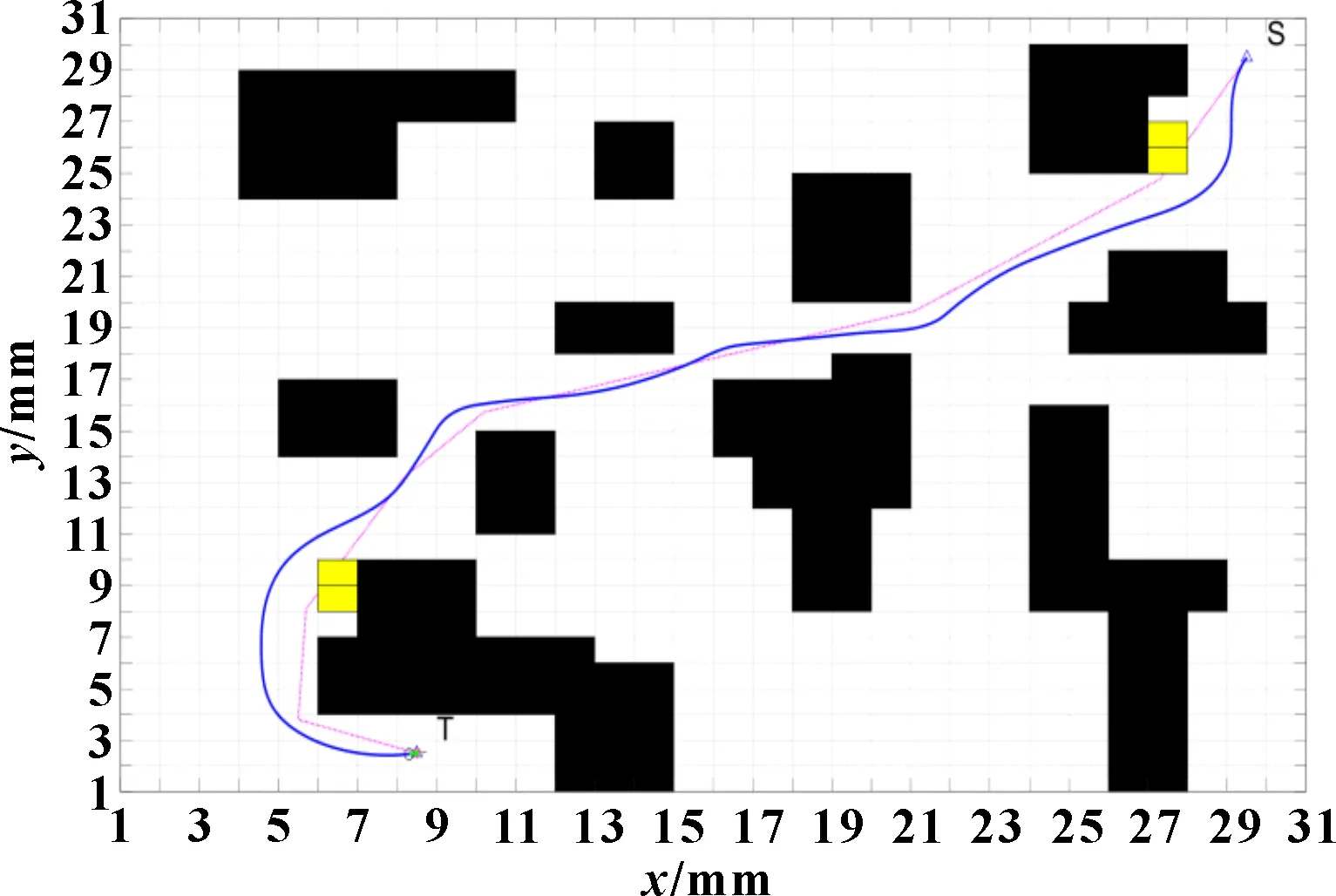
图7 动态避障路径规划结果

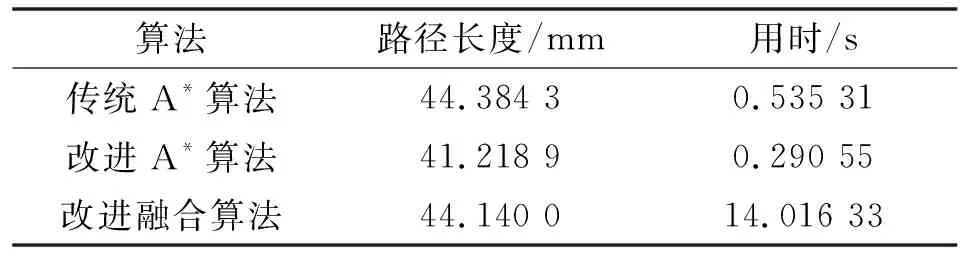
表1 各算法性能参数比较

3.3 输出运动参数

所提出的改进A算法与动态窗口法的融合算法可实时输出AGV的控制参数，有利于AGV闭环控制。AGV各参数变化如图8—图10所示，当AGV在局部路径中躲避障碍物时，可以看出线速度和角速度均减小了，且位姿发生对应的变化，验证了算法的可行性。

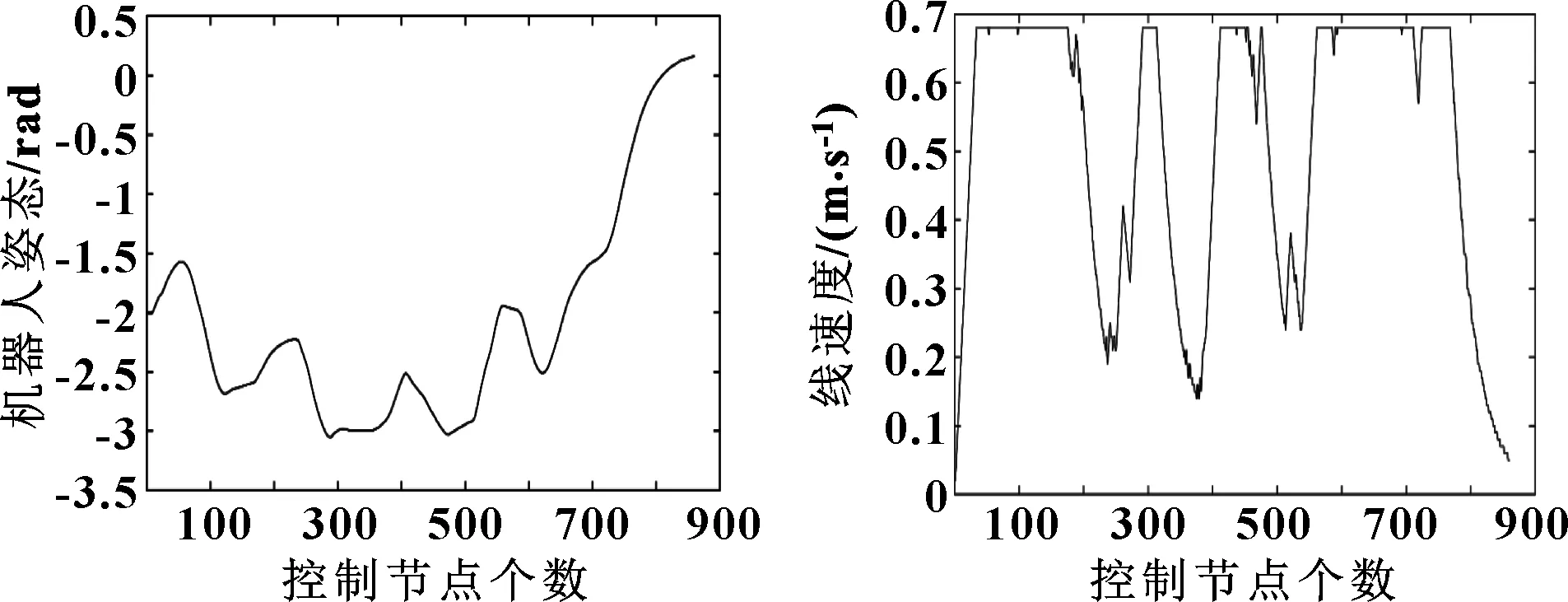
图8 AGV姿态变化曲线 图9 AGV线速度变化曲线

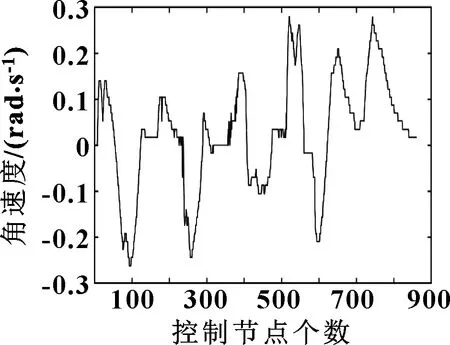
图10 AGV角速度变化曲线

4 实验验证

将改进后的融合算法应用到所研究的AGV上，AGV车体框架采用6061钢材制作，车轮采用聚氨酯制作，AGV控制系统组成如图11所示。本地PC与AGV上的树莓派4B进行数据交互，树莓派控制AGV在未知环境中通过思岚A2激光雷达实时收集周围环境信息，并实时构建地图。通过WiFi，AGV能够接收本地PC发布的控制指令，向控制单元的STM32F103单片机发送速度控制指令，实现对电机的驱动控制。驱动单元部分采用两个中间驱动轮差动驱动，驱动电机为AGV提供主要的驱动力。驱动电机决定AGV的功率性能和负载能力，从性能方面应选择中大24 V直流无刷电机作为AGV的驱动电机。

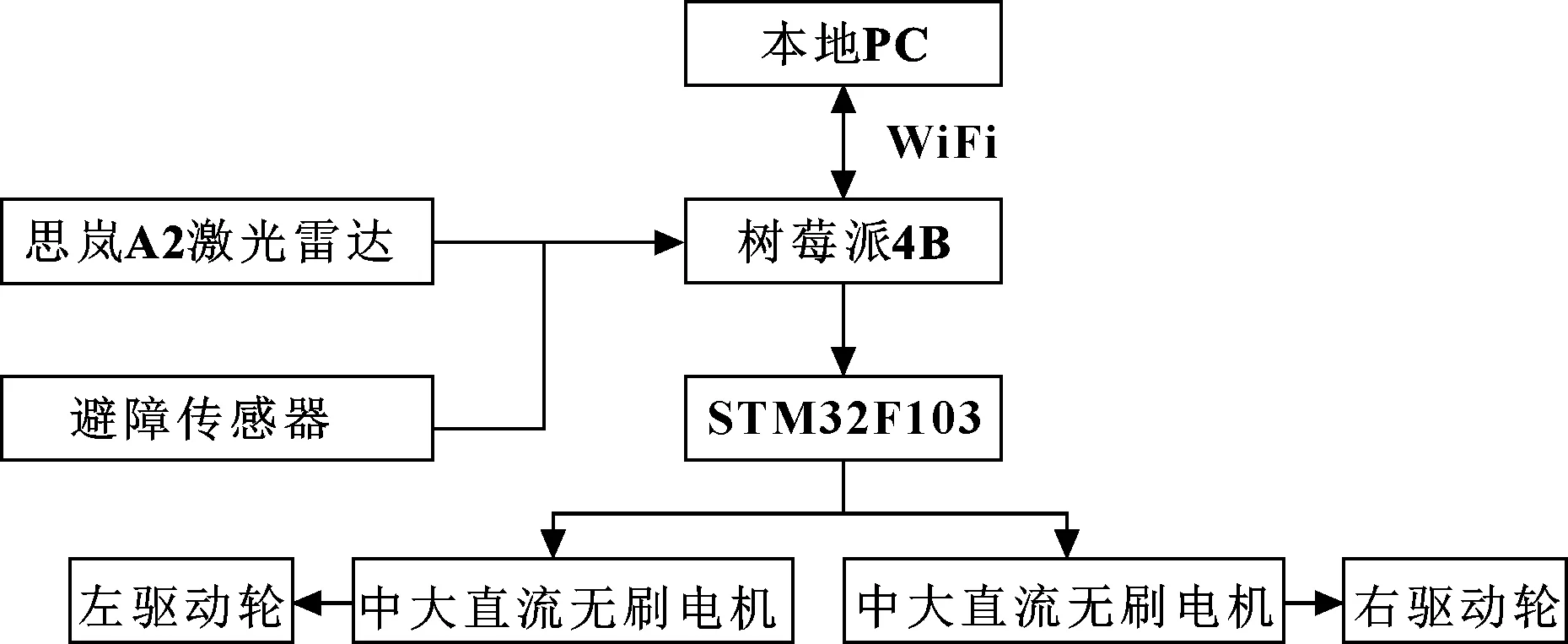
图11 AGV控制系统组成

融合算法的验证结合ROS机器人操作系统进行，通过激光雷达扫描实际环境并建图，如图12所示；再设定机器人作业起点与目标点。

图12 构建的实际环境地图

通过SLAM算法实时获取机器人当前位置信息，采用优化后的算法规划AGV当前位置至终点的最优路径，如图13所示。

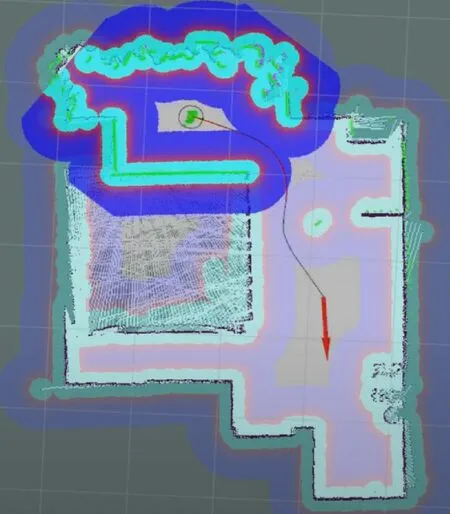
图13 AGV初始路径规划图

在AGV运动过程中，通过激光雷达实时检测动态环境变化，转为障碍物信息发送给AGV，得到环境变化后的最优路径，AGV按照最优路径进行作业。实际环境中AGV运动时会产生略微滑移现象，转角位置会有些许偏移，但是并不影响AGV的路径规划和避障，因此可忽略不计。实验过程如图14所示，首先AGV规划好最优路径，在遇到障碍物后实时更改路径，实时选择最优路径。通过实验验证，改进算法后的AGV能有效避开所有障碍物，平稳到达目标点，具有良好的避障能力和安全性，且路径平滑，满足实际作业要求。

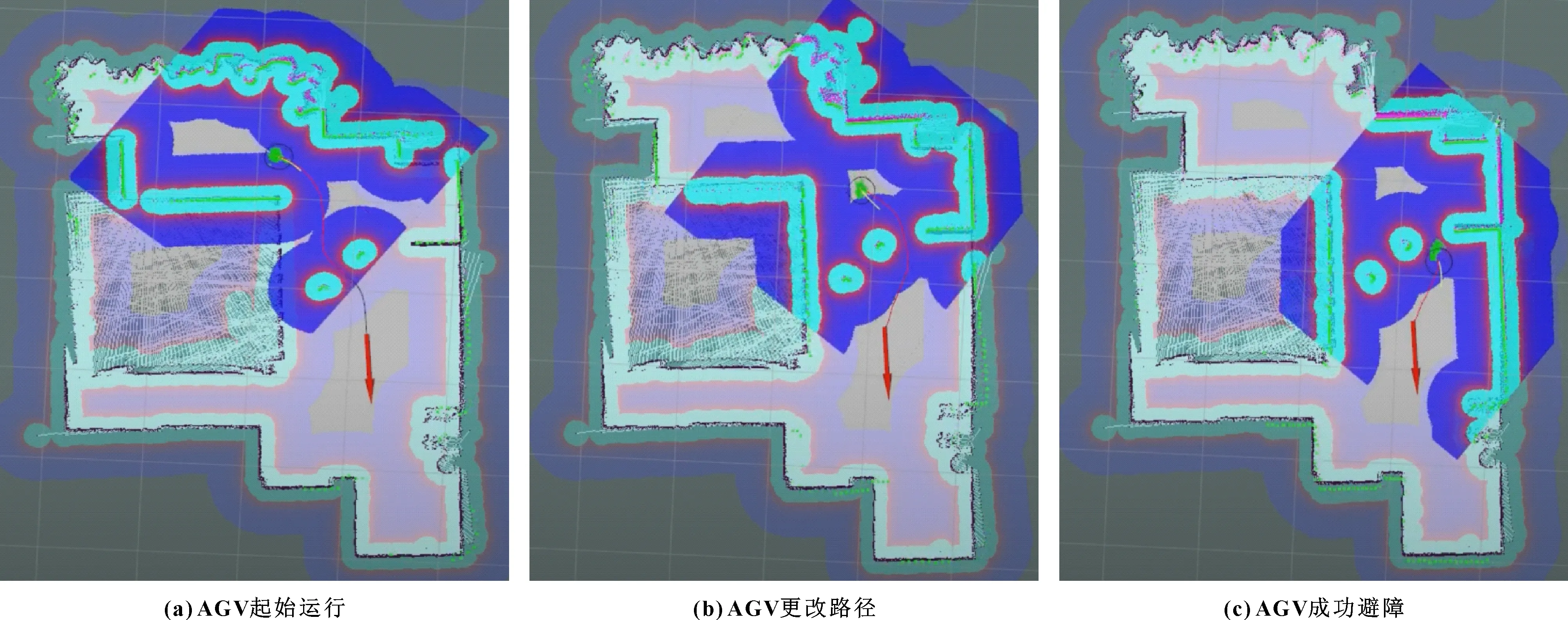
图14 AGV路径规划过程

5 结语

为提高在复杂环境下AGV的运动规划效率，并提高其安全合理的动态路径规划能力，提出了一种改进融合算法。通过改进A算法的启发函数，去除多余节点和改进安全避障距离，有效克服了传统算法转折角过多而影响AGV的正常运行作业问题，提高了AGV的安全性。同时，采用动态窗口算法实现路径的实时规划，弥补了传统A算法时效性差的缺点，实现规避已规划路径上的动态障碍物的功能，可规划出一条具有实时性的最优路径。通过仿真实验，验证了该方法切实可行，更符合实际应用。进一步地，可将它与机器视觉相结合，对复杂环境的AGV路径规划进行更深入的研究。