基于并联机构的波浪浮体运动模拟控制系统设计

乔栋，谢亚龙，杨宏娟，姚涛，张清瑞，李博文

(1.山西大同大学建筑与测绘工程学院，山西大同 037003；2.山西大同大学煤炭工程学院，山西大同 037003；3.山西大同大学机电工程学院，山西大同 037003；4.河北工业大学机械工程学院，天津 300401)

0 前言

海波发电工程领域中，波浪作用在波能转换装置上，会使其产生随波浪起伏垂荡、横摇与纵摇运动，从而吸收波浪的机械能。对波浪浮体的运动进行模拟，将有利于分析波浪发电装置的工作情况及波能转化效率。并联机构能够实现空间多自由度运动，具有刚度大、承载能力强、运动精度高等优点，基于并联机构的运动模拟装置能较好体现波浪浮体的动态稳定性及其可靠性。

近年来，针对并联机构运动模拟系统的运动学、动力学理论以及控制策略的关键性技术研究较多。波浪浮体运动仿真方面，王小东等建立了浮体平台横摇运动模型并在长峰波随机海浪下对其横摇运动进行了仿真。周云华等针对现有船舰海况模拟平台指标制定上的不足，提出等效摇摆参数的概念，按照横摇、纵摇幅值、周期不变的情况，改变等效摇摆参数。皮阳军等利用六自由度运动模拟器复现随机海浪谱，对船载设备进行环境模拟实验。李晓、彭利坤基于并联六自由度运动模拟平台引入随机波浪模型，分析不同风浪等级对船舰姿态的影响。杨军宏等基于ADAMS进行了船舶运动模拟器及其液压驱动系统的设计与动力学仿真。

在并联机构控制器的研究中，王益群、张泽强研究了并联机构伺服系统对编码器的控制，并进行了仿真分析。王艺博针对并联机器人的运动控制系统，对其核心处理器SPI运动处理器单元进行深入分析。姚莉君等以并联机构动平台为控制对象，通过输入动平台的规划轨迹，以PID作为控制器，调节PID参数使动平台按照规定轨迹运行。郑魁敬和赵永生研究并联机床运动控制技术，采用PMAC运动控制卡和PC平台，运动系统采用“PC机+运动控制卡”结构。卢若丰等设计了一种基于舵机的Stewart平台设计，采用Arduino单片机控制。

1 基于6-RSS并联机构的波浪浮体运动模型描述

1.1 波浪浮体模型的建立

不同海洋条件对浮体会造成不同程度的摇摆、颠簸、垂荡等，通常会呈现垂荡、纵荡、横荡、横摇、纵摇、艏摇6种刚体运动位姿。一般地，风力不大于4级时，海况不大于3级，浮体摇摆度不大于5°，波浪周期为2～4 s。

假定浮体在规则波中作微幅振荡，可以将浮体在波浪作用下的运动和力简化成线性问题。根据势波理论将波浪的运动简化为正弦函数，可以表示为

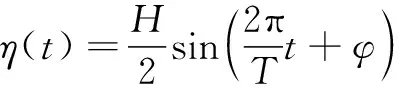
(1)

其中：为运动幅值；为运动频率；为运动相位角。研究中假定波浪浮体的运动与波浪的运动变化一致，浮体运动周期为2～4 s，摇摆角不大于5°。

1.2 位姿描述

基于6-RSS并联机构构型，设计了一种波浪浮体运动模拟器，结构简图如图1所示。机构通过6条支链与上下两平台连接。支链采用球头拉杆与上下平台形成球铰副，两端可实现自由转动。下平台由两层固定底座构成，作为机构的静平台，驱动电机置于机座上，从而减小了运动负荷。动平台相邻铰点构成的长边与静平台相邻铰点构成的短边相互平行。6个摆杆长度相同，舵机摇臂与摆杆形成曲柄连杆机构。

图1 6-RSS机构三维模型

建立动、静两个坐标系:-为静坐标系，即惯性坐标系，原点在下平台铰接点所形成的六边形几何中心;′-′′′为动坐标系，原点在上平台铰接点形成的六边形几何中心。各支链形成的矢量关系如图2所示。

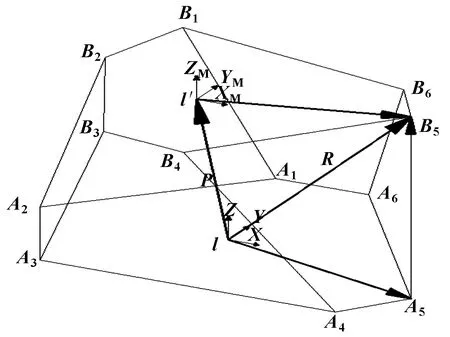
图2 矢量分析简图

下平台6个铰接点,,…,在静坐标系中的坐标向量用矩阵表示，其中第1列的第1行至第3行元素分别表示点在静坐标系中的轴、轴、轴的坐标量，其余各列与第一列意义相似。

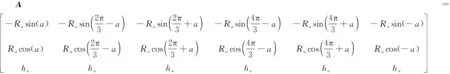
(2)

式中:是下平台的铰接点形成的分布圆的半径值;为铰接点相对于轴的偏移角度，即上平台各铰接点分布角;为下平台铰接点离下平台质心的高度。为方便下文中的计算表达式，将矩阵中三角函数后的角度值用表示。

上平台6个铰接点在动坐标系中的坐标向量用矩阵表示，其中第1列的第1行至第3行元素分别表示点在动坐标系中的′轴、′轴、轴的坐标量，其余各列与第一列意义相似。可得：

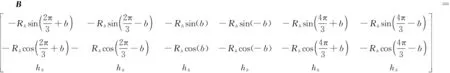
(3)

式中:是下平台的铰接点形成的分布圆的半径值；为铰接点相对于′轴的偏移角度，即上平台各铰接点分布角；为上平台铰接点离上平台质心的高度。将矩阵中三角函数后的角度值用表示。

1.3 位置反解

动坐标系中的通过坐标变换可以得到惯性坐标系中的：

=+

(4)

式中:为旋转矩阵;为上平台质心在惯性坐标系的坐标。

描述转动刚体相对参考系的姿态可以用3个角度作为广义坐标，这3个角为动坐标系与静坐标系下的姿态角(,,)，也称作欧拉角。它们用于描述刚体相对于静坐标系的姿态，由3个欧拉角构成的旋转矩阵为

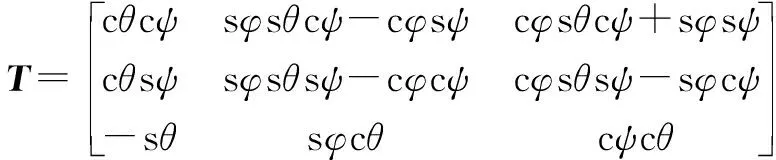
(5)

式中：c=cos，c=cos,c=cos，s=sin，s=sin,s=sin，以此类推。

为上平台质心坐标在惯性坐标系的坐标：

=(,,)

(6)

由上式求解可得，即上平台6个铰接点在惯性坐标系中的坐标，即=，进而得到向量。向量分析如图3所示。

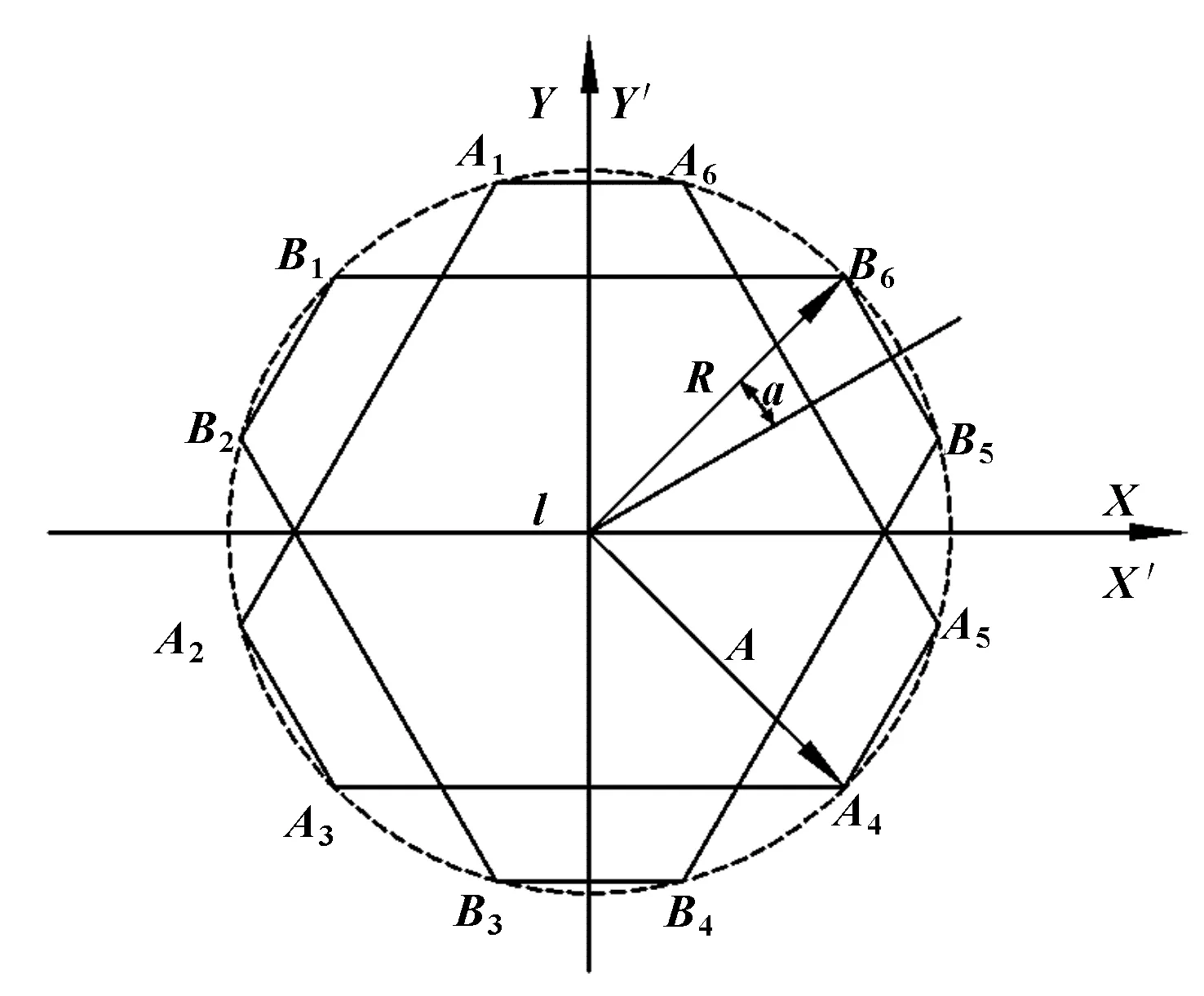
图3 向量分析简图

若动平台与静平台中间给定任意点，则坐标可由以下式子得到：

=[coscoscossincos]

=1,2,…,6

(7)

式中:是舵机的转角;是向量与正方向的夹角;是舵机摇臂长度。向量通过下式求解：

=-

(8)

联立上式，可得唯一未知变量转角。

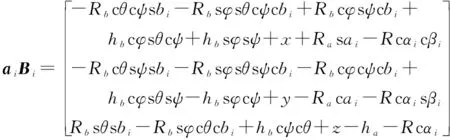
(9)

因为||=，所以：

(-ccs-sscc+csc+csc+

ss++s-cc)+(-css-

sssc-ccc+css-sc+-

c-cs)+(ss-scc+cc+

--c)=

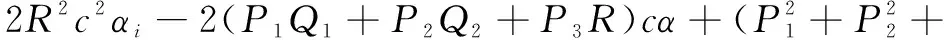
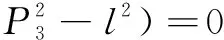
=2，=2(++)

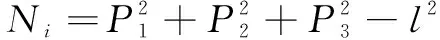
则原式为

c-c+=0

(10)

因为舵机摇臂转角在(0，π/2)之间，所以

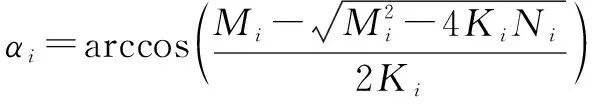
(11)

2 仿真计算

依据并联机构运动学反解的数学推导，在MATLAB/Simulink中建立位姿逆解仿真模型。如图4所示。

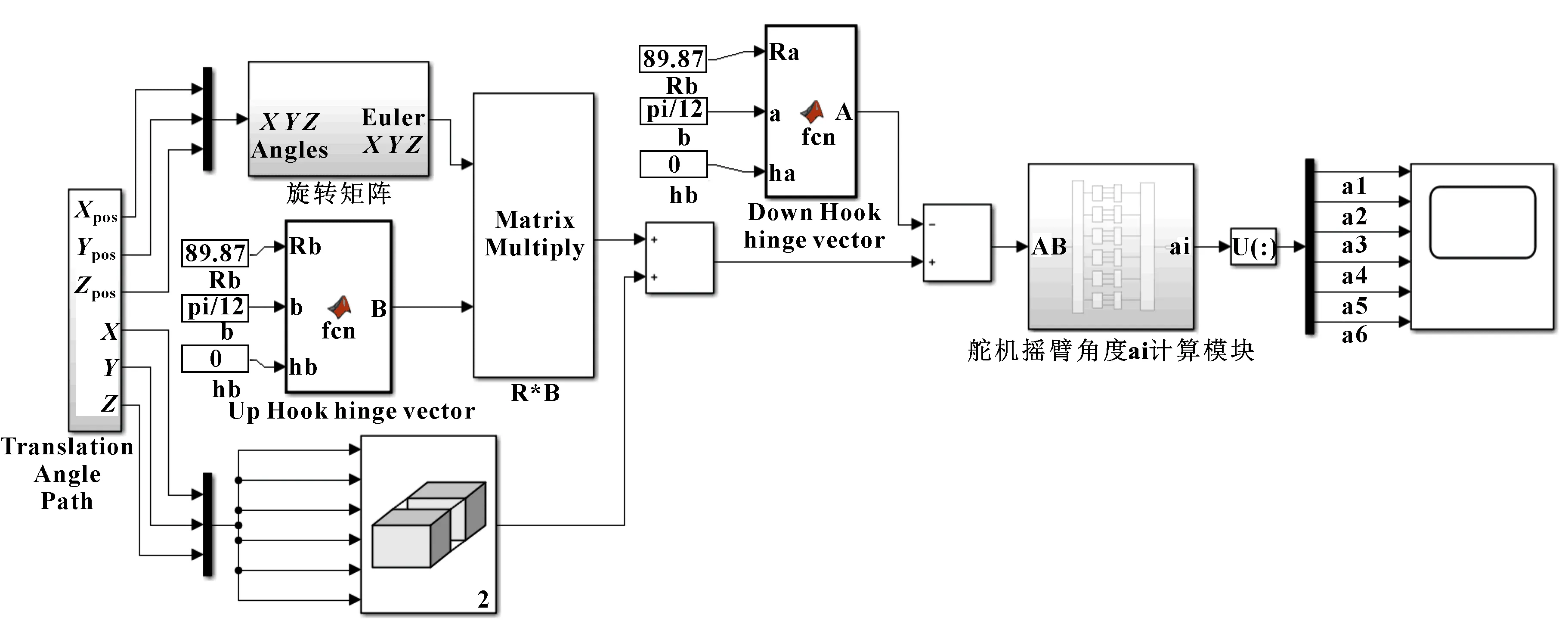
图4 位姿反解仿真模型

2.1 波浪浮体垂荡运动模拟

设置旋转变量与、平移变量均为零，平移变量输入为=129+6sin(3)，即上平台在[123，135]区间内上下垂荡。各舵机摇臂转角变化仿真结果如图5所示。可以看出：、、位置舵机摇臂转角最大值约为174°，最小值约为141°，、、位置舵机摇臂转角最大值约为39.6°，最小值约为5.7°，6个舵机转角变化趋势相同。

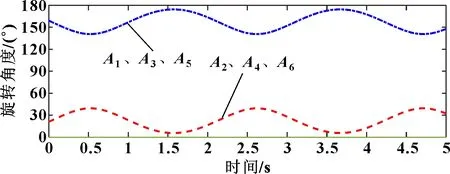
图5 波浪浮体垂荡运动舵机摇臂转角变化

2.2 波浪纵摇运动模拟

、平移变量输入为零，平移变量输入为=129，、旋转变量输入值为零，角度变量输入为=(π/40)sin(3)，即上平台在[-π/40，π/40]区间内绕轴纵摇。仿真结果如图6所示,位置舵机摇臂转角最大值约为35.6°，最小值约为8.3°；位置舵机摇臂转角最大值约为176°，最小值约为137°；位置舵机摇臂转角最大值约为26°，最小值约为16°；位置舵机摇臂转角最大值约为164°，最小值约为154°；位置舵机摇臂转角最大值约为42°，最小值约为3.8°；位置舵机摇臂转角最大值约为172°，最小值约为144°。、、、位置舵机摇臂转角变化趋势相同，、位置舵机摇臂转角变化趋势相同，且、、、与、位置舵机关于轴对称，且变化趋势相反，运动平台实现了绕轴的纵摇。

图6 波浪浮体纵摇运动舵机摇臂转角变化

2.3 波浪浮体横摇运动模拟

、平移变量输入为零，平移变量输入为=129。角度变量输入为=(π/40)sin(3)，、角度输入变量输入为零，即上平台在[-π/40，π/40]区间内绕轴做横摇运动。仿真结果如图7所示:位置舵机摇臂转角最大值约为35.6°，最小值约为8.3°；位置舵机摇臂转角最大值约为164°，最小值约为154°；位置舵机摇臂转角最大值约为42°，最小值约为3.8°；位置舵机摇臂转角最大值约为176°，最小值约为137°；位置舵机摇臂转角最大值约为26°，最小值约为16°；位置舵机摇臂转角最大值约为172°，最小值约为144°。、、位置舵机摇臂转角变化趋势相同，、、位置舵机摇臂转角变化趋势相同，且、、与、、位置舵机关于轴对称，且变化趋势相反，运动平台实现了绕轴的横摇。

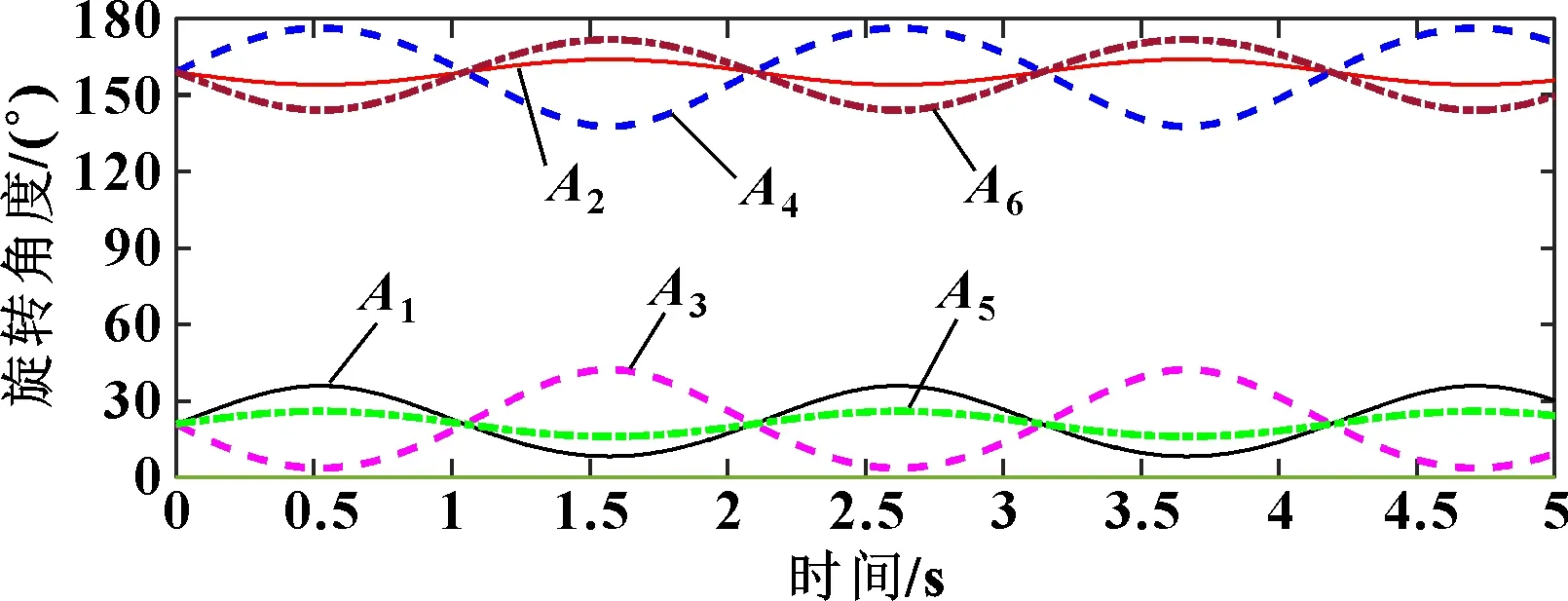
图7 模拟波浪横荡各舵机摇臂转角变化曲线

3 基于PROTUES的波浪浮体模拟控制系统设计与仿真

运动平台的控制采用Arduino控制器。在串口监视器中分别输入3个位移坐标变量、、和3个位姿角、、。系统运行代码计算对应每个舵机转动的角度，上平台即可实现相应的运动位置。整体方案包括舵机执行模块和串口通信模块。通过插补完成轮廓起点到终点之间的中间点坐标计算，并进行脉冲分配,从而控制6个舵机实现垂荡、横荡、纵荡3个自由度的运动模拟。直线插补流程如图8所示。上平台从(0，0，123)垂荡运动到(0，0，135)，直线插补函数值：chabu_line(0，0，123，0，0，135，1，10)。上平台绕轴从(0，π/40，0)纵摇运动到(0，-π/40，0)，直线插补函数值：Ola_angle(0，π/40，0，0，-π/40，0，0，0，129)。即，绕轴纵摇。上平台从(π/40，0，0)绕轴纵摇运动到(-π/40，0，0)，直线插补函数值改为：Ola_angle(π/40，0，0，-π/40，0，0，0，0，129)。基于PROTUES的控制器设计、PROTUES软件中搭建的控制系统原理分别如图9、图10所示。

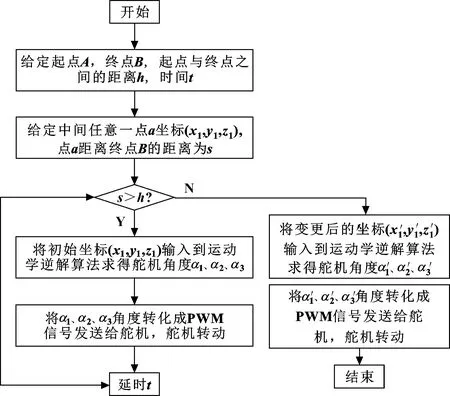
图8 直线插补流程

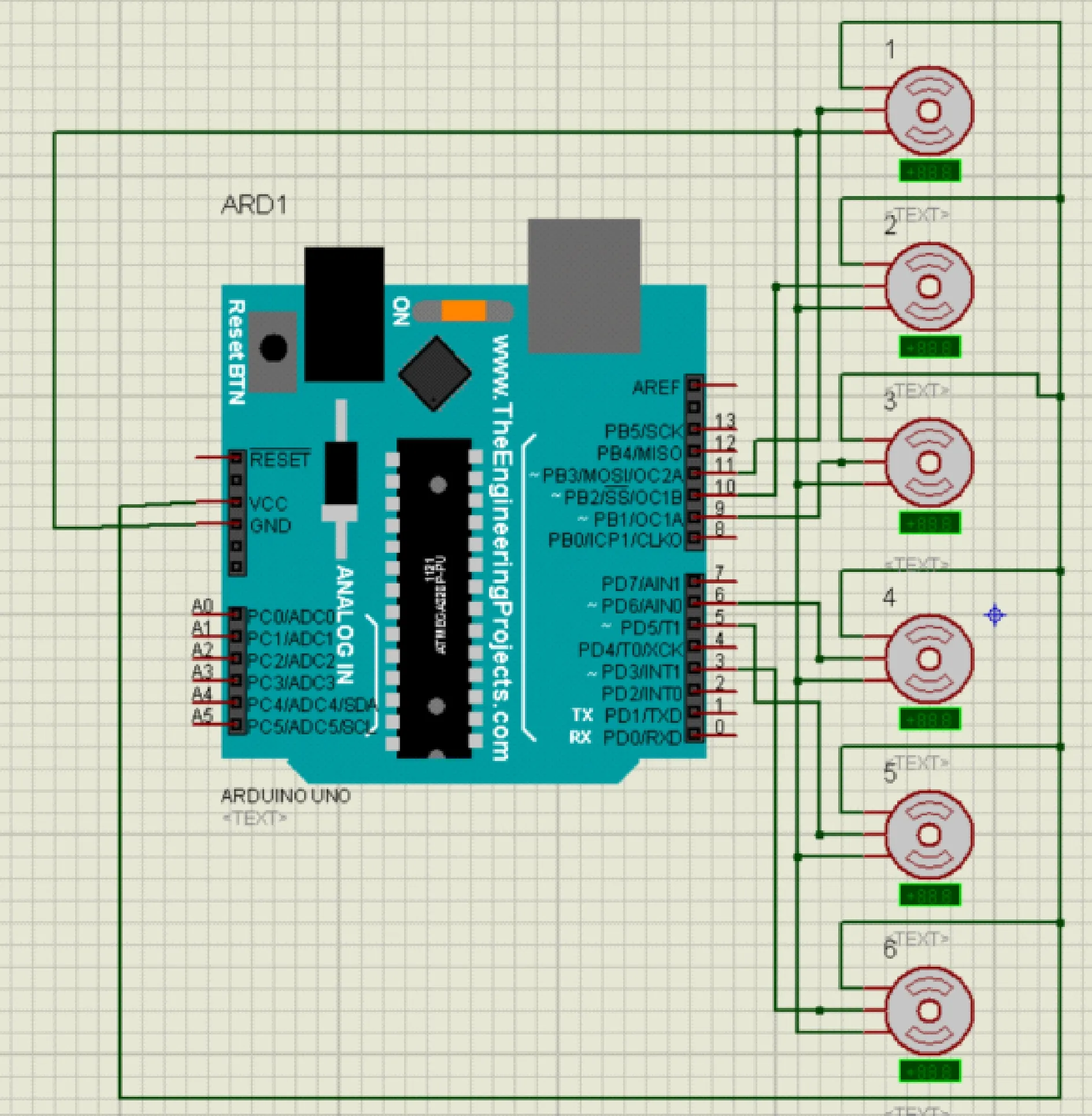
图9 基于PROTUES的控制器设计

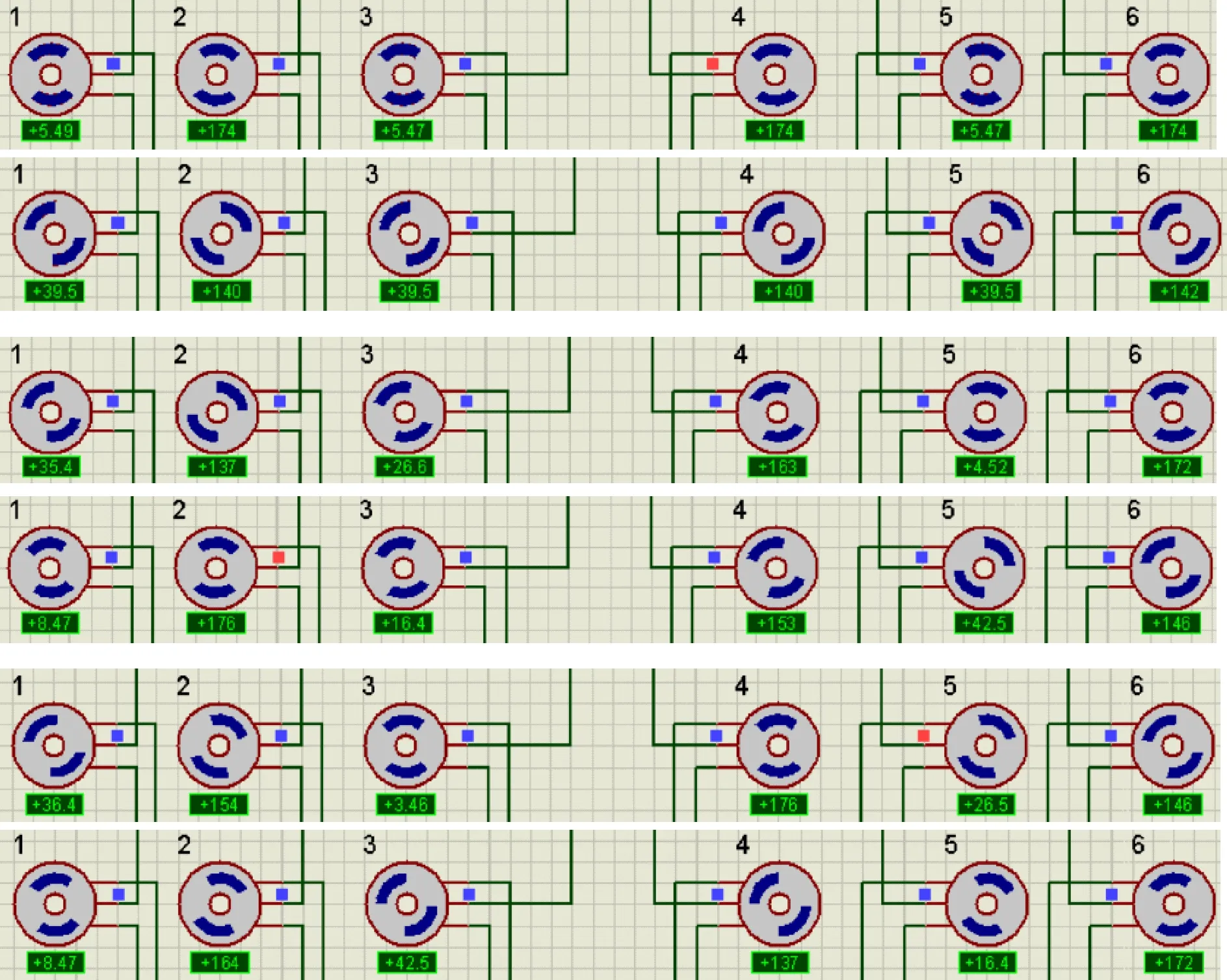
图10 PROTUES软件中搭建的控制系统原理

4 实验验证与误差分析

控制Stewart运动平台横摇的程序导入Arduino Mega单片机，控制MPU6050加速度计和陀螺仪的程序导入Arduino UNO单片机，机构控制系统垂荡、横摇与纵摇运动位姿变化实验测试如图11所示。

图11 垂荡-横摇-纵摇实验测试

实验测试中，使运动平台实现绕轴在[-π/40，π/40]角度之间的横摇。图12中MPU6050加速度计显示了平台绕轴的横摇角，角度变化从0°到4°，再从4°到0°；从0°到-4°，再从-4°到0°，满足实验预期结果。运动平台实现绕Y轴发生纵摇，期望角度变化范围为[-π/40，π/40]，运动平台实验结果如图13所示，纵摇角呈现从0°到-4°，再从-4°到0°；从0°到4.5°，再从4.5°到0°的变化趋势，与期望姿态变化保持一致。

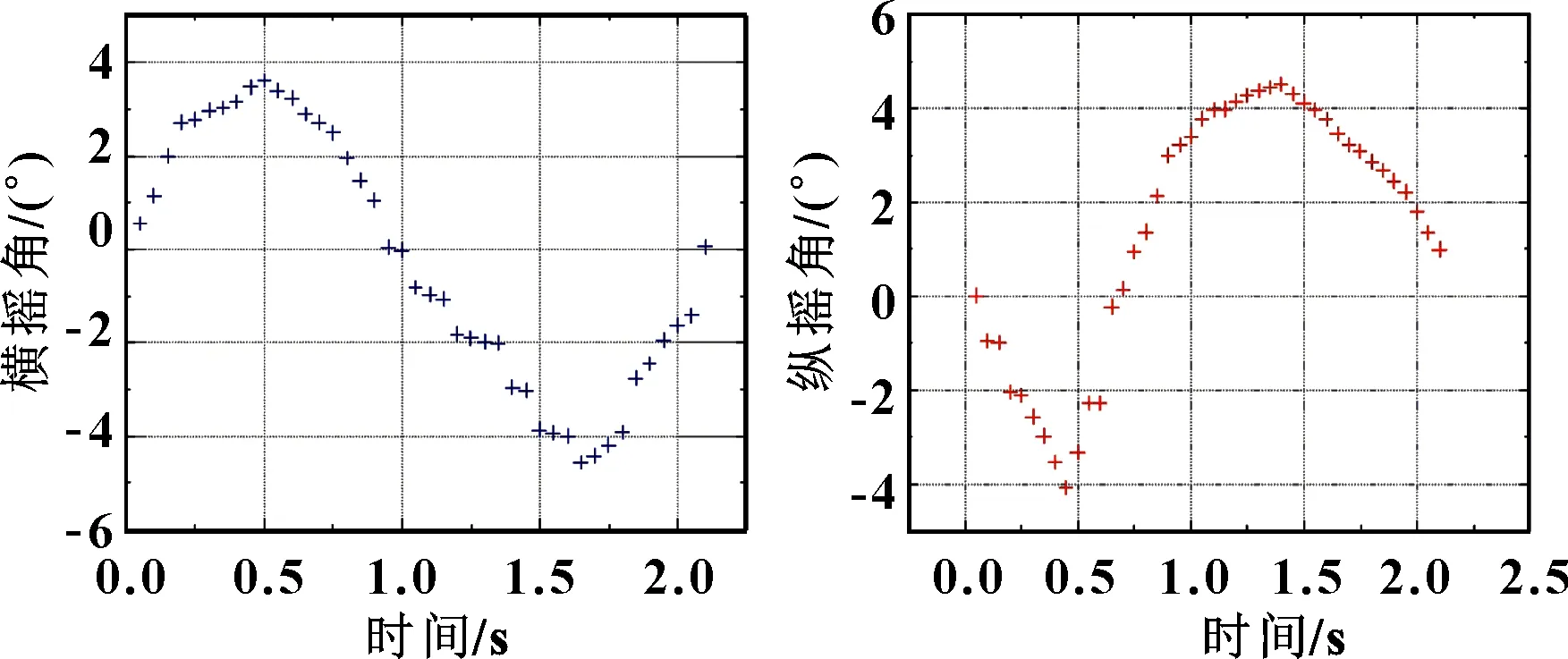
图12 横摇角实测值 图13 纵摇角实测值

基于6-RSS并联机构的控制系统实验平台可以模拟波浪的垂荡、纵摇和横摇3个自由度的运动，但是从数据可以看到，运动平台纵摇运动角度范围为(-4°，4.5°)，运动平台横摇运动角度范围为(-4°，4°)，与实验输入的角度值(-π/40，π/40)即(-4.5°，4.5°)存在误差。分析误差的原因：(1)来自于Stewart模型的机械连接的误差，比如球面副、转动副连接部分，还有上下平台连接杆的长度存在误差，导致运动平台的角度值不准确；(2)舵机的运动精度问题，并联机构是6个舵机，不同舵机之间存在的误差导致运动精度无法保证；(3)程序可以进一步优化，使得舵机的响应更加迅速。

5 结论

结合多自由度运动模拟器的工程应用背景，设计了一种基于6-RSS并联机构的波浪浮体运动模拟装置，并在给定波浪激励下进行了浮体的垂荡、纵摇、横摇运动建模与仿真；通过推导6-RSS型并联机构的运动学反解模型，获得了对应给定波浪浮体姿态下的舵机输入驱动角，同时通过直线插补完成了浮体运动的轨迹控制；然后建立了基于PROTUES单片机的电路仿真模型，完成了波浪浮体平台的运动仿真；最后通过采用Arduino Mega单片机，MPU6050加速度计和陀螺仪搭建了运动实验平台，实验结果表明浮体在波浪作用下的运动姿态能很好地完成复现，验证了所建立模型的正确性。