机床电主轴动静压轴承性能的仿真和试验研究
2022-09-20魏士杰杨帅胡文文王建磊贾谦刘哲
魏士杰,杨帅,胡文文,王建磊,贾谦,刘哲
(1.中国航发西安动力控制科技有限公司设计研究所,陕西西安 710077;2.西安理工大学机械与精密仪器工程学院,陕西西安 710048;3.西安交通大学城市学院机械工程系,陕西西安 710018)
0 前言
装备制造业是发展国民经济的基石,一个国家强大的装备制造能力是其综合实力的集中体现。以车代磨等先进加工方式的实现需要提高数控加工中心电主轴系统的设计及制造水平,提高电主轴高速下的刚度与回转精度意义明显。液体滑动轴承具有运动平稳、承载能力高、摩擦能耗低、支承刚度高等优点,因此可以选择在高端数控机床中使用。
静压支撑的滑动轴承及液压导轨已在数控机床中获得了一定的应用,其设计的核心目标是提高数控基础在加工时的精度。SHARMA、YADAV针对静压轴承利用JFO边界条件的有限元方法获得了轴承表面油膜压力和气蚀区域。KOTILAINEN、SLOCUM设计了一种内部节流的径向静压轴承,用统计的方法计算了此轴承对制造误差的均化效应,并通过试验对计算方法进行了验证。OSMAN等通过试验研究了静压轴承的油膜厚度、油膜压力、压力分布以及流量等参数,发现油腔的尺寸和位置对静压推力轴承的性能有较大影响。针对数控铣磨床的电主轴与工作台的静压轴承和双向止推静压轴承,张从学建立了回转精度误差模型,并以该模型为基础,分析了轴和轴瓦的几种误差对轴承回转误差的影响规律;金翔、李蓓智构建了电主轴刚度计算方法,并搭建了动刚度测试平台,研究动刚度随不同转速的变化规律;熊万里等研究了气体静压轴承支撑的电主轴,从4个不同方面描述了电主轴的稳定性及刚度问题;延育东、张健利用有限元分析软件研究了数控机床电主轴及转台静压滑动轴承的设计、仿真及材料选取问题。门川皓、崔展从软件计算平台角度研究了数控机床电主轴支撑静压轴承的计算仿真问题。
上述研究者对静压轴承在机床电主轴上的应用做了深入的研究,突出了静压轴承的诸多优点,但是目前关于动静压轴承作为机床电主轴支撑形式的研究还比较欠缺,因此本文作者借鉴上述静压轴承的优点,选用动静压结合的轴承形式,针对轴承的仿真和试验技术进行了深入的分析和研究。
1 电主轴动静压轴承的结构
转子轴承系统的高刚度和高回转精度是高效高精密加工的必要保障。航空航天工业中所亟需的高速高精密车削加工中心,主要的加工材料为铝合金和钛合金。车削加工中心在加工过程中经常遇到很多外界因素的影响,导致主轴刚度达不到满意的需求。主轴刚度越高则稳定性越高,精密性和抗振性能越好。文中研究的电主轴结构简图如图1所示,该电主轴主要由转子、前轴承、后轴承、定子等几部分组成。
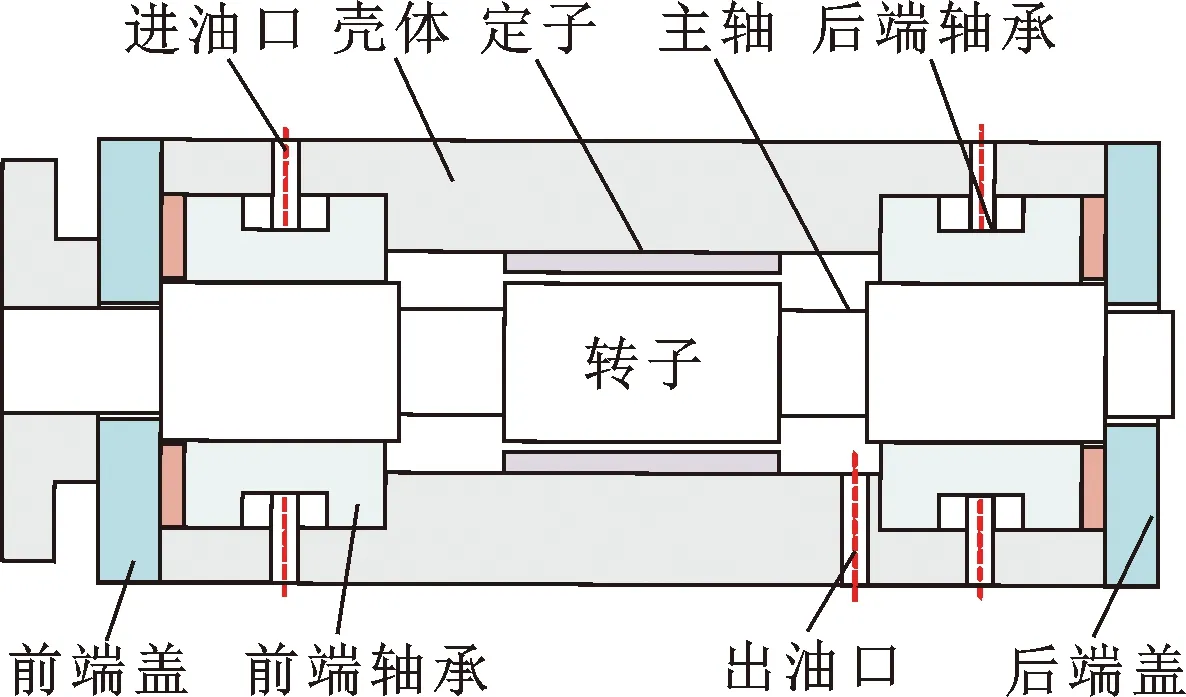
图1 车削加工中心电主轴结构示意
从表1可以看出:该电主轴的工作转速为0~8 000 r/min,由于卧式加工中心主要承受径向载荷,要求径向刚度大于2.0×10N/m;主轴在高转速工况下运转时,为维持轴系平衡,要求回转精度径向跳动不大于5 μm。为了提升加工中心精密主轴的刚度和寿命,本文作者选用了刚度大、精度高、吸振抗震性能好的动静压轴承作为精密主轴的支撑轴承。

表1 精密主轴的设计参数
所研究的动静压轴承针对的是径向前轴承,轴承选用周向四油腔带回油槽的结构,节流方式选用小孔节流。图2所示为动静压轴承的结构图。
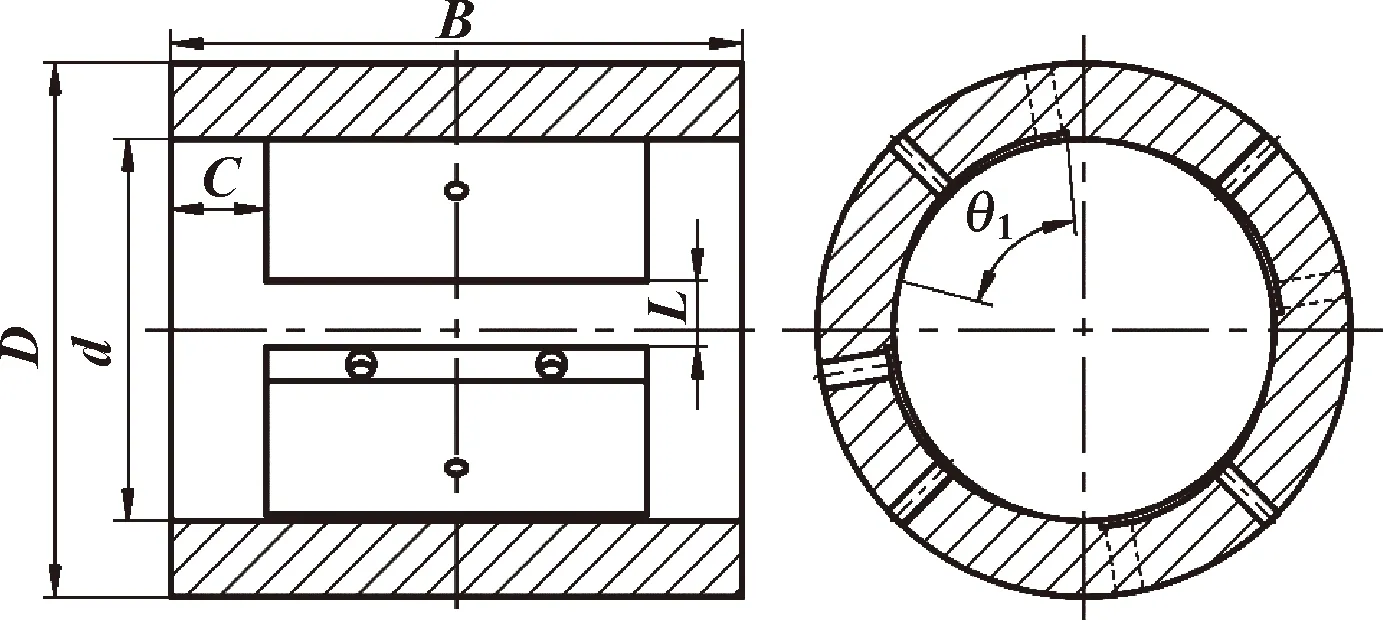
图2 动静压轴承结构
2 电主轴动静压轴承的静特性仿真
2.1 动静压轴承静特性的计算模型
动静压轴承的平衡位置如图3所示。图中:为偏心量,为油膜厚度,为偏位角。纳维-斯托克斯方程简化的用于小间隙下油膜压力求解的 Reynolds 方程的一般形式如式(1)所示:

图3 动静压轴承平衡位置示意
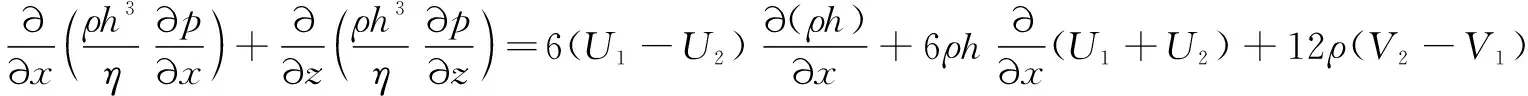
(1)
可以进行简化从而得到表示压力分布的二维雷诺方程如式(2)所示:

(2)
式中:为轴颈线速度;为润滑介质动力黏度。低黏度介质润滑轴承雷诺数比较大,因此必须考虑紊流的影响。文中采用NG和PAN理论,使用如式(3)所示的雷诺方程:

(3)
式中:和为湍流润滑系数,计算公式为

(4)
Reynolds方程的边界条件为
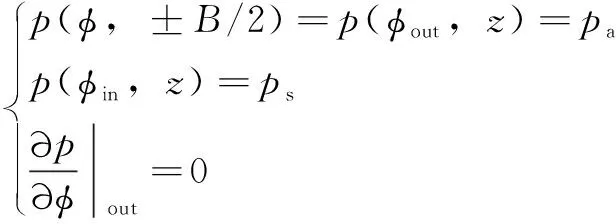
(5)
式中:为轴承出液边界;为轴承进液边界;为供液压力;为环境压力;为轴承宽度。
可采用紊流理论来同时讨论轴承的小间隙润滑问题和层流润滑,轴承和轴颈之间配合的楔形间隙形状用轴承的间隙函数来表达,油膜厚度沿周向变化,其间隙函数如式(6):
=[1+cos(+)]
(6)
式中:为偏心率;为位置角;为偏位角。
只有使节流器流入的流量和油腔流出的流量守恒,才能得到准确的求解结果。可根据轴承油膜的压力场计算出节流器流入和油腔流出的流量,如果两种流量相等则表明所设定的压力值为所需值,如果不相等则进行低松弛迭代修正,直到满足条件。轴承的油腔是对称的,因此只需取半个油腔进行研究。图4为油腔的流量示意。
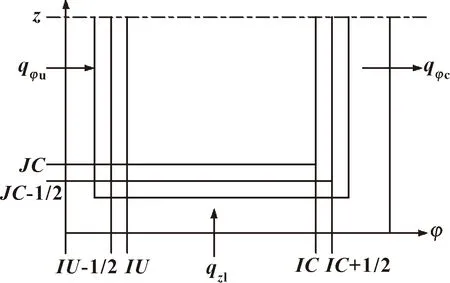
图4 油腔流量示意
沿轴向()和周向()单位宽度的体积流量分别为

(7)

(8)
若考虑湍流的影响,根据流量连续方程沿方向和单位宽度的体积流量
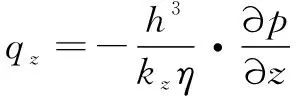
(9)

(10)
取图4所示的控制体,得流经控制体的体积流量在单位时间内的增量为
=c-u-2l
(11)
油腔的输出流量通过轴向和周向的积分求得。小孔节流器是一种常用的节流装置,它通过流体小孔形成压力降,根据节流面的位置分布还可以分为简单孔式节流器和孔式环面节流器。其中简单孔式节流器的节流面为小孔的横截面,其流量公式为

(12)
相应的小孔节流参数
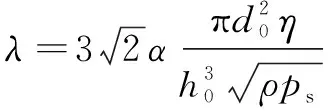
(13)
式中:为流量系数,一般取0.6~0.7;为润滑剂密度;为小孔直径。
孔式环面节流器的高度是以进油孔处的油膜厚度为准,底部的圆柱形环面为进油孔圆周面。由于轴承膜厚会随着偏心率变化,并且4个节流参数不同,其流量公式为
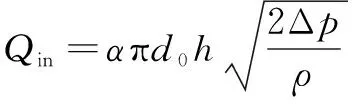
(14)
相应的节流参数:
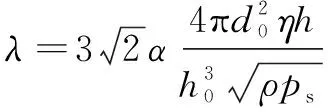
(15)
计算流程如图5所示,计算时假设流体为层流,与剪切力相比流体的惯性力非常小,可以忽略,而且在流体膜的任意位置上,膜厚方向上的密度、压力和黏度不变。另外,对于文中研究的动静压轴承,还需做不考虑转轴挠曲影响的假设。用有限差分法求解雷诺方程时,需要假设将轴承沿方向划分为120个网格,其中节点121个,节点数的编号沿着转子旋转方向递增。
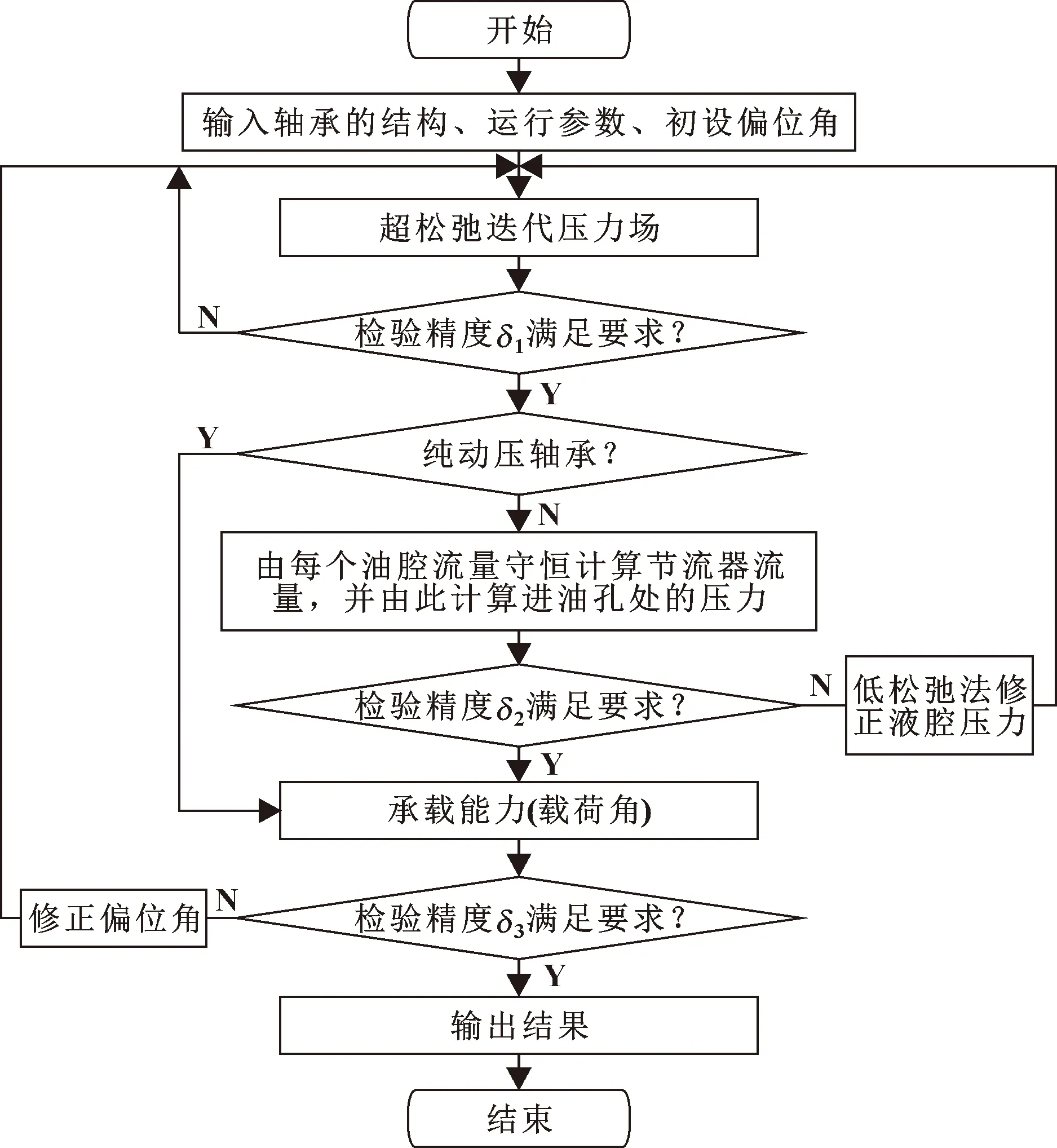
图5 轴承静特性数值计算流程
2.2 动静压轴承的静特性分析
根据电主轴的工作特点,分析的动静压轴承静特性指标包括承载力、温升和流量。而影响这些指标的结构参数主要是轴承的半径间隙和节流孔径等。所分析的动静压轴承的结构参数如表2所示。

表2 动静压轴承的结构参数
可以采用偏心率来调整动静压轴承的性能,根据不同偏心率所计算获得的动静压轴承静特性参数如图6所示。如图6(a)所示:承载力随着偏心率的增大而逐渐增大,为0.05时的值是为0.01时的7.3倍,说明增加偏心率对轴承的承载有益处。如图6(b)所示:流量随着偏心率的增加略微减小,为0.05时值比为0.01时减小了1.2%。如图6(c)所示:温升随着偏心率的增加略有增大,为0.05时的值比为0.01时增大了0.06 ℃。

图6 动静压轴承的静特性计算结果
3 电主轴动静压轴承的试验测试
动静压轴承试验装置主要由试验台主体、液压站、油液制冷机、电控箱及测试系统等组成。图7所示为试验台结构示意。试验台主体包括电机、主轴转子、试验轴承、滤油器和传感器安装支架等。在试验过程中,液压站可在供油压力为7 MPa以内稳定供油。油液制冷机的额定温度范围为22~55 ℃,电控箱的主要功能为开启关闭液压站、开启关闭驱动电机及调节电机转速。
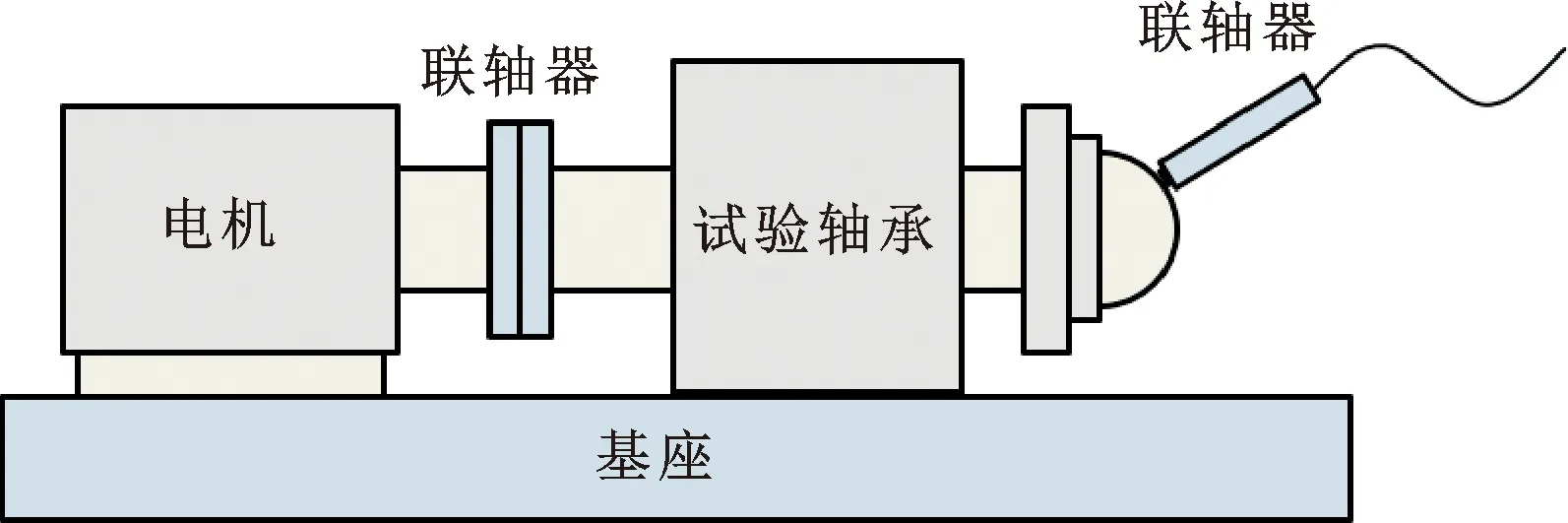
图7 卧式电主轴轴承试验台结构
借助于悬于轴端夹具上的标准球及电感测微仪可以测试转子在旋转时候的径向位移,标准球的面型精度为0.04 μm、直径为45 mm。电感测微仪的测头分别可在水平与垂直方向与标准球表面接触,反映转子振动情况,根据转子的振动数据可以获得回转精度指标。试验采用力锤激振法测试动静压轴承的刚度,用力锤沿水平或垂直方向锤击轴承座,给轴承座施加一个持续时间极短的脉冲激振,使其产生自由振动,然后分析其响应。该方法在激振力的方向上测试激振力和响应信号,可得出该轴承的刚度。
由图8(a)可以看出轴承刚度主要呈增大趋势。在1 000~8 000 r/min的转速范围内,值在2.45×10~4.16×10N/m内变化,转速在3 000~6 000 r/min时值比较稳定。图8(b)所示为转子在水平和垂直方向的振幅Δ和Δ,Δ略高于Δ,Δ和Δ的最大值分别为4.5、3.9 μm。若要提高回转精度可对转子轴系进行优化,并做好动平衡及隔振。
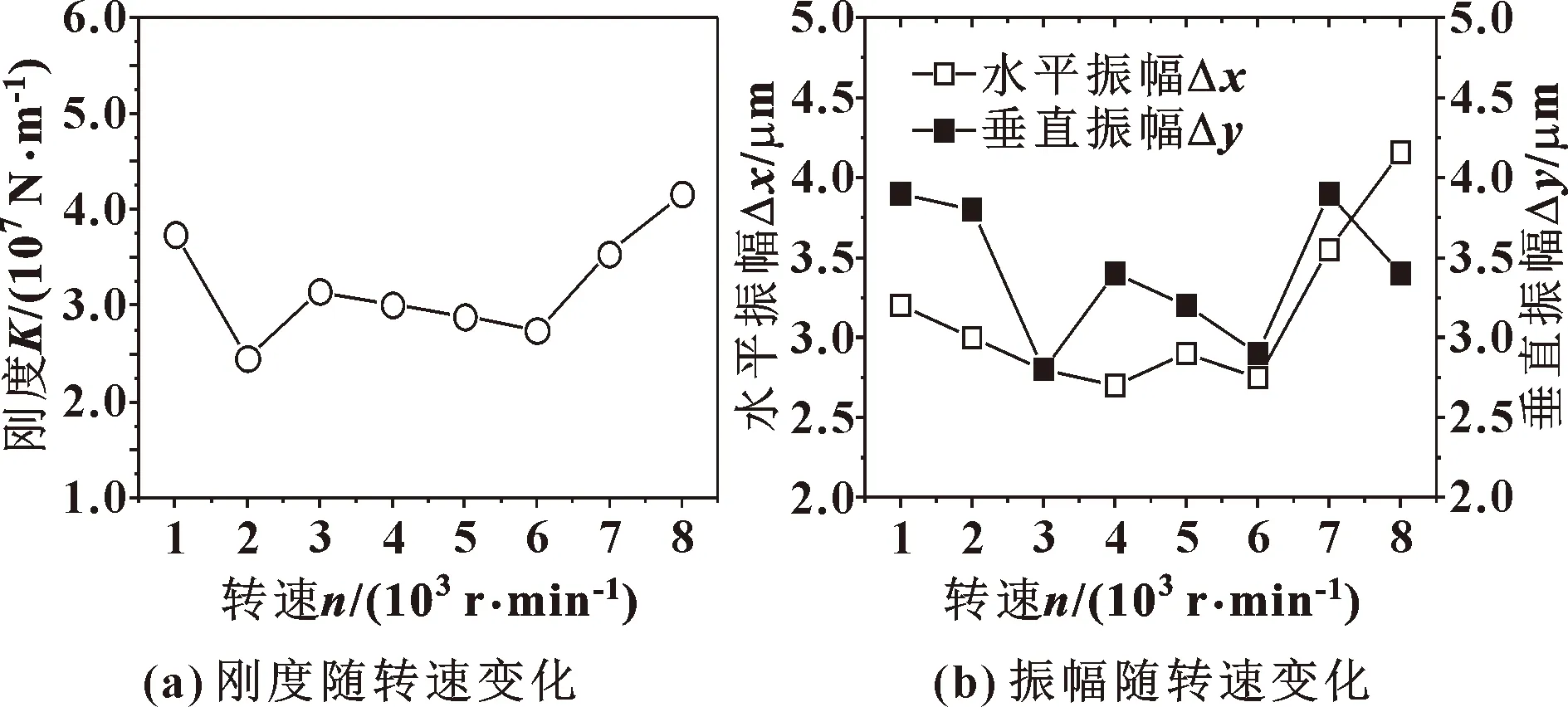
图8 刚度和振动的测试结果
4 结论
(1)针对高速精密数控车削加工中心电主轴设计了动静压轴承,轴承采用的是周向四油腔带回油槽、内置式小孔节流的结构。
(2)建立模型,通过计算仿真分析了轴承的承载力、流量和温升。随着偏心率的增大承载能力增加,流量和温升略有变化。
(3)试验测试结果说明:刚度随着转速的增加主要呈增大趋势,转速在3 000~6 000 r/min时刚度值比较稳定;水平和垂直方向的最大振幅分别为4.5、3.9 μm。
