基于改进差分进化算法的微电网调度研究

陈丹凤, 赵才, 张志飞, 周燕

(佛山科学技术学院 机电工程与自动化学院, 广东 佛山 528000)

0 引言

全球能源枯竭和环境污染的日益加重,如何提高能源利用率和减少污染排放一直是关键问题,为解决当前的微电网问题提供了新思路。微电网是一种新型的分布式能源组织结构,被视为整合可再生能源的有效平台,使可再生能源系统接入配电网更加便捷,提高能源利用率,减少污染物排放,实现分布式发电供负荷一体化运行[1-2]。目前国内外学者对微电网进行了大量的研究,也取得了较大的突破。季颖等[3]提出采用一种深度学习的方法对微电网进行调度,建立以成本最小为目标函数,通过实例仿真验证所提方法的有效性。单新文等[4]采用改进粒子群算法对蓄电池的剩余电量进行优化求解,从而整体上提高能源的利用率。林永君等[5]提出一种含多微网的主配电网分布式双层优化调度方法,上层以网损最小为目标函数,下层以经济和环保为目标函数。陈汝科等[6]以经济成本最小为目标函数,建立数学模型,采用改进内部搜索算法求解。李海涛等[7]在考虑功率平衡和各微电源功率约束条件下,采用改进的粒子群对目标函数求解,最后通过实例验证改进粒子群算法的有效性。Wang等[8]为了解决电源耗能最小的问题,提出一种粒子群遗传优化方法。该算法融合粒子群算法和遗传算法的优点,收敛速度快,精度高。Pang等[9]为了克服粒子群遗传算法的过早收敛和陷入局部最优的问题,提出一种综合学习粒子群优化算法(comprehensive learning particle swarm optimization algorithm, CLPSO),为验证CLPSO的性能，在CEC2005上对CLPSO算法进行测试。实验结果表明,CLPSO算法的求解精度总体上优于比较算法。

为了提高差分进化算法的优化性能，本文利用PSO算法的进化机制，提出一种混合多重随机变异粒子差分进化算法(particle differential evolution algorithm, DE-PSO)。首先，利用粒子差分变异策略和DE/current-to-rand/1变异策略，以提高算法的全局探索能力，同时增加种群的多样性；其次，通过引入一种简单的扰动策略，有效帮助粒子跳出局部最优，以此避免早熟收敛问题；最后，将所提算法应用到微电网能量调度中，并采用DE-PSO算法对目标函数求解，进一步验证DE-PSO算法的有效性。

1 差分进化算法

差分进化算法(differential evolution algorithm, DE)[10]是1997年由Rainer Storn和Kenneth Price提出的。该算法相对于遗传算法而言，参数少，计算相对简便，被广泛应用于电力优化调度问题，其主要过程包括初始化、变异、交叉、选择和终止5个步骤。

① 初始化。DE算法基于实数编码,在D维搜索空间中随机生成大小为NP的种群,最大迭代次数为Gmax,则第G代种群内的第i个个体可以用一个实向量Xi,G表示为

Xi,G=[xi1,G,xi2,G,…,xiD,G]T,i=1,2,…,NP,

(1)

式中xid,G(d=1,2,…,D)为Xi,G的第d个分量,满足约束条件xi,d∈[xd,low,xd,up],xd,low、xd,up分别表示搜索范围的下限和上限。

② 变异。DE算法通过种群内两两互不相同的个体向量作差分,产生相应的差分向量。在DE算法中最常用的变异策略分别为DE/rand/1、DE/current-to-rand/1和DE/best/1。具体如下所示:

DE/rand/1：

Vi,G+1=Xr0,G+Fi(Xr1,G-Xr2,G)。

(2)

DE/current-to-rand/1：

Vi,G+1=Xi,G+Fi(Xbest,G-Xi,G)+Fi(Xr1,G-Xr2,G)。

(3)

DE/best/1：

Vi,G+1=Xbest,G+Fi(Xr1,G-Xr2,G),

(4)

式中：r0,r1,r2∈[1,NP]为两两互不相同的随机数；Xr1,G—Xr2,G为随机选取2个向量的差分；Xbest,G为第G代种群中最优个体；Fi为缩放因子。

③ 交叉。第G代个体与变异的个体进行交叉形成新的试验个体Ui,G=[ur1,G,ur2,G,…,urD,G]。交叉方式一般选用较简单的二项式交叉:

(5)

式中:Pc表示交叉概率,取值为0～1；jrand为1,2,…,D上的随机整数。

④ 选择。比较试验个体Ui,G和父代个体Xi,G的优略,通过求解适应度值的大小评定优略,选择最适应度值小的进入下一代。

(6)

式中Xi+1,G为比较后成功进入下一代的父代个体。

⑤ 终止。当G达到Gmax时满足要求。

2 粒子群算法

粒子群(particle swarm optimization，PSO)算法[11],1995年由美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出的,粒子通过自身的信息并且结合种群内其他粒子的信息决定下一步的运动，具有收敛速度快、操作简单等优点,其主要原理如下所示:

假设有一D维空间,粒子Xi=(Xi1,Xi2,…,XiD),粒子i的个体极值被表示为Pbest，i=(pi1,pi2,…,piD),而Vi=(Vi,1,Vi,2,…,Vi,D)为粒子的速度矢量,即粒子的移动距离,之后通过与其他粒子间分享自己的信息,找到最优的个体极值定义为全局最优解PG，best。PG，best=(pG1,pG2,…,pGD),为粒子搜索到的全局最优位置,粒子根据式(7)、(8)调整下一步的运动,以此不断迭代往最优解靠近。

(7)

(8)

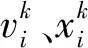
3 DE-PSO算法

3.1 粒子群差分变异策略

在PSO算法中,每个粒子通过追踪个体极值Pbest和全局极值PG,best来不断地更新速度和位置信息。此时,粒子具有一定的进化机制去记忆以往信息,然而这种进化机制在DE算法中体现的却比较少。分析表达式(7)发现，式(7)在某种程度上与DE算法中的DE/current-to-best/1变异策略类似。受此启发，利用式(7)将PSO算法的进化机制融入到DE算法中，有利于提高算法的优化性能。

(9)

式中:μmin、μmax分别为随机惯性权重的最大和最小值；σ为惯性调节因子；N(0,1)为标准正态分布。综上所述,PDE策略可表述为

(10)

3.2 DE/current-to-rand/1变异策略

PDE变异策略依赖于粒子的个体和全体的最优解,在解决单峰优化问题时具有不错的寻优性能，但是,在解决多峰优化问题时,一旦最优解陷入局部最优,那么整个算法将会提前收敛。为了补偿PDE策略的不足并增加种群多样性,引入DE/current-to-rand/1变异策略作为辅助变异算子,其数学描述如下:

Vi,G+1=Xi,G+Fi(Xbest,G-Xi,G)+Fi(Xr1,G-Xr2,G)。

(11)

3.3 随机扰动策略

根据DE算法的进化机制可以发现,最终整个种群将朝着当前的最优解进化,随着算法迭代次数的不断增加,种群间的多样性也随之逐渐减少。正如前面所提到过的,当前最优解可能是全局最优解也可能是局部最优解。如果当前最优解是全局最优解,那么它将在选择操作过程中被保存并且进入下一代种群；相反,如果是局部最优解,那么它将有可能引导整个算法陷入停滞状态。算法的种群多样性和收敛状态之间存在着密切的联系。为了增加DE算法的种群多样性以避免早熟收敛,提出一种随机扰动策略,数学描述如下:

Vi,G+1=Xmin+rand(Xmax-Xmin),

(12)

式中：Xmin、Xmax分别为解的最小值和最大值；rand是[0,1]区间内的一个随机数。此外,上述随机扰动策略也可以被用于算法种群的初始化以产生带有多样性的解,本文将其作为一种随机扰动机制以维持种群多样性。

3.4 DE-PSO算法描述

DE-PSO算法具有多重变异策略，分别为PDE、DE/current-to-rand/1和随机扰动策略。考虑到随机扰动是小概率事件，本文设定一个概率系数，当触发概率系数，即诱发随机扰动，而另外2种变异策略在算法迭代过程中随机发生。结合以上叙述，DE-PSO算法步骤如下：

Step1:初始化算法参数；

Step2:随机产生初始种群；

Step3:计算每个粒子的适应度值,并根据适应度值更新个体极值Pbest和全局极值PG，best；

Step4:执行多重随机变异操作。判断是否触发概率系数条件,如果触发,根据式(12)执行随机扰动策略；如果没有触发,则按式(10)或式(11)随机执行变异操作；

Step5:根据式(5)执行交叉操作；

Step6:根据式(6)执行选择操作；

Step7:重新计算每个粒子的适应度值,并根据计算结果更新Pbest和PG,best；

Step8:判定算法是不是最大迭代次数Gmax,如达到条件则算法终止并输出结果,否则重新返回Step 4。

3.5 数值实验分析

为了验证DE-PSO算法的有效性,本文以文献[13]中的5个基准函数为测试对象,采用DE-PSO算法、PSOGA算法[8]、CLPSO算法[9]、DE算法[10]和PSO算法[11]对5个基准函数求解。测试函数的表达式、搜索范围和理论最优值见表1。该测试函数具有多样性,可以全面地反映DE-PSO算法的搜索性能。

表1 基准函数

为了验证DE-PSO算法的寻优性能,将DE-PSO算法同其他4种智能算法进行测试函数仿真对比。DE-PSO算法参数设置为c1=c2=2;wmin=0.4,wmax=0.8,F=0.5,Pc=0.9,Pr=0.99；CLPSO算法、PSOGA算法和PSO算法参数设置为c1=c2=2,w=0.8；DE算法参数设置F=0.5,Pc=0.9。对于每种算法,种群个数NP=30,最大迭代次数Gmax=2 000。为了避免随机性带来的影响,所有算法在每个测试函数上均独立运行30次,采用最优值、平均值、最差值和方差4个指标衡量各种算法的性能,实验统计函数仿真结果如表2所示。

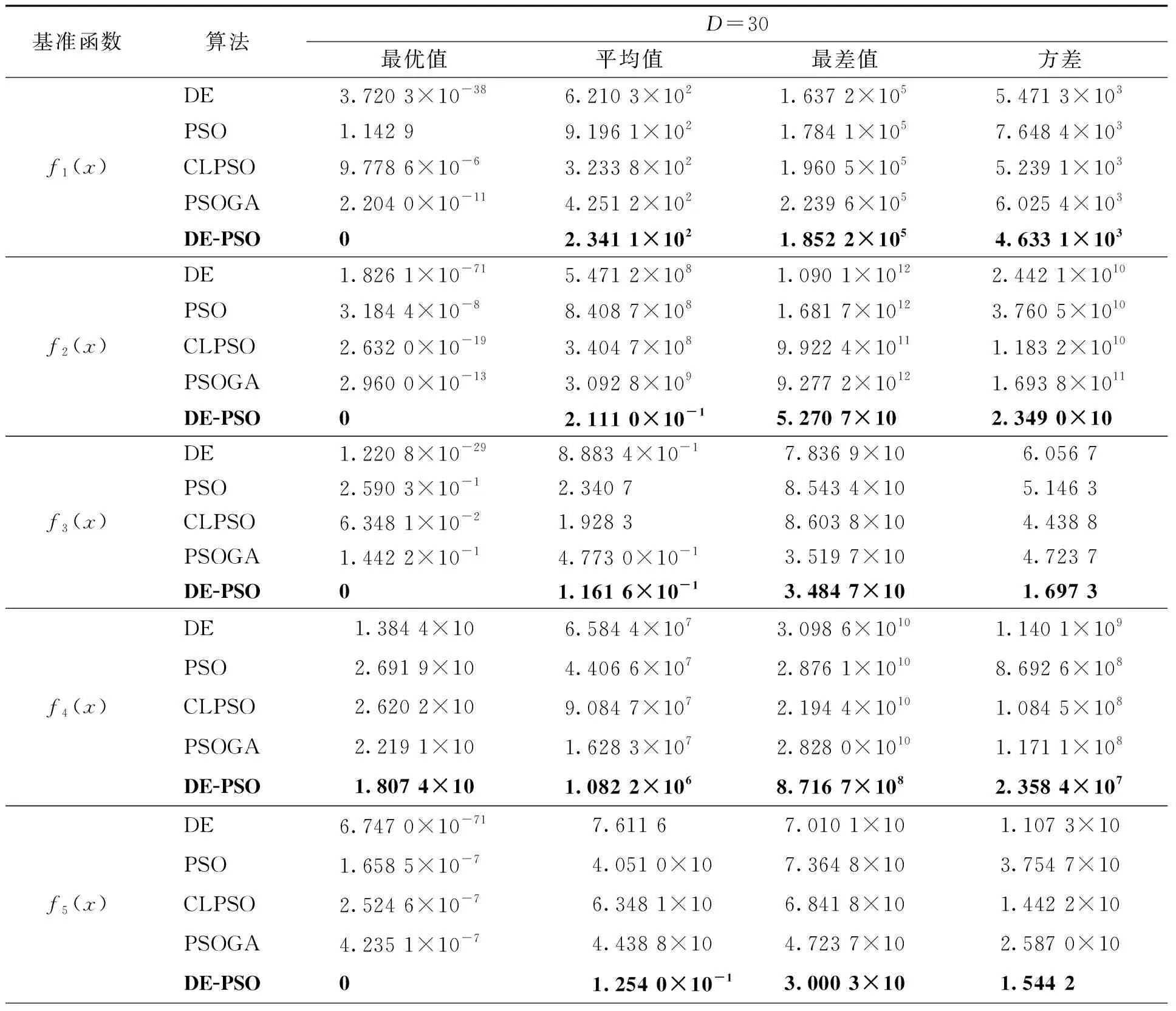
表2 低维时，5类智能算法对不同基准函数的测试结果

从表可见，DE-PSO算法对于求解低维函数或者高位维函数都有良好的性能,其中对于低维函数f1、f2、f3和f5，无论是最优值、最差值、均值还是方差值都优于其他4种智能算法的。对于f4,DE-PSO算法略小于DE算法,但它在搜索性能方面比其他算法要好得多，意味着DE算法适用于解决这些函数。当维度为50维和100维时,函数f1、f2、f3、f4和f5无论是最优值、最差值、均值还是方差值都优于其他4种智能算法的,具有很强的鲁棒性(表3)。整体比较来说DE-PSO算法整体性能最好,稳定性较强。

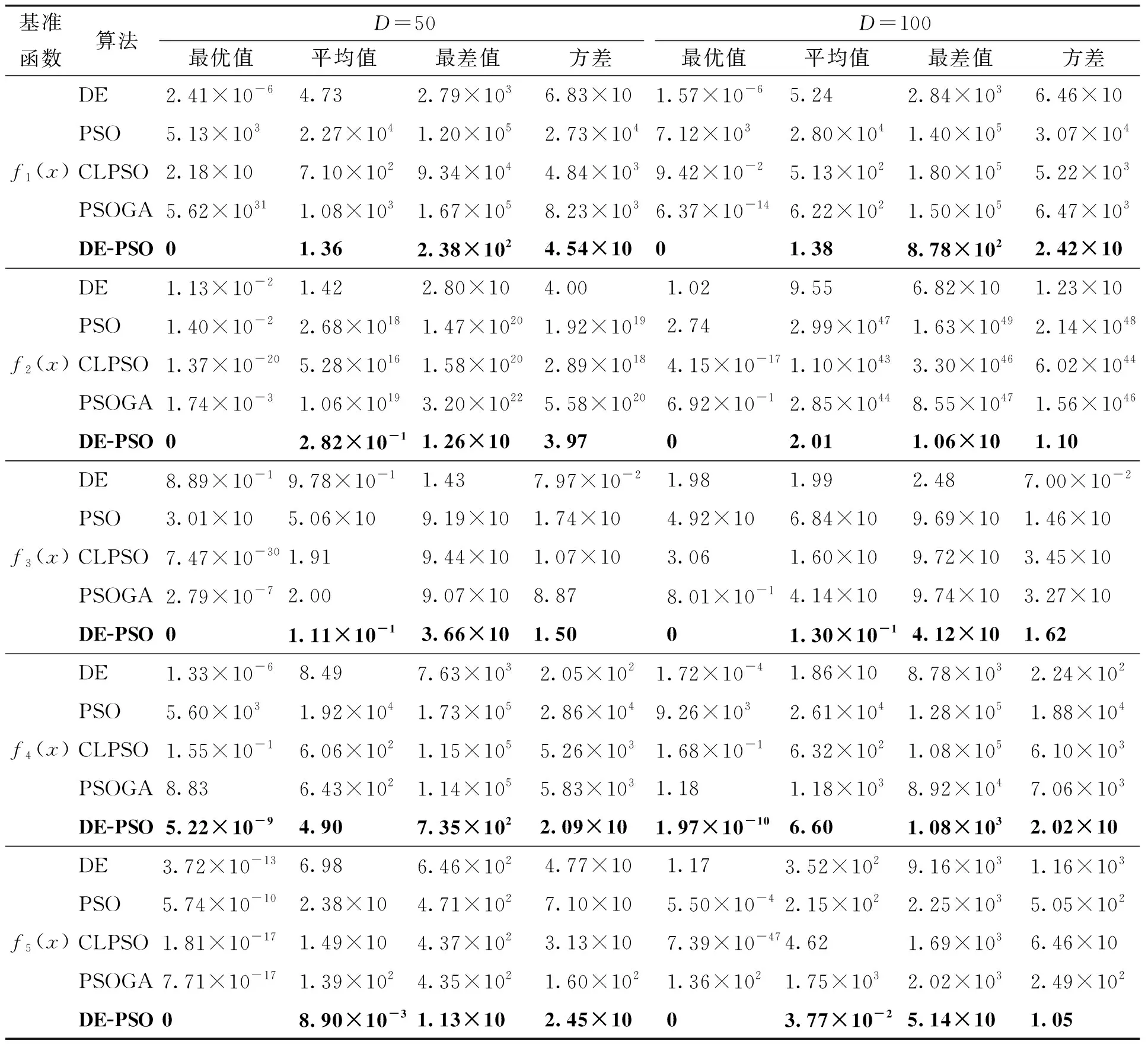
表3 高维时，5类智能算法对不同基准函数的测试结果

5种智能算法求解5个测试函数的最优收敛曲线分别如图1—5所示。

图1 f1收敛曲线

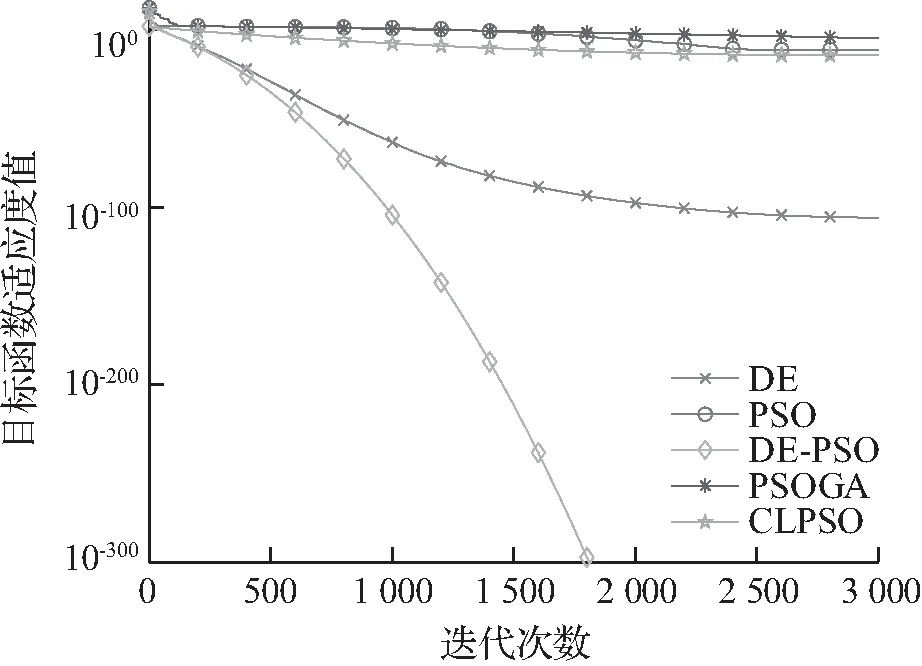
图2 f2收敛曲线

图3 f3收敛曲线

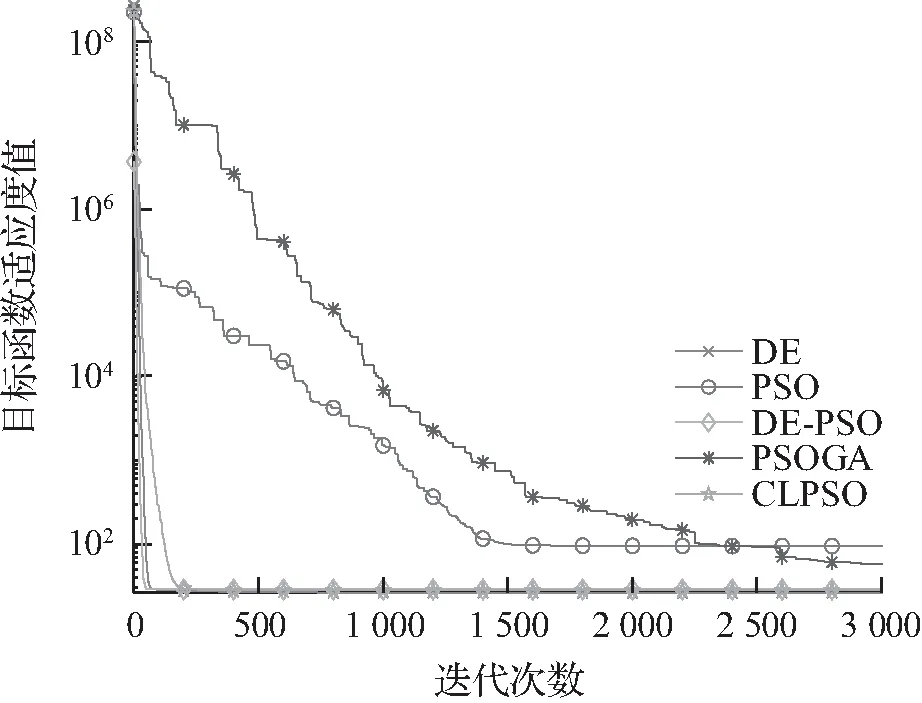
图4 f4收敛曲线

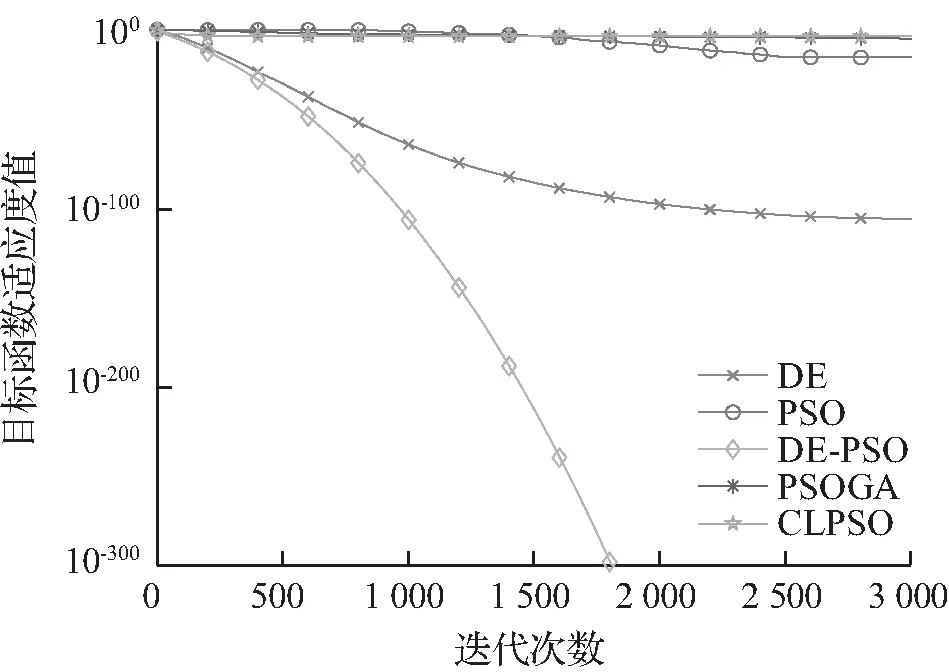
图5 f5收敛曲线

从图1—5可见,随着测试函数特性的变化,5种智能算法收敛曲线随之也变化。无论是收敛速度还是搜索精度,DE-PSO算法明显优于其他4种算法，因此,DE-PSO算法具有更全面的优势。

4 微电网多目标优化调度模型

4.1 微电源数学模型

4.1.1 光伏发电系统模型

光伏发电是利用光生伏特效应,将太阳能转换成电能的系统,发电装置的功率主要受温度、光照等因素的影响。因此,建立光伏电池输出功率模型如式(13)所示。

(13)

式中:PSTC为标准状态(1 000 W/m2,温度为25℃)下的额定功率；GC、GSTC分别为实际光照强度和标准条件的光照强度；TC、TSTC分别为工作温度和标准温度。

4.1.2 风能发电系统模型

风能发电系统主要由风力涡轮机组成,其输出功率受风速、风力、涡轮机的位置等因素的影响。因此,风力涡轮机输出功率模型如式(14)所示。

(14)

式中:PWT,rate为风机额定输出功率；ui、uo、ur分别为切入风速、切出风速、额定风速。

4.1.3 储能装置模型

储能装置可以有效保证微电网的稳定运行,也可以实现削峰填谷的功能。储能系统存储电量与蓄电池的荷电状态(state of charge, SOC)相关,其在t时刻充放电模型如式(15)所示。

(15)

式中:fSOC(t),fSOC(t-1)分别为t,(t-1)时刻蓄电池的剩余的电量；Pk(t)代表储能装置的充放电功率,Pk(t)>0为充电状态,Pk(t)≤0为放电状态；ηc,ηd表示充、放电效率。

4.1.4 柴油发电机模型

柴油发电机的发电成本采用二次函数表达式如式(16)所示。

CDE=a+bPDE+cPDE2,

(16)

式中:CDE是燃料成本；PDE是柴油发电机的发电功率；a,b,c分别为燃料成本的系数。

4.2 目标函数

以经济成本最低和环境效益最好为目标函数。经济成本主要包括运行成本、燃料费用和与大电网之间电量交换成本。网环境成本包含微电源的污染气体(CO2、NOx、SO2)治理费用。以经济成本、环境治理成本为最小建立目标函数:

F=min(φF1+μF2),

(17)

式中:F为总运行成本;F1、F2分别为经济成本、环境治理费用;φ、μ取值都为0.5。

目标1 经济成本：

(18)

式中:T为一个调度周期;N为分布式电源的种类;Ci,f、Ci,m分别为各微电源的燃料系数、运行管理费用;Pi,t为第i种微电源的输出功率;CGRID,t为t时刻电价;PGRID,t为t时刻与电网的交互功率。

目标2 环境成本:

(19)

式中:M为污染物的种类;βi,h为分布式电源i排放污染物h的排放系数;αi,h为分布式电源i排放污染物h的治理费用。

4.3 约束条件

① 功率平衡约束条件为

(20)

② 微电网与主网的交互功率约束为

(21)

③ 各微电源的出力约束为

(22)

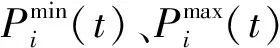
④ 蓄电池的约束条件为

fSOC,min≤fSOC,t≤fSOC,max,

(23)

式中fSOC,max、fSOC,min分别为蓄电池荷电状态的上、下限制。

5 基于DE-PSO算法的微电网能量调度

5.1 算例仿真参数

本文主要研究并网型微电网,采用MATLAB为仿真平台,GRID表示电网,种群大小30,算法参数设置如前文,与大电网的交互功率为200 kW。以广东某地区典型日为研究对象,预测功率如图6所示,各微电源的运行参数,污染物治理费用分别见表4和表5。

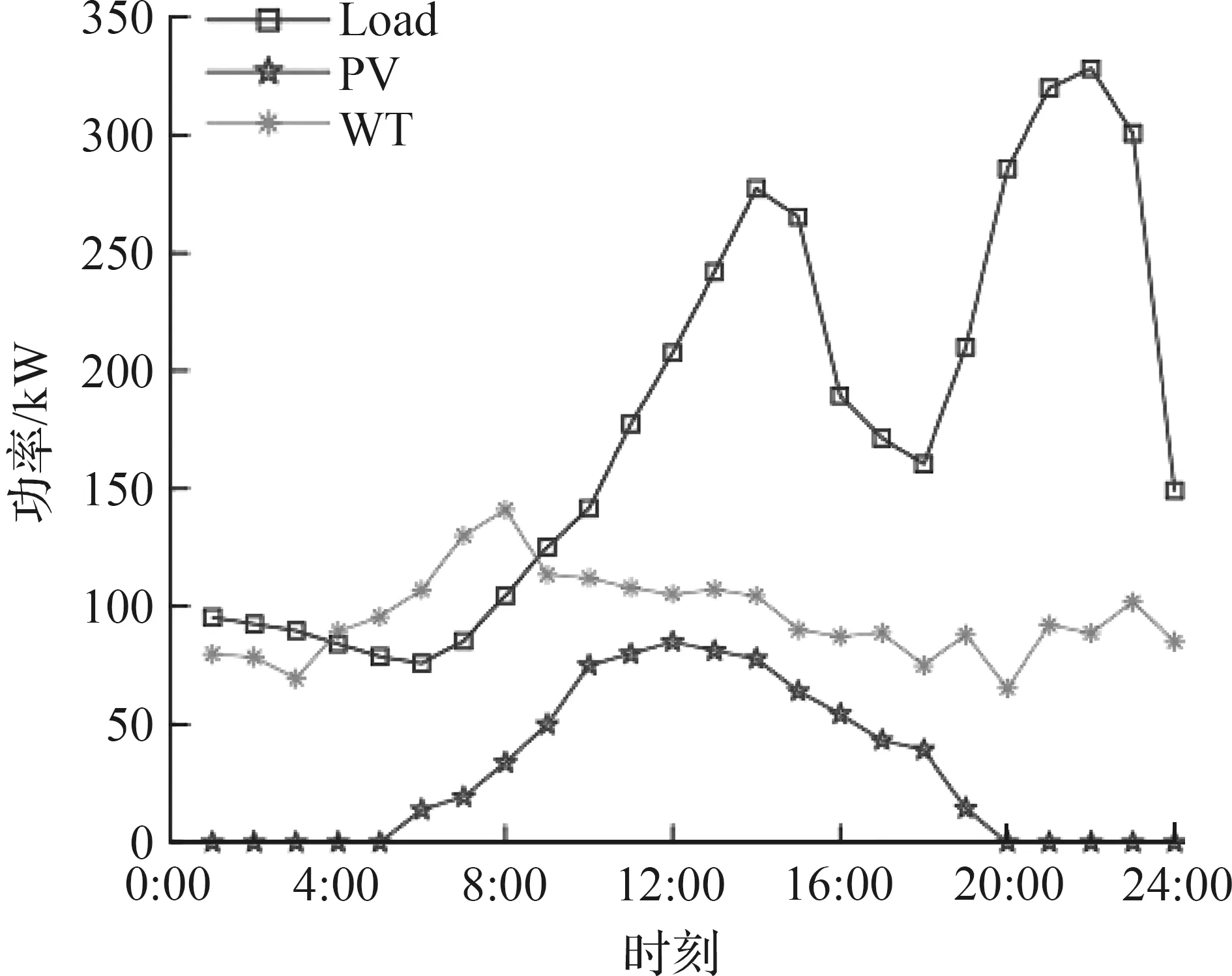
图6 负载、PV、WT预测功率

表4 各分布式电源参数

表5 污染物的治理费用

微电网并网运行时,电网电价采用实时电价,不考虑售电情况。各时段实时购售电单价见表6。

表6 各时段实时购售电单价

5.2 调度结果分析

本文设定2种不同的方案采用DE算法、PSO算法和DE-PSO算法求解,其结果如下:

5.2.1 储能装置不参与调度

当储能装置不参与调度时,各分布式电源的出力情况如图7所示,总成本如图8所示。

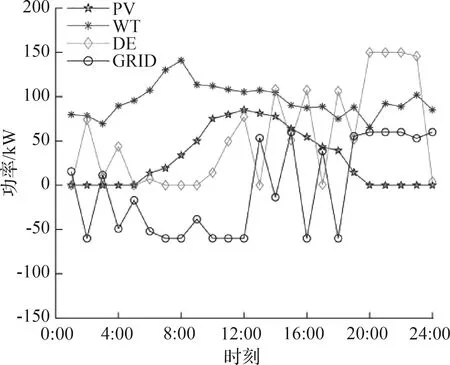
图7 无储能时各电源输出功率

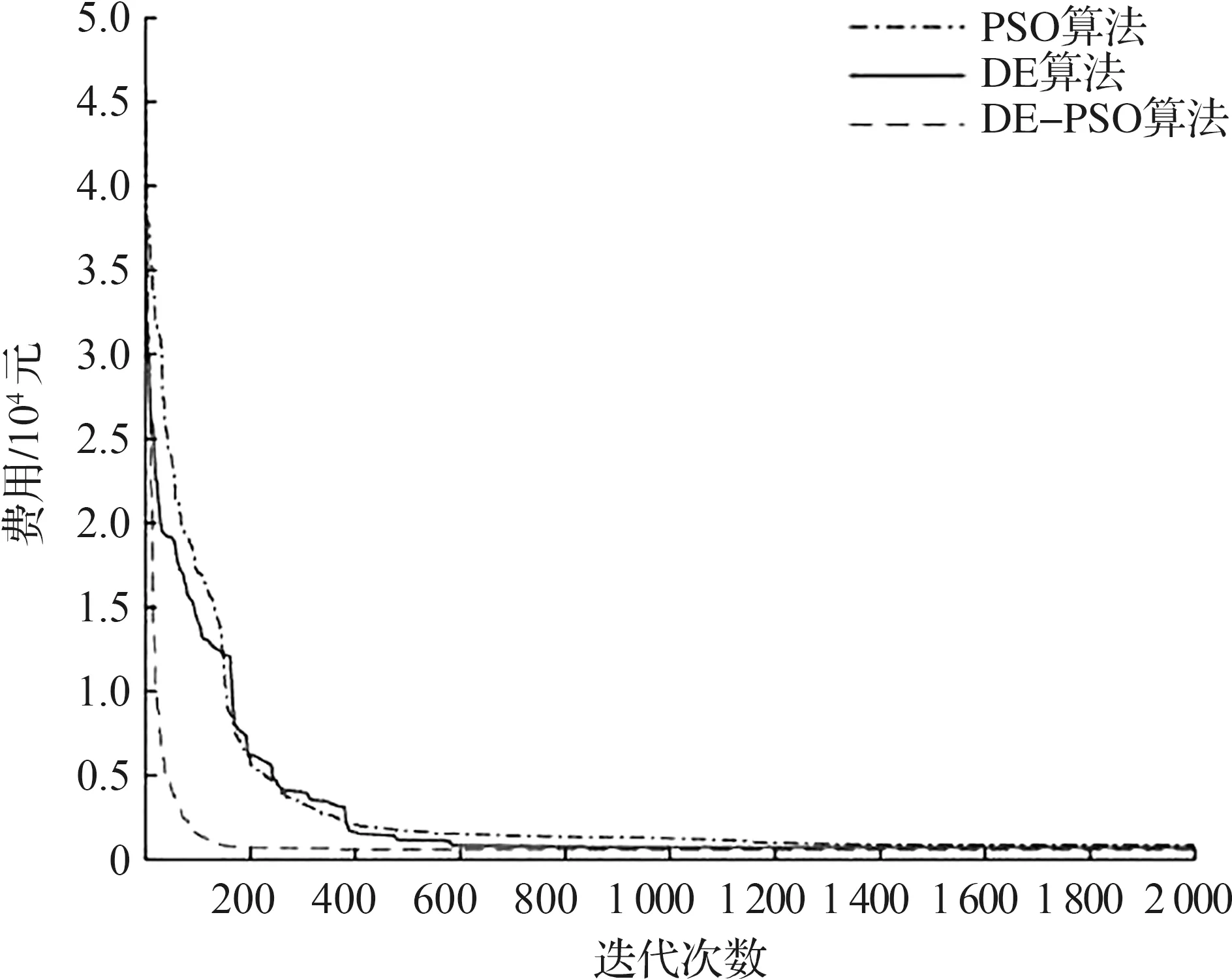
图8 无储能时运行总费用

蓄电池不参与调度时,风能和太阳能属于清洁能源优先被考虑使用,如图7所示。柴油发电机、光伏电池和风力发电机共同出力满足居民负荷的要求,当负荷需求高时,向主网购电,以满足居民的负荷需求。图8显示出DE-PSO算法的收敛速度和精度优于DE算法和PSO算法的,有效降低总的运行花费。

5.2.2 储能装置参与调度

当储能装置不参与调度时,各分布式电源的出力情况如图9所示,总成本如图10所示。

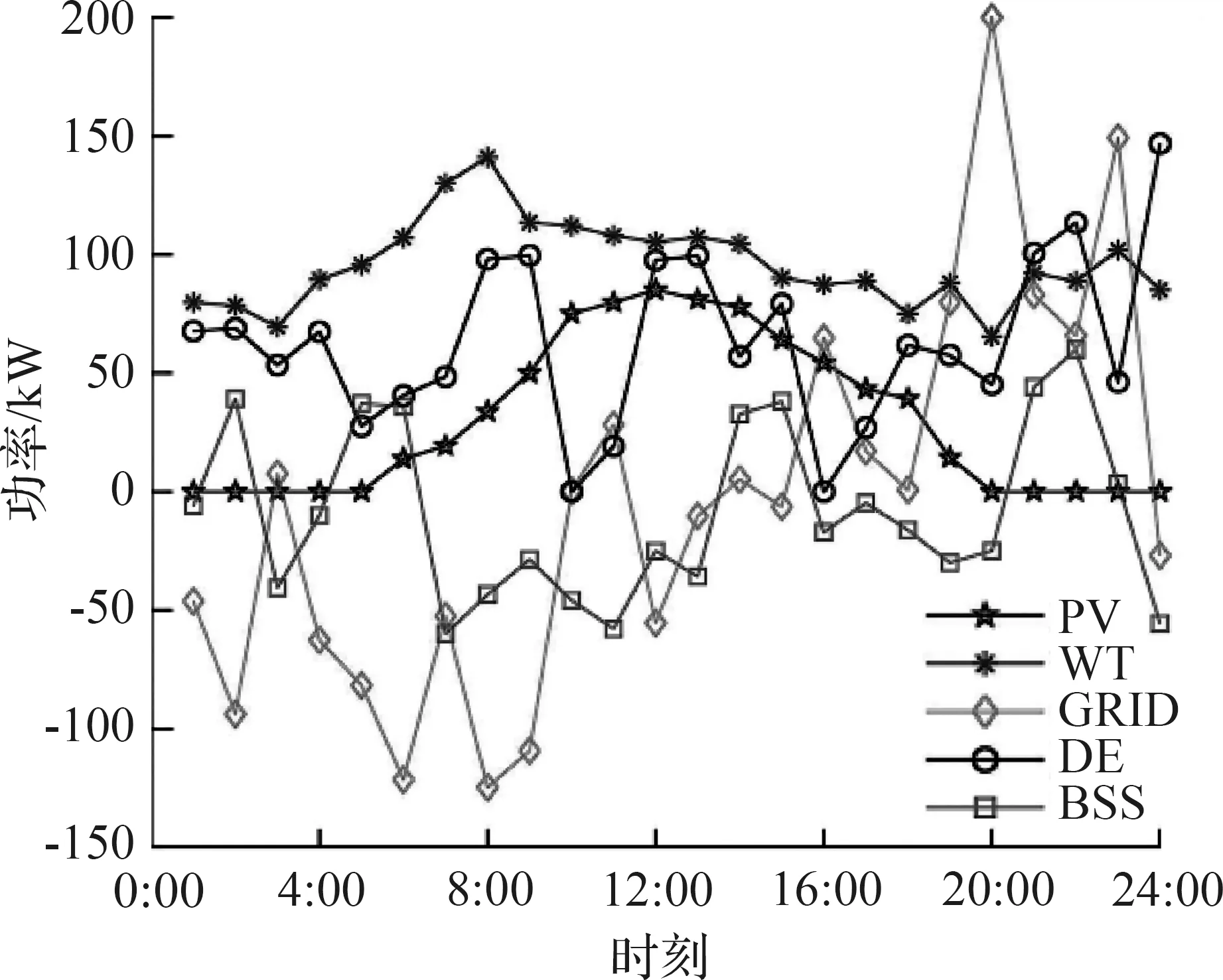
图9 含储能时各电源输出功率

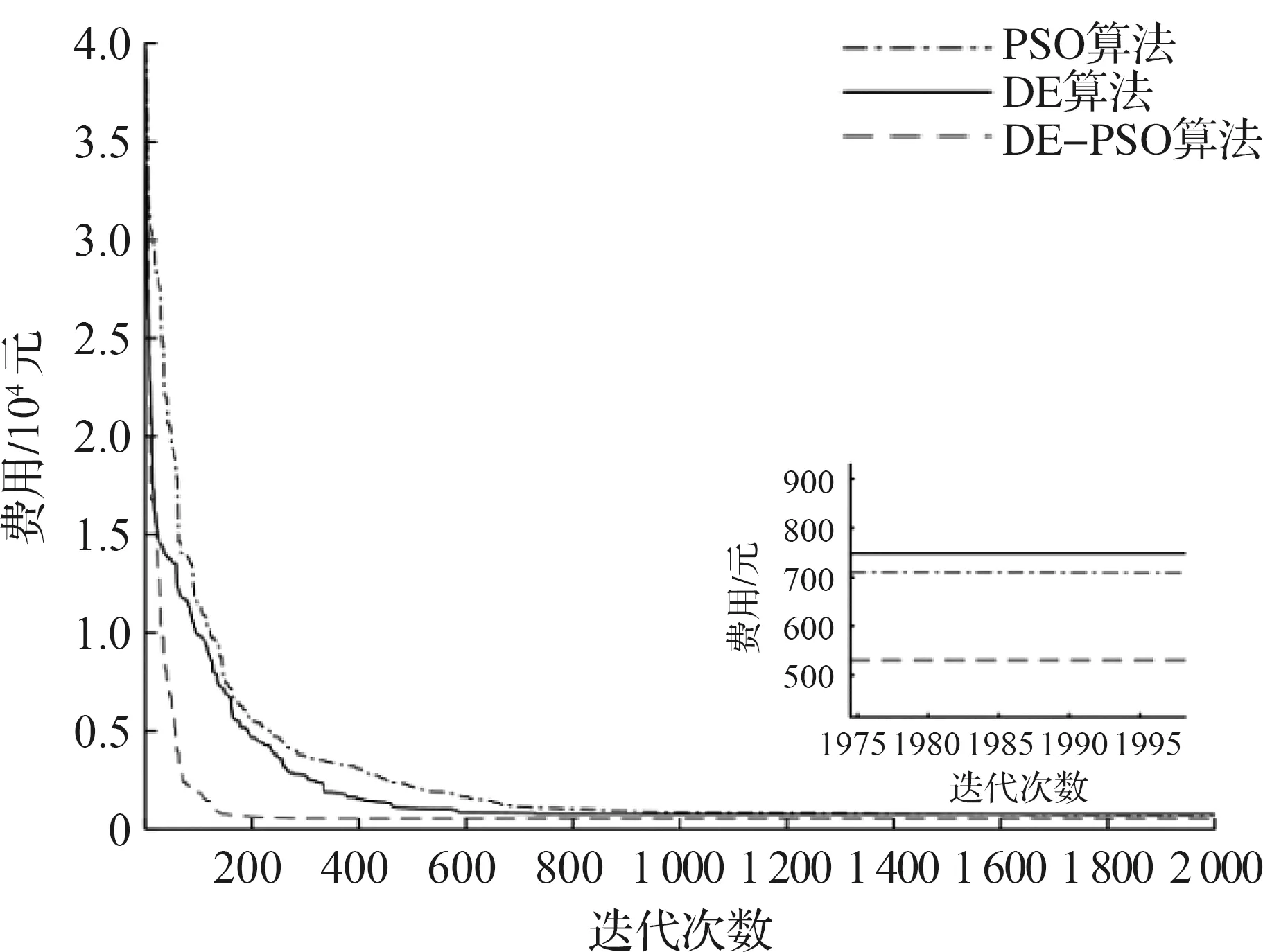
图10 含储能时运行总费用

蓄电池参与调度时,有利于缓解放电时引起的功率波动,对电网放电起到缓冲作用,有利提高系统的稳定性,且可以减少用电损耗,从而达到节约成本的效果。如图9所示,蓄电池在1:00、7:00-13:00、16:00-20:00时一直处于充电状态,为用电高峰时期做准备,其余时间段蓄电池处于放电状态,缓解电网的放电压力。从图10中可以看出,有储能装置时,DE-PSO算法的收敛速度和精度优于DE算法和PSO算法的,有效降低总的运行花费。

5.3 算法对比

无储能装置时,各算法的寻优情况如图8所示,DE-PSO算法的收敛速度明显优于DE算法和PSO算法的,而对于收敛精度,3种算法同时求解本文建立的模型时,DE-PSO算法、DE算法和PSO算法总运行成本分别为591、832、753元,经济效益最大提升了28%,而收敛速度较其他算法提升了1.25倍。含储能装置时,各算法的寻优情况如图10所示,DE-PSO算法的收敛速度明显优于DE算法和PSO算法的,而收敛精度,3种同时求解本文建立的模型时,DE-PSO 算法、PSO算法和DE算法总运行成本分别为为530、708、747元,经济效益最大提升了29%,而收敛速度较其他算法提升了1.25倍。综上所述,无论是有无储能装置,DE-PSO算法的搜索精度和收敛速度都优于DE算法和PSO算法的,进一步验证了DE-PSO算法的有效性。

6 结论

针对DE算法的缺点，本文提出一种混合多重随机变异粒子差分进化算法(DE-PSO)。在DE-PSO算法基础上，分别引入不同的变异策略(粒子群差分变异策略、DE/current-to-rand/1变异策略)，同时采用一种简单的扰动策略有效解决了粒子因陷入局部最优而早熟收敛的问题。本末通过选取5个基准测试函数，对5类智能算法开展仿真实验，结果表明，DE-PSO算法具有较好的搜索精度和收敛速度，且明显优于其他4种智能算法的。此外，本文所提算法在微电网能量调度中也取得理想的效果，进一步说明本文算法的可行性和优势所在。