考虑层间剪应力的黏性土非极限主动土压力数值解

马明, 李明东*, 张京伍,2, 朱丽萍

(1.东华理工大学 土木与建筑工程学院, 江西 南昌 330013；2.岩土力学与堤坝工程教育部重点实验室, 江苏 南京 210098；3.东华理工大学 水资源与环境工程学院, 江西 南昌 330013)

0 引言

刚性挡土墙应用非常广泛,计算墙背土压力是关键设计环节。在实际工程中,很多工程会存在人为限制墙体位移,也有一些工程无法达到极限位移,此时作用在当墙上的土压力为非极限土压力[1-4]。这种情况下如果采用极限状态下的经典土压力理论计算,所得主动土压力计算结果就会偏小,挡土结构的安全系数就会被高估，因此,建立考虑墙体实际位移的主动土压力计算方法很有必要。

非极限主动土压力的计算方法包括2类：第1类方法基于模型试验结果,利用函数拟合方法获得主动土压力随墙体位移的变化规律[5]；第2类方法认为土体强度参数随墙体位移渐进发挥,通过非极限土体强度参数构建主动土压力与墙体位移的关系[6]。其中,后者具有清晰的物理力学模型,结果具有普适性,成为非极限土压力研究的主流方法。平移模式(T模式)作为刚性挡墙典型的位移模式,其主动土压力计算方法已有诸多研究。对于无黏性土：卢坤林等[7]基于卸荷应力路径的三轴试验结果,推导了土体强度参数与位移的函数关系,初步得到了无黏性土的非极限土压力计算方法；Zhou等[8]解决了土拱效应影响下主应力偏转的问题；刘忠玉等[9]、陈奕柏等[10]考虑了层间剪应力对土压力分布的影响；陈建旭等[11]综合前人研究成果推导了多因素影响下无黏性土的非极限主动土压力计算方法,可以很好地与模型试验结果吻合。对于黏性土：涂兵雄等[12]、徐日庆等[13]利用坐标平移法分别推导了黏性土在土拱效应和位移影响下的主动土压力计算方法；娄培杰[14]在二者基础上进一步得到了土拱效应影响下黏性土的非极限主动土压力计算方法；陈建功等[15]基于变分法,得到了曲线滑裂面下考虑黏性土张拉裂缝的主动土压力计算方法。无黏性土的主动土压力研究表明,不考虑层间剪应力会导致主动土压力强度分布计算结果不准确,合力作用点偏移[16],然而,尚未见考虑层间剪应力的黏性土主动土压力计算方法。

本文完善了黏性土非极限土体强度参数的计算方法，并在黏性土的力学模型中引入了层间剪应力，建立了相应主动土压力强度、合力及作用点的数值计算格式。与模型试验结果、现有解析解及经典土压力解进行了对比，证实了本文解的优越性。以期新的计算方法能准确计算主动土压力，为实际工程设计提供便利。

1 非极限主动土压力数值解的相关因子

1.1 内摩擦角与位移的关系

徐日庆等[13]假定土体的径向应力与径向应变具有双曲线关系,采用如图1所示坐标平移法导出了黏性土内摩擦角φm与墙体位移的函数关系：

图1 坐标平移法示意图

(1)

K0c=0.95-sinφ，

(2)

式中K0c为黏性土的静止压力系数。

为了进一步完善K值的计算,按照定义推导如下：

(3)

K=K0s=1-sinφ。

(4)

1.2 墙土摩擦角与位移的关系

假定墙土摩擦角δm随墙体位移的发挥程度与内摩擦角φm的发挥程度相等,得

δm=ξφm

(5)

式中ξ为极限主动状态下,实测墙土摩擦角δ与实测内摩擦角φ之间的比例系数,若无实测值可取2/3[17]。

1.3 黏聚力与位移的关系

黏聚力cm、墙土间的黏聚力cwm与位移的关系可由式(6)确定[13]。

(6)

式中：c为极限状态的黏聚力；cw极限状态下墙土之间的黏聚力,约为c的2/3。

2 非极限主动土压力数值解的获取方法

2.1 考虑土拱效应的土体应力状态分析

土拱效应会引起土体内应力重分布,是土压力呈非线性分布的主要原因[18]。为了定量研究土拱效应对主动土压力的影响,通常假定一定形状的拱迹线[19-20]。研究表明拱迹线的形状对计算结果的影响较小[21],故本文假定小主应力拱迹线为圆弧线,如图2所示,圆心在O点,极坐标方程为

图2 土拱及土体应力分析

ρ(ψ)=R，

(7)

式中：ψ为极角；R土拱半径。

该拱迹线的起点在墙土接触面上,终点位于圆心O与滑裂面连线的延长线上。对应墙面处的大主应力转角θ1m与滑裂面处的大主应力转角θ2m可由式(8)确定。

(8)

图3 墙后土体的应力莫尔圆

(9)

式中：ψm为土拱任意一点的大主应力与水平方向的夹角,取值范围为(θ1m,θ2m)；Kam为朗肯主动土压力系数,由式(10)确定。

(10)

2.2 侧土压力系数的计算

(11)

将水平向应力除以平均竖向应力可求得黏性土的主动侧土压力系数K1m：

(12)

2.3 层间剪应力摩擦系数的计算

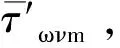
(13)

(14)

2.4 主动土压力数值迭代解

朱建明等[22]将黏性土的K1m通过无黏性土的侧土压力系数K1ms转化为式(15),解决了K1m受深度影响难以积分的问题。

(15)

本文将剪应力系数K2m参照式(15)转化为式(16),由于剪应力τωνm涉及微分问题,其微分形式为式(17),此法在消去K2m的同时又引入了dσ0这一新的微分形式,故无法通过积分得到显示解。因此,在黏性土力学模型中引入层间剪应力后,必须采用数值解法求解土压力。

(16)

(17)

本数值解将土体按步长Δy水平条分,如图4所示。假定步长范围内计算参数相同,以第i层土体为例,主动侧土压力系数为K1mi,层间剪应力系数为K2mi,滑裂面倾角为βmi。这样,就可以按式(18)确定第i层条分体墙面处的法向力σωmi、墙面处的切向力τωmi、滑动面上的切向力τsmi以及层间剪应力τωνmi。

图4 土体水平条分及受力分析

(18)

对第i层水平条分体ABCD做静力平衡分析,由水平方向合力为0可得

σωmiΔy-τωνm(i+1)Li+1+τsmicotβmΔy+τωνmiLi-σsmiΔy=0。

(19)

由竖向合力为0可得

σνmiLi+ΔGi-σνm(i+1)Li+1-τωmiΔy-τsmiΔy-σsmicotβmΔy=0。

(20)

式中：ΔGi为第i层水平条分体的自重,由式(21)确定；Li为第i层水平条分体的上界面宽度,由式(22)确定；Li+1为第i层水平条分体的下界面宽度,按式(23)计算。

(21)

Li=(H-iΔy)cotβmi。

(22)

Li+1=(H-(i+1)Δy)cotβmi。

(23)

联立式(18)—(23)可建立竖向应力σνmi的迭代格式，

(24)

式中：λ1mi、λ2mi及λ3mi为迭代过程中的组合系数,由式(25)确定。

(25)

对墙顶临界深度以下至墙底临界深度以上水平条分体的主动土压力求和,即可得到主动土压力合力，

(26)

式中：a为临界深度处的i值,可由式(27)求得；b为墙底临界应力处的i值,即式(24)跌代至0时的i值。

(27)

主动土压力对墙踵产生的倾覆力矩可以由式(28)求得。

(28)

用倾覆力矩除以水平向的土压力合力,再加上墙底临界应力处至墙踵的距离,就可求得主动土压力合力作用点位置，

(29)

通过以上工作,建立了黏性土非极限主动土压力的数值迭代格式。为了便于实际工程应用,可根据涂兵雄等[12]、周应英等[23]及岳祖润等[24]的研究成果,先按式(30)确定βm,再按照本迭代格式求解非极限主动土压力的强度、合力、倾覆力矩及作用点。

(30)

3 模型试验对比

3.1 模型试验1

周应英等[23]通过模型试验测试了T模式下墙背直立、填土面水平的刚性挡墙在初始状态(η=0)和极限状态(η=1)主动土压力的分布情况,试验挡墙高达4.5 m,为足尺试验,所有试验参数均为校核过后的实测值,试验过程严谨，结果可靠,满足本文理论模型验证的精度要求。具体试验参数如下：墙体高度H=4.45 m,填土容重γ=14.27 kN/m3,内摩擦角φ=24.27°,墙土摩擦角δ=21.4°,黏聚力c=1.472 kPa,墙土之间的黏聚力cw=0.98 kPa,表面均布荷载q=0 kPa。

对本文解、试验值、解析解和朗肯解进行对比分析,主动土压力分布情况如图5所示。其中,解析解1[13]考虑了位移效应,解析解2[14]进一步考虑了土拱效应,本文解在二者基础上进一步考虑了层间剪应力的影响。经对比可见,考虑层间剪应力后,对于初始状态的主动土压力和极限主动土压力,本解法的计算结果与模型试验结果均最为契合。

图5 本文解与模型试验、其他解析解的土压力分布对比情况

3.2 模型试验2

杨斌等[25]利用模型试验测试了墙背直立、填土面水平的刚性挡墙在T模式下主动土压力随墙体位移的变化情况,试验中设置了4个不同的填土表面均布荷载,分别为q1=276.8 kPa、q2=208.2 kPa、q3=139.7 kPa，q4=71.1 kPa,研究了侧土压力由静止土压力逐步向主动土压力的发展过程,得到了挡土结构位移和主动土压力强度间的关系,试验设计及操作过程严谨,试验工况充分,可以较好的验证本文非极限主动土压力这一主题。具体试验参数如下：墙体高度H=1 m,填土容重γ=19 kN/m3,内摩擦角φ=27°,墙土摩擦角δ=18°,黏聚力c=13.7 kPa,墙土之间的黏聚力cw=9.13 kPa,挡墙极限位移s=4 mm。

图6为本文解与实测值的对比情况,可以看出4组模型试验实测值与本文计算值均较好吻合。另外,本文解反映的非极限主动土压力发展过程与试验结果相符,即随墙体位移增加,土体强度逐渐发挥,主动土压力强度逐渐减小,最终趋于稳定达到极限主动状态。

图6 不同位移下本文解和实测值土压力强度的契合情况

通过上述2例模型试验较好的验证了本文数值解的合理性与准确性,第1例验证了初始主动状态与极限主动状态下本文解计算主动土压力的准确性,第2例则验证了本文解计算非极限主动土压力的准确性。

4 结语

本文给出了T模式下黏性土层间剪应力的计算方法,建立了考虑层间剪应力的非极限主动土压力数值迭代格式。经与模型试验结果、已有解析解、朗肯解对比,表明本解法可以更为准确地计算主动土压力,反映主动土压力随墙体位移的发展过程,将其用于实际工程可提高计算精度。

本文数值解的求解思路,同样可用于解决转动变位模式下土体强度参数随深度变化的非极限土压力问题,期待这类土压力问题能够早日解决。