基于TDOA的楼层过渡区域优化定位方法
2022-09-19王佳钰陈仕林陈祝明
王佳钰,陈仕林,保 骏,陈祝明,刘 朋,张 瑞
(1.电子科技大学,四川 成都 611730;2.中移(成都)信息通信科技有限公司,四川 成都 610213)
0 引 言
近年来,随着无线传感器网络的发展,室内定位技术发展得越来越成熟,精度不断提高,应用室内定位技术来提供精确定位信息的场所越来越多。当前的室内定位技术普遍采用分楼层进行二维定位的方式。但在上下楼梯的楼层过渡区域,由于高度变化,通过二维定位解算出的定位精度不高、误差较大。
针对上述问题,本文提出了一种基于TDOA算法对楼梯间区域进行精确定位的方法,只需在过渡区域增设一个基站,就能够有效地解决楼层过渡区域的定位问题。
1 楼层过渡区域的基站布设
当前常见的楼层结构如图1所示。两楼层之间的过渡区域由两楼梯梯段、一楼梯平台与栏杆扶手组成,两梯段左右错开。为了提高楼梯间定位的精度,只能增加楼梯间内的定位基站数量;但如此一来,不仅定位成本提升,多基站定位加上非视距环境等问题,也使得定位精度不高,在楼梯间区域的定位不够精确。
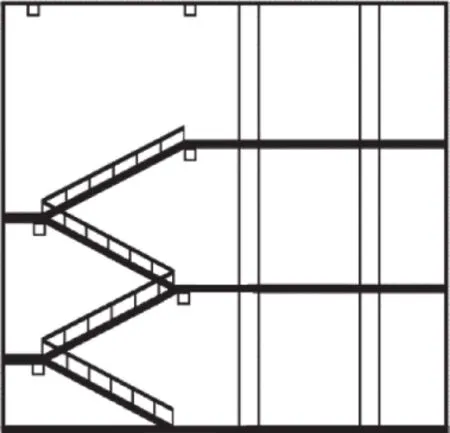
图1 常见的楼层结构
为了提高楼层过渡区域定位的精度,本文提出了一种新的楼层过渡区域定位方法。以图1的剪刀型楼梯为例,用空心矩形方块表示在楼层过渡区域铺设的基站的位置。基站安装于两梯段转折交汇处的天花板上。因此,所有基站均位于同一竖直平面上(即楼梯扶手平面)。
楼梯间区域的立体视图如图2所示,取楼层间折返的楼梯梯段与楼梯平台部分,在两端扶手的正上方天花板放置用白色立方体表示的定位基站。可以看出,每一个梯段上方均有两基站,可以无遮挡地被覆盖到。除此以外,位于靠近楼层区域的基站也可以与楼层定位共用,如图2中的2号基站。
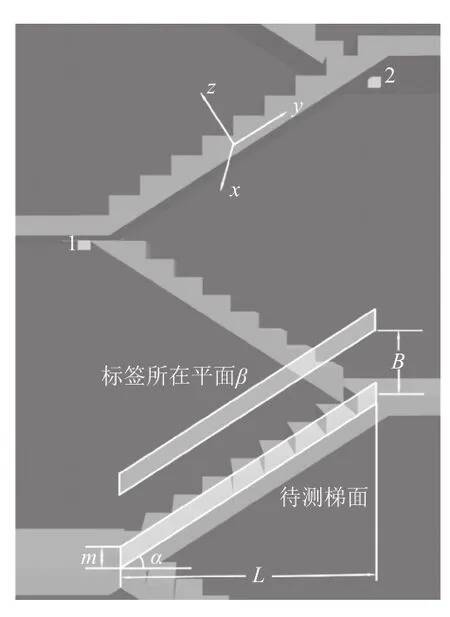
图2 楼梯间区域的立体视图
2 基于TDOA算法的楼层过渡区域定位方法
UWB定位中常用的算法包括到达角度(Angle-of-Arrival,AOA)算法、到达时间(Time of Arrival, TOA)算法以及TDOA算法等。相对于TOA算法中需要基站与标签的时间严格同步的要求,TDOA算法仅要求基站间时间同步,比TOA算法的要求更容易达成。对于利用TDOA算法进行定位的系统,基站会返回两基站收到信号的时间差,从而能够计算出标签到两基站间的距离差。传统的运用TDOA算法进行楼梯间定位的方式是在楼梯间内部放置多个定位基站,通过计算两两之间的信号到达时间差获得多组双曲线,取其交点为标签定位点。本文提出一种新的基于TDOA算法的楼梯间定位方法,具体原理如下:忽略踏面与踢面,将梯段视为长度为、宽度为、角度为的斜面,则斜面的斜率=tan。同时,设标签距离斜面的高度为已知的固定值,虽然标签可在梯段上任意位置,但为了计算方便,统一将其定位于梯段中线上。
建立沿梯面方向的坐标系如图3所示。对于待测梯面,1号基站与2号基站可以无遮挡地被覆盖到,因此调用1号基站与2号基站进行定位。首先通过基站获得两基站间的距离差Δ,从而可得到标签所在的以两基站为焦点的双曲面。由于标签距离斜面高度已知,可将标签视为在一平行于梯面且垂直距离为的矩形面上。如图3所示,双曲面与矩形面的交线即为标签所在的线段。取与中线的交点,即为标签所在点,从而可求得标签所在点的坐标。
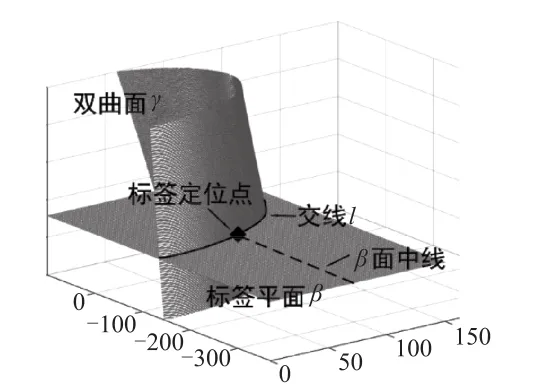
图3 面相交取定位点示意图
设1号基站与2号基站的坐标分别为(,,)、(,,),标签的空间坐标为(,,),从基站获得标签到两基站的距离差为:
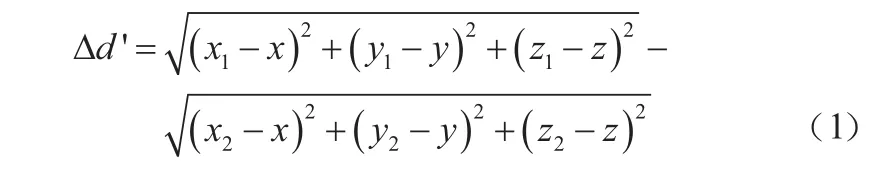
则有
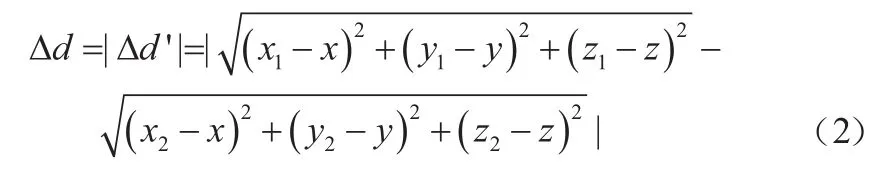
矩形面为:
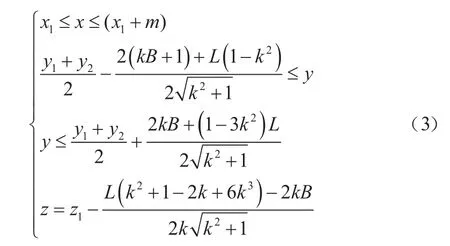
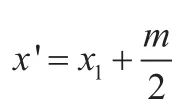
公式(2)对应的双曲面有单叶双曲面与双叶双曲面两种。单叶双曲面解算出的标签空间坐标只有一个;而双叶双曲面通常能够解算出两个不同的标签空间坐标,通过Δ的正负可判断出正确的空间坐标解。
通过以上计算,能够获得标签的空间坐标,从而可得出标签的运行轨迹。
3 仿真分析
对上节所述算法进行MATLAB仿真。由于标签的实际高度未知,因此需首先设定标签的高度为一定值。设定楼梯模型如下:取一阶楼梯的参数为长30 cm、高15 cm、宽150 cm,每个梯段共14阶楼梯,即总长度=420 cm,总高度为210 cm。梯面倾斜斜率=0.5,设定标签高度=120 cm。
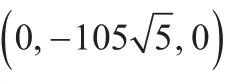
由于标签携带者并不一定在梯段中线上,而本定位方法在计算时将标签视为位于梯段中线上,因此标签与梯面中线的左右偏差必然对定位误差有影响;且一般来讲,标签偏离梯面中线越远,误差越大。由于本方法的目标是定位标签在轴上的位置,因此仅考虑标签真实坐标与解算出的空间坐标在轴上的误差。标签卡的真实坐标为(,,),通过本方法解算得到的标签坐标为(,,),则定位误差为|(-)|。
考虑几种常见的标签卡佩戴方式:胸牌、挂牌、头顶、脚底。以180 cm身高为标准,设定胸牌标签的固定高度=140 cm,挂牌标签的高度=120 cm,头顶标签的高度=180 cm,脚底标签的高度=0 cm。
由于标签佩戴者的身高差异,标签高度与设定高度可能存在差异,如图4所示,其中基站平面表示基站所在的垂直平面。
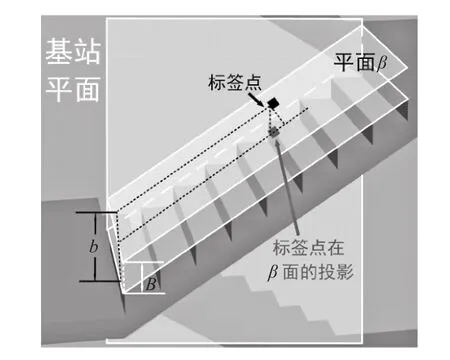
图4 标签实际高度与设定高度差异示意图
从梯面上取随机点,仿真400次,每种佩戴方式下不同的标签卡高度与设定高度偏差时的误差均值和标准差如图5所示。由图5可知,定位误差与标签佩戴方式无关,仅与标签卡实际高度与设定高度的差值相关。与的差值与误差的关系如图6所示。

图5 不同标签佩戴方式下的定位效果
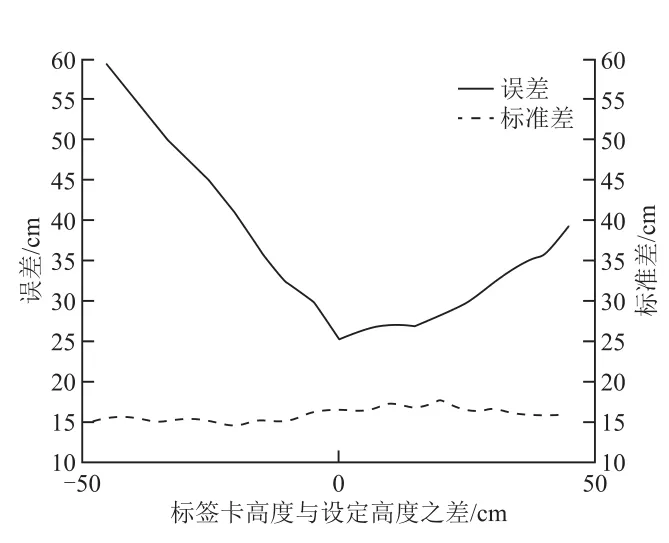
图6 标签卡实际高度和设定高度之差与误差的关系
由图6可知,定位误差与标准差整体上随标签卡实际高度与设定高度之差的增加而变大。标签卡实际高度低于设定高度时,其误差增长的速度较快。当标签卡实际高度低于设定高度10 cm或高于设定高度30 cm以上时,定位的误差均值较大,定位效果明显变差。
由于标签卡在梯面水平方向上位置不定,因此标签与基站所在的垂直平面(以下简称“基站平面”)的偏差对定位误差可能存在影响。标签与基站平面的偏差示意图如图7所示。
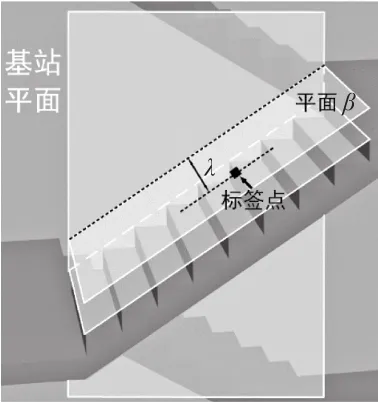
图7 标签与基站平面的偏差示意图
标签卡定位效果与标签和基站平面的偏差的关系如图8所示。经仿真验证,由于仿真时仅考虑了沿梯面方向的偏差,因此以基站所在的垂直平面为基准,标签距离该平面的偏差与误差没有明显关系。
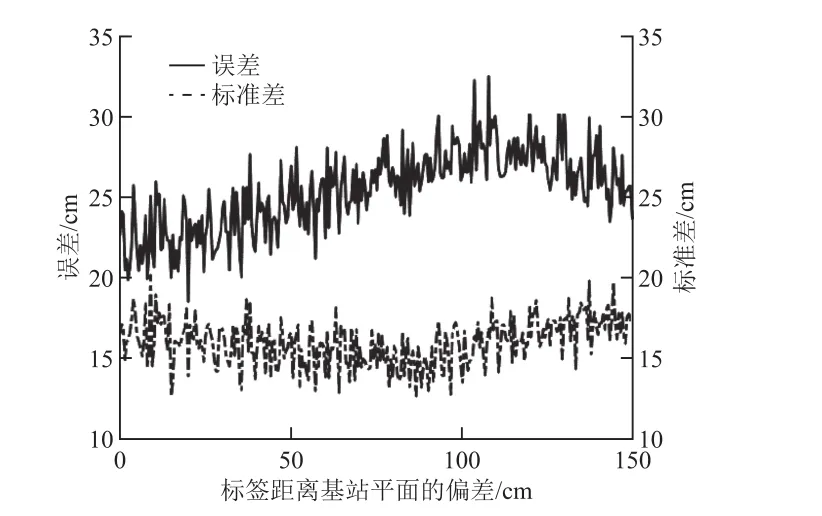
图8 标签距离基站平面的偏差与误差的关系
标签距离基站平面的最大偏差与误差的关系如图9所示。标签距离基站平面的最大偏差越小,在梯面长度一定的条件下,整个梯面就越趋近于一条线。由此可知,定位误差与标准差随标签距离基站平面的最大偏差的增加而变大,且几乎线性相关。
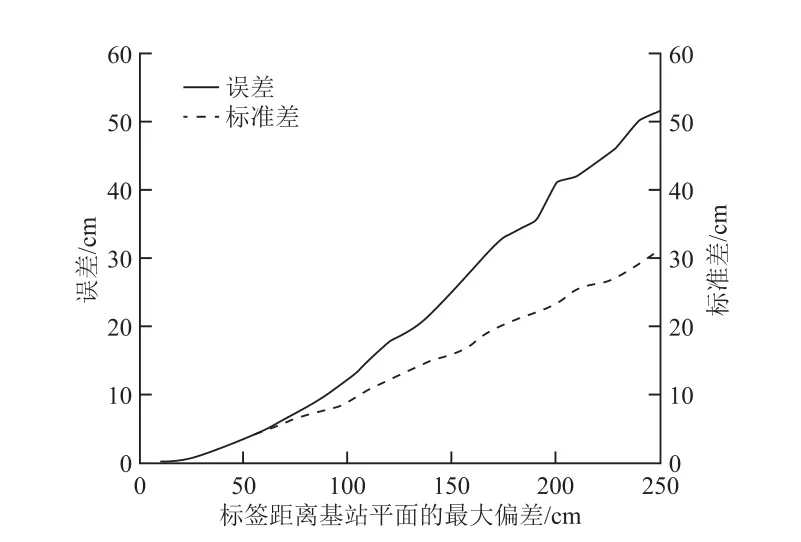
图9 标签距离基站平面的最大偏差与误差的关系
标签卡定位效果与梯面斜率的关系如图10所示。在梯面长度和梯面宽度一定的条件下,梯面斜率越大,整个梯面斜面的长度就越长,斜面越趋近于一条线。由此可知,定位误差与标准差整体上随斜率增加而降低。当梯面斜率低于0.5时,定位误差的均值明显增大,定位效果明显变差。
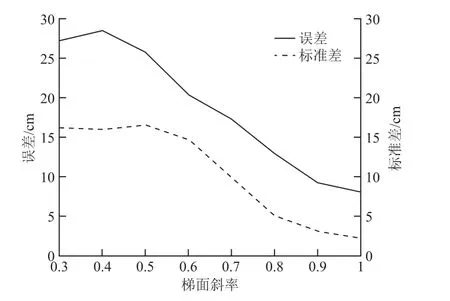
图10 梯面斜率不同时的定位效果
标签卡定位效果与楼梯总长度的关系如图11所示。由于梯面长度越长,斜面长度也越长,两基站间的距离就越大。由此可知,定位误差与标准差均随楼梯总长度增加而降低,当总长度低于400 cm时,定位效果明显变差。
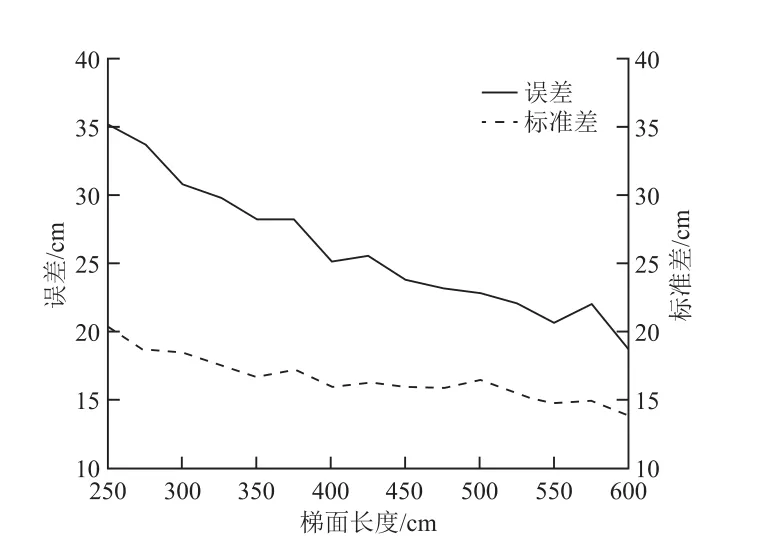
图11 梯面长度不同时的定位效果
4 结 语
本文提出了一种基于TDOA算法的楼层过渡区域优化定位方法。通过MATLAB仿真分析了楼层过渡区域的楼梯长度、角度、标签高度、与基站平面的偏差等因素会对定位精度产生的具体影响。在实际应用中,应综合考虑以上各项参数进行定位系统的设计。本文弥补了当前对层间过渡区域双曲线定位方法与精度的研究缺失,对工程应用有一定的指导作用。
