FAST工程主动反射面健康监测系统温度信号多元回归估测
2022-09-17王清梅李振伟楚敬敬
孙 晓,王清梅,李振伟,乔 峰,楚敬敬
(1. 青岛科技大学自动化与电子工程学院,山东 青岛 266061;2. 中国科学院国家天文台,北京 100101)
结构健康监测是通过布设大量传感器,监测并评估结构当前状态的一种技术,在工程结构的安全监测中有广泛应用。500 m口径球面射电望远镜是具有主动反射面的大型钢结构工程[1]。文[2]讨论了FAST结构受力复杂性,由于结构特殊、空间跨度大且环节众多,在观测过程中主动反射面受控变形导致结构受力复杂,为保证其安全工作,建设了主动反射面健康监测系统,通过监测关键结构的应力和环境信息,实现FAST的健康状态评估。文[3]指出,在索网施工过程中,该系统监测的圈梁实时应力最大约60 Mpa,始终小于设计安全值201.5 Mpa,保持在安全范围内,并指出温度信号对应力分析的重要性。
在FAST工作过程中,索网主动变形使结构受力更为复杂,以2019年7月的监测数据为例,所有圈梁格构柱测点应力最大值为137.37 Mpa,最小值为-135.88 Mpa,仍处于安全范围内,但部分测点应力变化范围较大,应力变化最大的测点极差为167.17 Mpa。在望远镜后续工作中,应力的监测对结构实时健康状态评估、长期疲劳损伤评估等具有重要意义。
大型工程结构空间尺寸大,不同部位温度升高不同,温差与温度效应会使结构应力发生较大变化。文[4]指出,FAST结构中,温度荷载对圈梁结构的刚度起控制作用,分布测点温度信息是评估结构状态的重要依据[5]。FAST应用了416只光纤Bragg光栅(Fiber Bragg Grating, FBG)应变传感器[6]监测应力,共包含圈梁及格构柱应力测点100只,主索索力测点316只,虽然测点分布位置不同,但所有测点需根据不同测点的实际温度补偿应变传感器的温度应变交叉敏感问题。文[7]进一步讨论了分离结构应力的温度效应对状态评估的必要性,温度信息缺失将直接导致测点应变信息不可靠。
实际工程现场环境复杂,大量传感器长期工作,传感器及数据通道存在一定故障率。检修发现,FAST主动反射面健康监测系统已有个别光纤光栅解调仪出现故障,且存在数只传感器数据异常,已确定异常测点数目约为5%,部分监测数据无法正常获取。但受限于现场施工条件,以及部分测点安装位置特殊,故障传感器无法第一时间修复,数据的缺失将导致健康监测系统性能下降,形成安全隐患。
使用临近测点值代替故障测点温度信息,就FBG传感器而言,因其串联布设,若数据通道损坏,临近的一组传感器均失效。使用较远传感器监测值代替,存在距离过远,光照影响温差较大,代替不准确等问题,这也是每测点布设温度传感器的原因。实现故障测点的温度信号准确估测,对提高健康监测系统可靠性有着重要意义。
1 传感器布设与数据提取分析
FAST使用FBG温度传感器监测主动反射面结构健康监测系统圈梁格构柱关键应变测点的温度信息。传感器工作原理是外界温度引起光栅周期以及有效折射率发生变化,使反射波长偏移,通过测量中心波长变化量,获取传感器所测温度。
为有效探究远距离布设的温度测点之间的相关性,提取FAST边缘圈梁支承格构柱对应测点的温度信息,每个被监测的格构柱提取一路测点信息,FAST工程圈梁格构柱共50个,有10个格构柱装有测点,被测格构柱编号与测点分布如图1,传感器安装于如图2圈梁支座处靠内侧的水平拉杆中的绿色杆件,测点之间最远距离为500 m。

图1 测点分布示意图

图2 传感器安装位置
监测系统数据采集频率为1 Hz,为降低数据量,滤除高频干扰,避免由于数据长度不统一造成的分析困难,对原始数据进行平均处理,平均时窗为10 min,取每10 min内温度数据平均值作为该时刻温度数据,每测点每日测得144个数据样本。我们提取2019年7月份监测数据,对应记作T1#~T46#,其中31#格构柱测点因采集通道检修关闭,无数据记录,共提取9个测点信息。因环境温度循环周期往往为昼夜,按天对数据进行分组,7月16日数据如图3。
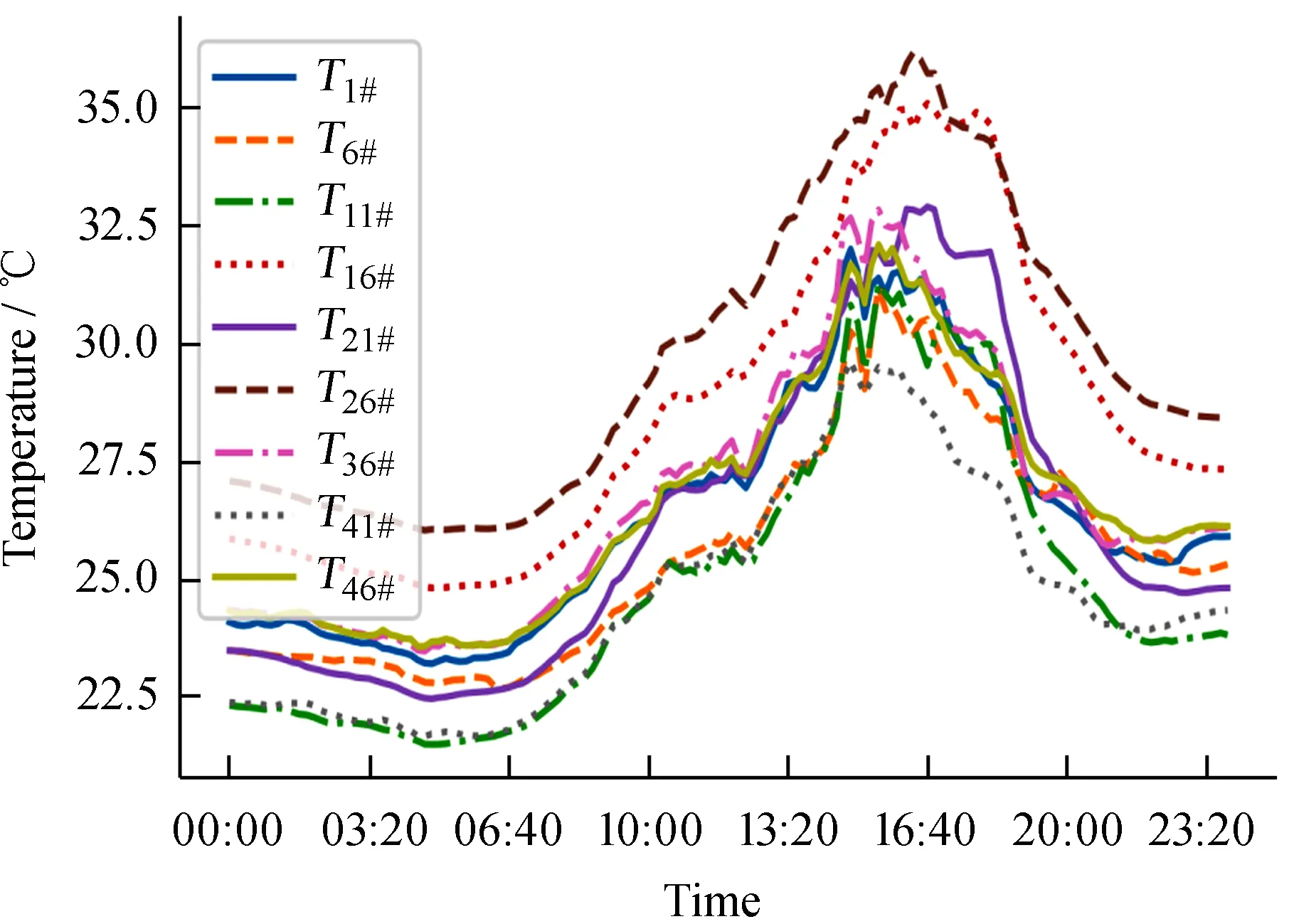
图3 温度监测数据
由图3可以看出,不同测点之间温差较大,最大温差超过5 ℃,波动规律也有一定区别,但其趋势大体一致。两数据样本分别记作X=[x1,x2,...,xn],Y=[y1,y2,...,yn],计算不同样本间线性相关性,相关系数公式为
(1)
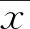

表1 不同测点温度数据相关系数矩阵表
2 线性回归模型
2.1 模型简介
当变量之间高度线性相关时,常用线性回归方法建模。自变量个数为1时,记为x,因变量记作y,一般模型记为
y=β0+β1x+ε,
(2)
其中,β0和β1为模型系数;ε为随机误差。
健康监测温度估测应用中,受光照不均匀的影响,一元回归在某些时刻预测精度较差[8]。引入更多变量,综合不同测点的温度影响,可取得更优的预测结果。当变量个数为多个x1,x2,...,xp时,称为多元线性回归[9],模型记为
y=β0+β1x1+β2x2+...+βpxp+ε,
(3)
其中,β0,β1,...,βp为系数;p为变量个数。当获得n组数据时,模型可简记为矩阵形式
y=XB+E,
(4)
(5)
(6)
其中,Y为因变量向量;X为自变量矩阵;B为各自变量系数向量;E为随机误差向量,随机误差项符合正态分布εi~N(0,σ2),i=1,2,...,n。舍去误差项的影响,最小二乘法求解模型的自变量系数,系数向量估计为
B^=(XTX)-1XTY.
(7)
利用所得自变量估计系数β^0,β^1,...,β^p即可建立经验回归方程
y^=β^0+β^1x1+...+β^pxp,
(8)
其中,x1~xp为自变量输入值;y^为模型输出估测值。
对提取的9个测点数据,取其中一个测点作为因变量即被估测点,其余作为自变量输入,即可通过训练建立多元线性回归模型,当被估测点数据缺失时,可利用自变量输入对信号进行估测。
2.2 最优自变量选取
将1#格构柱测点作为被估测点,其余8个测点温度信息作为候选变量,模型变量的不同分组子集有28~1种。利用16日数据训练模型,将变量按照相关性降序排列逐个增加,划分为8组。
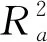
(9)
其中,n=144为样本长度;m=8为全部待选变量个数;p为模型所选变量个数;RSSm为选择全部变量建模的残差平方和;RSSp为模型残差平方和。
(10)
其中,R2为复决定系数即模型拟合度,
(11)
其中,TSS为因变量y=T1#离差平方和,
(12)
(13)
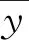
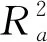

表2 变量分组与模型Cp和数值
3 多重共线性问题与岭回归模型
由表1可知,所有测点两两之间存在极强的相关性,对于多元线性回归模型,因多重共线性模型稳定性出现问题,即模型可能存在一组数k0,k1,...,kp使
k0+k1x1i+...+kpxpi≈0,(i=1,2,...,n) ,
(14)
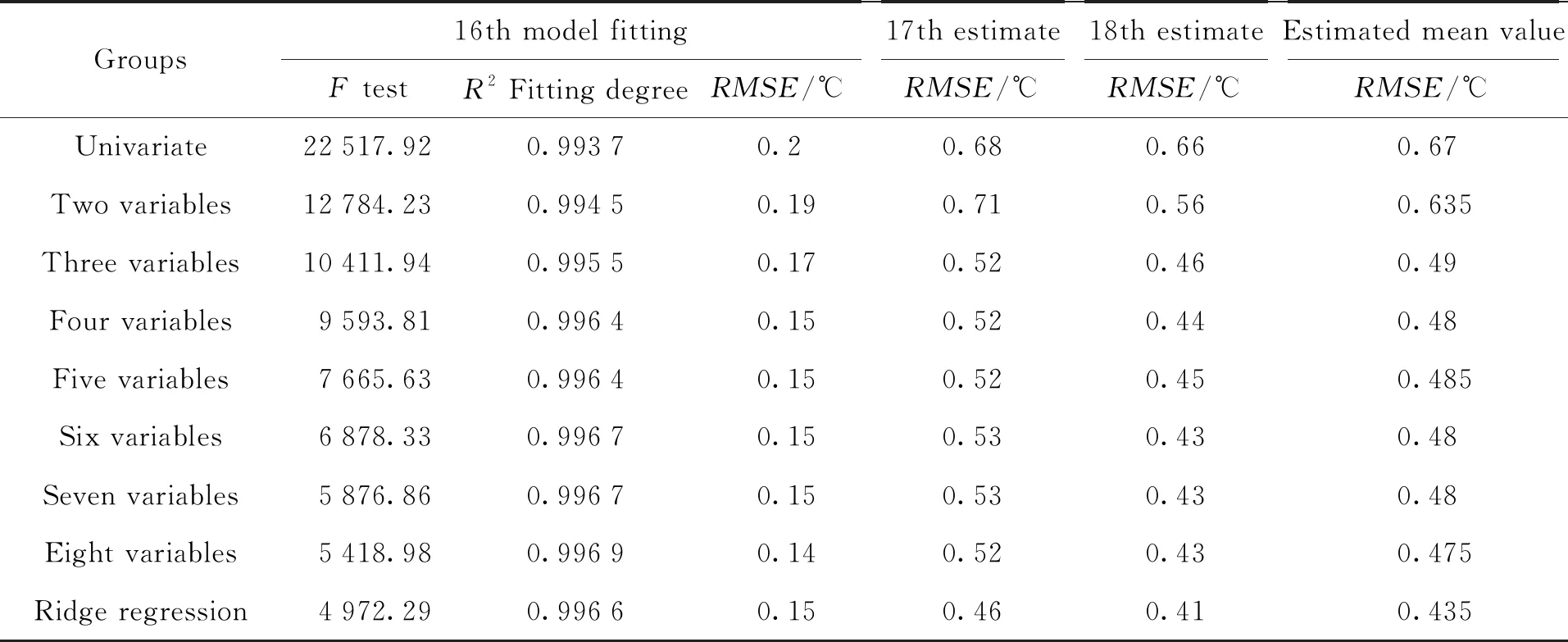
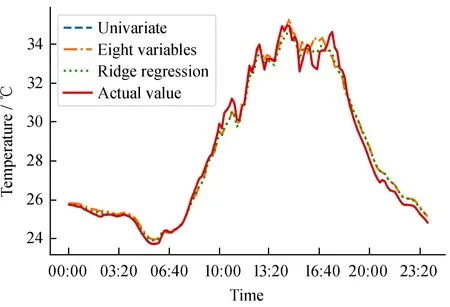
此时设计矩阵秩rank(X) 岭回归法针对多元线性回归模型中的多重共线性问题进行了优化[10],向量系数岭估计定义为 B^(λ)=(XTX+λI)-1XTY, (15) 其中,λ> 0称为岭参数。可见给XTX增加一个正常数矩阵L2范数惩罚项,保证XTX+λI满秩可逆,接近奇异程度比原矩阵减小。XTX+λI随着岭参数增大而增大,模型方差减小,但向量系数估计值B^偏离原值,使模型偏差增大,λ= 0模型退化为普通多元线性回归模型,在应用时,需合理选取岭参数。 应用岭迹法将8个自变量回归系数对应岭迹如图4,按原则选取使所有向量系数稳定的最小的一个岭参数值,确定λ= 6,建立岭回归模型。由图4可见,变量T6#和T26#的系数趋近于0,说明岭回归法训练期间,对自变量有筛选作用。 图4 岭迹图 多元线性回归模型建立后,我们需要判断模型是否可靠。通过F检验确定模型建立的回归方程显著性,统计量公式为 (16) 其中,RSS为模型残差平方和;ESS为回归平方和;n=144为样本长度;p=8为所选变量个数。 (17) 以T1#数据作为被估测点,其他测点数据作为输入变量。使用16日数据训练建立模型,并对17~18日数据进行估测检验,使用均方根误差(Root Mean Square Error, RMSE)评价模型的估测效果,值越小说明模型预测效果越好, (18) 对照前述分组,建立从一元到八元不同类型的线性回归与岭回归模型,并对模型进行估测效果评价,检验及模型估测结果见表3。F检验统计量最低为4 972.29,依旧远大于查表所得Fa(1, 135)=3.911,所有模型通过显著性检验,拟合度均在0.99以上,满足要求。随着融合变量的增加,模型测试的均方根误差随之减小。 表3 模型检验与应用测试结果 一元、八元线性回归、岭回归模型的预测效果如图5,预测曲线与真实值几乎重叠,几种模型均可较好地跟踪估测信号,岭回归法模型精度更高。 图5 真实值与模型预测值对比 本文提取FAST工程主动反射面健康监测系统中跨度500 m范围布设的9个测点温度监测数据,分析可知两两间存在极强的线性相关性,将1#测点作为被估测点,研究了融合其余测点数据对其估测的方法,并对比了不同变量集时模型的估测效果。 多元线性回归与一元回归模型相比,无论是拟合度还是实际估测应用,多元线性回归都具有更好的效果。当输入变量增加至三元时,测试中均方根误差<0.5 ℃。而岭回归与原始多元线性回归相比,模型拟合度略有降低,但可以有效避免变量间的多重共线性问题,对比17日和18日数据的测试,预测精度优于多元线性回归,算法具有更强的抗干扰能力,稳定性好,两日平均均方根误差仅为0.435 ℃。 结果表明,当某测点出现故障时,可使用岭回归法利用近期历史数据训练并建立多元线性回归模型,将正常测点温度信息作为输入,对故障测点输出值进行估测。方法具有较高精度,可用于补充健康监测系统缺失的节点温度信息,在故障测点维修期间保持健康监测系统的正常工作。但该方法使用近期数据进行拟合预测,只能作为测点故障后短期的替补方案。若测点故障过久,可用数据时日相差较大,由于日照天气差别等原因,设备温度场变化规律迁移,估测精度较低,长期数据缺失的估测方法仍需进一步研究。
4 模型检验与评价
4.1 检验与评价指标
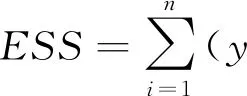
4.2 测试结果
5 总 结
