基于改进SAE 的提升机制动系统故障诊断

李娟莉，闫方元，苗栋，刘怡梦

（1. 太原理工大学 机械与运载工程学院，山西，太原 030024；2. 煤矿综采装备山西省重点实验室，山西，太原 030024）

矿井提升机作为连接井上、井下的关键运输设备，在煤矿安全生产中起重要作用. 制动系统是提升机的重要组成部分，可靠的制动系统是矿井提升机安全运行的必要保障，其潜在故障的存在会引起安全隐患. 开展对提升机制动系统故障诊断方法的研究，对于保障生产人员和设备的安全具有重要意义[1].

在传统故障诊断领域，众多学者针对矿井提升机的故障诊断方法开展了研究. 马立玲等[2]将马氏距离引入到支持向量机算法中，减少了数据中的噪声干扰. 董磊等[3]提出了基于复杂网络聚类算法的提升机故障诊断方法，实现了对故障数据的分类. 以上方法能够实现对提升设备的故障诊断，但是需要大量的先验知识和人工干预，要求建模人员有足够的经验.

近年来，由于传感器技术的大量普及和人工智能技术的兴起，不少学者将深度学习算法应用于故障诊断领域，提高了故障诊断的准确率，数据的利用率更高[4-6]. 自编码器作为一种无监督学习的深度学习算法，在学习特征数据的过程中具有优势. 其中SAE 能降低神经元之间的相互干扰，获取的稀疏特征表达比其他的表达更有效. SUN 等[7]利用SAE 算法学习故障数据的特征表达，引入去噪编码，提高了特征表示的鲁棒性. LU 等[8]在自编码器算法中加入噪声训练，增强了鲁棒性. 赵冬梅等[9]利用批量标准化对自编码器进行优化，优化后的自编码器算法，训练误差更小，特征提取更佳.

为了降低人工干预对故障诊断结果的影响，提升特征挖掘能力，文中提出了一种基于Adam 和Dropout 优化的SAE 神经网络故障诊断方法，采用无监督学习获取特征信息，并将其用于提升机的故障诊断中.

1 故障诊断方法整体框架

使用SAE 进行提升机制动系统故障诊断时，分为四个步骤：数据采集、数据处理、模型训练和模型测试. 故障诊断的整体框架如图1 所示.

图1 故障诊断框架Fig. 1 Fault diagnosis framework

①数据采集. 模型中使用的数据主要来源于提升机正常运行和故障模拟状态下得到的监测数据.通过传感器获得制动系统的监测数据，并导入到数据库.

②数据处理. 对上一步获取到的提升机监测数据进行处理，提取故障特征，创建数据集，并将其划分成训练集及测试集.

③模型训练. 构建SAE 故障诊断模型，并对其进行优化，使用训练集对模型参数进行迭代更新，获得性能优良的诊断模型.

④模型测试. 将测试数据集应用在训练好的诊断模型中，验证模型的有效性.

2 故障机理分析

以实验室的2JTP-1.2 型提升机为例，该提升机采用盘式制动器进行制动，由碟形弹簧产生制动力，当制动油压下降时，蝶形弹簧的压力不断减小，此时弹簧推动活塞，使闸瓦接近制动盘，产生制动力矩，提升机处于制动的过程. 反之，液压油推动碟形弹簧，使闸瓦逐渐离开制动盘，提升机处于松闸的过程.

由于提升机结构复杂加上工作环境的强振动、重负荷，制动系统失效产生的原因较多，常见的故障现象及原因分析如图2 所示.

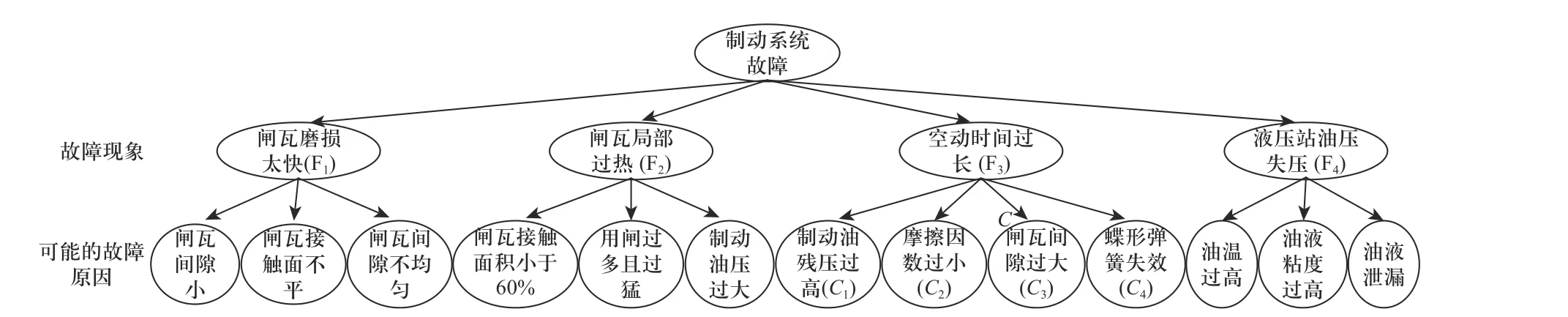
图2 制动系统主要故障及原因Fig. 2 Main faults and causes of the brake system

闸瓦磨损太快：闸瓦性能的优劣影响着制动力矩的大小，在制动器受力不均时，导致各闸瓦的接触面积变小，闸瓦磨损加快，会造成刹车失灵，引发故障. 闸瓦间隙小、闸瓦接触面不平、闸瓦间隙不均匀等因素可以加快闸瓦磨损.

闸瓦局部过热：闸瓦的温度过高，会烧毁制动盘，制动器不能产生制动力矩，造成制动失效. 闸瓦接触面积小于60%、用闸过多且过猛、制动油压过大等因素可以造成闸瓦局部过热.

空动时间过长：提升机的空动时间过长（空动时间指的是保护回路断电时，闸瓦接触到制动盘所用的时间，根据《煤矿安全规程》的规定，盘式制动闸的空动时间不得超过0.3 s），会使作用在制动盘的制动力减小，导致无法及时制动，造成过卷和跑车事故.制动油残压过高、摩擦因数过小、闸瓦间隙过大、蝶形弹簧失效等因素可以导致空动时间过长.

液压站油压失压：是指液压系统不产生压力或者产生的压力不能达到最大油压，可能导致提升机松不开闸，甚至导致闸瓦失效. 油温过高、油液粘度过高、油液泄漏等因素可能导致液压站油压失压.

由上述分析可知，影响制动系统运行状态的参数主要包括闸瓦间隙、制动油压、空动时间、液压站残压等，分析这些参数能够对常见的故障现象进行诊断. 提升机在运行过程中，产生的监测数据具有数据量大、数据冗余或缺失等特点，深度神经网络算法在分析数据规律、弥补缺失数据方面，具有较好的效果. 文中采用深度神经网络算法，对提升机的监测数据进行处理和分析.

3 深度神经网络算法

无监督特征学习是从无标签数据中提取数据的特征表达，尤其在标签数据较少的情况下，具有很大的优势[10]. SAE 作为一种典型的无监督特征学习算法，在诊断模型中能够获取反映提升机运行状态的特征.

3.1 稀疏自编码器

自编码器的基础结构包括3 层，如图3 所示. 其第1 层为输入层，用于接收输入数据；第2 层为编码层，也称为隐藏层，用于提取数据中的特征信息，提取的特征也称为编码，编码的维度取决于编码层的节点数；第3 层为输出层，就是通过解码过程重构为原始输入数据，使得重构误差最小.

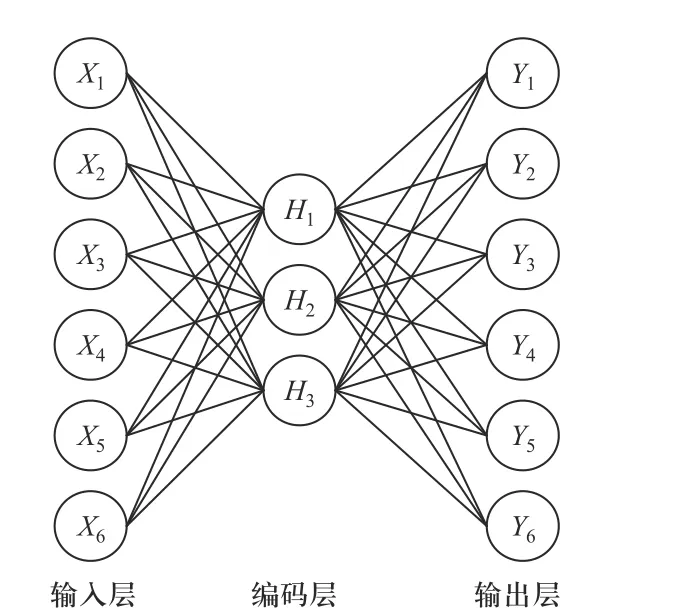
图3 自编码器结构图Fig. 3 Auto encoder structure

对于给定的数据X=（x1,x2,···,xm) （ 其中m为样本的个数），假设f为编码函数，则编码层的数据表示为

在整个训练过程中，循环迭代更新权重和偏差，使成本函数的数值尽可能小.

3.2 Dropout 正则化

Dropout 方法常用于在网络模型的训练过程中减少过拟合现象[11]. 按照一定概率控制神经元的激活量，降低神经元之间的相互干扰，使提取的特征表达更具代表性. 在文中的神经网络训练中，将采用Dropout 方法减少过拟合和提高特征提取能力.

算法的实际体现过程为：①初始设定一个范围在(0,1]中的数X；②在每次训练迭代中，将隐藏神经元的输出随机分配一个范围在[0,1]的数Y；③如果某个神经元的Y小于等于X，那么此神经元的输出保存，否则将此神经元的输出设为0，不参与循环迭代.

3.3 Adam 算法

Adam 算法是将RMS-Prop 算法和L2 范数相结合，对随机梯度下降方法进行改进和优化的一种算法[12]. 该算法的优点是计算速度快、内存使用较少、能较好地处理稀疏梯度的问题.

对于不同数据的收敛要求，需要有不同的学习率. 学习率的选取是Adam 算法根据矩估计的不同数值，进行自行选择. 算法的实现过程为：①设置初始的学习率、矩估计的指数衰减速率；②建立目标函数的梯度，计算其对应的偏矩估计；③修正矩估计的偏差，计算出更新量，进入下一步的迭代.

3.4 基于SAE 的故障诊断模型

在文中3.1 节经典自编码器模型的基础上，结合Dropout 和Adam 算法，建立了基于SAE 的故障诊断模型. 模型的训练、测试过程如图4 所示，具体的诊断过程如下.

图4 诊断流程图Fig. 4 The flowchart of the diagnosis method

（1）使用无标签的训练数据集，初始化诊断模型的参数.

①初始化设置稀疏常数、学习率、Dropout 比例等参数，调整权重和偏差，使诊断模型有较好的分类效果.

②计算隐藏层节点的平均激活量，使其接近稀疏常数；加入稀疏项后，计算每个输出层的成本函数，迭代更新权重和偏差，使成本函数的数值尽可能小.

（2）使用有标签的训练数据集，训练诊断模型，进行故障分类，获取诊断规则.

①使用步骤（1）中获取的权重和偏差等参数，初始化故障诊断模型；设置训练数据集大小、Dropout 和迭代次数等参数，进行故障模型训练.

②计算输出层的成本函数，迭代微调权重和偏差，获得提升机的诊断规则.

（3）使用有标签的测试集，测试诊断模型的分类性能. 对比分类结果与标签输出结果，统计不同故障类型的故障诊断准确率.

上述的诊断模型发挥了SAE 网络无监督学习数据特征的能力，将提取的特征表达应用在故障分类中，在此基础上加入Dropout 正则化方法，使SAE 提取更有效的特征表达. 另外，对于故障数据稀疏的特点，基于动量的思想，采用Adam 算法对诊断模型进行迭代训练，减少了数据稀疏梯度对诊断结果的影响，缩短了训练时间.

4 试验验证

4.1 验证过程

为了验证文中提出的基于SAE 的神经网络方法对提升机故障诊断的效果，以实验室2JTP-1.2 型提升机为研究对象，利用提升机故障试验平台采集正常状态和多种故障下的数据进行分析.

试验中，通过故障模拟，采集故障数据，故障模拟方法见课题组发表的论文[13]. 将试验台采集的数据，进行冗余、缺失及标准化等预处理后，获得样本数据集. 标准化数据处理的过程为：汇总同一种故障类型的数据，分别统计出其在95%置信度下的数据区间范围，并以此作为数据离散化处理的依据，根据不同的区间范围，把数据分成不同的类别，用数字0、1、2 表示. 随机选取每类样本数据中的1/2 作为训练数据集，剩下的1/2 作为测试数据集，每一组数据都包含有4 个数据采样点. 试验平台如图5 所示.部分样本数据集如表1所示.

图5 试验平台Fig. 5 Test platform

表1 中V1为闸瓦间隙；V2为制动油压；V3为液压站残压；V4为接触面积百分比. 表中故障类型的符号含义详见图2，F0为正常运行状态下的数据.

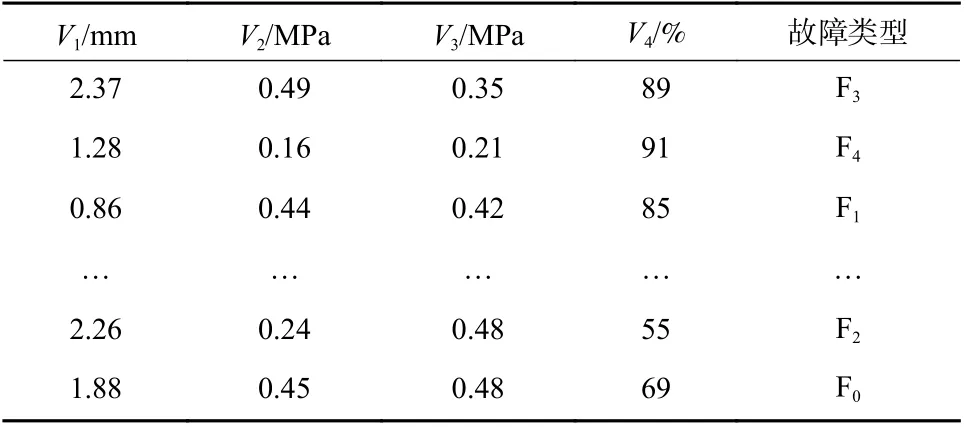
表1 神经网络的检验样本示例Tab. 1 Sample examples of neural network

4.2 诊断正确性分析

利用上文第3 节的算法，针对空动时间过长的故障现象，计算出可能的故障原因可信度数值如图6所示.

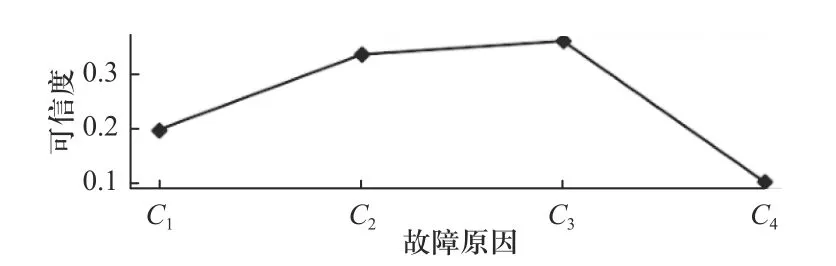
图6 故障现象与故障原因匹配的可信度Fig. 6 The reliability of the matching of the failure phenomenon and the failure cause

在图6 中，故障原因的符号含义详见图2.C1的可信度为0.199，C2的可信度为0.336，C3的可信度为0.361，C4的可信度为0.103. 从图6 中可以看出，闸瓦间隙过大引起空动时间过长的可能性大，下面对诊断结果进行验证.

在提升机的制动过程中，出现空动时间过长的故障现象，由第2 节可以知道，导致空动时间过长的主要因素包括制动油残压过高、摩擦因数过小、闸瓦间隙过大和蝶形弹簧失效等. 在试验之前，对每个闸的蝶形弹簧刚度和预压缩量进行了测量，都使其达到标准要求，故排除了蝶形弹簧失效的因素；在实际运行中，摩擦因数在正常范围内，故排除了摩擦因数过小的因素；绘制制动油压的曲线图如图7 所示，该图可以说明制动油残压值小于0.5 MPa，在正常范围内，故排除了制动油残压过高的因素；根据闸瓦位移的数据，绘制出闸瓦位移曲线如图8 所示，从图8中可以看出，闸瓦间隙超限，由此判断出该故障可能由闸瓦间隙过大引起，需要调整闸瓦间隙.

图7 制动油压曲线Fig. 7 Brake oil pressure curve

图8 闸瓦位移曲线Fig. 8 Brake shoe displacement curve

4.3 结果分析

在前期的算法理论研究中，探究了不同比例的Dropout 对SAE 神经网络分类效果的影响，发现当Dropout 的比例为30%时，诊断模型能实现较好的分类效果，因此在诊断模型的试验过程中将Dropout 方法的比例设置为30%.

为了测试不同数量的样本数据对神经网络分类效果的影响，选取故障类型为F1的样本数据，得到的试验结果如图9 所示. 从测试结果可以看出，在训练数据量少的情况下，随着样本数据增加，诊断模型准确率的提升效果更明显，可以说明Dropout 方法在算法中可以有效地减少过拟合的现象；当样本数据量较多时，诊断模型的准确率保持在93%以上.在SAE 中，由于Dropout 正则化方法对深度神经网络的实现效果有一定的影响，为了检验优化后的SAE 诊断模型在矿井提升机故障诊断中的优势，本部分采用改进前的SAE 作对照组，用相同样本对两种不同的神经网络进行对比试验. 避免单次试验的偶然性，重复进行10 次试验，统计模型诊断的准确率.上述试验中发现，样本数据量的大小影响了模型诊断的效果，将处理过后的各类故障数据分别抽取600 组数据，进行诊断模型的分类测试，对两种诊断模型均采用相同的测试集，测试结果如表2 所示.表中用SAE-D 表示上文所提的神经网络，用SAE 表示未添加Dropout 的神经网络. 经比较其准确率可发现，添加了Dropout 正则化的SAE 深度神经网络，对于大多数故障，其平均分类精度达到94%，具有较好的分类效果.

图9 不同样本数量的神经网络准确率Fig. 9 Accuracy of neural network with different sample sizes

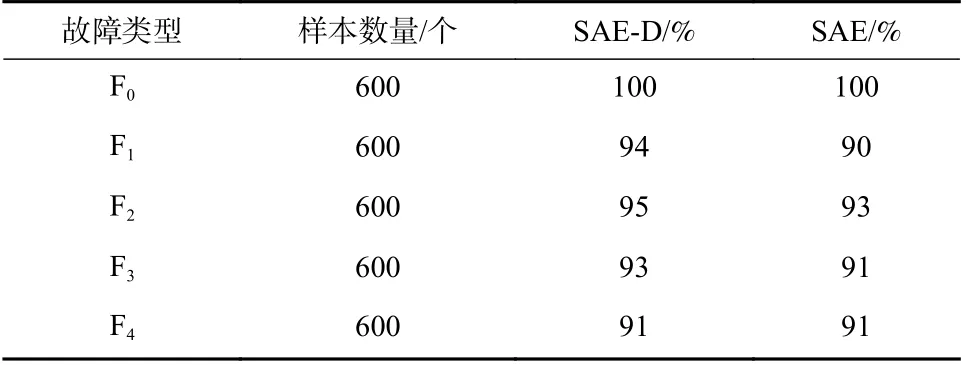
表2 故障诊断测试准确率Tab. 2 Test accuracy of fault diagnosis

可见，与未添加Dropout 正则化的SAE 深度神经网络相比，加入Dropout 正则化的SAE 深度神经网络，可以提高提升机制动系统的故障诊断准确率，能更有效地提升深度神经网络的分类性能.

5 结 论

融合了Dropout 正则化和Adam 算法的SAE 模型，可以无监督学习故障特征，进而有效地进行提升机故障诊断. SAE 模型能有效地获取数据特征信息，不需要标注大量的标签数据，在特征提取方面有一定优势；优化后的SAE 诊断模型，平均准确率能够达到94%，能有效地进行提升机的故障诊断；诊断模型加入Dropout 正则化方法后，减少了过拟合现象和神经元之间的相互影响，对训练模型的神经元控制有着较好的自由度. 同时Adam 算法改善了模型的训练过程，减少稀疏数据中局部最优点对模型训练的影响.