楔面角度扰动对斜爆轰结构的影响研究

刘曦，李健

（北京理工大学 爆炸科学与技术重点实验室，北京 100081）

驻定斜爆轰波发动机[1]拥有结构简单、反应高效等优点，是最有可能用于下一代高速飞行器的动力系统之一. 驻定斜爆轰发动机研究的关键是斜爆轰现象. 目前国内外已有很多学者对斜爆轰的波系结构、波面结构、驻定条件等问题进行了深入研究.国内外经典的研究[2-5]表明，斜爆轰波有两种典型的结构：突跃过渡结构和平滑过渡结构. 其中，突跃过渡斜爆轰的流场存在三波点、反射波和滑移线等复杂波系结构，平滑过渡斜爆轰的波系结构相对简单，仅有一条滑移线. YANG 等[6]针对突跃过渡斜爆轰的过渡区进行了细致的研究，共发现3 种过渡区结构：分别为Type IV、Type V 和Type VI 结构， 这些结构是根据EDNEY[7]提出的归类方法命名的. 虽然已有很多学者对斜爆轰进行了研究，但这些研究大多假设楔面和来流方向夹角为固定值，这显然是一种理想假设. 在飞行器飞行中，很难使来流始终保持同一方向，此时楔面和气流的夹角就会发生扰动.ZHANG 等[8]忽略楔面角度的转动过程，令楔面瞬间达到不同的角度，研究了瞬间角度变化对流场造成的影响，这无疑是很有意义的，不过由于忽略楔面角度变化的过程，与实际情况有所差距.

为更真实地探究楔面角度扰动对斜爆轰的影响，利用LevelSet 水平集函数[9]描述楔面，并将时间引入LevelSet 水平集函数，实现了楔面角度随时间的连续变化. 考虑两种楔面角度扰动情况，分别为：楔面角度先增大后减小、楔面角度先减小后增大. 同时，由于斜爆轰有两种典型的结构：突跃过渡结构和平滑过渡结构，所以本文中依次选取稳态的突跃过渡斜爆轰和平滑过渡斜爆轰作为初始状态，然后分别考虑两种角度扰动对流场的影响.

1 控制方程及来流参数设置

控制方程采用二维无黏带化学反应的多组分可压缩Euler 方程组，具体形式如下：

式中：p为压力；ρ 为密度；u，v分别为x和y方向的速度；E为总能量；Q为反应热；yB和yC分别为诱导和反应阶段的进度变量；R～为通用气体常数.

化学反应模型采用NG 等[10]数值实验中使用的两步法模型，来流气体的初始参数如表1 所列.

表1 来流气体的初始参数Tab. 1 The initial parameters of inflow gas

2 数值计算方法和收敛性验证

2.1 数值计算方法

采用欧拉网格计算，计算域长0.1 m，高0.15 m.在流场中设置一楔面，超音速可燃预混气体撞击楔面形成斜爆轰波. 流场左侧为来流边界，上侧和右侧为出流边界，楔面表面使用无滑移边界条件. 控制方程用有限体积法数值求解，空间离散采用3 阶精度MUSCL 格式，时间离散采用3 阶精度龙格库塔方法.依次取突跃过渡斜爆轰和平滑过渡斜爆轰作为计算的初始状态，楔面角度以固定的角速度分别先增加后减小、先减小后增加，以探究楔面角度扰动对流场的影响. 楔面角速度假设为常数，在实际发动机中楔面转速可达到6×105(°)/s[8]，本文中取为105(°)/s，初始楔 角均为23°，来流速度V∞取1 800 m/s 和2 300 m/s，分别对应突跃过渡斜爆轰和平滑过渡斜爆轰. 角度扰动的范围为±10°，即两种扰动分别为23°→33°→23°和23°→13°→23°.

2.2 网格收敛性测试

网格精度可以用爆轰诱导区ΔI内网格点的数量来衡量. 根据来流气体参数可以计算出CJ 爆轰的诱导区长度ΔI，分别在诱导区ΔI内采用10、20、40 个网格，对来流速度V∞=1 800 m/s、楔面角度θ=23°时的稳态斜爆轰问题进行计算，得到的结果如图1 所示.

由 图1 可 以 看 出，10 pts/ΔI精 度 的 计 算 结 果 和20 pts/ΔI精度的计算结果相比，波阵面上捕捉到的三波点数量较少，流场中波系结构也较模糊，而20 pts/ΔI精度的计算结果和40 pts/ΔI精度的计算结果相比，均能清晰捕捉到斜爆轰波的各种波结构，流场几乎看不出区别. 以波阵面三波点间距l来定量分析3 个 结 果，在10 pts/ΔI精 度 下l平 均 为4.23 mm，20 pts/ΔI精 度 下l平 均 为2.74 mm，40 pts/ΔI精 度 下l平均为2.69 mm，后两者结果相近，因此认为网格精度为20 pts/ΔI时能够满足计算精度.

图1 网格收敛性测试(V∞=1 800 m/s，θ=23°，t=0.3 ms)Fig. 1 Verification of grid resolution convergence(V∞=1 800 m/s，θ=23°，t=0.3 ms)

3 数值结果和讨论

3.1 突跃过渡斜爆轰对23°→33°→23°角度扰动的响应

扰动开始，楔面首先上升. 楔角增大，压缩效应增强，斜激波后温度、压力上升，气体经诱导区吸收活化能所需距离缩短，诱导区变短，从图2(a)和2(b)可以看到，诱导结束产生的爆燃波明显前移，图3(a)中斜激波间断后诱导区变短. 突跃过渡斜爆轰中，斜激波与斜爆轰波相交，形成三波点和横波，横波与楔面交点处出现温度和压力间断，如图3(a)和3(b)中曲线0.04 m 处的峰值. 楔面上升过程中，由图2(a)和2(b)可以看到，斜激波和斜爆轰波角度差减小，横波减弱，与楔面交点处压力峰值减小，如图3 所示. 当横波消失时，斜激波平滑过渡为斜爆轰波，即成为平滑过渡斜爆轰，如图2(c)所示. 楔角继续增大，斜爆轰波最终发展成脱体斜爆轰.

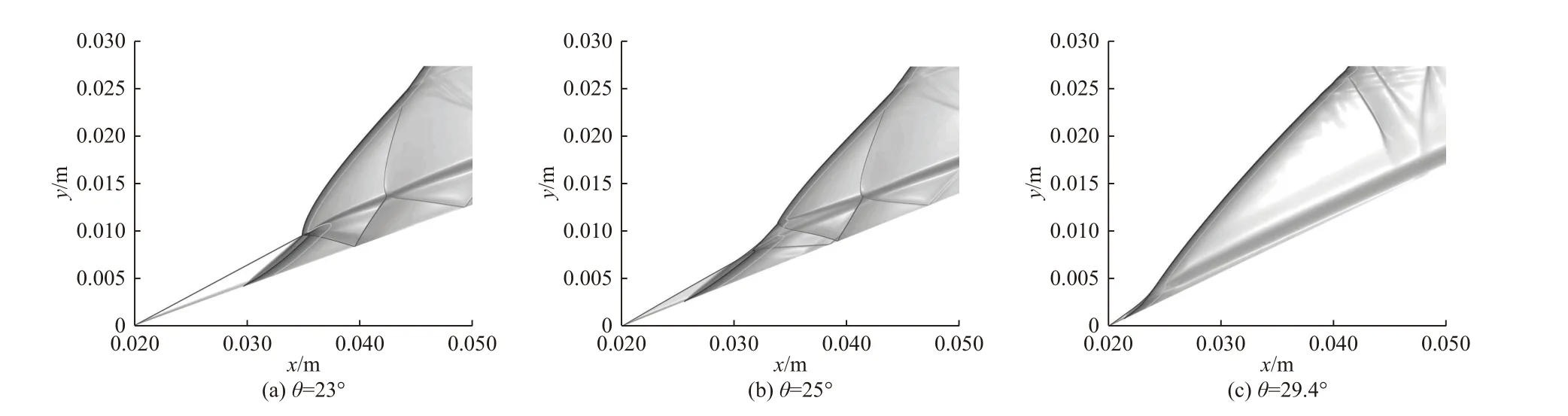
图2 楔面上升阶段流场的变化过程Fig. 2 The changing process of flow field when the wedge is rising

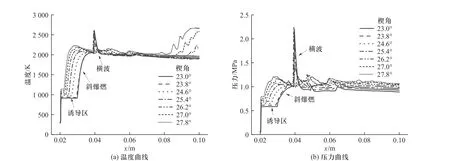
图3 楔面上升阶段表面的温度、压力曲线Fig. 3 Temperature and pressure curve of wedge surface when the wedge is rising

楔角达到最大后开始减小. 在楔面下降阶段的0.1 ms 内，斜爆轰波响应速度很慢，整体流场几乎没有变化，流场的演变主要发生在楔角恢复至23°之后，图4 给出了不同时刻的流场图像. 流场中首先得到双马赫反射结构，如图4(a)所示，马赫杆由横波与楔面作用得到. 马赫杆后温度、压力很高，虽然气体在马赫杆前尚未活化，但经马赫杆压缩后，立即开始反应，形成反应马赫杆. 此外，在楔面发现了压力和温度的衰减振荡现象，如图5 所示. BENDOR 等[11-12]曾对这种现象进行研究，认为这是由于振荡流管周围流动是亚音速，而内部是超音速造成的. 斜爆轰波受楔面支持不足，波角持续减小，向下游移动，这使横波和马赫杆也后移. 当马赫杆移至某一位置时，马赫杆前气体经斜激波压缩能自点火，在马赫杆前出现斜爆燃波，如图4(b)所示. 由于斜爆燃波的压缩作用，其前出现一簇斜激波，这一簇激波和爆燃波共同对横波和马赫杆作用，使横波和马赫杆弯曲、连接在一起，如图4(c)所示. 一段时间后，斜爆轰波倾角和位置逐渐稳定，横波的强度和角度也随之稳定，与楔面的反射由马赫反射演变成规则反射，流场恢复为最初的突跃过渡形态.

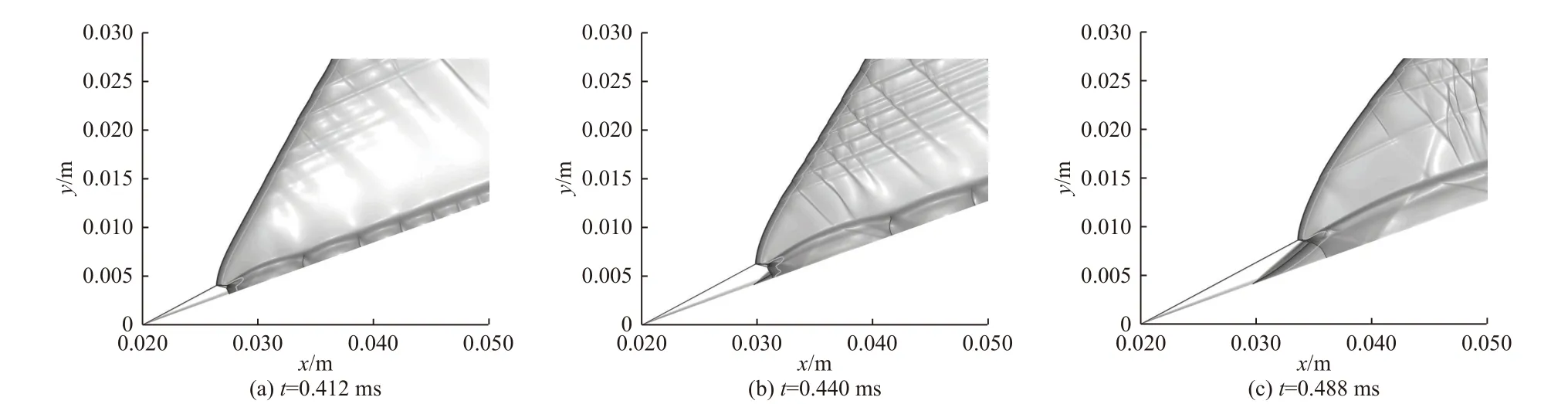
图4 楔角恢复23°后流场的变化过程Fig. 4 The changing process of flow field after the wedge angle reaches 23°

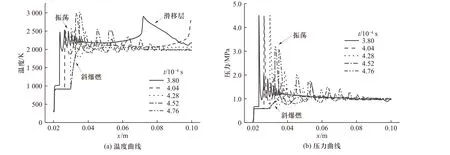
图5 斜爆轰波向下游移动时楔面的温度、压力曲线Fig. 5 Temperature and pressure curve of wedge surface when the ODW is moving downstream

3.2 突跃过渡斜爆轰对23°→13°→23°角度扰动的响应

扰动开始，楔角首先减小. 斜激波减弱，诱导区变长，斜爆燃波向下游移动，如图6(a)和6(b)所示.斜爆燃波与横波相交，首先发生Type I 型相互作用，如图6(a)所示. 斜爆燃波继续向下游移动，相交类型由Type I 型变成Type II 型，如图6(b)所示. Type II 型结构中的马赫杆诱发气体反应，成为反应马赫杆，它强于爆燃波，不断伸长最终使爆燃波消失. 反应马赫杆与楔面交点处温度和压力急剧增加，如图7 所示.楔面继续下降，斜爆轰波缺少楔面支持，最终移出计算域，计算域中只剩下斜激波.

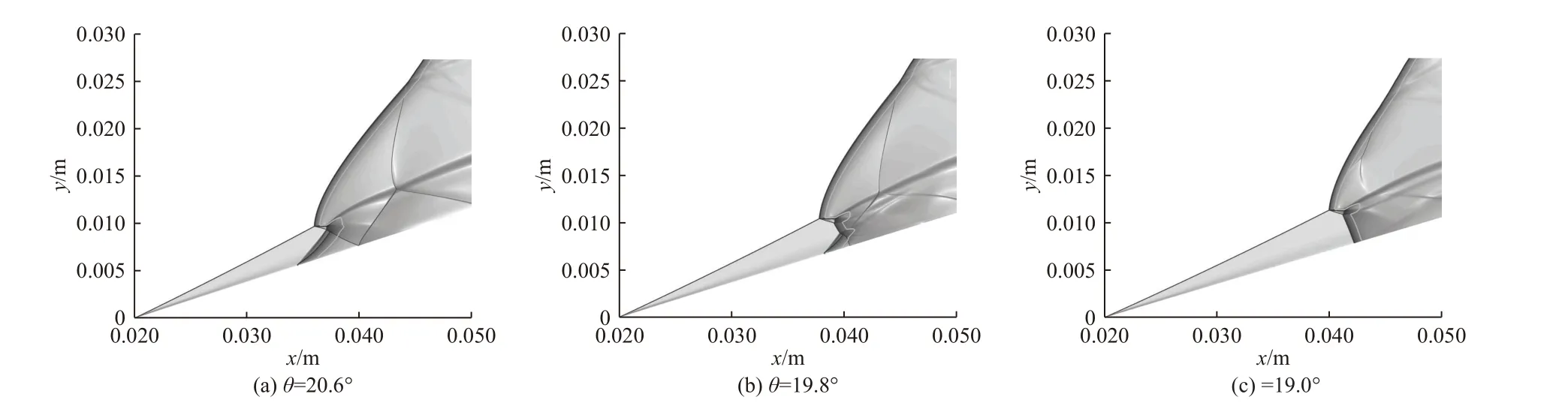
图6 楔面下降阶段流场的变化过程Fig. 6 The changing process of flow field when the wedge is falling

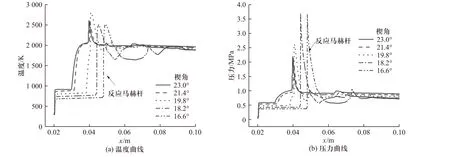
图7 楔面下降阶段表面的温度、压力曲线Fig. 7 Temperature and pressure curve of wedge surface when the wedge is falling

楔面上升阶段，斜激波变强，本例中，楔角升至23°后，斜激波后出现新的爆轰波，爆轰波追赶、相交于斜激波，相交部分成为新的斜爆轰波，如图8(a)和8(b)所示. 出现爆轰波时，楔面已恢复到23°，此时，斜激波已匹配新的楔面角度（23°），而斜爆轰波发展需要时间，斜激波和斜爆轰波角度差的增大需要过程. 角度差较小时，产生的横波很弱，与楔面相交处温度、压力升高较小，随着斜爆轰波角度增加，横波增强，使楔面上交点处的温度、压力大幅增加，如图9所示.

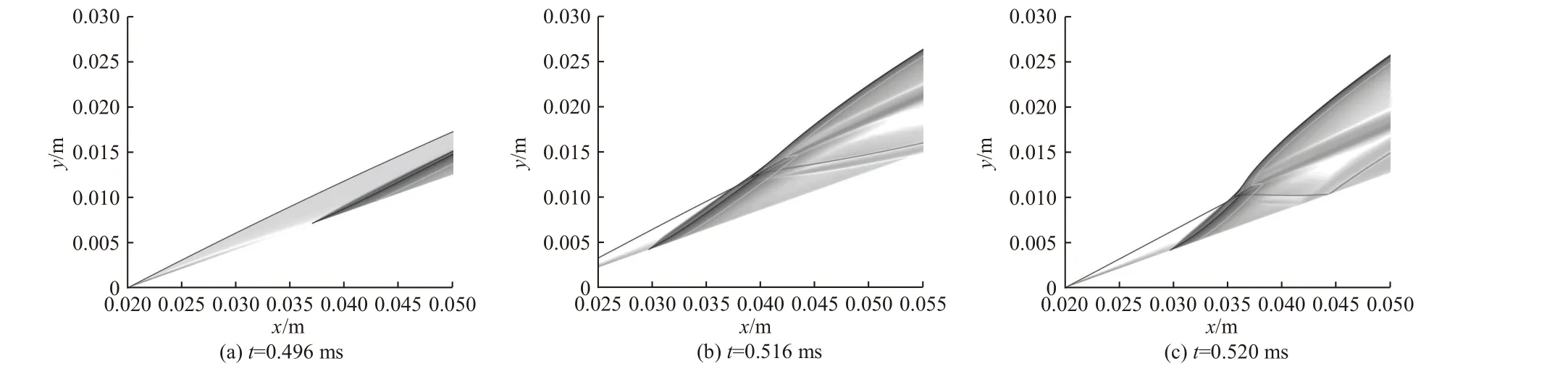
图8 楔角恢复23°后流场的变化过程Fig. 8 The changing process of flow field after the wedge angle reaches 23°

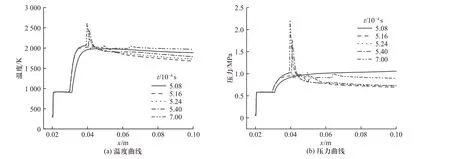
图9 楔角恢复23°后楔面的温度、压力曲线Fig. 9 Temperature and pressure curve of wedge surface after the wedge angle reaches 23°

3.3 平滑过渡斜爆轰对23°→33°→23°角度扰动的响应

平滑过渡斜爆轰波从斜激波到斜爆轰波的过渡是平滑的，不会出现三波点和横波结构，流场较为简单. 扰动开始，楔面上升，原本就很短的诱导区进一步缩短，楔面表面温度和压力升高.

楔面下降时，离楔面更近的波面先受影响，角度减小，下游距楔面较远的波面倾角更晚开始减小，波面上下游之间形成角度差，产生横波，如图10 所示.楔面不断下降，波面角度差变大，横波逐渐增强. 与楔面交点处温度和压力增加，如图11 所示.

图10 楔面下降阶段流场的变化过程Fig. 10 The changing process of flow field when the wedge is falling

图11 楔面下降阶段表面的温度、压力曲线Fig. 11 Temperature and pressure curve of wedge surface when the wedge is falling

3.4 平滑过渡斜爆轰对23°→13°→23°角度扰动的响应

扰动开始，楔角减小，斜激波变弱，诱导区变长，斜爆燃波向下游移动. 斜激波与斜爆轰波角度差增加，产生横波，演变成突跃过渡斜爆轰，如图12(b)所示. 楔角继续减小，爆燃波后移，先后以Type I 和Type II 形式与横波相交，如图12(c)、12(d)所示，形成反应马赫杆. 反应马赫杆逐渐伸长，与楔面相交，交点处温度和压力增加，如图13 所示. 由于楔面支持不足，斜爆轰后移，最终计算域中仅剩一道斜激波.

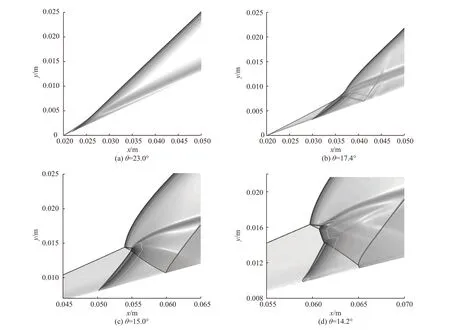
图12 楔面下降阶段流场的变化过程Fig. 12 The changing process of flow field when the wedge is falling

图13 楔面下降阶段表面的温度、压力曲线Fig. 13 Temperature and pressure curve of wedge surface when the wedge is falling

图14 所示为楔面上升阶段流场的变化过程，图15 所示为此阶段的温度及压力变化曲线. 在此阶段，斜激波增强，重新出现爆轰波，爆轰波追赶、相交于斜激波，向后反射一道稀疏波，如图15 中箭头所示. 斜激波与爆轰波相交部分形成斜爆轰波并生成横波，由于二者角度差不明显，横波很弱， 楔面继续上升，斜激波角度增加，且增加速度快于斜爆轰，二者角度差减小，横波变弱逐渐消失，流场重新恢复为平滑过渡斜爆轰.

图14 楔面上升阶段流场的变化过程Fig. 14 The changing process of flow field when the wedge is rising

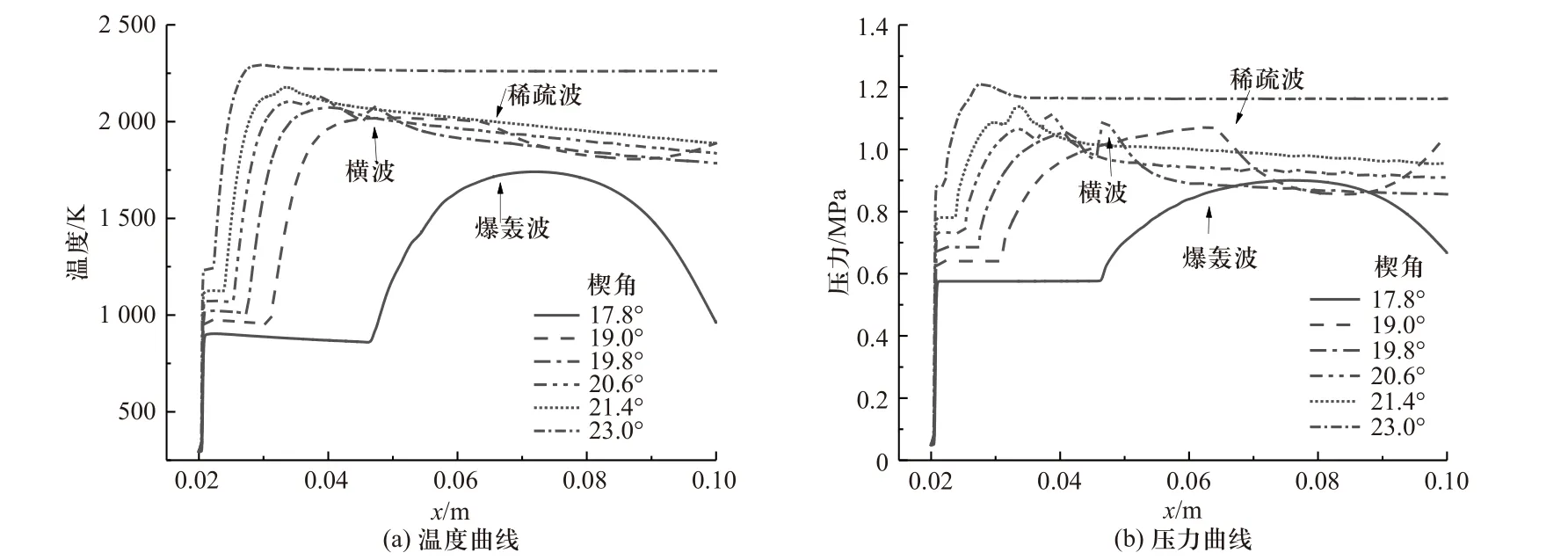
图15 楔面上升阶段表面的温度、压力曲线Fig. 15 Temperature and pressure curve of wedge surface when the wedge is rising

3.5 楔面运动时斜激波和斜爆轰波角度差的变化

在上述4 种情况中可以看出，斜激波和斜爆轰波的角度差对流场结构演变起关键作用. 由于斜激波距楔面更近，且其后没有化学反应，不需要时间使化学反应达到新的平衡，因此能更迅速地改变倾角以匹配楔面的运动. 斜激波和斜爆轰波倾角变化快慢不同，二者角度差将出现变化. 为说明这种变化，以3.1 节的结果为例，与楔角固定的稳态斜爆轰进行对比，图16 为楔角取25°和27°时的稳态斜爆轰以及楔面上升和下降时的运动斜爆轰图像.

图16 稳态斜爆轰波和运动态斜爆轰波的对比Fig. 16 A comparison of steady oblique detonation and moving oblique detonation

针对图16，表2 列出了每一幅图中斜激波和斜爆轰波的倾角，并计算角度差. 可以看到，无论楔面静止还是运动，在相同楔角下的斜激波倾角差别很小，而斜爆轰波对楔面运动的响应总是有所滞后. 当楔面上升时，斜爆轰波倾角小于稳态时的倾角，当楔面下降时，斜爆轰波的倾角大于稳态时的倾角. 这种迟滞性导致楔面上升时波面角度差减小，横波减弱，突跃斜爆轰向平滑斜爆轰转变；楔面下降时，波面角度差增大，使横波提前出现，形成双马赫反射结构.

表2 不同条件下斜激波和斜爆轰波的倾角以及角度差Tab. 2 The angle and angle difference of oblique shock and oblique detonation under different situation

4 结 论

通过对斜爆轰波受楔面角度扰动问题的数值模拟，分别研究了两种角度扰动对两种典型结构斜爆轰波的影响. 楔面角度增加时，两种结构的诱导区长度均变短，斜激波、斜爆轰波倾角均会增加. 其中突跃过渡斜爆轰受楔角增加影响时，会逐渐转变成平滑过渡斜爆轰； 楔面角度减小时，两种结构的诱导区长度均变长，斜激波、斜爆轰波倾角均会减小，其中，突跃过渡斜爆轰中，斜爆燃波向下游移动与横波依次发生Type I 和Type II 型相互作用，Type II 型结构中的马赫杆逐渐伸长，斜爆燃波消失；平滑过渡斜爆轰受楔角减小影响时，首先转变成突跃过渡斜爆轰，之后过程与突跃过渡斜爆轰受楔角减小的影响相类似. 脱体斜爆轰受楔角减小影响时，先出现类似双马赫反射结构，并在楔表面产生温度和压力振荡. 楔角的减小会使斜爆轰后移，移出计算域后，只留下一道斜激波，此后楔角增加，某一时刻会在激波后形成爆轰波，爆轰波追赶上激波，重新形成斜爆轰波.

楔面角度的扰动可以模拟来流方向的扰动，也能模拟通过改变楔角对斜爆轰进行控制的过程，数值结果对工程设计有指导意义. 楔角增加，楔表面的温度和压力增大，设计发动机楔形结构时必须满足一定强度和耐高温性. 楔角减小，斜爆轰波可能移出发动机，导致熄火，实际设计时要考虑如何避免熄火. 楔角变化，会产生各种波与楔面相交，交点处的温度和压力极高，楔表面还可能出现温度和压力振荡，设计时必须考虑这些因素对结构的破坏，给予足够的强度冗余.