基于超声短时傅里叶变换的液压管路内油液压力测量方法研究

侯怀书，张毅

(1.上海应用技术大学机械工程学院，上海201418;2.上海物理气相沉积(PVD)超硬涂层及装备工程技术研究中心，上海201418)

0 前言

在现代工业与国防中，液压传动有着非常广泛的应用。辅助部分是液压传动系统5个主要部分之一，其中油管与压力表又是辅助部分中的主要元件，分别承担着输油与压力测量的任务。目前，国内外使用的压力表大多为介入式的，常用应变式、压阻式、振弦式等机械压力表，其最大的缺点是要在管路的特定位置开孔引压测量，在10～30 MPa压力的工作环境下极易导致开孔边缘局部应力集中，容易留下安全隐患。因此，液压系统输油管路压力非介入式测量方法是一种具有广阔发展前景的技术。

周正义等指出：国内外非介入式压力测量方式并不成熟，尚处于探索阶段，应用在液压系统的非介入式压力测量方法主要有应变法和超声波法。其中，应变法要在管路外壁贴应变片，压力变化引起应变片应力变化来检测压力变化，这种方法安装要求高，应变片粘贴工艺复杂，并且应变片本身容易受温度影响，不宜长期使用。常旭等人提出一种利用超声表面波方式测量管路内液体压力的方法，其原理是管内油液压力会引起管壁弹性模量等物理量发生改变，超声波在管壁中的传播速度也会发生相应变化。这种方法有一定的可行性，但是是通过管壁物理量变化间接反映内部油液的压力，而油液本身相关的物理量无法测量，并且此方法只适用于管壁较薄、压力能引起管壁发生形变的情况。杜寅飞等指出：油液受到压力时，其密度、体积弹性模量等物理性质都会发生一定的变化，因此应采集在油液中传播的超声信号，获取更多直接反映油液相关物理量变化的信息。樊文跃指出：超声波法压力检测方法主要有两种，一种是基于声速的测量方法，另一种是基于幅值衰减的测量方法。目前，超声波测压方法主要是基于声速的，同时使用声速和衰减来测量管路中油液压力的方法未见报道。

本文作者阐述一种超声波非介入式液压管路内油液压力的测量方法：以内部充满46号液压油、壁厚2 mm、外径30 mm的钢管为研究对象，使用专业调压设备调整管内液压油压力，利用中心频率4 MHz的宽带超声换能器在钢管外壁对管内的液压油进行探测，并采集不同压力下超声信号，利用短时傅里叶变换同时获得不同压力下超声声速与衰减系数。实验过程中发现：随着钢管内液压油压力的增加，超声声速变大，声衰减系数变大。将超声声速、声衰减系数两个参量与液压油承受压力进行函数关系拟合，从而可以通过声速和声衰减系数计算得到液压油承受的压力值。

1 实验装置

采集超声信号所需的设备资源如下：PC机；奥林巴斯系列中心标称频率为4 MHz的超声换能器；奥林巴斯5072PR型超声信号发射接收仪，可以发射超声波激励脉冲，接收超声波信号并进行信号放大；超声波信号的模数转换采用双通道高速A/D卡PCI-5114，8位有效A/D数据，其采样频率可设置为10、20 MS/s等多种频率，最高可达250 MS/s，满足对中心频率为4 MHz超声波采样要求。实验装置示意图如图1所示。

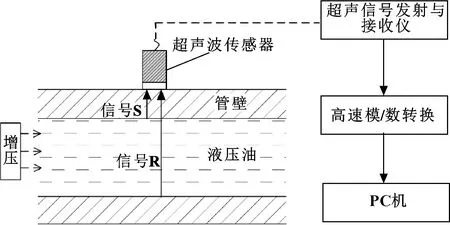
图1 超声信号采集装置示意

实验中所用钢管壁厚为2 mm，外径为30 mm。钢管内充满46号液压油，使用增压设备从两端向管路中液压油施加压力，该设备可以提供1～20 MPa的压力。开启超声波发射接收仪发出高压激励脉冲，激励超声波换能器发射出超声波，将超声波换能器紧贴在管路外壁，待压力稳定后，由超声波换能器接收超声反射信号并反馈回超声波发射接收仪，通过与之相连的高速A/D采集卡，采集超声波回波信号，之后由PC机检测平台进行信号处理，得到所需结果。分别选取钢管上端内壁反射信号S与下端内壁反射信号R为有效信号。

2 短时傅里叶变换

将信号进行傅里叶变换后可以分析信号的频谱，发现信号集中在某一频段，但无法观察单一频率的时间与幅值的关系。短时傅里叶变换(Short-Time Fourier Transform，STFT)的实质是一种加窗后的移动傅里叶变换，将信号从一维时域()分解为二维信号(,)，这种方法可以展示出信号在频域上的信息，同时可以提取单频信号的时间-幅值关系曲线。设信号为()，其短时傅里叶变换的定义为

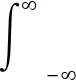
(1)

,()=(-)e-j

(2)

式中：()为窗函数，其定义为

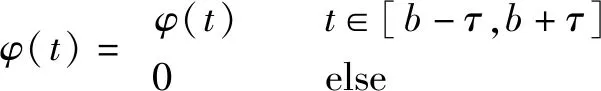
(3)

式中：为某特定时刻;为时间窗函数宽度;为角频率。根据公式(1)—(3)，STFT的过程是：在对信号()进行傅里叶变换之前乘一个时间宽度有限的窗函数()，然后进行傅里叶变换；通过窗函数()在时间轴上的移动，对信号进行逐段分析得到信号的一组局部频谱，将每一个局部频谱进行堆叠后可以得到同时反映信号的时间、频率、幅值特性的三维谱图，该方法称为短时傅里叶变换或STFT。

3 超声声速与声衰减系数的计算

对某一压力下超声信号做短时傅里叶变换后得到其时间-频率-幅值谱，提取某一频率处的时间-幅值谱，信号S和信号R的幅值最高点之间的时间间隔即为在此压力下的传播声时，便可计算出此压力下的超声声速，改变压力，进而得到不同压力下的超声声速。超声声速通过下列公式计算：

=2(-)

(4)

式中：为压力下的超声声速；为管路内径;为超声回波信号R最大值对应时间，为超声回波信号S最大值对应时间。

由超声信号S、信号R在不同压力下的单频信号峰值，计算得到不同压力下的超声衰减系数，从而得到超声衰减谱。超声衰减系数的计算公式为

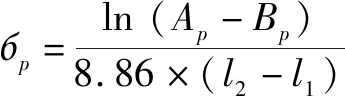
(5)

式中：б为压力下的超声衰减系数；、分别为压力下传播声程分别为和的声波幅值。

4 实验结果与讨论

4.1 信号分析

采用汉宁窗对超声信号作短时傅里叶变换，得到超声信号的时间-频谱-幅值关系图，见图2(a)。分别对1、2、3、4、5 MPa压力下超声波信号做短时傅里叶变换，并提取每个短时傅里叶变换结果的时频谱，如图2(b)—2(f)所示，可以发现，回波信号S与信号R的频率集中在4 MHz附近，并且随着压力的增大，回波信号S与信号R之间时间间隔变小。

图2 超声信号STFT变换结果与时-频谱

以2 MPa压力下超声STFT变换结果为例，分别提取3.4、3.6、3.8、4.0、4.2 MHz单频下的时间-幅度值，如图3所示，可以发现回波信号S、R在3.8 MHz单频信号下的幅值最高。因此，提取2 MPa压力下3.8 MHz单频处信号S、R的峰值，代入公式(4)、(5)计算出声速和衰减系数。

图3 2 MPa压力下不同频率时频谱

对其他4种压力下的超声信号进行STFT后发现，幅值最高点同样集中在3.8 MHz附近。按上述方法分别计算出每种压力下的声速与衰减系数，并作声速谱与衰减谱。如图4(a)所示：同一压力下超声声衰减随频率的增加在一定范围内波动，但整体上相对稳定，这可能是由于数据采集过程中的测量误差引起的。对3.8 MHz频率下的数据进行分析，可以看出超声声衰减随着压力的增加明显变大。这表明：由于液压油体积被压缩，密度和黏滞性都增大，纵波传播过程中声波能量被较多地吸收。由图4(b)可知，同一压力下超声声速随频率的增加基本稳定。同样对3.8 MHz频率下的数据进行分析，超声声速随压力的增加显著提高。这是因为，随着压力的增加，液压油体积弹性模量变大，导致超声在液压油中速度变大。

图4 超声衰减谱与声速谱

4.2 超声声速、声衰减系数与压力的关系

根据表1，对46号液压油压力与超声声速、超声声衰减系数关系进行拟合，结果如下：

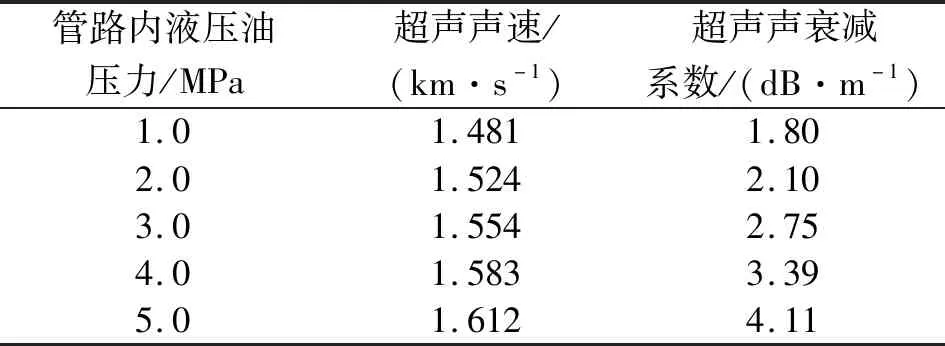
表1 3.8 MHz处不同压力下超声声速与超声声衰减系数

=-9.870 2б+7.729 9б+1.441 1-0.321 1б-

3.942 1

式中：是由声速推算的压力大小；、б分别为频率为3.8 MHz处的超声声速和超声声衰减系数。与、б的拟合相关系数为0.990 3，拟合程度较高，因此可以根据超声参量计算管路中液压油压力大小。

4.3 试验验证

在其他实验条件相同的情况下，将调压设备设定为4.5 MPa，按照前文提到的步骤，得到超声声速谱和衰减谱见图5。由图5得到4.5 MPa压力下频率3.8 MHz处超声声速为1.597 km/s，超声声衰减系数为3.61 dB/m，代入拟合的公式计算得到压力为4.481 5 MPa，相对误差在3%以内，计算结果较准确。

图5 4.5 MPa压力下超声 声速谱与衰减谱

5 结束语

通过短时傅里叶变换法，可以同时计算出超声波在液压油中传播的声速与声衰减系数。在超声声程不变的情况下，随着管路内46号液压油承受压力的增加，超声波在其中传播时，超声声速提高，超声声衰减系数变大。将管路内液压油压力与超声声速、声衰减系数进行拟合后，将超声声速和超声声衰减系数代入关系式，计算得到的46号液压油压力和实际施加在46号液压油上压力的相对误差均在3%以内，计算结果准确，所以用这种方法测量液压系统管路内油液压力是可行的。

目前，国内外非介入式液压系统管路测压方式仍没有成熟的技术，与单纯使用声速反演管路中油液压力的方法相比，同时使用声速与声衰减系数两个参量反演压力应更能反映出油液压力的变化，但还应继续做深入的研究，进一步探究油液承受压力对超声声速和声衰减产生影响的具体原因以及不同种类油液对超声声速和声衰减影响的差异性，以提高该测量方法的准确性、可靠性。