基于面心立方设计的多翼离心风机性能优化*

2022-09-16施旭娜吴宁一吴灵辉肖千豪

风机技术 2022年4期

施旭娜吴宁一吴灵辉肖千豪王军

（1.浙江省健康智慧厨房系统集成重点实验室；2.华中科技大学能源与动力工程学院）

0 引言

多翼离心风机具有风量大，噪声低和结构简单等优点，在民用领域应用广泛，但由于叶片数多且叶道短，其内部流动损失较大[1]，故存在效率低和耗电量大的缺点。由于国家大力倡导“节能、绿色、环保”的发展理念，现代工业已经对风机的性能提出了更高的要求，对风机内部结构参数进行优化，改善其气动性能十分有必要。

近年来，通过将CFD数值计算、数学模型和优化算法相结合，形成了一系列针对透平机械的优化设计方法，大大提高了风机设计的效率[2]。多目标优化的本质是在设计变量的约束范围内通过数学方法寻得目标值的最优解。优化过程中数值计算方法、抽样方法、近似模型和优化算法等因素均会影响结果的准确性。近似模型一般包括响应面模型[3]、克里金模型[4-5]、神经网络模型[6]和支持向量机模型[7]等等。代翠等[8]通过中心复合设计和CFD 数值计算相结合生成样本点，采用响应面模型优化了离心泵的水力和声学性能，降低了泵的噪声水平。肖千豪等[9]采用非均匀B样条曲线对多翼离心风机叶片进行参数化，利用拉丁超立方抽样方法和Kriging 近似模型寻得约束范围内的最优解。李云龙等[10]结合BOX-Behnken 抽样方法和响应面模型对风机的叶轮进出口角和轮径比进行了优化设计，改善了风机的气动性能。黄友根[11]对轴流风机叶片的翼型弦长、翼型圆弧半径和翼型安放角沿叶片径向的分布规律分别进行参数化，采用近似模型和多目标遗传优化算法相结合的气动数值优化策略对模型风机进行了多目标多工况优化设计。姜卫生等[12]将响应面法引入风机蜗壳的优化设计，对蜗壳结构进行参数化，采用中心组合设计生成样本点，优化后的叶轮流道内速度分布更加均匀，涡流区明显减少。张志红等[13]基于发动机连杆装配的例子对比了响应面方法下三类中心组合试验设计（CCDs）在旋转型、稳定性和稳健性三个方面的特征，发现面心立方设计（CCF）的稳健性和模型预测精度均表现较佳。

目前，CCF 抽样方法在风机优化方面的运用较少，而优化过程中样本点的选取代表着整个设计空间，直接影响着优化的精确性和收敛性。为提升风机气动性能并验证面心立方抽样方法的可靠性，本文将对叶轮和蜗壳结构进行参数化处理，采用面心立方抽样试验和CFD 数值模拟相结合的方式生成样本数据，以风机静压和全压效率为优化目标，结合响应面模型和单纯形算法进行寻优。

1 研究对象

本文的研究对象是油烟机系统中的双吸式多翼离心风机，主要结构由油烟机腔体、蝶翼板、滤网、集流器、蜗壳、叶轮、电机、出风罩共同组成，如图1所示。其工作原理[14]为油烟从风机两侧吸入，经集流器整流后沿叶轮轴向流入风机，而后径向流入叶轮，通过叶轮做功获得动压，并流入蜗壳扩压段，经蜗壳扩压后流出，将气体输送至外界。多翼离心风机的主要结构参数如表1所示。

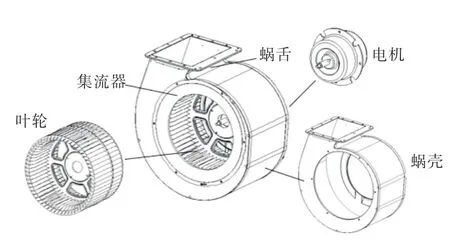
图1 多翼离心风机结构示意图Fig.1 The structure of multi-blade fan

表1 主要结构参数Tab.1 Major structural parameters

本文所研究的多翼离心风机为单圆弧型叶片，合理的叶片安装角会带来气流冲角减小，气体流动损失减少，使得风机的全压和效率升高。蜗舌是蜗壳内部最重要的部件，其附近的流动较为复杂，对风机的气动及噪声特性有较大影响。本次优化将选取叶轮进口角β1、叶轮出口角β2、蜗舌相位角φ和蜗舌半径R作为设计变量，通过调整叶轮及蜗舌结构，达到提高多翼离心风机气动性能的目的。其中，蜗舌相位角是在等蜗壳出口长度L和等蜗舌间隙t的情况下进行调整的，如图2所示。

图2 多翼离心风机结构参数示意图Fig.2 Structural parameters of multi-blade centrifugal fan

2 数值模拟及试验验证

根据油烟机各部件的尺寸，适当简化滤网结构，忽略蜗壳表面的螺栓和螺钉，并省略双吸叶轮的中盘，构建了多翼离心风机流体域模型，如图3所示。流体域模型包括油烟机进口腔体域、蜗壳流域、叶轮域、出风罩和出口延长段五个部分。为保证稳定流动，将腔体进口段和出口段进行相应的延长。

图3 油烟机计算流域和网格划分Fig.3 Computational domain and grid division of range hood system

图3 给出了蜗壳和叶轮的网格模型。由于滤网结构狭面较多且复杂，为保证网格质量，适当增加滤网厚度，以减少由于滤网的不规则性和狭小细面造成的网格数量增多和网格质量的下降。叶轮域是整个多翼离心风机中唯一的旋转域，采用结构化网格，而其他流体域则采用非结构化网格。在叶轮和蜗壳壁面设置边界层。图4给出了最高效率工况下，风机静压随网格数量的变化关系，由此确定整体流域的网格数为564.6万，其中叶轮域的网格数为295.6 万，蜗壳流域的网格数为93.2万。

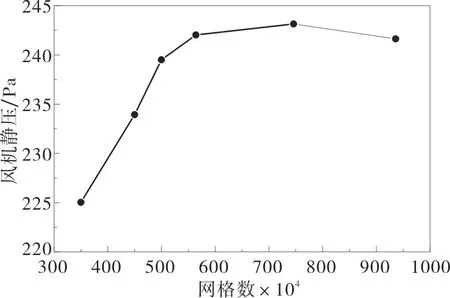
图4 网格无关性验证Fig.4 Mesh independence results

采用Ansys Fluent商业软件来求解Navier-Stokes 方程并获取三维流场。湍流模型选取SST k-ω 湍流模型[15]，给定流量进口和压力出口边界条件，压力与速度耦合采用SIMPLE算法。将叶轮域设置为旋转域，采用MRF多参考系模型，其他区域则设为静止域。流动方程中各项参数包括湍流耗散项、动量方程和湍流动能的离散格式均采用二阶迎风格式。监测油烟机延长段出口截面的全压和静压，当压力波动在5%以内时，认为计算收敛。

图5 给出了原型机压力数值与试验结果的对比情况。数值模拟的风机全压与试验测得的风机全压在最大流量工况下的误差为13%，在最高效率工况下误差在10%，风机全压和风机静压随流量变化的趋势与试验值趋于一致。由于试验测得的效率是风机功率与电机功率之比，而数值模拟算出的全压效率为风机功率与轴功率之比。设轴功率与电机功率之比为电机效率系数ε，故数值模拟得出的效率值需乘以电机效率系数之后方可与试验测得的效率进行比较。图6 给出了原型机效率数值与试验结果的对比情况。本文中电机转速根据不同工况分布在1048～1403r/min之间，而电机效率系数ε 随转速变化的范围在0.5～0.6 之间，取ε 为0.6 进行比较，发现最高效率工况下数值模拟的全压效率和试验测得的效率之间的绝对误差约为2.8%，最大流量工况下数值模拟的效率与试验测得的效率之间的绝对误差约为0.8%。数值模拟的效率曲线与试验测得的效率曲线基本平行。可见气动性能数值模拟的误差均在合理的范围内，能够准确反映压力和效率随流量变化的趋势，数值模拟结果具有较高的可靠性。

图5 原型机压力特性试验与数值结果对比Fig.5 Comparison of pressure between calculated and experimental results under design condition

图6 原型机效率特性试验与数值结果对比Fig.6 Comparison of efficiency between numerical and experimental results under design condition

3 多目标多工况优化设计

3.1 优化流程

图7给出了具体的优化流程，本节将以叶轮进口角β1、叶轮出口角β2、蜗舌相位角φ和蜗舌半径R作为设计变量，采用面心立方抽样试验进行样本设计，基于CFD 数值模拟得到最大流量工况和最高效率工况下各方案的风机静压和全压效率。

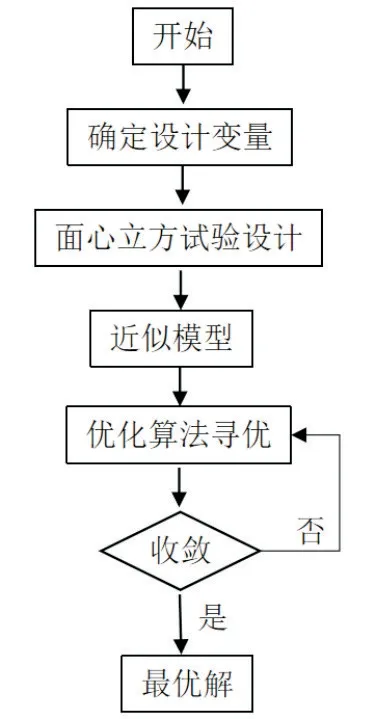
图7 多目标优化流程图Fig.7 Multi-objective optimization process

对两工况下的风机静压和全压效率进行加权，得到加权静压P=0.5Pmvp+0.5Pbep和加权效率η=0.5ηmvp+0.5ηbep，并以两工况加权后的加权静压P和加权效率η作为优化目标，结合响应面模型和单纯形算法进行多目标寻优，得到约束范围内的最优解。数学模型如下：

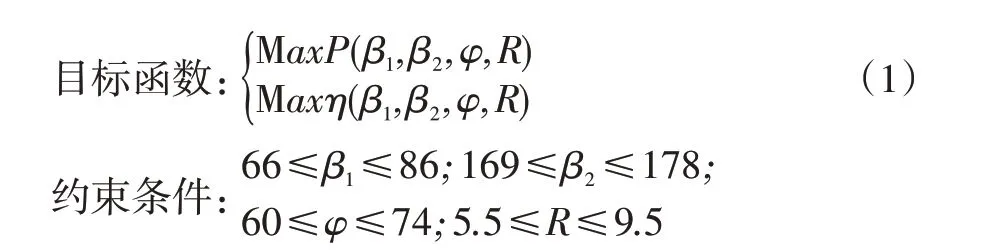
3.2 面心立方试验设计

CCD 对于二阶模型而言是十分有效的试验设计，主要设计参数包括设计中心到坐标试验点的距离α、水平数k和中心点个数nC，而CCF是CCD的一种变形。当α=1时，各坐标轴上所取的点为立方体各个面上的中心点，CCD 的水平数降低，此时的CCD 即为CCF[16]。根据面心立方试验设计方案，对叶轮进口角β1、叶轮出口角β2、蜗舌相位角φ和蜗舌半径R四个设计变量进行抽样方案设计，共29组试验。其中24个试验点为析因点，5个试验点为区域的中心点。表2 给出了试验因子及其水平数，表3给出了面心立方试验设计方案。

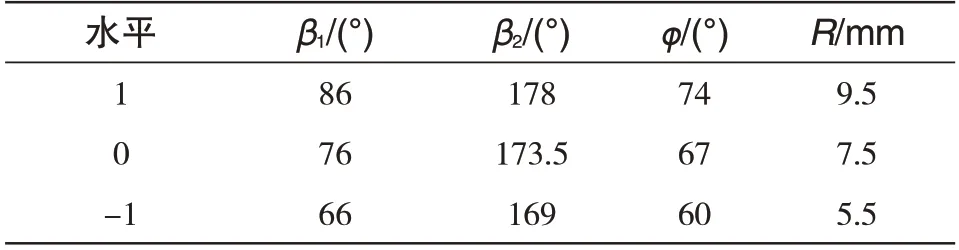
表2 面心立方试验各因素水平Tab.2 Factor levels of CCF

表3 面心立方试验设计方案Tab.3 Central composite face-centered design

通过CFD依次计算不同参数组合方案下最大流量工况（mvp）和最高效率工况（bep）的风机静压和全压效率，具体数据如图8所示。

图8 面心立方试验下两工况气动性能模拟值Tab.8 Numerical results of two work conditions under CCF

3.3 响应面模型预测

对29组试验方案下两工况的风机静压和全压效率进行加权处理，得到加权静压P和加权效率η，采用响应面方法下的二阶多项式对设计变量和优化目标的函数关系进行拟合。选定显著性水平α=0.01，根据F检验可知，回归方程十分显著。加权静压P和加权效率η的复相关系数R2分别为0.87和0.96，表明回归方程拟合精度良好。加权静压P和加权效率η的回归方程系数经四舍五入后表达式如下：

将加权静压和加权效率两个优化目标视为同等重要程度，利用单纯形算法得到最优解，即β1为66.5°，β2为173.6°，φ为71.3°，R为9.0mm。根据回归方程，加权静压和加权效率的预测值分别为138.3Pa和49.2%。

3.4 数值试验验证

通过CFD 数值模拟最优解的气动性能，得到两工况下的静压和效率，如表4所示。对两工况下的风机静压和全压效率进行加权，得到加权静压和加权效率的数值模拟结果分别为135.7Pa和49.31%，响应面模型预测误差低于2%。如图9 所示，优化后风机的静压和效率曲线整体上移，最大流量工况下对应的风机静压增值接近10Pa，全压效率提升了2.37%，说明本次优化提升了风机的最大流量。而最高效率工况下的风机静压和全压效率分别提高了2.4%和1.25%，可见优化效果较为明显。

表4 优化前后压力与效率对比Tab.4 Comparison of pressure and efficiency before and after optimzation

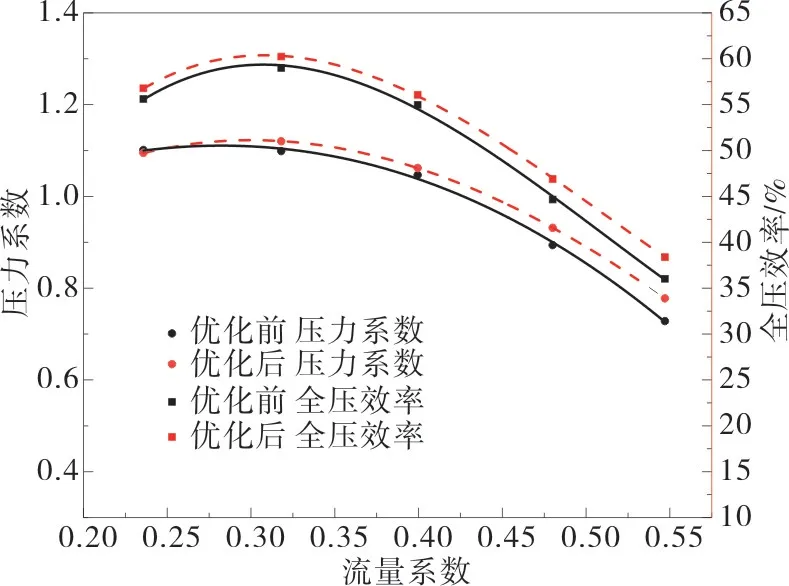
图9 优化前后压力和效率特性对比Fig.9 Comparison of pressure performance and efficiency performance

4 优化前后内流特性

图10给出了优化前后30%叶高处蜗壳截面的内部流动状况。相比于优化前，优化后的叶轮主流区（A 区域）进口气流速度有所提升。叶轮靠近蜗舌上游区域（B区域）的出口速度增大，出口气流主要集中在B区域流出，蜗壳出口扩压段速度相对较小，表明扩压更充分。在最高效率工况下，C区域存在明显的跨叶轮流动现象[17]，优化后的蜗壳内部流线分布更为均匀。可见，优化后的多翼离心风机的内部流动状态相比于原型机有着明显的改善，故而气动性能相应提高。

图10 两工况下速度云图对比Fig.10 Comparison of velocity comtours under bep and mvp

图11给出了两工况下优化前后叶轮的出口径向速度分布。从图中可以发现叶轮的径向速度在蜗舌区域附近有明显的回流（径向速度小于0），蜗壳左侧区域的径向速度分布出现凹陷。优化后两工况下的叶轮靠近蜗舌上游区域的高速流动区增加，叶轮径向速度的分布也更为均匀。φ为0～60°方向上的平均径向速度较优化前在最大流量和最高效率工况下分别提高11.8%和4.3%。