楔横轧阶梯空心轴径向压下量对内孔孔径变化影响规律
2022-09-16屈梦鑫郑书华
屈梦鑫 ,郑书华 ,王 英
(1.宁波大学 机械工程与力学学院,浙江 宁波 315211;2.宁波工程学院 机械工程学院,浙江 宁波 315211)
随着汽车行业的高速发展以及对零件轻量化的要求,汽车轴结构从实心轴向空心轴转变.空心轴相较于实心轴,能降低材料的消耗,进而减少能源的消耗,减小环境污染[1].目前,空心轴有径向锻造、旋转锻造、旋转压缩、内高压成形等成形技术[2],楔横轧技术作为空心轴成形的新兴技术,相较于其他的成形技术,成形效率提高了3 倍以上,材料利用率提升了10%以上[3].
很多学者对楔横轧轧制实心轴和空心轴进行了研究.Bartnicki 等[4]通过两辊轧制实心轴和空心轴,对空心轴轧制的稳定性问题进行了理论研究.Urankar 等[5]研究了楔横轧的失效条件,为后续的楔横轧轧制提供了一定的理论基础.郑书华等[6]通过多楔同步轧制空心车轴,分析了工艺参数对轧制空心轴壁厚均匀性的影响,并通过实验进行了验证.Ji 等[7]研究了工艺参数对楔横轧无芯棒轧制空心轴的影响,确定了轧制空心轴的最佳工艺参数为成形角α=30°~34°,展宽角β=5°~7°,断面收缩率ψ=65%~70%.江洋等[8]通过研究楔横轧成形厚壁空心轴件,得出了成形过程和金属流动规律.Shen等[9]提出了加工变内径空心轴的新工艺,分析了变内径空心轴的金属流动、内台阶成形工艺、芯棒补偿,使内孔尺寸可以得到有效控制.Zhou 等[10]通过有限元模拟和实验研究了内径的均匀性,得出内孔尺寸波动的主要原因是金属流动不当.
以上都是针对单台阶轴进行的研究,而对阶梯轴楔横轧的研究较少.韩素涛[11]研究了多台阶无料头精确成形理论,建立了多台阶轴的有限元模型,为本文有限元模型的建立提供了一定的理论基础.路红岩等[12]研究了楔横轧多台阶轴的轧齐曲线,华军等[13]研究了楔横轧复杂大断面多台阶轴的拉细缩颈问题,Pater 等[14]使用了斜轧工艺生产阶梯式车轴,Han 等[15]研究了楔横轧多台阶轴工艺参数的多目标优化,这些研究都限于实心阶梯轴.
为了更好地控制内孔质量,本文针对阶梯空心轴的楔横轧成形过程进行了有限元模拟和实验研究,分析了阶梯空心轴成形过程中的金属流动规律、径向压下量影响内孔孔径变化的规律、不同的原始相对壁厚Q和轧制温度T条件下径向压下量影响内孔孔径变化的规律,并通过实验验证了有限元模型的正确性.
1 楔横轧阶梯空心轴的数值模拟
1.1 有限元模型的建立
阶梯空心轴的加工图如图1 所示.在刚塑性有限元软件Deform-3D 中对阶梯空心轴进行分析,其有限元模型如图2 所示.在建立有限元模型中做出如下设定: (1)模具、导板定义为刚体,轧件定义为塑性体;(2)采用轧件的1/2 进行模拟仿真,且在对称面上施加约束,减少模拟所需要的时间;(3)模具与轧件之间采用剪切摩擦,设置为2.0;(4)轧辊与轧件的热交换系数和轧件与环境的热交换系数为常数;(5)轧件采用六面体网格单元进行划分.
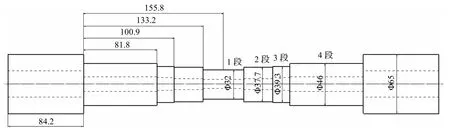
图1 阶梯空心轴(单位: mm)
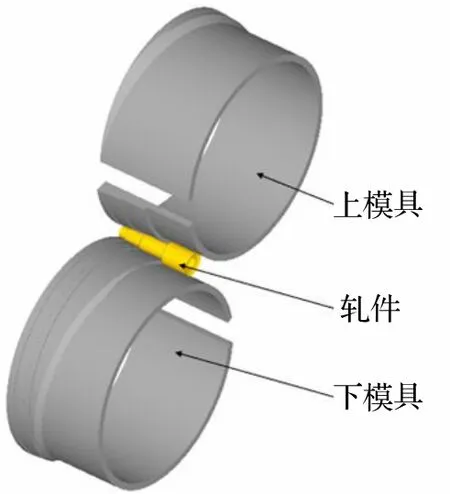
图2 阶梯空心轴的有限元模型
1.2 工艺参数的选择
采用42CrMo钢作为轧件的材料来研究阶梯空心轴的成形过程.42CrMo 钢作为常用的空心轴材料之一,其应力应变曲线由文献[16]可知.本文采用的阶梯空心轴的各项参数如图1 所示,其有4 个断面收缩率,分别为76%、66%、63%、50%,对应的长度分别为22.6、32.3、19.1、81.8 mm,将其设定为1 段、2 段、3 段、4 段.在设计模具的过程中,根据文献[11,17],要结合各个断面收缩率所对应的成形角与展宽角,轧制出符合要求的阶梯空心轴.结合文献和工厂的生产经验,本文采用成形角α为30°,展宽角β为6.8°进行模拟仿真.坯料长度L为315 mm,轧件初始外径D0为65 mm,轧制后的外径D1、D2、D3、D4分别为32.0、37.7、39.3、46.0 mm,对不同的内径可以计算得到不同的轧件原始相对壁厚Q,
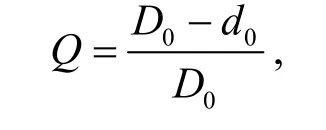
式中:D0为轧件初始外圆直径;d0为轧件初始内孔直径.
2 楔横轧阶梯空心轴的成形研究
2.1 阶梯空心轴的成形过程
以轧件相对原始壁厚Q=0.55,轧制温度T=1 180 ℃的工艺条件进行模拟计算.
图3 为随轧制过程的进行,在不同时间点的阶梯空心轴的成形过程.
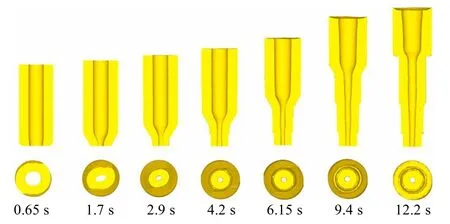
图3 楔横轧阶梯空心轴成形过程
在0.65 s 时,轧辊上的楔形模具开始楔入1 段,轧件开始变形,包括沿轴向进行拉伸变形和沿径向进行挤压变形.之后直到2.9 s 时,随着轧辊的不断楔入,轧件变形逐渐从外层向内层传递,内孔的形状不断发生变化,内孔总体尺寸缩小.到4.2 s 时,轧件1 段进入精整段,内外表面逐渐过渡到规则的圆形,轧辊开始楔入2 段.随着轧辊的继续楔入,轧件在径向上继续受到轧辊的挤压,并逐步楔入3段,同时轧件的1、2 段进行精整,逐渐趋于圆形.同理,到9.4 s 时,轧辊楔入4 段,轧件1、2、3 段进行精整.到12.2 s 时,轧件的1、2、3、4 段都进行精整.精整后,各个阶梯上的内外表面最终变为圆形.
2.2 阶梯空心轴成形过程的金属流动规律
图4 为阶梯空心轴的轧前轧后追踪点分布.轧前分别在各个台阶处取一个截面,并在每个截面上从内孔到外圆取7 个点(图4(a)),分析阶梯空心轴上从外表面至内表面的金属流动.图4(b)所示为轧后的追踪点分布.
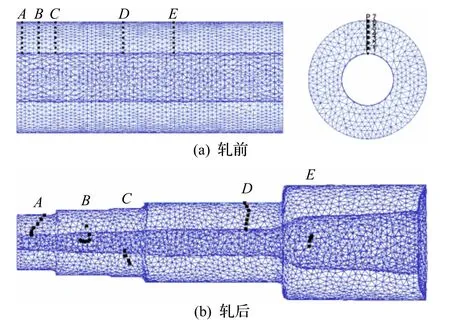
图4 阶梯空心轴的轧前轧后追踪点分布
图5 所示为阶梯空心轴轧件追踪点的径向位移与轴向位移.
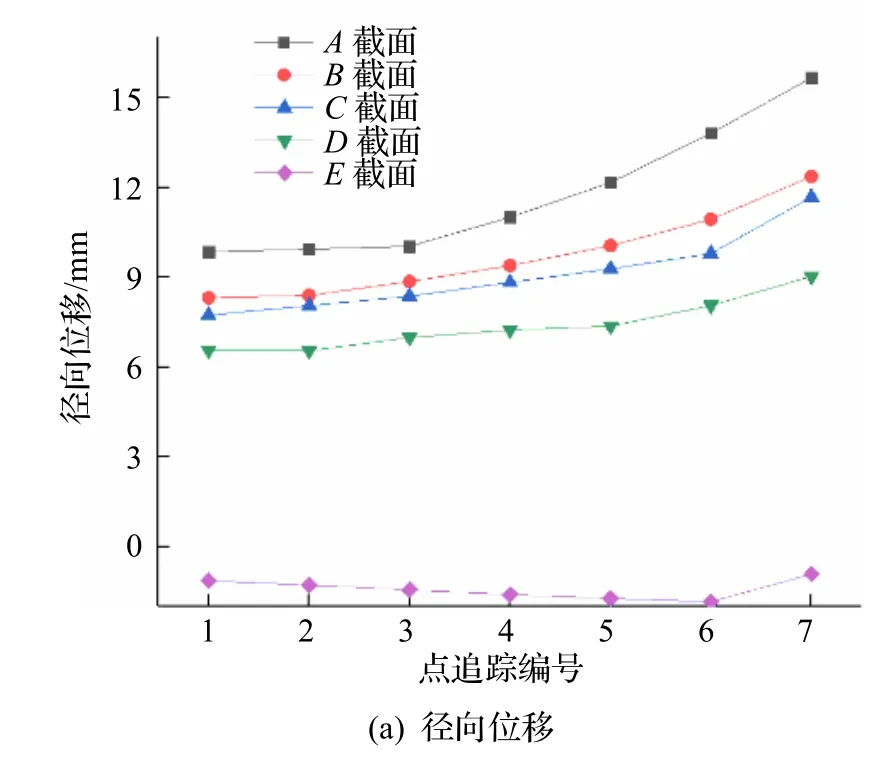
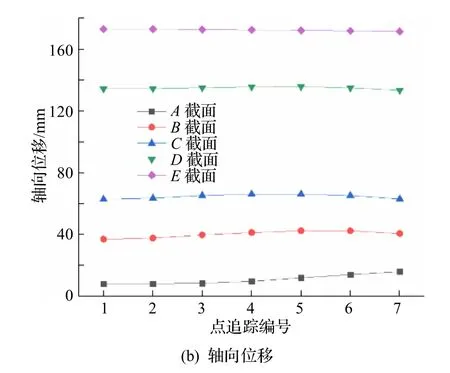
图5 轧件追踪点的位移
从径向位移图(图5(a))可以看出,在同一截面上,从内孔到外圆,径向位移越来越大.其原因是内孔的径向变形是随着外圆的径向压下而逐渐变化的,始终小于外径的压下量.而随着径向压下量的增大,在外圆和内孔上,轧件的径向位移都会相应增大.截面E在轧制过程中属于料头部分,不产生径向压下变形,但由于其他段轧制变形导致的轴向位移变化,使其在轴肩部位出现微小隆起,表现为负值的径向变形.
从轴向位移图(图5(b))可以看出,轧件的轴向位移在A截面上从内孔到外圆会相应地增大一些,原因是在轧辊楔入的过程中,外圆先进行变形,继而带动内圆变形,因而外圆的轴向位移大于内圆的轴向位移.从B截面到D截面,轴向位移从内孔到外圆先增大后减小,原因是外表面受到轧辊与轧件之间的摩擦力,对外表面金属的轴向流动产生了阻碍作用.在E截面,由于未进行轧制,各追踪点上的轴向位移基本保持不变.在轧件外圆处,从A截面到E截面,轴向位移逐渐增大,原因是截面离对称面越远,则受到轧辊给予的轴向力作用时间越长,轧件的轴向位移越大.
3 楔横轧阶梯空心轴径向压下量与内孔孔径变化的关系
楔横轧轧制阶梯空心轴属于复杂的变形,每一级台阶对应的断面收缩率不同,径向压下量不同,轧制后的内孔也会产生不同的变化.探究阶梯空心轴径向压下量与内孔孔径变化之间的关系可以对一定的径向压下量下内孔孔径的变化进行预测.
3.1 径向压下量与内孔孔径变化的定义
轧件的径向压下量指的是轧件初始外圆半径与在一定时间内轧件经轧辊加工过程中外圆半径之间的差值,即:
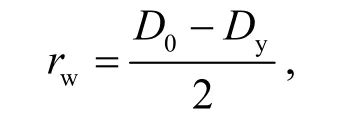
式中:rw为径向压下量;Dy为轧件经轧辊加工过程中外圆的直径.轧件各参数如图6 所示.
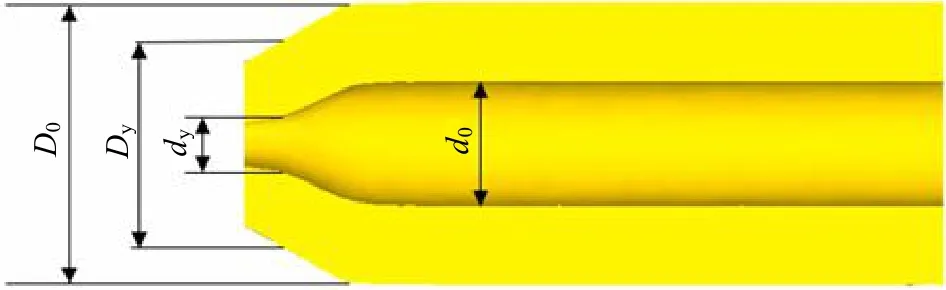
图6 轧件各参数位置图
轧件的内孔孔径变化是指轧件初始内孔半径与在一定时间内轧件经轧辊加工过程中内孔半径之间的差值,即:
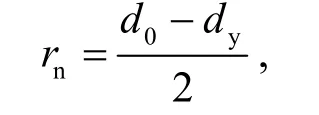
式中:rn为内孔孔径变化;dy为轧件经轧辊加工过程中内孔的直径.
3.2 阶梯空心轴中径向压下量与内孔孔径变化的关系
基于上述模拟计算的结果数据,分析阶梯空心轴中各截面在不同的径向压下量下内孔孔径变化的规律.
在上述算例中,阶梯空心轴的4 个断面收缩率76%、66%、63%、50%分别对应图4 的A、B、C、D截面.提取仿真过程中外圆与内孔的直径,计算径向压下量与内孔孔径变化量,进行数据处理分析后,建立图7 所示的各截面随时间变化径向压下量与内孔孔径变化离散点分布,并利用MATLAB进行数据拟合,采用二项式拟合方式得到的曲线多项式分别为:
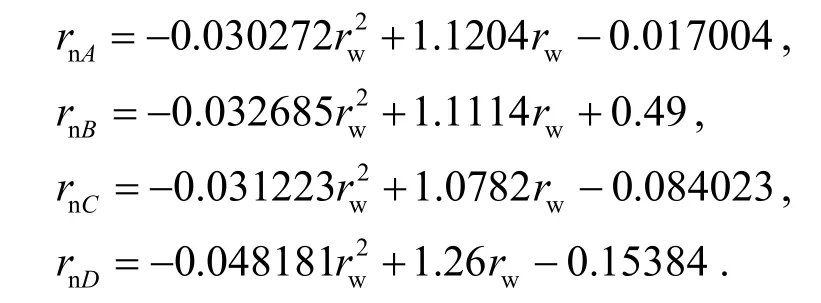
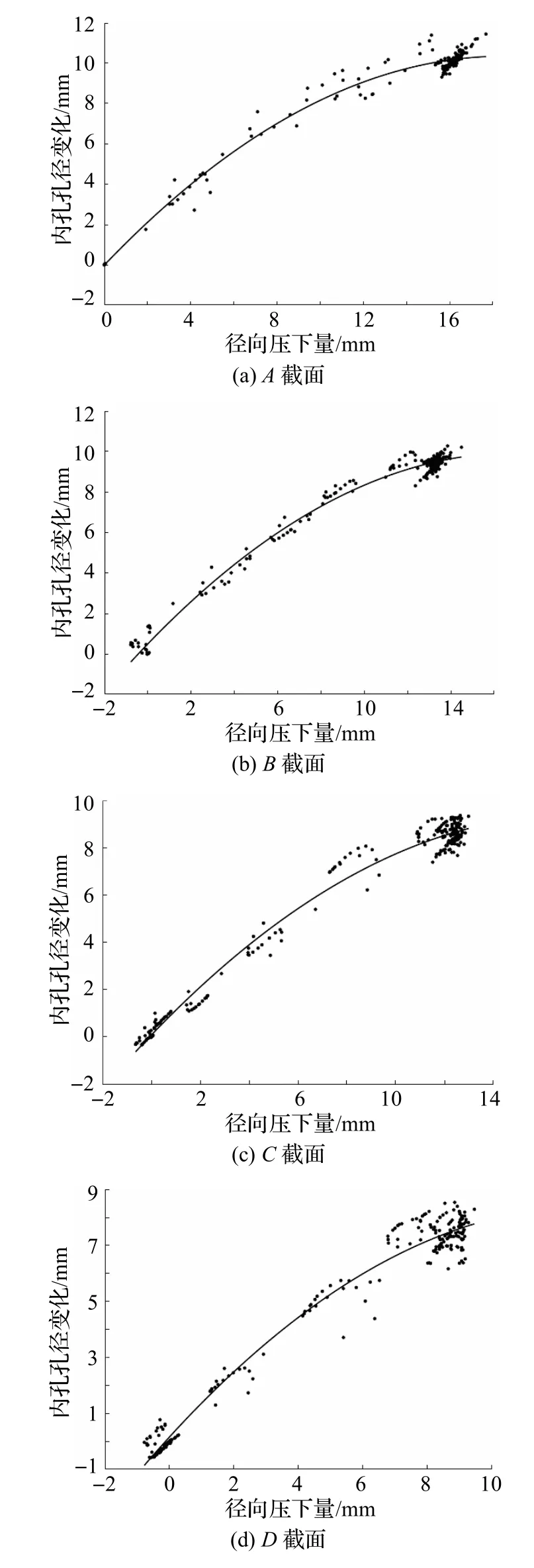
图7 各截面随时间变化径向压下量与内孔孔径变化的关系散点分布与拟合图
对比各个拟合多项式可以看到,对于阶梯空心轴楔横轧变形,当断面收缩率为76%、66%、63%时,可以将各拟合函数在较小的误差范围内统一归结为,即径向压下量与内孔孔径变化的关系式;而在断面收缩率为50%时,其拟合函数表现出的内孔变化随着径向压下量的变化比其余断面收缩率的统一拟合函数偏大一些.
3.3 原始相对壁厚的影响
原始相对壁厚在测量阶梯空心轴径向压下量与内孔变化之间的关系方面至关重要,在相同径向压下量的情况下,它直接影响了内孔孔径的变化.因此,本文探究了在不同轧件原始相对壁厚的情况下径向压下量与内孔孔径变化之间的关系.不同轧件原始相对壁厚的有限元模拟的工艺参数见表1.

表1 有限元模拟的工艺参数
图8 所示为在不同轧件原始相对壁厚下径向压下量与内孔孔径变化之间的关系.由图8 可知,在相同径向压下量下,内孔孔径变化随着原始相对壁厚的增大而减小,且在径向压下量为9.5 mm,原始相对壁厚为0.67 时,内孔孔径变化最小,其值为3.34 mm.产生原因是当径向压下量较大时,断面收缩率较大,轧件外部塑性变形较大,轧件径向力较大,轧件内部的塑性变形较大,轧件的内孔变化也就较大.
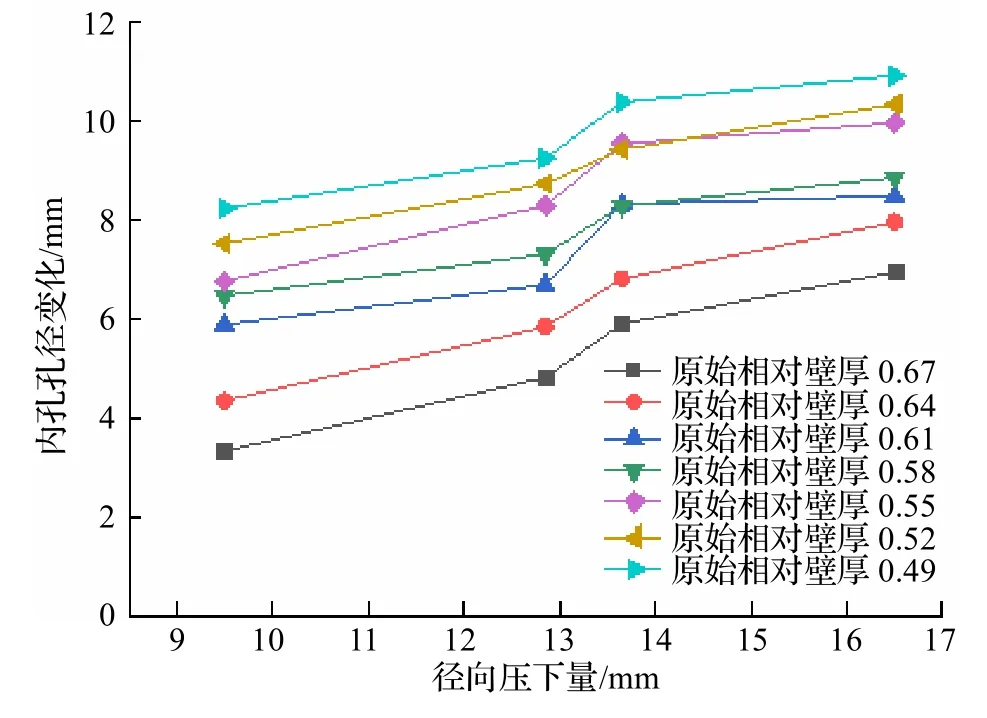
图8 原始相对壁厚的影响
3.4 轧制温度的影响
轧制温度T对阶梯空心轴的径向压下量与内孔孔径变化之间的关系也有重要的影响.由图9 可知,当轧制温度T=1 050 ℃时,在径向压下量为16.5 mm 的情况下,内孔孔径变化最大,最大值为10.27 mm.当轧制温度超过1 050 ℃时,相同的径向压下量下的内孔孔径变化减小,原因是随着轧制温度的升高,变形抗力减小,轧件受到的径向力与切向力增大,轧件更容易被压扁[18],导致轧制后内径的增大,使内孔孔径变化减小.当温度低于1 050 ℃且持续降低时,轧件的变形抗力增大,轧件受到的径向力与切向力减小,轧件的径向流动性变差,使内孔孔径增大,内孔孔径的变化减小.
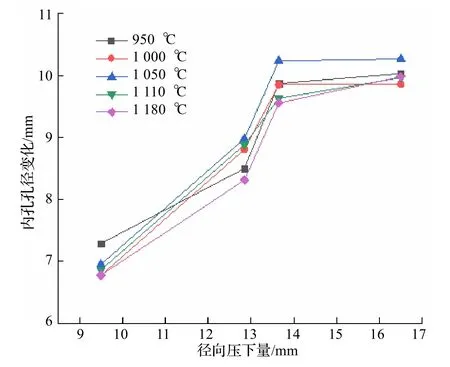
图9 轧件轧制温度的影响
4 阶梯空心轴轧制实验验证
为了验证阶梯空心轴模拟仿真的准确性,采用轧辊直径为800 mm,轧辊长度为700 mm,轧件最大直径为80 mm,轧件最大长度为600 mm 的H800 楔横轧机对阶梯空心轴进行实验验证,如图10 所示.实验采用的模具参数与轧件参数见表2.图11 为阶梯空心轴轧制后的纵剖面,图11(a)为模拟结果,图11(b)为实验产品.从模拟结果与实验产品可以看到,轧件外形都成功形成了阶梯形,具有相似的轧后内孔形状.对比模拟结果数值以及实验产品的外形内孔测量值,如图12 所示.对比可知,外圆模拟值与实验值在1 段上相差最大,其误差值为4.3%;内孔模拟值与实验值在3 段上误差最大,其误差值为4.6%.因此模拟值与实验值都吻合良好,轧件的径向压下量与内孔孔径变化关系也表现出一致的变化趋势和较好的重合度.

图10 H800 楔横轧机
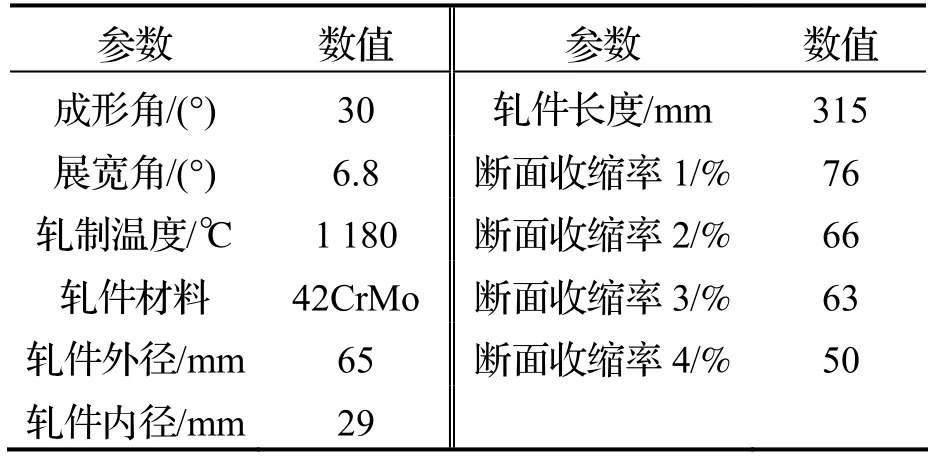
表2 实验的各项参数

图11 阶梯空心轴的轧件形状
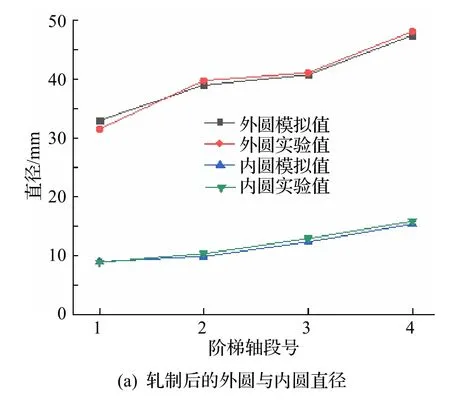
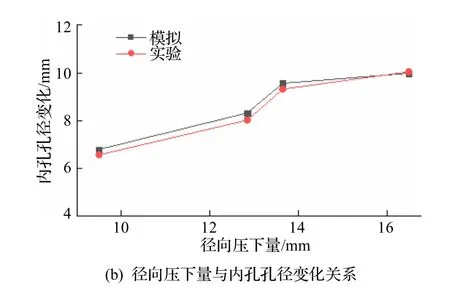
图12 模拟与实验结果对比
5 结语
(1)建立了阶梯空心轴楔横轧成形过程的有限元模型,分析了阶梯空心轴的成形过程和金属流动规律,利用MATLAB 实施数据拟合,获得了阶梯空心轴中径向压下量与内孔孔径变化的关系模型: 在断面收缩率为76%、66%、63%时,其径向压下量与内孔孔径变化可以归结为rn=+1.1rw.
(2)阐明了在一定的径向压下量下,内孔孔径变化随着原始相对壁厚和轧制温度变化的规律:随着原始相对壁厚的增大,内孔孔径变化减小;随着轧制温度的升高,内孔孔径的变化先增大后减小.
(3)楔横轧实验样品的测量结果与模拟仿真结果吻合良好,误差在4.6%以内,表明所建立的有限元仿真模型可以为阶梯空心轴的楔横轧生产提供参考.
