数形结合在小学数学解题中的运用策略探究

福建省三明学院附属小学 廖加庆

数形结合具体指的是根据数形间的相应关系，通过有效转化数形来进行问题解决的一项思维方式。新课程背景下的“数形结合”思想，贯穿整个小学数学教学。目的在于对学生逻辑思维能力的培养与提高。

一、数形结合在小学数学解题中运用的意义

教师在小学数学教学解题中运用数形结合的方式可以将数学问题通过图形直观地呈现出来，有利于学生探索空间的扩增，促使学生能够由不同层级以及角度来开展逻辑思维活动。在进行数学问题解答时教师利用直观的图形来呈现出抽象的数量问题，可以让学生更为清晰地掌握不同知识点间的逻辑关系，让其更容易理解问题，并且可以引导学生利用掌握的知识以及学习经验来进行分析与归纳，得到一个较为全面的解题思路，对于其解题效率以及质量的提升有着非常积极的现实意义。

二、数形结合在小学数学解题中的运用策略

1.运用数形结合使学生养成良好习惯。

良好的习惯是成功的一半。数形结合是我们在数学解题中最常用、最有效的思想方法。数形结合解题能力的培养也是我们数学教师课堂教学内容的一部分和努力的方向。如在教学“鸡兔同笼”的过程中，我们采用假设法解题时，教师单纯地用语言一直强调鸡和兔两个变量的变化，效果肯定不是很显著，若用数形结合，通过学生想一想、画一画、再想一想、再画一画，帮助学生理解题目中鸡和兔这两个变量，从而引发学生的联想，启发孩子的思维，把化繁为简、化难为易的思想方法深入孩子的心理，潜移默化中悟出画图方法的好处，感受到数形结合的优点，为学生良好的学习习惯奠定基础。

2.运用数形结合来理解抽象概念。

因为在小学数学中许多概念都比较抽象，但是小学生因为生活经验不足，且抽象思维受限，所以理解起来难度较大。因此教师可以合理渗透数形结合的方法理念，合理转化图形与数据，直观地呈现出抽象的数学概念，提高学生的学习效率和解题能力。如在一年级上册“认位置”学习过程中，教师可以设计以下几个题目：①一年级小朋友在排队，小明前后分别有3人与6人，总共有多少名学生在排队？②有一些小朋友在排队，由前到后数，小丽是第三位，由后往前数，她是第六位，排队的小朋友一共有多少位？在解答题目①时，算式为3+6+1=10；解答题目②时，列出算式：3+6-1=8。在解答这两道题时，较易导致学生思维混乱，分不清楚是要在什么时候“+1”，什么时候“-1”。所以教师能够采取属性结合的方法，把学生用圆圈代替，并在黑板上画图，让学生能够直观地了解到什么时候“+1”，什么时候“-1”。通过数形结合的方法可以让学生通过图形掌握本质内容，将直观地画圆圈数数的方式呈现出排队的问题，让解题变得更为直观与简单。

3.运用数形结合来理解算理与算法。

因为数和形存在着非常密切的联系，在学习数学运算定律时教师可以合理运用数形结合的方式来帮助学生理解运算定律，正确使用计算方法，直观地呈现出抽象的数学概念。例如，在对“乘法分配律”进行教学过程中，在开展简易计算估测中，一些学生使用乘法分配律往往会出现错误，并不会深究其原因，也没能正确认知相应的算理。在小学阶段，学生的思维由具体形象思维转变为抽象思维，而在学习乘法分配律时存在一定的抽象性，所以学生学习起来存在一定难度，所以教师能够利用属性结合的方式，通过面积解题的方法来让学生对运算定律有一个更深刻的理解。又如，“真分数与假分数”这部分内容的重点是加强学生对分数的认知，在此之前学生应掌握了分数的意义以及相关的内容，因为真假分数这一知识概念具有较强的抽象性，所以知识采取单纯的讲解教学难以获得理想效果。所以教师可以运用数形结合的理念，引导学生联系其直线上点以及图形，利用“1”作为分解，让学生对真分数与假分数进行判断。不过在此过程中学生可能会出现认知上的偏差，所以，教师能够引导学生回忆之前学习过的分数知识，随后应用“面积模型”，采取画阴影的方式来代表分数，这样学生能够更易于理解。

4.运用数形结合来建设动态图形表征。

运用数形结合建设起相应的图形表征，能够让学生在观察图形过程中将新旧知识充分融合起来，循序渐进地掌握算例，运用算法，获得正确的解题思维，从而可以促使学生在解题、推理、假设以及验证环节能够自主理清思路，将相关知识内容有效联系起来。例如在解答题目“小铭、小莉还有小红一起吃相同蛋糕，其中每人吃了个，请问这三人总共吃了多少个？”通过问题来将算理分数与整数相乘引出，引导学生在自主思考以及运算推理中更好地掌握并优化解题步骤与方法，正确认识分数乘法的意义，并熟练运用相关计算法则。因为该道题中存在比较抽象的数量关系，学生难以展开深入的思考，所以教师能够运用方格图形来将问题结构直观地呈现出来，减小解题难度，能够让学生根据自己掌握的知识经验，经过思考、对比来对整数乘法有一个大致的理解。由此可以发现，抽象的数量关系能够利用图形直观清楚地呈现出来，有利于学生能够在实质上理解分数乘法，此时教师还可利用图形来引导学生由图形处理的层面逐步深入的联系起分数乘法算式和图形。教师通过提问“是否还有更为简便的方法来计算出来引导学生将图形表征有效结合起来。“每位同学分别吃了，也就是两个，那么三位同学总共是吃了六个，所以这道题最终目的是要算出3×。不仅如此，教师还应当要引导学生对其运算所得的结果进行分析与参数，让其能够更为透彻地掌握解题步骤，了解题目中给出的已知条件，进而更好地掌握分数和整数乘法的意义所在。3×也就是将三个加起来，学生通过将加法向乘法算式转换，并进行图形分析能够正常进行解答由此也更好地掌握了分数与整数相乘的意义。在解题过程中运用数形结合的思想要求教师能够关注学生空间想象力以及几何直观能力的培养，让其在动手实践过程中进行分析与思考，让其能够利用图形更好地发现与掌握数学规律。

5.运用数形结合创设解题情境。

在小学数学教学中合理利用图形能够有利于学生思维的发散与开阔，加深其对相关数学知识的理解与影响，所以在解题过程中教师需要重点提高学生利用图形来分析并处理问题的能力。为了有效吸引学生注意，调动其解题积极性，教师可以利用多种直观图形来创设多元化的学习情境，并将数学运算的定律呈现出来。因为学生在解题时能够完成知识经验的建设，教师需要围绕学生思维、判断、辨别等能力的提升来引导其联系实际生活经验来进行解题，通过利用图形结构来将数量关系反映出来不但能够提高学生对数学概念的理解，而且还能让其体会到实际生活重视数学的重要价值。如在对“百分数的认识”学习过程中，教师可以给予学生已有的生活经验来创设相应情境，让其得以在灵活转变数据和图形过程中正确掌握百分数和分数间的差别，并了解到生活中百分数的有效作用：“许多同学都喜欢喝苹果汁，某类饮料中苹果汁含量是55%，请问苹果汁含量是55%是什么意思？___是___的55%？连续地追问，引发学生对生活中的问题进行思考。并将这55%在方格中呈现出来”学生回答出来后教师可以进一步提问，“苹果汁含量还可以再多点吗？能够达到110%吗”引导学生利用表格中的数据与信息来思考苹果汁含量能否大于100%。学生通过直观的图形观察与分析能够快速理解数量关系以及认识到百分数是属于部分与整体比较的关系，一定是在100%以内。因为数量关系对于小学生而言比较抽象与乏味，学习难度较大，所以难以提起学习兴趣，因此要求教师能够基于学生已有的知识以及生活经验，合理运用数形结合的方式来促使学生探究在图形中所蕴含的数量关系以及已知条件，让其能够在绘制、观察、分析以及推理图形时体会到问题解决的快乐，提高其学习兴趣与自信。

6.运用数形结合做好图形结构的分析。

数形结合一个显著特征在于能够实现抽象问题的精简化以及直观化，在解题过程中教师可以有意识地引导学生在归纳与分析图形时自主反思学习成果，并且在掌握数学规律时能够充分融合新旧知识，构建起较为系统的知识架构，提高其数学问题的解答效率。如，在对“扇形统计图”进行学习过程中，相关数据能够利用扇形统计图来呈现出来，引导学生通过分析图形数据来对其变化情况与规律进行分析与总结，正确认识到扇形统计图中所呈现出来的总数和部分数量的关系。如，教师可以利用扇形统计图来将牛奶的营养成分呈现出来，如图1所示。同时引导学生独立思考，让其能够在观察与分析过程中将回忆学习过的知识，并将条形统计图的特征与之相联系，形成较为全面的数据分析概念。不仅如此教师还能够利用百分比的实际含义来鼓励学生将学习过的折线统计图、条形统计图以及百分数等知识相联系起来，以更好地理解扇形统计图的特征还有其在生活中的实际应用，促使学生将数学知识与实际生活相联系起来。

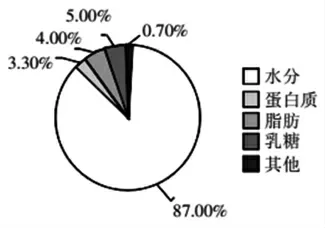
图1 牛奶营养成分扇形统计图

由于小学数学中会学习到许多基础性的几何知识，学生在进行学习时往往是根据实物为基准，也就是说停留于表象上的认识。所以教师应当要注重学生空间知识体系的建设，引导学生将有关的集合知识进行总结与归纳，形成完善的知识架构，这样能够有利于其空间观念的形成，提高知识的应用能力。例如，在“圆的面积”学习中，教师不能单纯让学生死记圆的公式，一定要让学生回忆如何推导出已经学过平行四边形、三角形、梯形等平面图形的面积，接着使用有关圆的教学器具，引导学生会用剪拼、割补法来拼凑成已经学过的长方形，掌握相应的转化思想，这样就能够让学生可以串联并运用起之前学习过的知识内容，为今后数学的学习打好基础。

7.运用数形结合提高解决问题能力。

解决问题是小学数学教学的一项重要内容，但是不少学生都会对解决问题存在恐惧心理。因为其具有一定的复杂性，学生极易弄混题目条件，读不懂其相关信息的联系。但是在解答该类题目时应用数形结合的方式就能够有效防止该类情况出现。

在解题时，教师可以引导学生在读取每一条件时，就合理转化“数”和“形”，理清解题思路。如，在学习“计算多边形面积”过程中，教师可以设计这样的应用题“商店售卖的三角巾是等腰三角形，其高与底均为9分米，现有长方形布料，宽度为18分米，长度为72分米，那么最多可以做出多少块这样的三角巾？”大部分学生很快都能写出72×18÷（9×9÷2）=32。此时教师可以进一步引导学生思考其他解决方法，提示学生能够利用数形结合的方式来进行，学生通过互相交流与分析，按照题目意思来绘画出相应的示意图，从而得到72÷9×2×（18÷9）、72×18÷（9×9）×2以及72÷9×（18÷9）×2这几种算法。在解题过程中应用数形结合的方式可以有助于学生快速分析出题内的数量关系，将解题难度降低，有利于学生数学思维的发散。又如，在“植树问题”教学中，借助生活中的实例，如路边的大树、路灯、手指课件演示，在该课教学中把一一对应数学思想方法作为支点，从而引出间隔与间隔数，为新课学习作铺垫。课前我出示“为了美化环境，在500m的道路两端种植树木，每棵树木间距为5m，总共需种植多少棵树木？”我从学生已有的经验出发，要求学生来画示意图来模拟种树，再将学生画的示意图让学生展示交流。根据学生之间展示的示意图，再结合一一对应思想，突出了数形结合的思想，将抽象的数学语言与直观的图形相结合，让学生感受生活中处处有数学知识，也利于学生的理解和掌握。这就加强了数与形之间的联系，利用数形结合，让学生体验到提出、思考、分析并解决问题的过程，让其发现并掌握解题技巧，提高其数学应用能力。

总之，新课程背景下的“数形结合”思想，它贯穿整个小学数学教学。而小学数学教学的目的在于对学生逻辑思维能力的培养与提高，尤其是空间形式与数量关系是学习的重点内容。诸多数学问题的解答均为根据“数”和“形”来展开，正如著名的数学家华罗庚所说：数缺形时少直观，形少数时难入微。所以教师们在进行数学教学、解题过程中都需要注重运用数形结合的方式，将抽象、复杂的问题形象化与直观化，让学生更容易理解与掌握，激发学生学习的兴趣，提高学生的数学学习能力。