面向常发性拥堵的城市局部路网韧性评价与分析*

陈思妤 李洁▲ 胡演诚 姜宇

（1.湖南大学土木工程学院 长沙 410082；2.丹麦科技大学管理工程系丹麦 灵比 2800Kgs）

0 引言

韧性的概念最早出现在生态系统领域，现已延伸至社会学、灾害学、心理学等各方面[1]，并引起许多交通学者的关注。城市交通系统韧性被定义为系统抵抗、减少，以及吸收干扰（冲击、中断或灾难）影响的能力，保持可接受服务水平（静态韧性），以及在合理的时间和成本内恢复正常和平稳运行的能力（动态韧性）[2]。交通系统韧性反映了系统在扰动下的恢复速度及恢复原有功能状态所需的外部援助量[3]。交通基础设施韧性是指从容应对中断事件，并在合理时间范围内将自身恢复到不低于中断前服务水平的能力[4]。交通韧性研究多针对偶发事件对交通系统的影响，比如，涝灾[5]、地震[6]、飓风[7]等极端天气，以及恐怖袭击、交通事故[8]等紧急公共事件对路网造成的冲击。考虑到机动车持续增长不仅带来延误和经济损失，还导致能源消耗、废气排放、交通噪音的增加等，从韧性角度提出衡量路网承载车流能力的替代方法。一般而言，拥堵分为常发性和偶发性（特殊事件），前者在很大程度上影响道路日常运营，是产生城市交通延误的直接原因。因此对交通状态进行有效评价是城市交通管理的1项重要任务[9]。

“冲击”一词不仅指代猛烈的撞击，还比喻导致系统性能短时间内产生巨大变化的干扰或打击。车流量在短期高峰时段内持续增长，路网的扰动不断加剧并随时空演变逐渐扩散。短时激增流量对路网产生干扰打破了原有交通平衡状态，引发车流运行状态波动，与韧性中的“冲击”内涵一致。因此“冲击”包括但不局限于不可预测、偶发性事故（如风雪，冰雹，地震等）、路段中断等情形，还可形容高峰时段大量车流对路网的影响。综合文献对韧性的定义，把考虑常发性拥堵的城市局部路网韧性定义为：路网在运营中受到周期性流量冲击时具有一定的缓冲能力，可通过自身设备调节优化提高吸收大量车流冲击的性能。

道路韧性评价可分为路段层面与路网层面。对于路段层面评价，Tang等[10]为了分析常发性拥堵给路段带来的延误问题，将经常性拥堵视作内部干扰，提出基于韧性三角形曲线的多个改进指标（弹性阈值、鲁棒性范围、拥挤程度、拥挤时间、阻力系数、拥堵指数、服务水平等），用以捕捉路段拥堵模式。对于路网层面，部分研究探讨了交通流异质分布对路网整体韧性的影响。吕彪等[11]定义了基于日变交通配流（day-to-day traffic assignment，DTA）的路网可达性指标，构建全面评价扰动事件生命周期内系统性能的韧性指标与评价模型。研究发现与传统随机用户均衡模型相比（stochastic user equilibrium，SUE），DTA模型能够更准确地反映扰动下路网流量分配情况，得到更符合实际的韧性指标。Murray-tuite等[3]从适应性、安全性、移动性和恢复性4个方面分析系统韧性，并在测试网络中比较了系统最优（system optimum，SO）和用户均衡（user equilibrium，UE）配流对系统韧性的影响，发现UE能带来更好的适应性和安全性，而SO能带来更好的移动性和快速恢复性。

此外，有研究采用宏观基本图（macroscopic fundamental diagram，MFD）评价交通网络韧性。Amini等[12]基于MFD定义加权空间平均流量与平均行驶距离之比为完成出行的绩效指标，并认为路网韧性指数是正常情况下和异常事件下绩效指标的差值。该指标能反映事件发生前后网络的车流出行完成量，评价交通管控的效率。Kim等[13]对比正常和事件情况下的MFD曲线，基于MFD的脆弱性指数（MFD-based vulnerability index，MVI）评价城市道路韧性。Hoogendoorn等[14]基于广义宏观基本图（generalised macroscopic fundamental diagram，G-MFD）确定路网服务水平，以特定事件下路网服务水平变化评价韧性。

无论是在路段还是路网层面，韧性的多指标评价因为指标量纲不统一，容易导致指标离散甚至矛盾，因此有必要综合各指标。Tang等[15]调查了1998—2017年中国4个城市道路相关数据，从设计、建设、运营、管理和创新方面建立分层贝叶斯网络模型，定性评价城市交通系统韧性。赵映璎等[16]从应急系统应对风险事故的承受能力、吸收能力、恢复能力、优化能力构建隧道施工应急系统韧性评价体系，采用可拓云模型综合评价系统韧性。黄亚江等[17]基于层次分析-粒子群优化算法和改进客观赋权法，从环境、人员、设备，以及管理4个方面构建地铁站火灾安全韧性综合评价模型。以上研究对象均未包括常发性拥堵下的城市地面交通系统。

通过相关文献分析，现有研究多以静态数据综合评价城市道路韧性，未考虑路网在“吸收-适应-恢复”过程的响应情况，无法凸显韧性的动态特性；且指标与韧性属性间缺乏对应关系，可解释性不强。部分研究指标相对单一，不符合韧性的多属性特征。本文的研究思路是将MFD与性能时序图相结合，提出考虑多个韧性属性的局部路网韧性评价指标，以反映局部路网在拥堵冲击下的整体响应过程，并采用CRITIC多属性决策组合赋权和模糊逻辑法分析局部路网韧性情况，最后实例验证所提出的方法的可行性。

1 韧性评价指标

本文从路网承载车流能力和车辆运行状态角度改进评价指标，明确指标针对性。改进指标对应于韧性的多属性特征，增强指标的可解释性。

1.1 基于宏观基本图的韧性指标

基于MFD的城市局部路网韧性评价指标，既不需要详细的网络模型，也不需要对不同的需求场景校准动态交通分配，利用图形展示交通流3要素之间的关系，并据此评价交通状态。图1的2条曲线分别对应信号配时优化前后的MFD曲线，通过优化提高路口通车效率，使交叉口在面临大流量冲击时维持较高的服务水平，进一步提高路网抵抗力。

图1 宏观基本图Fig.1 Macroscopic fundamental diagram

流量峰值差（difference of peak flows，DPF）。定义为优化前后局部路网内完成出行的流量差值。高峰时段车流量达到通行能力时，流量峰值越大路网冗余性越大，流量峰值差越大优化效果越明显。

式中：DPF为流量峰值差，pcu/（h·ln）；Qc，分别为优化后、优化前最大流量，pcu/（h·ln）。

临界密度差（difference of critical densities，DCD）。定义为优化前后局部路网的临界密度差值。高峰时段完成出行流量达到峰值时，临界密度越大说明车辆在整个路网中分布越均匀，间接反映资源丰富性越大。临界密度差越大则资源丰富性提升越大，利于提高路网达到拥堵状态的车容量。

式中：DCD为临界密度差，pcu/（km·ln）；kc，k'c分别为优化后、优化前的临界密度，pcu/（km·ln）。

1.2 基于性能时序图的韧性指标

性能时序图又被称为“韧性三角形”[12]，最早由Bruneau等[18]提出，是被广泛认可的韧性表征方式。图2横轴为时间，纵轴为性能指标P(t)。受到冲击时，时序曲线下降对应性能降低。冲击的种类和时长不同，会产生不同形态的时序曲线。

鲁棒性（robustness）、冗余性（redundancy）、资源丰富性（resourcefulness），以及快速性（rapidity）又称作韧性的4R属性。见图2，以RI代表鲁棒性，下降段斜率代表脆弱性，上升段斜率代表恢复快速性。鲁棒性是衡量局部路网抵抗冲击的能力，冗余性指路网的可替代资源，资源丰富性是冲击后可利用维修资源的数量，而快速性是充分利用资源并迅速恢复到原服务水平的能力。

图2 系统性能时序图Fig.2 Performance profile of the system

提出以路网加权平均速度作为性能测度P(t)是本文构建基于性能时序图的评价指标的基础，有助于管理者从宏观层面分析路网的运行效果。路网平均速度为

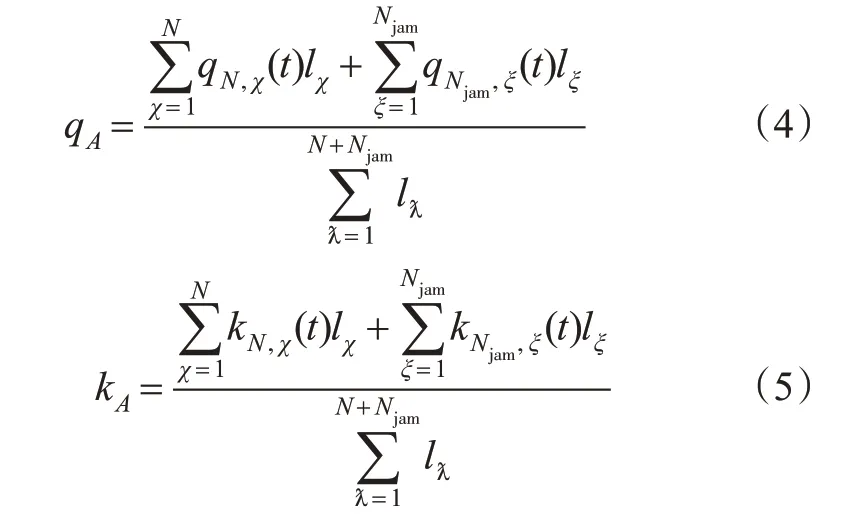
式中：ξ为常发性拥堵车道编号；χ为非常发性拥堵车道编号；lƛ为车道长度，km；N为非常发性拥堵车道数；Njam为常发性拥堵车道数；qA，qN，χ，qNjam，ξ分别为局部路网加权平均流量、非常发性拥堵车道流量与常发性拥堵车道流量，pcu/（h·ln）；kA，kN，χ，kNjam，ξ分别为局部路网加权平均密度、非常发性拥堵车道平均密度与常发性拥堵车道平均密度，pcu/（km·ln）。

鲁棒性指数（robustness index，RI）。定义为局部路网在平峰时段的平均速度P(t0)和大量车流冲击时平均速度最低点P(t)min之差，表征路网在受到冲击后性能下降的程度。同一干扰下鲁棒性指数越大，则受到冲击后的性能损失越大。

式中：RI为鲁棒性指数，km/h。

恢复快速性（rapid recovery，RR）。定义为局部路网平均速度从最低点到完成恢复的速率，其值为平均速度差与时间差之比。当恢复斜率≤0时性能持续下降，除非有外部支持作用，否则路网无法通过自修复回到原有水平。恢复曲线越陡峭，代表其快速性越好，自我愈合能力越强。

式中：RR为恢复快速性，km/h2；tl，te分别对应曲线最低点和恢复到原有水平的时刻，h。

损失面积比（ratio of loss areas，RLA）。定义为局部路网受冲击时的性能时序图下降面积与总面积之比。其值越大，表明干扰对路网性能的影响越大。

式中：RLA为损失面积比；ts为曲线下降起始时刻，h；P(ts)，P(te)为ts，te时刻对应的加权平均速度，km/h；P(t0)为局部路网维持在稳定水平时的性能值，km/h。根据RI、RR和RLA能描绘出完整的韧性三角形，为避免指标冗余，不引入降斜率。指标属性见表1。

表1 城市局部路网韧性评价指标Tab.1 Indexes to evaluate urban local road network resilience

2 局部路网韧性综合评价

交通领域综合评价有层次分析法[17]、贝叶斯网络法[15]、主成分分析法[19]等。其中，层次分析法和贝叶斯网络法都是以人的主观判断为前提；主成分分析法要保证提取的主成分累积贡献率达到较高水平，且主成分所反映的特征不一定清晰。模糊逻辑法则是将不确定信息转化为模糊概念，有利于对多个指标进行综合评价。考虑评价方法的实用性和客观性，本研究采用多属性决策组合赋权-模糊方法评价局部路网韧性。

2.1 基于CRITIC多属性决策组合赋权

为兼顾多指标数据的离散性、相关性和数据之间的可对比性，基于CRITIC准则的多属性决策组合赋权法计算指标权重[20]。

正向指标标准化处理，见式（9）。

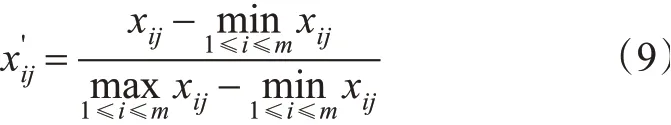
负向指标标准化处理，见式（10）。

式中：xij为评价方案i、指标j对应的值；为xij标准化结果。

以熵权法、变异系数法、因子分析3种方法计算各指标权重wς。Kendall一致性系数检验各赋权法结果是否具有一致性，若检验通过则表明各计算方式下的权重差异不大，以算数平均值为组合权系数。

未通过Kendall检验，说明权重间差异过大，不具协调性，以CRITIC的多属性决策最优组合赋权。

式中：W为组合权重向量；Mj为评价指标j包含的信息量；zyj为指标y和j之间的相关系数；σj为指标j的标准差；θς为组合权线性系数。

2.2 构建韧性综合评价模型

韧性反映了系统应对冲击的综合能力，单一指标如DPF、DCD、RI、RR、RLA分别只反映路网在性能下降、稳定和恢复阶段的部分特性。因此，本文提出以综合韧性得分衡量韧性全局响应。模糊综合评价是根据第i（i=1，2，…，m）个评价对象对于第j（j=1，2，…，n）个评价指标的样本值Xij，将第i个评价对象归入第uλ(x)（λ=1，2，…，l）个评语之中，以判断该因素隶属于评语u(x)的程度。最后将各评价对象隶属度向量组成隶属度矩阵，与韧性等级权重相乘得到综合评价得分。

1）数据序列矩阵。第i（i=1，2，…，m）个评价对象对于第j（j=1，2，…，n）个评价指标的样本值见式（15）。

2）隶属度函数。以分段函数作为隶属度函数，划分评语集u(x)={u1(x)，u2(x)，u3(x)，u4(x)}，分别对应极弱、弱、中等、较强，隶属度函数见式（16）～（19）。

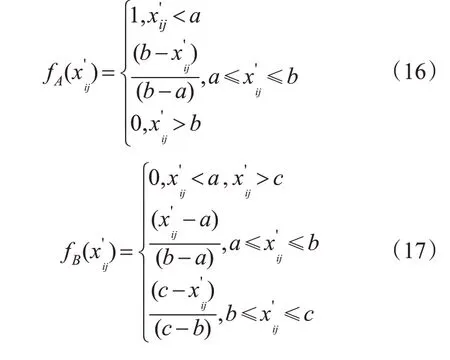
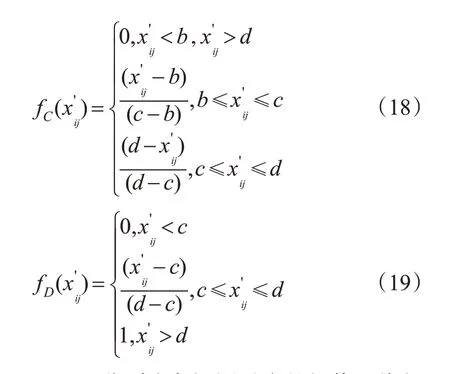
式中：a，b，c，d分别为各评语对应的阈值。将归一化指标通过绘制“累计频率曲线”划分阈值，其中各级别阈值分别为20%，40%，60%，80%[21]。

3）隶属度矩阵。由各评价指标j相对各评语的隶属度向量uj，组成隶属度矩阵U。

4）综合隶属度矩阵。指标权重向量W与隶属度矩阵U相乘得到综合评价矩阵B；对各评语进行赋值计算得到综合韧性得分r。

2.3 基于Likert的韧性分级

韧性分级可以辅助管理者针对不同韧性级别的局部路网采取相应的管控策略。基于Likert量表法[22]，分级取值范围见表2。

表2 韧性等级及取值范围Tab.2 Resilence levels and the value ranges

信号配时优化相当于对交叉口设备进行提升，进而增强路网抵抗大量车流冲击的能力。综上，为了验证提出的评价方法的有效性，对常发性拥堵路段进行排列组合，对组合中的常发性拥堵路段上的交叉口进行信号配时优化，然后采用Likert量表法对模糊评价下的韧性综合得分划分等级。

3 实例分析

3.1 局部路网概况

研究区域为长沙市商业圈五一大道周边路网，由湘江中路、五一大道、芙蓉中路及人民路围合的大约2 km2区域，包括29条路段ID和13个平面交叉口，见图3。该区域在晚高峰时段不但车流量大易发生拥堵，而且高峰时段持续时间较长，整体车流疏散速率缓慢，节假日拥堵更严重。

图3 研究区域Fig.3 Area for case study

3.2 交通数据采集

2021年4月20 日对研究区域内平面交叉口进行视频录像，通过视频观测记录高峰时段交叉口转向比例与信号配时；采用Python爬取高德交通态势数据（包括路段编号、道路角度、路况、速度、时间），根据道路交通条件对实际通行能力进行修正[23]，并将速度代入路阻函数反推交通流量。反推样本见表3。将反推流量与调查数据对比确保了反推结果的可靠性。

表3 基于互联网地图速度数据反推交通流量（样本2021-04-20 T18:51）Tab.3 Estimated traffic flows based on the speed data from the internet map（Sample 2021-04-20 T18:51）

式中：Cp，CB为单车道实际通行能力和基本通行能力，pcu/（h·ln）；αnum，αcross，αwidth，αother分别为车道修正系数、交叉口修正系数、车道宽修正系数、其他修正系数；v0，vd为路段修正自由流速度与路段设计车速，km/h；β1，β2，β3分别为自行车影响修正系数、车道宽度影响修正系数以及交叉口影响修正系数。

3.3 仿真数据准备

3.3.1 排列组合方案

为了对评价方法进行有效性验证，根据高德数据统计研究范围各路段1周内晚高峰时段拥堵频率并对其降序排列，对高频拥堵路段进行排列组合形成不同韧性改善路段方案。各方案本质区别即改善交叉口数量与位置不同。综合考虑拥堵频率与路网实际运营情况，确定该区域常发拥堵路段ID（拥堵频率）为：黄兴中路ID683（100%）、人民路ID-568（92.59%）、芙蓉中路ID-509（74.07%）、湘江中路ID492（62.96%）。选取每种韧性改善路段方案中的常发性拥堵路段上的交叉口，采取适用于队列到达（完全饱和流）的最短周期公式优化信号配时。

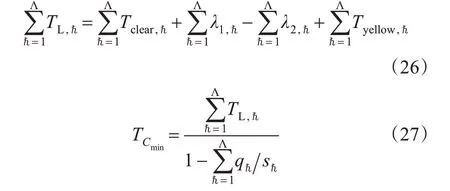
式中：TL，ℏ，Tclear，ℏ，λ1，ℏ，λ2，ℏ，Tyellow，ℏ为第ℏ个相位的信号损失时间、清空时间、启动延误时间、黄灯利用时间和黄灯时间，s；Λ为相位数；是第ℏ个相位的流量qℏ与饱和流率sℏ的比值；Tcmin为交叉口的最小信号周期时长，s。采用荷兰代尔夫特理工大学开发的信号设计软件VRIGen完成计算。

3.3.2 参数标定与场景设定

以晚高峰时段路网平均速度作为标定目标，通过方差分析法进行灵敏度分析，确定平均停顿距离、附加安全距离、多重安全距离、可见车数和期望速度五个标定目标。考虑到遗传算法具有标定精度高、不易陷入局部收敛的优点，以Python调用Vissim的COM接口，采用遗传算法标定模型。初始种群规模为10，交叉概率0.9，变异概率0.15，迭代次数10，当迭代到第5次后平均误差趋于稳定并小于3.5%。选择最优基因型0.004 5对应的参数组合作为最终标定结果，以保证仿真模型的有效性与研究结论的可靠性。

1）平峰时段模型。将平峰时段流量输入标定好的模型，设置仿真时长为36 000 s。

2）高峰时段模型。模拟路网流量在“平峰—高峰—平峰”的运行状态，流量逐级变化：0～3 600 s输入50%高峰时段流量，3 600～5 400 s输入75%高峰时段流量，5 400～12 600 s输入100%高峰时段流量，12 600～14 400 s输入75%高峰时段流量，14 400～36 000 s输入50%高峰时段流量。该模型信号配时与平峰时段模型一致。

3）信号优化模型。模拟路段排列组合的15种韧性改善路段方案在“平峰—高峰—平峰”的运行状态。流量和高峰时段模型均采取逐级输入。

3.3.3 仿真数据统计

为获取局部路网在各改善路段方案下的韧性评价指标，在Vissim模型上激活各路段的数据采集模块，选取采集时间戳、路段编号、车道编号、路段起终点坐标、通行流量和密度等数据；基于仿真输出的数据，采用式（4）和式（5）分别计算路网加权平均流量和加权平均密度，绘制路网MFD散点图；最后，采用最小二乘法对数据进行拟合得到kc与Qc，将优化前后临界密度做差得到DCD，将优化前后最大流量做差得DPF。求解式（3）得到路网平均速度并绘制速度时序图，对时序曲线采用式（6）～（8）计算得到RI、RR与RLA指标。

仿真运行的信号方案包括1个初始信号方案和对常发拥堵路段排列组合形成的15个方案，共构成16个方案。统计每个方案的评价指标，共得到16组数据。

4 结果讨论

4.1 数据分析与韧性分级

图4（a）是对方案12下编号为683，-568，-509的常发性拥堵路段上的交叉口进行信号配时优化，仿真得到局部路网MFD曲线。横坐标为车道数和长度加权的路网平均密度，纵坐标为车道数和长度加权的路网平均流量。圆圈散点为信号配时优化前路网的密度流量点，三角形散点代表对683，-568，-509这3条路段上交叉口进行信号配时优化后的密度流量点；实线是对圆圈散点拟合得到的MFD曲线，虚线是对三角形散点拟合得到的MFD曲线。信号配时优化后，行程时间减少从而产生了更高的平均流量525 pcu/（h·ln）＞492 pcu/（h·ln），利于增大局部路网容量，使其在相同流量冲击下降低拥堵程度。

图4（b）实线为方案12优化前局部路网平均速度时序曲线，虚线为优化后平均速度时序曲线。优化后路网平峰时段平均速度P(t)=31.052 km/h高于未优化P'(t)=28.730 km/h，说明原始信号配时未充分发挥路网通行能力，仍有一定的提升空间。优化后的曲线无明显下降段，RLA=0.037小于优化前RLA'=0.154，并且17：00—19：00的RI=0.816 km/h，小于优化前RI'=7.154 km/h。高峰时段低RI值说明路网抵抗冲击力强，具有较高抵抗外部冲击并维持原有服务水平的能力。值得注意，方案12的DCD为负，因为车辆分布的均衡性很大程度是由出行路径规划决定的。随着路况的改变，遵循原出行路径的车流通过信号配时优化路段的行程时间降低，从而引发韧性关键路段的转移。

图4 信号配时优化前后交通状况对比Fig.4 Comparison of the traffic conditions before and after signal timing improvement

通过Kendall一致性系数检验证明了各赋权法结果具有一致性。见表4，各指标权值排序为：鲁棒性指数RI＞损失面积比RLA＞恢复快速性RR＞临界密度差DCD＞流量峰值差DPF。鲁棒性指数RI、恢复快速性RR、损失面积比RLA权重占整体指标70.6%，三者影响韧性程度较大。负向指标对韧性起反作用，占比48.2%，正负指标相互制约，比重相当。

表4 指标权重及级别阈值Tab.4 Weights of indexes and their thresholds of grades

将各情况下的MFD曲线与性能时序曲线进行平滑处理，计算韧性评价指标见表5。表5中每行对应1个方案：对该方案“优化路段ID”上的交叉口信号配时优化，仿真后提取路网中所有路段（含非常发性拥堵路段与常发性拥堵路段）的流量、速度等参数，根据第1节所提出的公式计算得到局部路网在该信号配时方案下的韧性指标。在相同的流量冲击下，方案8，10，16的RI和RLA均＜0.001，说明这几种方案能有效吸收大量冲击，路网性能无明显下降。

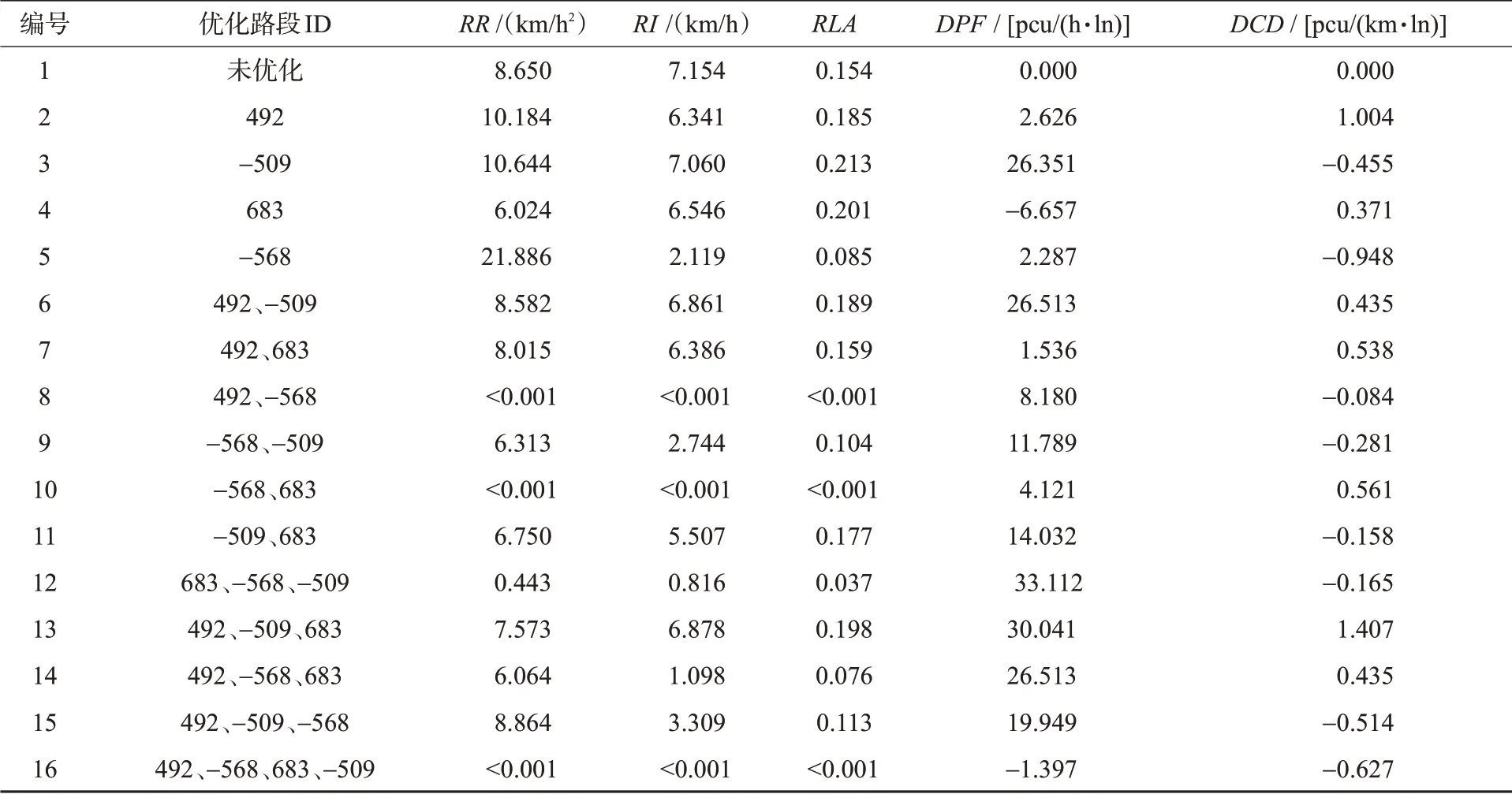
表5 不同排列组合方案下路网的韧性指标Tab.5 Indexes of the road network resilience with different permutations and combination schemes

根据Likert量表法对韧性分级，见表6随着优化路段数的增加，综合韧性得分呈上升趋势。未优化路网得分51，优化1，2，3条拥堵路段的路网韧性平均分为55，61，67。4条路段均优化的韧性得分59。

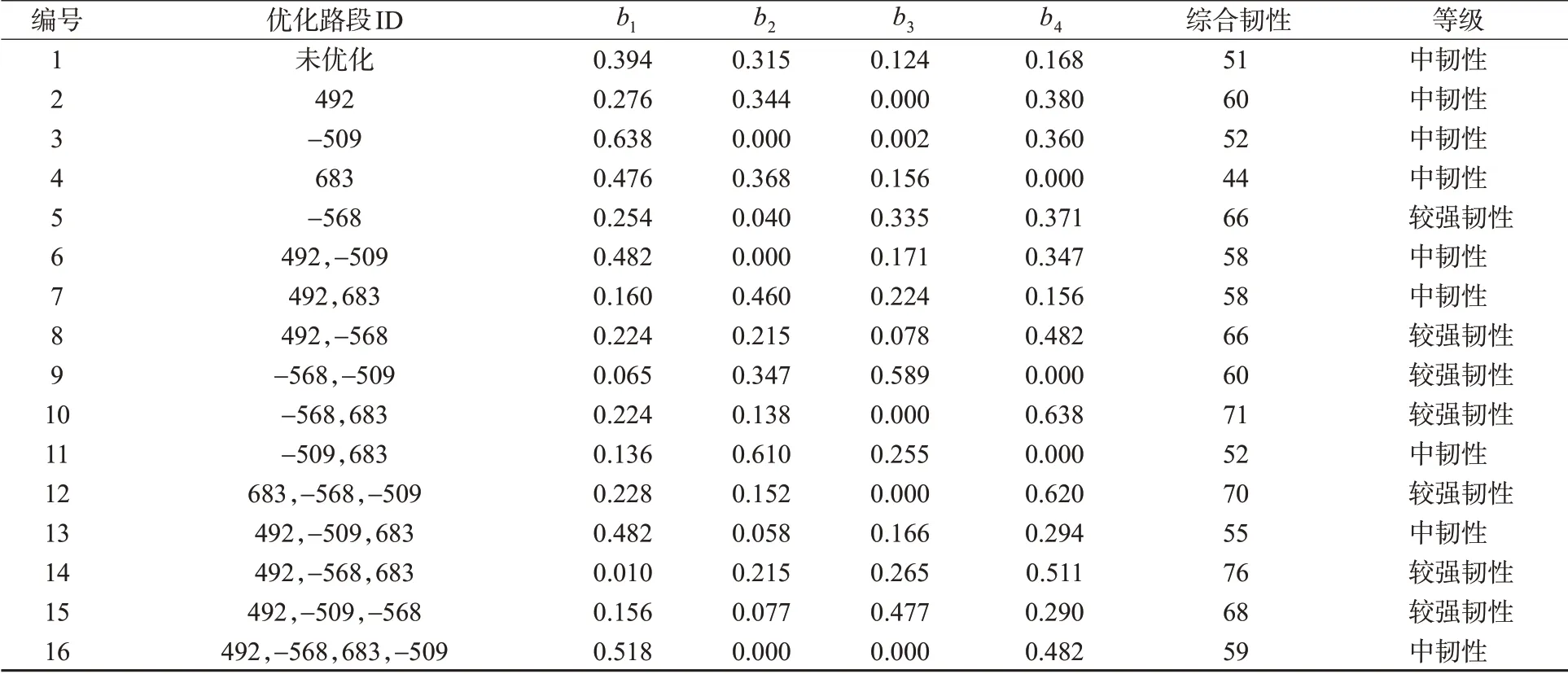
表6 路网综合韧性评分与等级划分Tab.6 Comprehensive resilience scores and classifications of the road network resilience

分析各方案综合评分，相同改善路段数中综合评分最高的方案均包含同一路段ID，可见此路段是常发拥堵路段中，对于路网韧性具有重要影响的路段。优化常发性拥堵路段数相同时，优化效果与交叉口位置有明显相关关系。在单条拥堵路段优化中，路段ID-568得分最高66。在2条和3条拥堵路段优化中，综合韧性值最高的方案10和方案14均包含路段-568，说明该路段对路网韧性有明显影响。在同等流量冲击下，方案14的评价分数在所有方案中最高。本文方法能区分不同状态的局部路网韧性，具有一般适用性。综合韧性得分具有随着优化路段数的增加而增长的趋势，但不是线性递增。信号配时优化导致路网韧性特性发生变化，部分影响城市局部路网韧性的路段发生转移。因此单纯增加优化数量不是最优策略。单条路段优化时，中、较强韧性占比75.0%，25.0%；双路段优化时中、较强韧性占比50.0%，50.0%；3条路段优化时，中、较强韧性占比25.0%，75.0%；4条路径均优化仅为较强韧性，验证了前文所提出韧性关键路段转移的观点。常发拥堵路段需要依据具体路网区域与交通状况的变化进行识别和变更。

4.2 评价方法对比

为验证提出的方法对评价局部路网韧性的有效性，采用文献[13]提出的MVI指标与文献[18]提出的韧性损失指标R对案例进行评价。将优化后路网类比于MVI指标中的正常路网，未改善路网类比于事件路网。以综合得分最低方案4和最高方案14进行评价方法的对比，结果发现：方案4和方案14在MVI评价下排名为12和8，在R评价下排名为15和5。其规律为：MVI与DPF更相似，其值越大方案排名更靠前；R与RLA更相似，其值越大方案排名越靠后。

分析排名存在差异的原因：MVI是将不饱和、饱和、过饱和区域内所有密度值下正常路网平均速度与事件路网下平均速度之比求和，并除以事件路网下的密度最大值，仅考虑了路网平均速度在MFD中的几何关系。R仅考虑恢复到事件前100%水平的损失能量累积。不同于强调系统抵抗干扰的鲁棒性以及强调恢复阶段的快速，韧性更强调系统吸收、协调适应与恢复的全局动态响应过程，因此本文所提出的评价指标综合考虑了MFD与性能时序图的几何特征，充分反映鲁棒性、冗余性、资源丰富性和快速性的韧性4R属性。

5 结束语

本文关注城市局部路网韧性的衡量指标与综合评价，梳理国内外文献发现：韧性评价指标零散，综合评价多基于较易获取的大范围数据与专家，缺乏对城市路网常发性拥堵韧性的评价。研究提出将MFD与性能时序图相结合的路网韧性综合评价方法，贡献主要有以下几方面。

1）提出考虑常发性拥堵的城市局部路网韧性的评价指标。将MFD与4R属性相结合，设计了鲁棒性指数、损失面积比、恢复快速性、临界密度差与流量峰值差5个指标。运用多属性决策组合赋权确定各指标对大量车流冲击的响应程度依次为：鲁棒性指数RI＞损失面积比RLA＞恢复快速性RR＞临界密度差DCD＞流量峰值差DPF。

2）验证了文章提出的考虑常发性拥堵的城市局部路网韧性综合评价方法的有效性。选择长沙市商业圈局部路网为研究对象，将常发性拥堵路段进行排列组合，对各组合内常发性拥堵路段上的交叉口进行信号配时优化；运用VISSIM建立路网原始信号配时和优化方案的仿真模型，获得不同MFD与时序图，并结合结果图阐述了指标的计算步骤。研究结果表明该方法对不同路况韧性计算的适应性，丰富了路网韧性的评价方法。

3）将本文所提出的评价方法与文献中已有评价指标进行对比，评价结果存在共性与差异。相比于已有的研究，本研究综合考虑更多反映路网韧性属性的指标，具有合理性与全面性。

实际工作可以用从已经安装在道路基础设施中的车辆检测器采集实时交通数据，计算指标以衡量道路网络的性能，对处于低韧性路网上的常发性拥堵路段及时采取信号配时优化，引导车辆运行，提高局部路网韧性。本研究仅考虑了对常发性拥堵路段上的交叉口进行信号配时优化时，路网韧性的评价方法。未来研究将关注以下方面：①多交叉口协调控制或边界控制对路网韧性的影响；②建立实时识别动态交通状况的管理平台，及时掌握影响路网韧性的拥堵路段和进行相应的交叉口信号配时优化。