岩体动态渗透对引水隧洞稳定性的影响分析

郭 翔，高 飞

（水发规划设计有限公司，济南 250000）

由于我国水资源时空分布不均匀， 为满足中西部生活和工业用水需求， 我国在中西部地区大量建设引水隧洞工程。 但中西部地区的地形复杂和地质特殊， 时常出现影响引水隧洞安全的工程灾害，例如隧洞开挖时遇到的高外水压力、高地应力，以及引水隧洞充水前、 后引起的衬砌和围岩变形等问题，对引水隧洞建设提出巨大挑战。

近年来，国内外学者研究表明，水力耦合作用下的隧洞稳定性是引水隧洞工程安全建设的关键因素。 对引水隧洞的渗流-应力耦合分析也获得众多研究成果。陈卫忠等［1］基于深埋引水隧洞工程实例， 研究管道围岩和衬砌渗透压力的分布规律并探究运营期间衬砌的受力特征。吴世勇等［2］为评估渗流场增量变化对隧洞的稳定性和支护结构的影响，对某深埋引水隧洞工程展开现场试验，分析渗流增加对隧洞衬砌位移和应力分布情况的影响。王克忠等［3］基于有限元软件，构建隧洞数值模型，模拟隧洞开挖时受渗流影响应力重分布趋势和演变规律。

在隧洞开挖时， 若多孔介质岩体无法承受岩体应力和孔隙水压力的变化，将会导致岩体渗透率、孔隙度等性质改变，从而引起隧洞内衬结构变形，产生裂隙破坏； 而隧洞内衬结构的改变进一步加剧岩体结构的应力应变规律的转变， 引起隧洞产生弹塑性工程问题。与此同时，国内外学者认为隧洞变形和应变能直观的反映出岩体受力产生破坏的过程， 因此国内外学者相继开展研究。

刘仲秋等［4］基于某地区引水隧洞工程，探究引水隧洞内衬结构变形和岩体裂隙受渗透系数影响下的演变规律，并结合等效饱和多孔介质原理，探究围岩与衬砌结构应力-渗流耦合规律。 周亚峰等［5］提出等效渗透系数， 并对引水隧洞全过程建设进行数值分析，量化渗透系数受结构变形演变规律。 马荣富等［6］为分析隧洞变形、 渗透系数和孔隙率的对应函数关系，结合Biot固结原理，对隧洞裂隙水力耦合展开数值模拟。

综上所知， 国内外学者已探究出渗流对引水隧洞建设的影响规律并对变形演化方式展开了详细的研究。但目前引水隧洞水力耦合全过程分析，尤其是岩体达到塑性屈服后的水力相互耦合仍有待进一步探讨。故本文基于有限元软件，通过数值仿真技术模拟饱和岩体水力完全耦合作用，探究岩体应变、孔隙率和渗透系数对应函数关系， 并评估动态渗透性对引水隧洞的稳定性影响。

1 渗透性演化模型设定

1.1 饱和岩体渗透性原理

基于工程实际，传统渗流力学忽视了饱和岩体孔隙度、渗流率的演化规律，从而导致数值与工程实际存在偏差，故本文基于岩体物性参数，构建动态演化数值模型。 基于冉启全、李士伦的研究成果和渗流力学Kozeny方程［9］，若εv<0，即岩体达到扩容阶段，推导出孔隙度ϕ和渗透系数k可表示为：

同时，图1显示了孔隙度φ-体积应变εv对应关系曲线，孔隙度φ与体积应变εv其呈线性关系（当孔隙度φ为正值时，呈正线性相关；当孔隙度φ为负值时，呈负线性相关；以纵轴为线，对称分布）。同理，图2显示了渗透系数k-体积应变εv对应关系曲线， 体积应变εv与渗透系数k呈对称分布关系曲线。

图1 孔隙率与体积应变的关系曲线

图2 渗透系数与体积应变的关系曲线

1.2 模型参数设定

以某地区引水隧洞为参照，隧洞尺寸如图4。 隧洞断面为马蹄形型式， 其内部衬砌为厚60cm 的C25钢-混结构，施工过程采用全封闭支护。 两隧洞间距为47m净岩体，约等于隧洞洞径的3.6倍。为更好地模拟岩体动态渗透对引水隧洞稳定性的影响，设定模型尺寸为460×640m，模型顶部和底部距离地表分别为1600和1830m，隧道设定环境为地下水位线以下，隧道岩体达到饱和状态。 模型顶部设定自重等效应力44.8MPa， 两侧孔隙水压力为梯形分布，如图5。

图3 孔隙率与体积应变的关系曲线

图4 渗透系数与体积应变的关系曲线

表1 材料基本力学基本性质

2 数值模拟结果及分析

2.1 围岩渗透系数演化规律及位移验证

图5显示引水隧洞拱顶与拱底处渗流系数演变规律。从图中可看出，隧洞开挖边界处的渗透系数变化较大，拱顶处渗透系数为3.3×10-6m/s；拱底处渗透系数为1.0×10-6m/s，而后随距离的递增，渗透系数逐渐降低，拱顶的降幅区间最大。符合隧洞实际开挖时监测应力和渗透系数变化趋势。

图5 围岩渗透系数分布

为研究岩体渗透系数的影响，本文设置两种工况进行对比（工况1为渗透系数定值模型，工况2为基于体积应变的渗透动态演化模型），图6和图7分别为隧洞拱顶和隧洞右侧拱腰处位移监测。 对比数据可知，隧洞位移均随距离的递增而递减，且工程实际监测值均处于两种模拟工况之间， 说明数值仿真结果具有一定的合理性。 同时，相比采用定值渗透系数的工况1的数据，采用动态渗流演化渗透系数的工况2的数据更大，符合工程安全实际的需求。

图6 拱顶往围岩深处位移分布对比

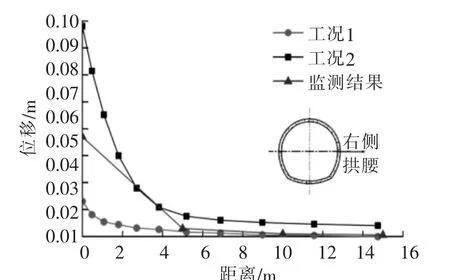
图7 拱腰往围岩深处位移分布对比

2.2 渗透性演化对隧洞稳定性影响分析

图8为引水隧洞拱顶处深处充水后孔隙水压力对比曲线，工况1和2的演变规律呈现差异性。 工况2在拱顶洞距离3m左右， 孔隙水压力出现局部下降，然后缓慢增长的趋势； 而工况1则呈现一种递增发展趋势。 图9为引水隧洞拱顶处深处排水后孔隙水压力对比曲线，工况1和2总体呈现增幅趋势，孔隙水压力随距离的递增而增加。 但工况2在拱顶3m范围内孔隙水压力出现小幅度缓慢降低，而后呈现递增趋势。

图8 充水后拱顶沿围岩深处孔隙水压力对比

图9 排水后拱顶沿围岩深处孔隙水压力对比

2.3 隧洞拱顶和拱底处变形分析

图10和图11分别为拱顶、 拱底处计算步-位移对比关系。 隧洞拱顶处充水后，压力得到集中，导致位移出现局部下降，排水后压力缓和，位移局部上升；相对而言隧洞拱底处，一直承受压力，故充水和排水具有相同的增幅趋势。 拱底位移均随计算步的增加而增加。 同时，从图中也可看出，图10和图11均显示，无论是拱底位移还是拱顶位移，工况2的值均大于工况1的值。 隧洞拱顶处，工况2位移值比工况1位移值的多大约100%；隧洞拱底处，工况2位移值要比工况1位移值多近200%。 而检测数据基本呈现相同的趋势，均位移两种工况之间，说明数值仿真模型较好的模拟工程实际， 而工况2值较大是由于考虑引水隧洞附近渗透系数变化的影响，从而导致隧洞岩体位移增大，仿真数据结果符合工程监测数据的变化趋势［7］。

图10 拱顶处计算步-位移对应关系

图11 拱底处计算步-位移对应关系

图12和图13分别为引水隧洞拱顶和拱底处岩体计算步-塑性应变对比关系。 从图中可知，引水隧洞在两种工况下， 岩体塑性应变均随着计算步的增加而递增。 但增幅趋势呈现差异性，在隧洞拱顶处，工况1塑性应变随计算步的增加增幅不显著， 而工况2在计算步为4时出现较为明显的增加； 在隧洞拱底处，工况1和2均随计算步的增加，塑性应变产生缓慢增加趋势［8］。

图12 拱顶处计算步-塑性应变对比关系

图13 拱底处计算步-塑性应变对比关系

图14为衬砌处计算步-拉应力对应关系。从图中可知，工况1和工况2下，衬砌处拉应力均随计算步的增加而增加，但工况2的增幅值要大于工况1；计算步由3到第4步时， 工况1和工况2分别增幅约11%和35%。 这一阶段，两种拉应力值增幅相差较大，在工程实际中，应重视对该工序的加固和监测。

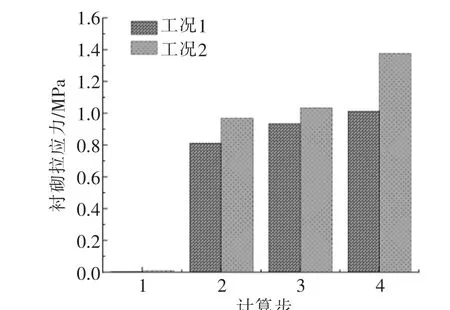
图14 衬砌处计算步-拉应力对应关系

3 结语

（1）结合多孔介质有效应力原理，构建有限元岩体动态渗透演化模型， 对岩体在水力渗流作用下受荷过程进行数值模拟，并与现场监测数据进行对比，发现不同工况下计算结果和现场数据具有相似性，说明计算模型具有较好的精确性和可靠性。

（2）为探究引水隧洞充水前后的变化，将渗透系数设为定值及采用动态渗流演化模型两种工况。 系数为定值时，其孔隙水压力趋于定值，而采用动态渗流演化模型其孔隙水压力值起伏较大， 且充水前后情况对比， 发现充水后拱顶变形和拱底位移数值要比充水前工况下分别增加近100%和200%。

（3）采用动态渗流演化模型比将渗透系数视为定值的仿真结果更接近工程实际， 且发现当渗透系数为定值时，从充水到排水工况下，隧洞衬砌拉力峰值增幅约11%， 而数值模型显示其拉力峰值增幅约35%，两者差值较大，在隧洞施工过程中对其应着重监测。