非局部守恒Allen-Cahn方程的高效算子分裂格式

崔晨， 吴哲， 翟术英

(华侨大学 数学科学学院， 福建 泉州 362021)

1 预备知识

近年来，带有非局部算子的Allen-Cahn方程等相场模型引起了广泛的关注，且在数学、物理、力学、图像处理和材料科学等领域得到了成功的应用. 例如，相变[1]、近场动力学理论[2]、图像修复[3]和非局部热传导[4]. 由于经典的Allen-Cahn方程不保持其初始质量，Rubinstein等[5]提出了一个守恒型的Allen-Cahn方程，这个问题与相变的扩散界面模型有密切的关系；随后他们的模型在文献[6]中得到了广泛的分析和数值研究.

文中，考虑如下带有周期边界条件的非局部Allen-Cahn方程，即

(1)

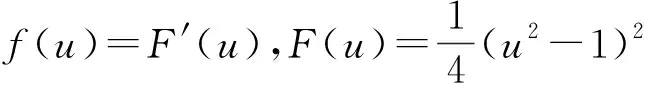
(2)

式(2)中：卷积核J满足ⅰ)J(x)≥0，∀x∈Ω；ⅱ)J(x-y)=J(y-x)；ⅲ) J是Ω周期的.

非局部Allen-Cahn方程(1)可以看作能量泛函的L2梯度流[8]，即

(3)

对能量泛函E(u)关于时间t求导，可得

(4)

由上述推导可知，能量泛函E(u)是非增的.

与经典Allen-Cahn方程[9-12]的大量研究相比， 非局部Allen-Cahn方程的数值结果较少.额外的非局部项给开发快速有效的算法带来了巨大的数值挑战，因此许多学者致力于这一方面的研究.Du等[13]研究了非局部Allen-Cahn问题的傅里叶谱逼近；Zhai等[14-15]结合谱方法和解析法，研究了分数阶非局部Allen-Cahn模型的快速显式算子分裂方法；Weng等[16]对此方法进行进一步推广，并给出了误差分析；Liu等[17]研究了几类非局部和分数阶模型的数值分析及快速算法；Guan等[18]研究了非局部Allen-Cahn和Cahn-Hilliard方程的二阶凸分裂格式，且利用非线性多重网格方法求解离散产生的非线性方程；Tian等[19]对非局部扩散方程的不同逼近形式做了比较并给出理论分析.

鉴于此，本文给出求解守恒型非局部Allen-Cahn方程的数值格式及质量守恒定理，并通过两个数值算例验证算法的有效性.

2 数值格式

2.1 非局部算子的离散格式

首先，从文献[20]关于非局部算子Lδ的分析，可将算子Lδ转化为卷积形式.对于任意函数u(x，t)，有

Lδu(x，t)=(J*1)u(x，t)-J*u(x，t).

(5)

于是，可将Lδu在点(xi，tm)，(0≤i≤N，0≤m≤M)处离散为

(6)

(7)

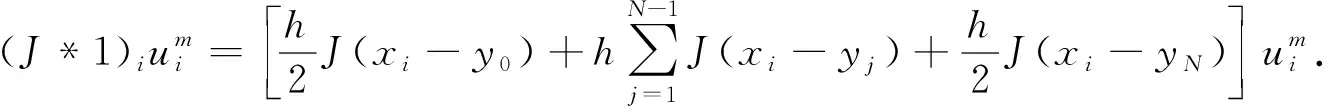
(8)

因此，针对任意的N+1阶向量u=(u0,u1,…,uN-1,uN)T， 有

Lδu=-h×

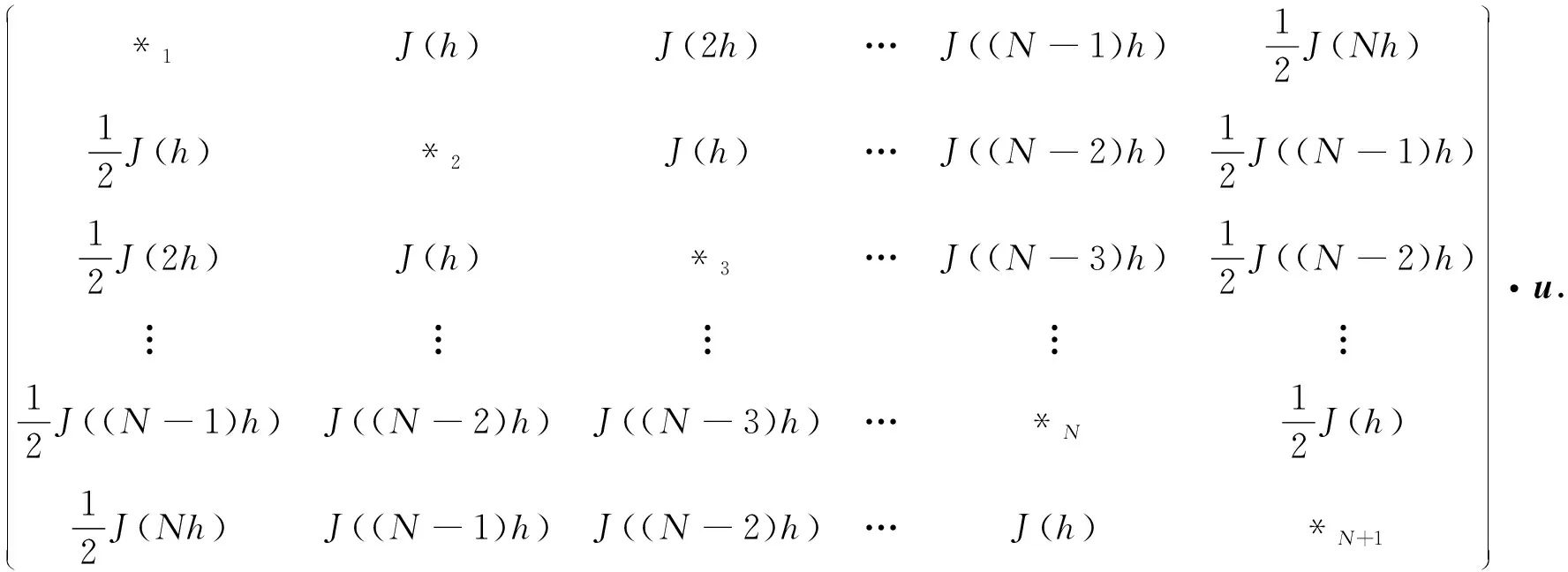
(9)

式(9)中：*i的值为所在行其余值和的相反数.

2.2 算子分裂法求解非局部Allen-Cahn方程

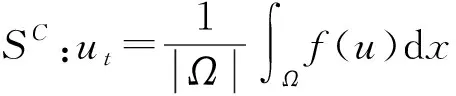
u(t+τ)=SA(t)SB(t)SC(t)u(t)+O(τ).

(10)

式(10)中：非线性方程解析求解，非局部方程利用C-N格式求解，拉格朗日乘子方程利用数值积分求解，从而得到简单高效的数值格式.

非线性方程SA可通过解析式得到， 即

(11)

式(11)中：um表示第m层数值解.

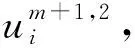
(12)

对上述等式进行整理，并写成矩阵形式有

(13)

式(13)中：I表示单位矩阵.

拉格朗日乘子方程SC可通过数值积分离散为

(14)

(15)

(16)

将式(16)代入式(14)，可得

(17)

结合等式(11)，(13)，(17)， 可获得算子分裂格式为

(18)

证明：方程(18)的第3个式子与e=(1,1,…，1)T作内积，并对i求和，可得

(19)

3 数值算例

通过数值算例来验证理论分析的正确性，包括数值格式的收敛性、能量稳定性、质量守恒等. 所有的算例均选择空间区域Ω=[-1，1]，高斯核J由下列等式给出[20]，即

(20)

3.1 算例1

取初值u0(x)=0.1cos(2πx)，x∈[-1，1].为验证空间收敛阶，将时间剖分固定为M=3000.计算当ε=0.1，δ=0.5，T=1时，不同N值的空间收敛阶， 如表1所示.由表1可知： 随着网格剖分变细，E2及E∞变得越来越小， 且收敛精度逐渐接近预期的二阶收敛.

表1 空间收敛阶(ε=0.1，δ=0.5，T=1，M=3 000)Tab.1 Spatial convergence order of different schemes (ε=0.1，δ=0.5，T=1，M=3 000)

将空间剖分固定为N=3000， 计算当ε=0.1，δ=0.50，T=1时，不同M值的时间收敛阶， 如表2所示.由表2可知：随着网格剖分变细，E2与E∞均变得越来越小， 且此方法在时间上达到一阶精度.

表2 时间收敛阶(ε=0.1，δ=0.50，T=1，N=3 000)Tab.2 Spatial convergence order of different schemes (ε=0.1，δ=0.5，T=1，N=3 000)

3.2 算例2

将能量函数E(u)进行离散，可得

(21)

取初值u0(x)=0.2sin(πx)cos(πx)，x∈[-1，1]， 其相应的参数为ε=0.1，T=200，N=500，M=1 000.分别取δ=0.10，0.20，0.21，0.30，得到不同δ值的数值解、能量变化及质量图像，分别如图1～2所示.

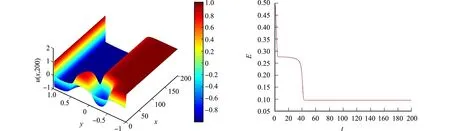
(a) 数值解(δ=0.10) (b) 能量变化(δ=0.10)

(c) 数值解(δ=0.20) (d) 能量变化(δ=0.20)

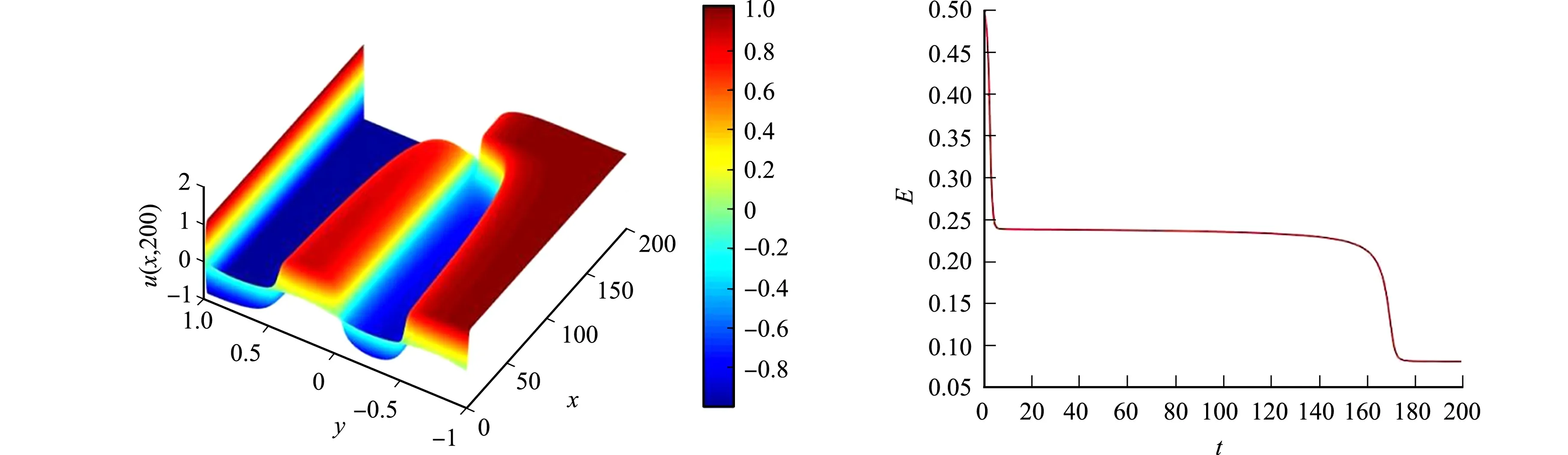
(e) 数值解(δ=0.21) (f) 能量变化(δ=0.21)

(g) 数值解(δ=0.30) (h) 能量变化(δ=0.30)图1 算例2不同δ值的数值解和能量变化图Fig.1 Numerical solution and energy change diagram of different δ values of example 2

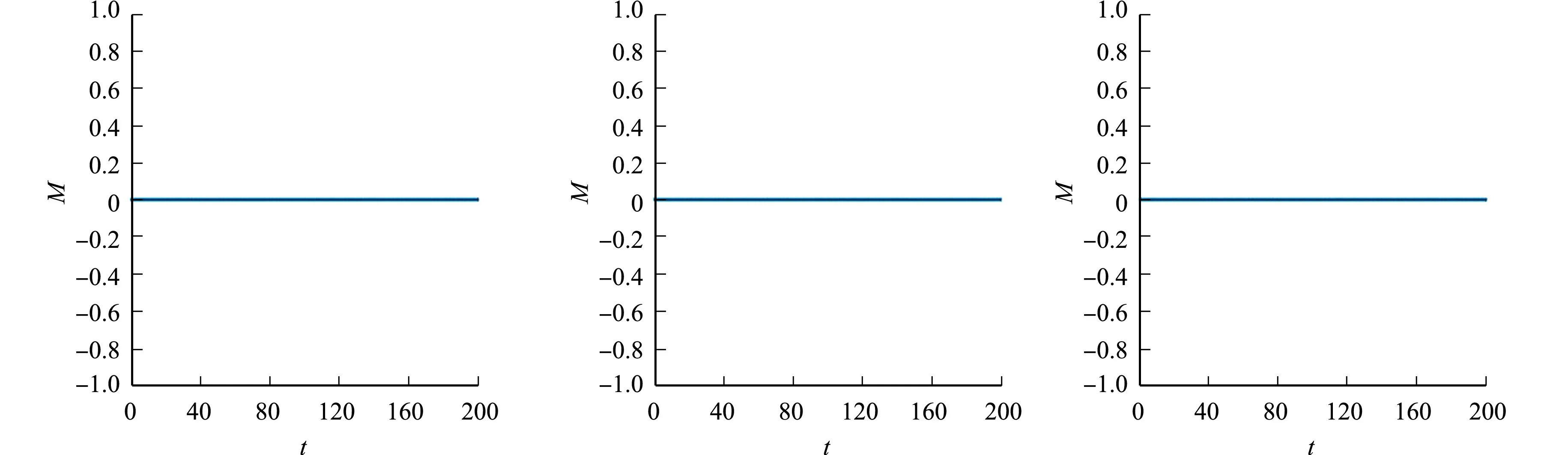
(a) δ=0.10 (b) δ=0.20 (c) δ=0.30图2 算例2不同δ值的质量图Fig.2 Quality map of different δ values of example 2

由图1可知:能量函数E(u)随着时间t的增加而减小，满足能量递减规律，且能量耗散与δ的大小有关，δ越大， 方程达到稳态所需时间越长.从图2可知：对于不同δ值，所给出格式均满足质量守恒的性质.

4 结束语

文中研究了守恒型非局部Allen-Cahn方程. 首先利用算子分裂方法将原方程分解为3个子问题，并构造相应数值求解格式.理论分析表明，格式满足质量守恒. 最后，通过数值算例验证了所给格式的有效性.