预制CFRP筋增强条加固素石板受弯性能有限元分析
2022-09-15陈志新苗伟叶勇
陈志新, 苗伟, 叶勇,2
(1. 华侨大学 土木工程学院, 福建 厦门 361021; 2. 华侨大学 福建省结构工程与防灾重点实验室, 福建 厦门 361021)
石材是人类最早使用并沿用至今的建筑材料之一,具有抗压强度高、耐久性能好、取材方便等特点.在我国东南沿海地区,目前仍有大量的石结构民居建筑在役,构成独特的区域建筑特色[1].在这部分石结构建筑中,主要的结构构件包括承重墙、柱、梁、板等,均由当地出产的天然石材制作而成.天然石材属于脆性材料,且抗拉强度远小于其抗压强度,故石梁、石板这类石结构受弯构件的变形能力较弱,如不采取必要的增强措施则容易出现脆性破坏.为提高石结构建筑在正常使用和意外作用下的安全性,在尽可能保护建筑特色的前提下对石梁、石板进行加固十分重要.另一方面,石材是我国部分地区的重要产业,在不影响外观的前提下提高石材制品的开裂性能,对于扩大石材产业的应用范围具有显著意义.
碳纤维增强复合材料( carbon fiber reinforced polymer,CFRP)具有轻质高强、耐腐蚀、抗疲劳性好等特点,近年来在结构加固领域得到越来越多的关注和应用[2].武晓敏等[3]对4根未加固石梁和4根CFRP加固石梁试件进行受弯性能试验,研究CFRP对改善石梁承载能力和破坏形态的作用.Wei等[4]对CFRP加固石材构件的受弯性能进行研究,结果表明,采用CFRP布进行加固可提高石梁的受弯性能,破坏形态由脆性破坏转变为具有一定变形能力的破坏.戴泉玉[5]的研究结果表明,CFRP布能有效提高石梁的承载力和变形能力.Fayala等[6]研究不同层数玻璃纤维增强复合材料(GFRP)条带加固石砌体梁的效果,并通过数值模型分析加固后石砌体梁的破坏形态和承载力.Shrive[7]的研究结果表明,纤维增强复合材料(FRP)可提高石结构构件的抗裂性,从而有效增强石结构的整体性.郭子雄等[8]进行了26个花岗岩石材表层嵌埋CFRP筋试件的拔出试验,研究CFRP筋直径、锚固长度和粘结材料厚度对石材-CFRP筋粘结性能的影响.刘阳等[9]基于表层嵌埋加固法,提出在石梁受拉区开槽并嵌埋CFRP筋的组合石梁技术.Ye等[10-11]将表层嵌埋预应力CFRP筋技术与石结构受弯构件结合,提出表层嵌埋预应力CFRP筋组合石梁/板,并通过试验研究这一组合结构构件的力学性能.文献[12-14]采用预制CFRP筋增强板、增强条分别对石梁、石板进行加固,并开展了试验研究,结果表明,预制CFRP筋增强板、增强条可显著提高石板的承载力和变形性能.
上述的石结构受弯构件加固技术中,预制CFRP筋增强板/条加固技术具有现场操作简便、加固效果良好等特点,且对石结构受弯构件原有外观的影响较小,可用于对既有石结构尤其是历史风貌石结构进行加固.与此同时,目前的研究仅停留在模型试验阶段,对于加固机理和定量化效果仍有待进一步深入探讨.为此,本文采用通用非线性有限元程序对预制CFRP筋增强条加固石板的受弯性能进行建模,开展了参数分析,研究不同参数对加固石板受力性能的影响规律,并提出对应的承载力计算模型.
1 有限元模型
1.1 已有试验的试件参数
有限元分析模型参照文献[13]中的6个预制CFRP筋增强条加固素石板试件,试件参数,如表1所示.表1中:br为增强条的横截面宽度;Db,n,ρ分别为CFRP筋的直径、数量和配筋率.石板的长×宽×高为2 000 mm×300 mm×60 mm,试验段长度为1 800 mm.预制CFRP筋增强条的长度与被加固石板相同,均为25 mm;增强条的宽度有50,70 mm两种,每块增强条内嵌1根CFRP筋,CFRP筋的直径有5,7 mm两种;CFRP筋配筋率为0.10%~0.19%.

表1 试件参数Tab.1 Parameters of specimens
1.2 有限元模型
预制CFRP筋增强条加固石板有限元模型,如图1所示.采用有限元程序ABAQUS进行预制CFRP筋增强条加固石板受弯性能的有限元建模分析,有限元模型的几何参数与实际试件相同.文献[13]的研究表明,所用的粘结剂可有效粘结CFRP筋、增强条与被加固石板,加载试验过程中未发现各部件间的滑移现象.因此,采用ABAQUS软件中自带的嵌埋功能将CFRP筋嵌在粘结剂中,忽略CFRP筋与粘结剂之间的相对滑移;粘结剂与石板之间采用绑定定义其接触行为,假定两者的变形完全同步.

图1 预制CFRP筋增强条加固石板有限元模型Fig.1 Finite element model of slab strengthened with prefabricated CFRP-reinforced stone strips
1.3 有限元单元选取与网格划分
有限元模型中,石板、增强条与粘结剂采用三维减缩积分实体单元(C3D8R)进行模拟,CFRP筋则采用三维桁架单元(T3D2)进行模拟.为提高有限元计算的收敛性,采用结构化网格划分技术对所建立的有限元模型进行网格划分,其中,所有部件的网格尺寸均设置为20 mm左右.
1.4 边界条件与荷载施加方法
为模拟实际试验中4点弯曲加载的边界条件,将有限元模型的一端设置为固定铰支座,即约束所有平动自由度和除平面之外的转动自由度,另一端设置为滑动铰支座,即约束除石板长度方向之外的平动自由度和除平面之外的转动自由度.设置参考点,并将加载面耦合至参考点进行位移加载,最大加载位移为60 mm.
1.5 材料本构关系模型
材料本构关系模型,如图2所示.图2中:εtu,εcu为石材极限受拉应变、受压应变;σs,εs分别为石材应力、应变;fst,fsc分别为石材抗拉强度、抗压强度;σf,εf分别为CFRP筋的受拉应力、受拉应变;σfu,εfu分别为CFRP筋极限受拉应力、受拉应变;σw,εw分别为粘结剂的受拉应力、受拉应变;σwu,εwu分别为粘结剂极限受拉应力、受拉应变.

(a) 石材 (b) CFRP筋 (c) 粘结剂图2 材料本构关系模型Fig.2 Material constitutive relation models
石材与混凝土的材性相近,具有受压强度高和容易开裂等特性.采用ABAQUS软件中的混凝土损伤塑性模型模拟石材,石材的受压应力(σc)-受压应变(εc)关系采用文献[15]提出的模型(图2(a)).该模型将石材受压分为上升和下降两个过程,上升阶段呈线性,石材的峰值受压应变(ε0)取为3 000×10-6,极限受压应变(εcu)取为3 300×10-6.石材单轴受压模型表达式为
σc=Esεc,εc≤ε0(上升阶段),
(1)

(2)
石材单轴受拉模型表达式为
σt=Esεt,εt≤fst/Es(破坏前),
(3)
σt=0,εt>fst/Es(破坏后).
(4)
式(1)~(4)中:Es为石材弹性模量;ξ=εc/ε0;σt,εt分别为石材受拉应力、受拉应变.
定义CFRP筋为线弹性材料,其应力(σf)-应变(εf)关系,如图2(b)所示.CFRP筋模型表达式为
σf=Efεf.
(5)
式(5)中:Ef为CFRP筋的弹性模量.
定义粘结剂近似为线弹性材料,其应力(σw)-应变(εw)关系,如图2(c)所示.粘结剂模型表达式为
σw=Ewεw.
(6)
式(6)中:Ew为粘结剂的弹性模量.
2 数值模型验证及分析
2.1 破坏模式
有限元计算得到的石板应力分布与试验破坏模式的对比,如图3所示.由图3可知:素石板试件P-1最终在纯弯段出现一条裂缝并突然发生断裂破坏,试件破坏前变形不明显,一裂即断,为典型的脆性破坏;其他预制CFRP筋增强条加固石板试件在弯曲加载过程中均产生多条裂缝,挠曲变形明显,破坏模式从脆性断裂转变为弯曲破坏,且破坏前的挠曲变形明显.在加固石板试件中,有限元模拟和试验得到的开裂截面受压区高度接近.总体而言,有限元模拟得到的石板变形、破坏形态与试验结果相近.

(a) 试件P-1

(b) 试件S-1d5-50

(d) 试件S-1d5-70

(e) 试件S-1d7-70

(f) 试件S-2d5-300图3 有限元计算得到的石板应力分布与试验破坏模式的对比Fig.3 Comparison between stress distribution of slabs calculated by finite element method and experimental failure modes
2.2 荷载-挠度曲线
试件的荷载(P)-挠度(Δ)曲线的有限元模拟结果和试验结果对比,如图4所示.由图4可知:有限元模拟结果和试验结果总体吻合较好.其中,有限元模拟和试验得到的初始刚度接近,试件开裂时对应的荷载和挠度基本一致.除素石板试件P-1和CFRP筋配置较少的试件S-1d5-50外,有限元模拟和试验均获得了加固石板明显的裂缝开展阶段和类强化阶段.

(a) 试件P-1 (b) 试件S-1d5-50 (c) 试件S-1d5-70

(d) 试件S-1d7-70 (e) 试件S-2d5-50 (f) 试件S-2d5-300Fig.4 荷载-挠度曲线的有限元模拟结果和试验结果对比Fig.4 Comparison of load-deflection curves between finite element simulated results and experimental results
此外,石板开裂后的荷载-挠度曲线均呈现锯齿形波动,对应新裂缝的产生及受拉区石材退出工作.有限元模拟得到的曲线波动幅度小于试验结果,主要原因在于有限元模型基于连续体假设,石板开裂时模型并未真正断开,故荷载的下降幅度较小.
2.3 加固石板截面高度-跨中应变曲线
加固石板截面高度(h)-跨中应变(εs)曲线的有限元模拟结果和试验结果对比,如图5所示.图5中:Pcr为开裂荷载.由图5可知:石板开裂前,跨中应变沿截面高度基本呈线性分布,中性轴位于截面高度中部.由于加固石板的受拉弹性模量(Et)略小于其受压弹性模量(Ec),中性轴随荷载的增大逐渐上移,且随着荷载增大,加固石板受拉区逐渐产生细小裂缝,受拉弹性模量(Et)进一步降低.

(a) 试件P-1 (b) 试件S-1d7-70 (c) 试件S-2d5-300Fig.5 加固石板截面高度-跨中应变曲线的有限元模拟结果和试验结果对比Fig.5 Comparison of height-midspan strain curves of strengthened stone slabs between finite element simulation results and experimental results
2.4 CFRP筋应变
荷载-跨中位置CFRP筋应变有限元模拟结果与试验结果对比,如图6所示.由图6可知:当荷载小于石板的开裂荷载时,有限元模拟得到的曲线与试验曲线较吻合;石板开裂后,两者略有差异,但整体趋势基本吻合.由于试验中部分试件的CFRP筋应变计过早发生破坏,使有限元模拟得到的CFRP筋应变最大值大于试验结果.

(a) 试件S-1d7-70 (b) 试件S-1d5-70 (c) 试件S-2d5-50Fig.6 CFRP筋应变有限元模拟结果和试验结果对比Fig.6 Comparison of CFRP bar strain between finite element simulation results and experimental results
2.5 典型荷载-挠度曲线
预制CFRP筋增强条加固石板的典型荷载-挠度曲线,如图7所示.图7中:A,B,C点分别对应试件达到开裂荷载、进入类强化、达到极限荷载的时刻.由图7可知:预制CFRP筋增强条加固石板的荷载-挠度曲线呈现典型的三阶段发展趋势,第1阶段为开裂前的弹性阶段,此阶段荷载主要由石材承担,荷载与挠度呈线性发展关系,到达开裂荷载时,试件开裂,荷载突然下降;第2阶段为裂缝开展阶段,随着荷载增大,试件跨中挠度增大,加固石板沿纯弯段范围内出现多条裂缝,荷载-挠度曲线呈锯齿状发展;第3阶段为类强化阶段,纯弯段的裂缝充分发展后,受拉区石材退出工作,拉力完全由CFRP筋承担,随着CFRP筋应力增大,荷载呈上升趋势,直至加载结束.不同点(A,B,C)状态对应的应力云图,如图8所示.
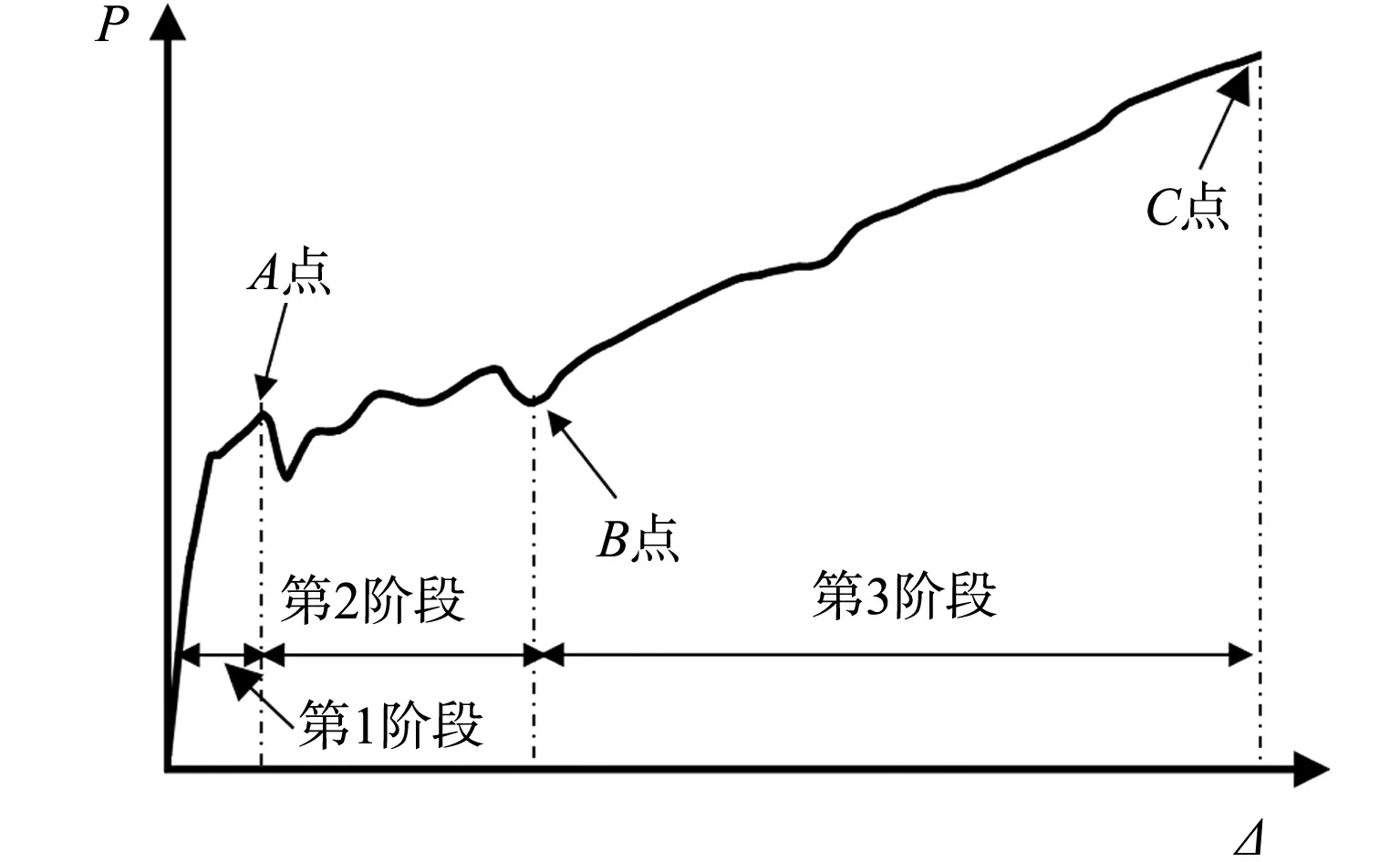
图7 典型荷载-挠度曲线Fig.7 Typical load-deflection curve

(a) A点状态

(b) B点状态

(c) C点状态图8 不同点状态对应的应力云图Fig.8 Stress nephograms corresponding to different point states
3 参数分析
3.1 有限元模型参数
由上述内容分析可知,有限元模型可较准确地模拟预制CFRP筋增强条加固石板的受弯力学性能.基于文中建立的有限元模型,研究不同CFRP筋直径、CFRP筋配筋率、增强条宽度及厚度(cr)对加固石板受力性能的影响.有限元模型参数,如表2所示.

表2 有限元模型参数Tab.2 Parameters of finite element model
3.2 不同参数对承载力的影响
有限元模拟得到的不同参数对加固石板荷载-挠度曲线的影响,如图9所示.由图9(a),(b)可知:随着CFRP筋直径和配筋率的增大,加固石板的极限承载力均有明显提高,由于开裂前荷载主要由石材承担,石板的开裂荷载较为接近;此外,CRPP筋用量的增加使石板开裂后筋材产生的应变增量减小,故试件的荷载-挠度曲线主要呈两阶段形式,曲线的锯齿状波动较少.由图9(c),(d)可知:加固石板的开裂荷载和极限荷载均随增强条厚度和宽度的增大而提高,且曲线呈三阶段发展形式.
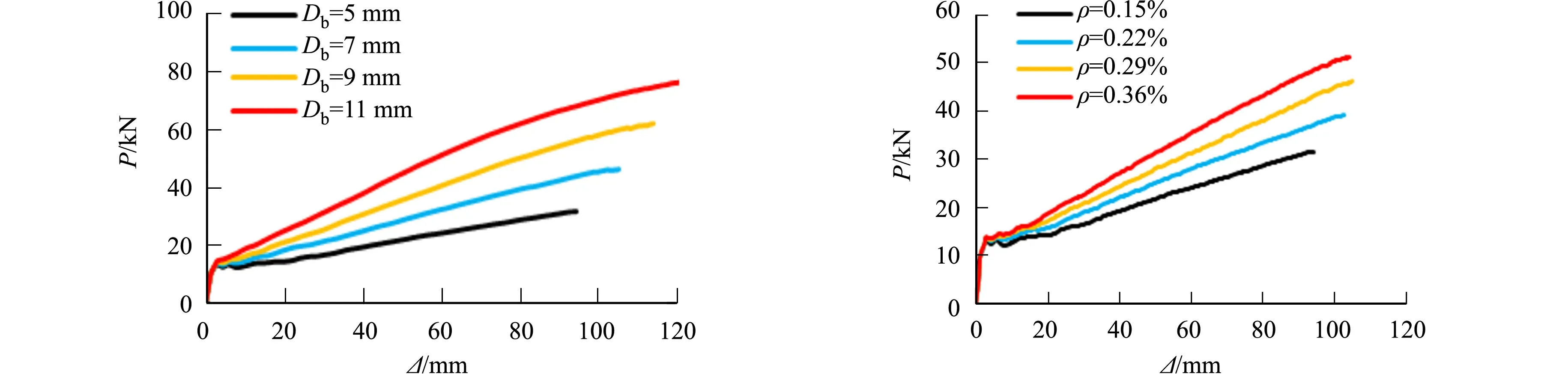
(a) CFRP筋直径 (b) CFRP筋配筋率

(c) 增强条厚度 (d) 增强条宽度图9 不同参数对加固石板荷载-挠度曲线的影响Fig.9 Influence of different parameters on the load-deflection curves of strengthened stone slabs
3.3 开裂荷载
受力过程中,当受拉区石材达到其抗拉强度时,石板发生开裂.对于素石板,其截面惯性矩全部由素石板提供.对于加固石板,考虑到试件中CFRP筋的截面与素石板和增强条相比较小,故忽略CFRP筋,只考虑增强条对被加固石板抗弯截面惯性矩的增大作用.故石板的开裂弯矩(Mcr)为
Mcr=Izfst/αtyc.
(7)
式(7)中:fst=10.0 MPa;Iz为截面惯性矩;αt为折减系数;yc为受拉区石材边缘至中性轴的距离.
当增强条宽度较小时,需要考虑折减系数.折减系数αt根据增强条宽度与石板宽度(b)的比值确定:当br≤b/3时,αt取0.90;当b/3
开裂弯矩计算值(Mcr,c)与有限元模拟值(Mcr,FEA)的对比,如表3所示.由表3可知:公式计算结果与有限元模拟结果总体吻合良好,Mcr,c/Mcr,FEA的平均值为0.99,均方差为0.001.

表3 开裂弯矩计算值与有限元模拟值的对比Tab.3 Comparison between calculated values and finite element simulation values of cracking bending moment
3.4 极限承载力
对于采用预制CFRP筋增强条加固的石板而言,可能产生两种破坏状态,即受压区石材边缘压溃或受拉区CFRP筋达到极限应变而断裂.由于石材抗压强度较高,考虑CFRP筋达到极限应变而发生断裂破坏.根据截面受力平衡条件,可得
Fsc-Ff=0.
(8)

根据截面变形协调关系,可得
(9)
式(9)中:εstc为石材受压边缘应变,εstc=σstc/Es;h0为石材受压边缘至CFRP筋的距离.
由式(8)可得
(10)
根据受力平衡,得到加固石板的极限弯矩(Mpf)为
(11)
极限弯矩计算值(Mpf,c)与有限元模拟值(Mpf,FEA)的对比,如表4所示.由表4可知:公式计算结果与有限元模拟结果总体吻合良好,Mpf,c/Mpf,FEA的平均值为0.99,均方差为0.010.

表4 极限弯矩计算值与有限元模拟值的对比Tab.4 Comparison between calculated values and finite element simulation values of ultimate bending moment
4 结论
1) 建立的有限元模型得出的荷载-应变曲线和破坏形态均符合试验结果,表明文中建立的有限元模型适用于模拟分析预制CFRP筋增强条加固石板的受力情况.
2) 全过程受力分析发现,试件最初由石板承受拉力,达到开裂荷载时,试件的承载力下降,产生较多的裂缝;随着荷载的逐渐增大,增强条的受拉应力逐渐变小;由CFRP筋受拉,CFRP筋应变逐渐增大.预制CFRP筋增强条加固石板在一定程度上能提高试件的开裂荷载和极限荷载.
3) 参数分析发现,CFRP筋的直径和配筋率、增强条的宽度和厚度会影响石板的承载能力.CFRP筋的直径和配筋率对试件的开裂荷载影响不大,但是会对极限承载力造成影响;增强条的宽度和厚度对试件的开裂荷载具有较大的影响,但对极限承载力影响不大.
4) 提出的计算模型符合试验结果,对比计算模型和有限元模型的计算结果可知,提出的计算模型能够较好地分析预制CFRP筋增强条加固石板的开裂荷载、破坏形态及试件的抗弯承载力.
